Đề thi thử Toán TSA (Đề 24) | Đại học Bách Khoa Hà Nội

40 Đề TSA | Phạm Tú Khanh
Ngày:___/___/_____. Điểm: ___/40.
Đề Thi Thử Đánh Giá Tư Duy Toán Học.
Câu 1. [Mức 1] Tại một công viên nước, giá một vé người lớn đắt hơn
VNĐ so với giá của một
vé trẻ em. Vào một buổi chiều cuối tuần, số vé trẻ em bán được nhiều hơn số vé người lớn chiếc và
công viên nước kiếm được tổng cộng
VNĐ. Nếu hoán đổi giá vé của trẻ em và người lớn thì
công viên đã có thể kiếm được bao nhiêu tiền từ buổi chiều hôm đó? A. VNĐ. C. VNĐ. B. VNĐ. D. VNĐ.
Câu 2. [Mức 1] Bất phương trình có tập nghiệm là ? A. . C. . B. . D. .
Câu 3. [Mức 1] Tập nghiệm của bất phương trình chứa bao nhiêu số nguyên dương? ➢ Điền đáp án: .
Câu 4. [Mức 1] Ký hiệu
nhằm chỉ đạo hàm của hàm số theo ẩn . Chẳng hạn: .
Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Sai Đúng a. . ○ ○ b. . ○ ○ c. Nếu thì . ○ ○ d. Nếu thì . ○ ○
Câu 5. [Mức 1] Cho hàm số
. Những mệnh đề nào sau đây đúng? (Chọn nhiều đáp án)
A. Tập giá trị của hàm số trên là . B. Trên , hàm số có tập giá trị là . C. Trên , đồ thị hàm số
cắt trục hoành tại điểm phân biệt. D. Trên , đồ thị hàm số
cắt trục hoành tại điểm phân biệt.
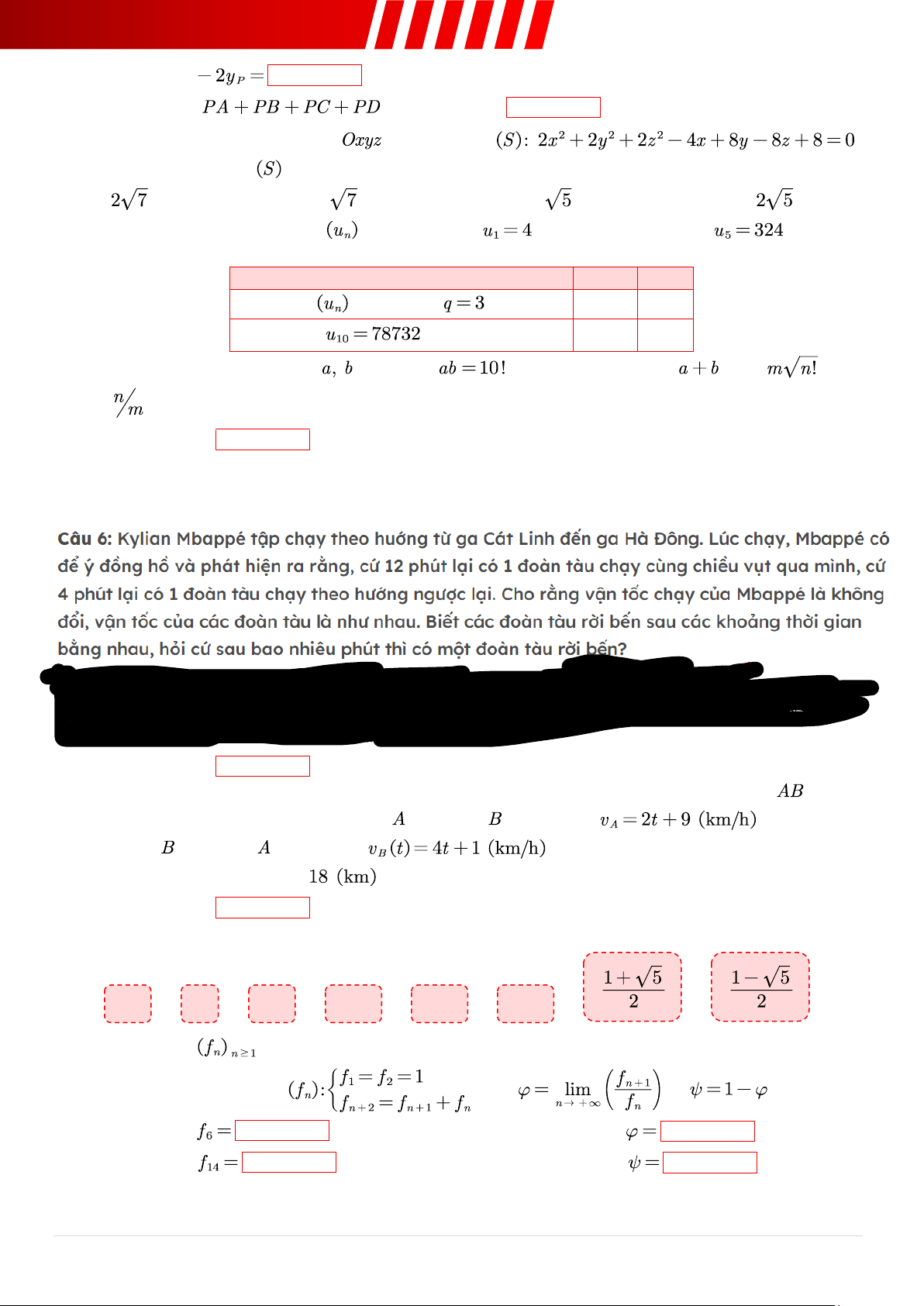
Câu 6. [Mức 1] Điền số nguyên thích hợp vào chỗ trống. Trong hệ trục toạ độ , cho bốn điểm và và một điểm có toạ độ sao cho tổng đổ dài
đạt giá trị nhỏ nhất. a. Giá trị của .
40 Đề TSA | Phạm Tú Khanh b. Giá trị của . c. Tổng độ dài nhỏ nhất bằng .
Câu 7. [Mức 1] Trong không gian , cho mặt cầu .
Đường kính của mặt cầu bằng? A. . B. . C. . D. .
Câu 8. [Mức 2] Cho cấp số nhân có số hạng đầu
và số hạng thứ năm là . Xét tính
đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Dãy số có công sai . ○ ○ b. Số hạng . ○ ○
Câu 9. [Mức 2] Cho hai số thực thoả mãn
, giá trị nhỏ nhất của bằng . Giá trị của bằng? ➢ Điền đáp án: .
Câu 10. [Mức 2] Trong mặt phẳng, 20 đường tròn có thể cắt nhau tại tối đa bao nhiêu điểm phân biệt? A. 190. B. 380. C. 400. D. 200.
Câu 11. [Mức 3] Một màn hình cỡ lớn trong rạp chiếu phim cao và đặt ở độ cao
so với mặt sàn. Biết rằng
góc nhìn của người xem là
, hàng ghế 1 cách màn hình
, chiều cao mắt người xem ở hàng ghế 1 đến mép dưới màn hình bằng
, khoảng cách ngang giữa hai hàng ghế liên tiếp bằng
và hàng ghế sau cao hơn hàng ghế trước đó
(tham khảo hình vẽ bên). Nên lựa chọn hàng ghế nào xa màn hình nhất để đảm
bảo góc nhìn của người xem tối thiểu bằng ? ➢ Điền đáp án: .
Câu 12. [Mức 2] Hai ô tô xuất phát tại cùng một thời điểm trên cùng một đoạn đường dài 50
(km). Ô tô thứ nhất bắt đầu xuất phát từ và đi đến với vận tốc ; ô tô thứ hai
xuất phát từ và đi đến với vận tốc
. Sau bao lâu, tính từ thời điểm hai ô tô
xuất phát, thì chúng cách nhau ? ➢ Điền đáp án: .
Câu 13. [Mức 2] Kéo và thả các phương án thích hợp vào chỗ trống. 13 8 21 144 377 233 Dãy số Fibonacci
, được phát minh bởi nhà toán học Leonardo Bonacci, là một dãy số tự nhiên
thoả mãn công thức truy hồi . Đặt và . a. Giá trị của . c. Giá trị của . b. Giá trị của . d. Giá trị của .
40 Đề TSA | Phạm Tú Khanh
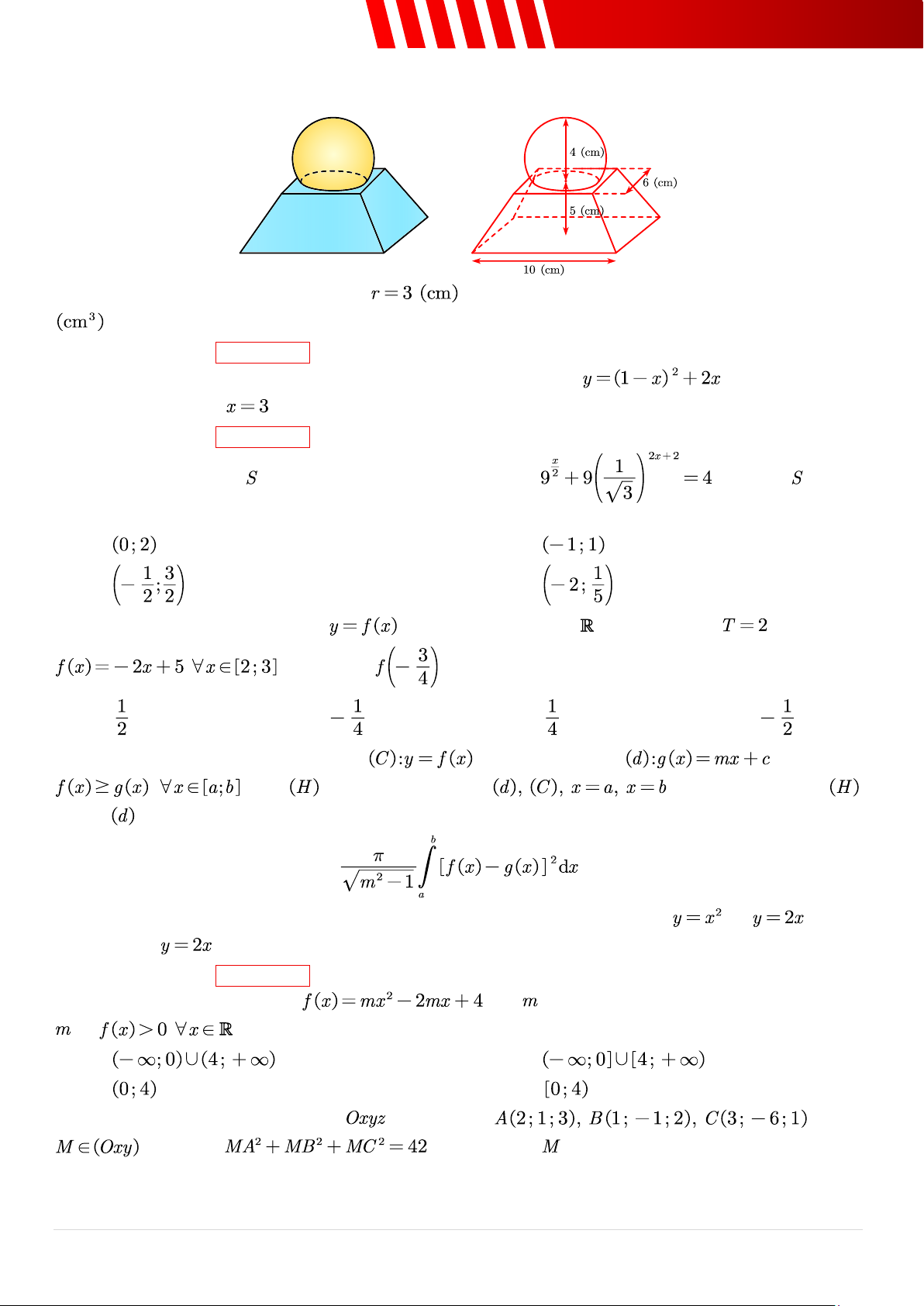
Câu 14. [Mức 3] Một món đồ lưu niệm bằng thuỷ tinh có phần dưới là một khối chóp cụt và phần
trên là một phần của khối cầu với các kích thước như hình vẽ sau:
Biết rằng khối cầu ban đầu có bán kính
, thể tích của món đồ lưu niệm này bằng bao nhiêu
? (Làm tròn kết quả đến hàng phần trăm) ➢ Điền đáp án: .
Câu 15. [Mức 1] Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành, trục tung và đường thẳng bằng? ➢ Điền đáp án: .
Câu 16. [Mức 1] Gọi là tổng nghiệm của phương trình . Khi đó, có thể
thuộc những khoảng nào sau đây? (Chọn nhiều đáp án) A. . C. . B. . D. .
Câu 17. [Mức 1] Cho hàm số chẵn, xác định trên và có chu kỳ . Biết rằng , giá trị của bằng? A. . B. . C. . D. .
Câu 18. [Mức 1] Cho đường cong và đường thẳng thoả mãn . Gọi
là miền giới hạn bởi . Thể tích khi quay quanh
được xác định bởi công thức:
Khi đó, thể tích của vật tạo được khi quay miền giới hạn bởi đồ thị hàm số và quanh đường thẳng
bằng? (Làm tròn kết quả đến hàng phần chục)1,5 ➢ Điền đáp án: .
Câu 19. [Mức 1] Cho hàm số
, với là tham số thực. Tập hợp các giá trị của để là? A. . C. . B. . D. .
Câu 20. [Mức 3] Trong không gian , cho ba điểm . Điểm thoả mãn . Cao độ điểm bằng? A. 0. B. 1. C. 2. D. 3.
40 Đề TSA | Phạm Tú Khanh
Câu 21. [Mức 3] Cho hai số thực dương thoả mãn . Giá trị
nhỏ nhất của biểu thức là? ➢ Điền đáp án: .
Câu 22. [Mức 1] Chọn ngẫu nhiên số từ tập
. Xác suất để tổng hai số
được chọn là một số lẻ là? A. . B. . C. . D. .
Câu 23. [Mức 3] Hình vẽ bên mô tả một bề mặt được tạo bởi
hai hình chữ nhật có độ dài , ,
với phần giao được ghép với một mặt trụ có trục qua và song song với , bán kính đáy và
. Một con sên đã bò trên bề mặt từ đến và để
lại một đường dấu vết đằng sau (đường nét đứt). Xét tính
đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Độ dài cung bằng . ○ ○
b. Từ hình trên, con sên đã chọn con đường ngắn nhất. ○ ○
c. Quãng đường ngắn mà con sên có thể đi là ○ ○ .
Câu 24. [Mức 2] Điền số nguyên thích hợp vào chỗ trống.
Một hộp đựng 8 quả cầu trắng, 12 quả cầu đen. Lần thứ nhất lấy ngẫu nhiên 1 quả cầu trong hộp, lần
thứ hai lấy ngẫu nhiên 1 quả cầu trong các quả cầu còn lại.
a. Không gian mẫu của phép thử trên bằng .
b. Xác suất để hai lần lấy được 2 quả cầu cùng màu là , giá trị của bằng .
Câu 25. [Mức 2] Cho hàm số . Biết rằng , giá trị của bằng? ➢ Điền đáp án: .
Câu 26. [Mức 1] Kéo và thả các phương án thích hợp vào chỗ trống. Cho hàm số và
có đồ thị như hình vẽ bên.
Dựa vào đồ thị, ta có: .
Câu 27. [Mức 2] Điền số nguyên thích hợp vào chỗ trống. Trong không gian , cho hai điểm .
là điểm thuộc tia đối của tia sao cho . Toạ độ của là .
40 Đề TSA | Phạm Tú Khanh
Câu 28. [Mức 2] Số điểm biểu diễn nghiệm của
trên vòng tròn lượng giác là? A. 3. B. 4. C. 5. D. 6.
Câu 29. [Mức 2] Số nguyên tố bé nhất thoả mãn
là lập phương của một số chẵn là? ➢ Điền đáp án: .
Câu 30. [Mức 2] Cho hình chóp có cạnh bên
vuông góc với đáy là tam giác đều cạnh ,
. Khoảng cách giữa hai đường thẳng và bằng? A. . B. . C. . D. .
Câu 31. [Mức 2] Số nghiệm nguyên của bất phương trình là? A. 10. B. 5. C. 7. D. 8.
Câu 32. [Mức 2] Cho hai hàm số và
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a. Đạo hàm . ○ ○ b. là một hàm số chẵn. ○ ○
c. Tổng các nghiệm của phương trình ○ ○
là một số chia hết cho 2025.
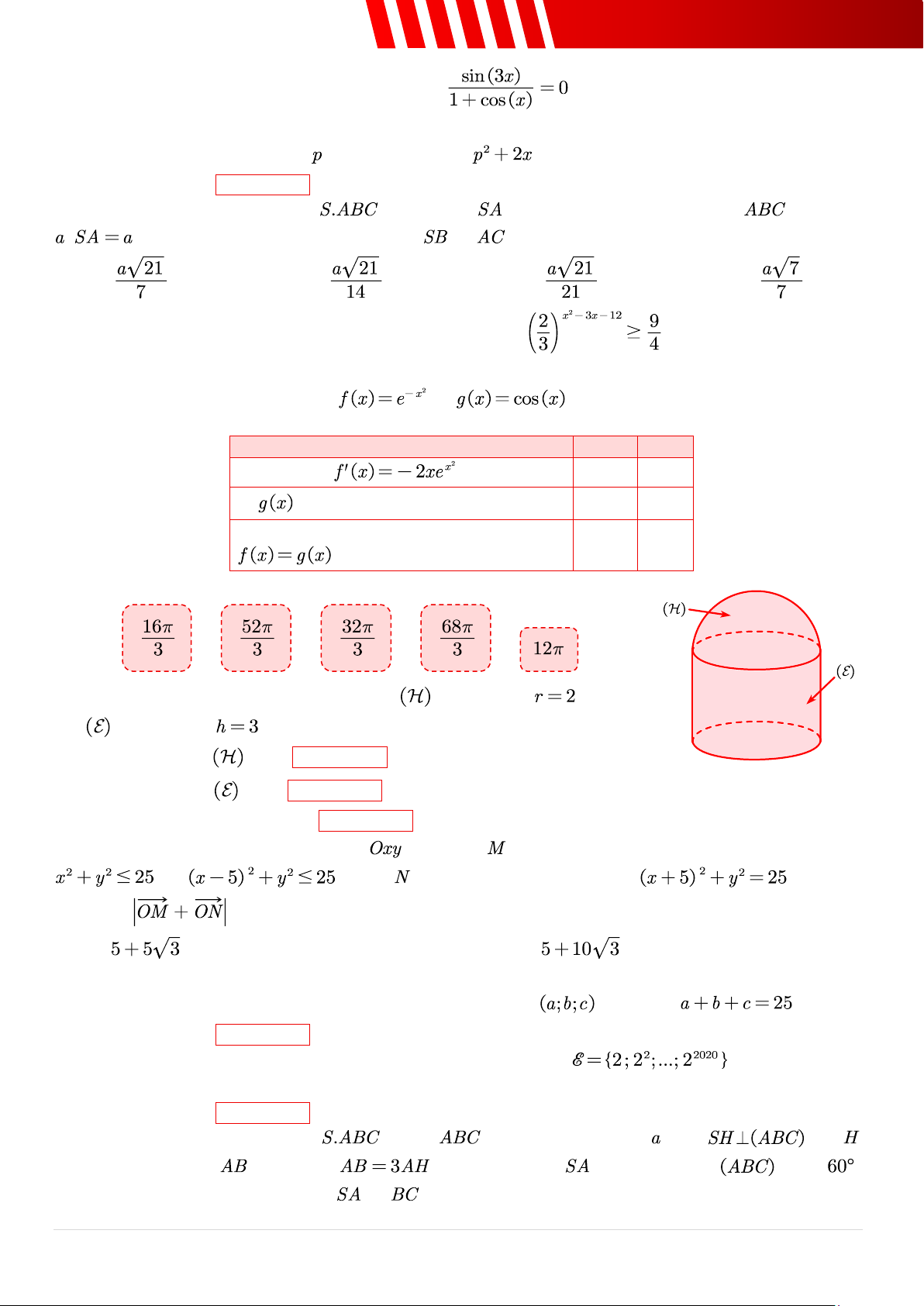
Câu 33. [Mức 2] Kéo và thả các phương án thích hợp vào chỗ trống.
Một món đồ được làm ra một nửa quả cầu có bán kính với hình trụ có chiều cao (như hình vẽ bên). a. Thể tích của bằng . b. Thể tích của bằng .
c. Thể tích của món đồ bằng .
Câu 34. [Mức 3] Trong hệ trục toạ độ , cho điểm
linh động trong miền giao giữa hai hình tròn và , điểm
linh động trên đường tròn . Giá lớn nhất của bằng? A. . C. . B. 10. D. 5.
Câu 35. [Mức 3] Tồn tại bao nhiêu cặp số nguyên dương lẻ thoả mãn ? ➢ Điền đáp án: .
Câu 36. [Mức 3] Có bao nhiêu tập con có ba phần tử thuộc tập sao cho ba phần
tử đó lập thành một cấp số nhân? ➢ Điền đáp án: .
Câu 37. [Mức 3] Cho hình chóp có đáy
là tam giác đều cạnh . Biết , với là điểm thuộc cạnh thoả mãn , và góc tạo bởi và mặt phẳng bằng .
Khoảng cách giữa hai đường thẳng và bằng?
40 Đề TSA | Phạm Tú Khanh A. . B. . C. . D. .
Câu 38. [Mức 3] Cho phương trình , với . Biết rằng phương
trình đã cho có nghiệm khi và chỉ khi tích . Giá trị của bằng ? ➢ Điền đáp án: .
Câu 39. [Mức 3] Cho dãy số
. Xét tính đúng/sai của các mệnh đề sau: Mệnh đề Đúng Sai a.
là một cấp số nhân với . ○ ○ b. Số hạng có 605 chữ số. ○ ○ c. Số hạng
có tích hai chữ số đầu tiên bằng 18. ○ ○
Câu 40. [Mức 3] Trong một tiết học Mỹ Thuật, bạn Châu có tờ giấy ( tờ mỗi màu xanh, đỏ, vàng) và
hình ngôi sao ( hình mỗi màu xanh, đỏ, vàng). Châu gắn ngẫu nhiên mỗi ngôi sao với
một tờ giấy bất kỳ, xác suất để không có ngôi sao nào được gắn với tờ giấy cùng màu với nó là , với
là phân số tối giản. Khi đó, giá trị của bằng? ➢ Điền đáp án: .
-=-=-=-=-=-=-=-HẾT-=-=-=-=-=-=-=-