PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG KIẾN XƯƠNG
NĂM HỌC 2024 – 2025 ***** Môn: Toán
(Thời gian làm bài: 120 phút)
Bài 1 (2,0 điểm).
1. Tính giá trị biểu thức 18 −1− 3− 2 2 + 2. Cho biểu thức: x 2 5 1 P = − − (với x ≥ 0;x ≠ 4) x + 3 x + x − 6 x − 2 a) Rút gọn P
b) Tìm tất cả các giá trị của x để 2 P > P x + my = 3m
Bài 2 (2,0 điểm). Cho hệ phương trình  2 mx − y = m − 2
1) Giải hệ phương trình khi m = 3
2) Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho:
a) Điểm A(x; y) thuộc đường tròn tâm O bán kính 5 (Với O(0; 0) là gốc tọa độ).
b) x; y là độ dài hai đường chéo của hình thoi có chu vi là 2 5 cm.
Bài 3 (2,0 điểm).
Trên mặt phẳng tọa độ cho parabol (P): y = 2
x và đường thẳng (d): y = −(m + 2)x + m + 4
a) Tìm tọa độ giao điểm của (d) và (P) khi m = - 4
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x ;x thỏa mãn: x < 0 ≤ x 1 2 1 2
Bài 4 (3,5 điểm).
1) Cho đường tròn tâm O và dây cung BC. Điểm A di chuyển trên cung lớn BC sao
cho tam giác ABC nhọn. Đường cao BE, CF của tam giác ABC cắt nhau tại H và cắt đường
tròn (O) theo thứ tự tại M, N.
a) Chứng minh tứ giác BCEF nội tiếp.
b) Chứng minh EF//MN và EF ⊥ OA.
c) Giả sử đường tròn (O) và dây BC cố định, xác định vị trí điểm A trên cung lớn BC
để diện tích tam giác AEH đạt giá trị lớn nhất.
2) Một bồn nước I-nox có dạng hình trụ với chiều cao 2m và chu vi đáy là π(m).
Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của vỏ
bồn nước và lấy π ≈ 3,14).
Bài 5 (0,5 điểm). +
Tìm giá trị nhỏ nhất của biểu thức: 1 4 x 3 A = 4x + − + 2026 với x > 0. 4x x +1 Hết
Họ và tên thí sinh:.........................................Số báo danh :........
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM TUYỂN SINH VÀO LỚP 10 THPT KIẾN XƯƠNG Năm học 2024 – 2025 Môn: Toán Bài 1 (2,0 điểm)
3. Tính giá trị biểu thức 18 −1− 3 − 2 2 x + 2 5 1 4. Cho biểu thức: P = − − (với x ≥ 0;x ≠ 4) x + 3 x + x − 6 x − 2
a) Rút gọn P b) Tìm tất cả các giá trị của x để 2 P > P Ta có 18 −1− 3 − 2 2 0,25đ = − − ( − )2 9.2 1 2 1 = 3 2 −1− 2 −1 Câu1: 0,5đ = 3 2 −1− ( 2 − ) 1 ( vì 2 >1) = 3 2 −1− 2 +1= 2 2 0,25đ
Vậy 18 −1− 3 − 2 2 = 2 2 x + 2 5 1 Ta có P = − − x + 3 x + x − 6 x − 2 Bài 1 (2,0 đ) x + 2 5 1 = − − x + 3 ( x + 3)( x − 2) x − 2 Câu 2a ( x +2)( x −2)−5−( x +3) 1,0đ = ( 0,25đ x + 3)( x − 2) x − 4 − 5 − x − 3 x − x −12 = ( = 0,25đ
x + 3)( x − 2) ( x + 3)( x − 2) ( x −4)( x +3) x − 4 = ( = 0,25đ x + 3)( x − 2) x − 2 x − 4
Vậy khi x ≥ 0;x ≠ 4, thì P = x 0,25đ − 2 x − 4 + Ta có P =
với điều kiện x ≥ 0;x ≠ 4 Câu2b x − 2 : 0,5đ + Để 2 P > P thì P(P − ) 1 > 0 −  −  2 − ( x − 4 x 4 x 4 ) ⇔ . −1 > 0 ⇔ > x − 2 x −  2  ( x −2) 0 2 0,25 đ ⇔ 2
− ( x − 4) > 0 ( vì ( − )2 x 2 > 0 x ∀ tmđkxđ
⇔ x − 4 < 0 ⇔ x <16
Két hợp với điều kiện ta được 0 < x <16  x ≠ 4 Vậy khi 0 < x <16  thì 2 P > P 0,25 x ≠ 4
(Không kết hợp điều kiện thì không cho điểm bước này) x + my = 3m
Bài 2 (2,0 điểm) Cho hệ phương trình  2 mx − y = m − 2
1) Giải hệ phương trình khi m = 3
2) Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho:
a) A(x; y) thuộc đường tròn tâm O bán kính 5 (Với O(0; 0) là gốc tọa độ).
b) x, y là độ dài hai đường chéo của hình thoi có chu vi là 2 5 cm.
Với m = 3, hệ phương trình trở thành: x + 3y = 9 x + 3y = 9 10  x = 30  ⇔  ⇔  Câu1: 3x  − y = 7 9  x − 3y = 21 x + 3y = 9 0,5 0,75,đ x = 3 x = 3 ⇔  ⇔  3  + 3y = 9 y = 2 x = 3
Vậy với m = 3 hệ phương trình có nghiệm là  0,25 y = 2 x + my = 3m (1) Bài 2  2 mx − y = m − 2 (2) (2,0 đ) Câu 2
0,75.đ + Từ (1) => x = 3m – my (3)
Thế (3) vào (2) ta được: m(3m – my) - y = m2 – 2
 3m2 – m2y – y = m2 – 2
 – m2y – y = - 3m2 + m2 – 2  (m2 + 1)y = 2m2 + 2  (m2 + 1)y = 2(m2 + 1)
 y = 2 (do (m2 + 1) > 0 với mọi m)
+ Thay y = 2 vào (3) ta được x = m
Vậy với mọi m, hệ phương trình luôn có nghệm duy nhất là 0,5 (x ; y) = (m; 2)
+ Ta có A(m ; 2). Để A(m ; 2) thuộc đường tròn tâm O bán kính 5 thì OA = 5  OA2 = 5  m2 + 22 = 5  m2 = 1  m = 1 ± 0,25 Vậy m = 1 ± thỏa mãn đề bài
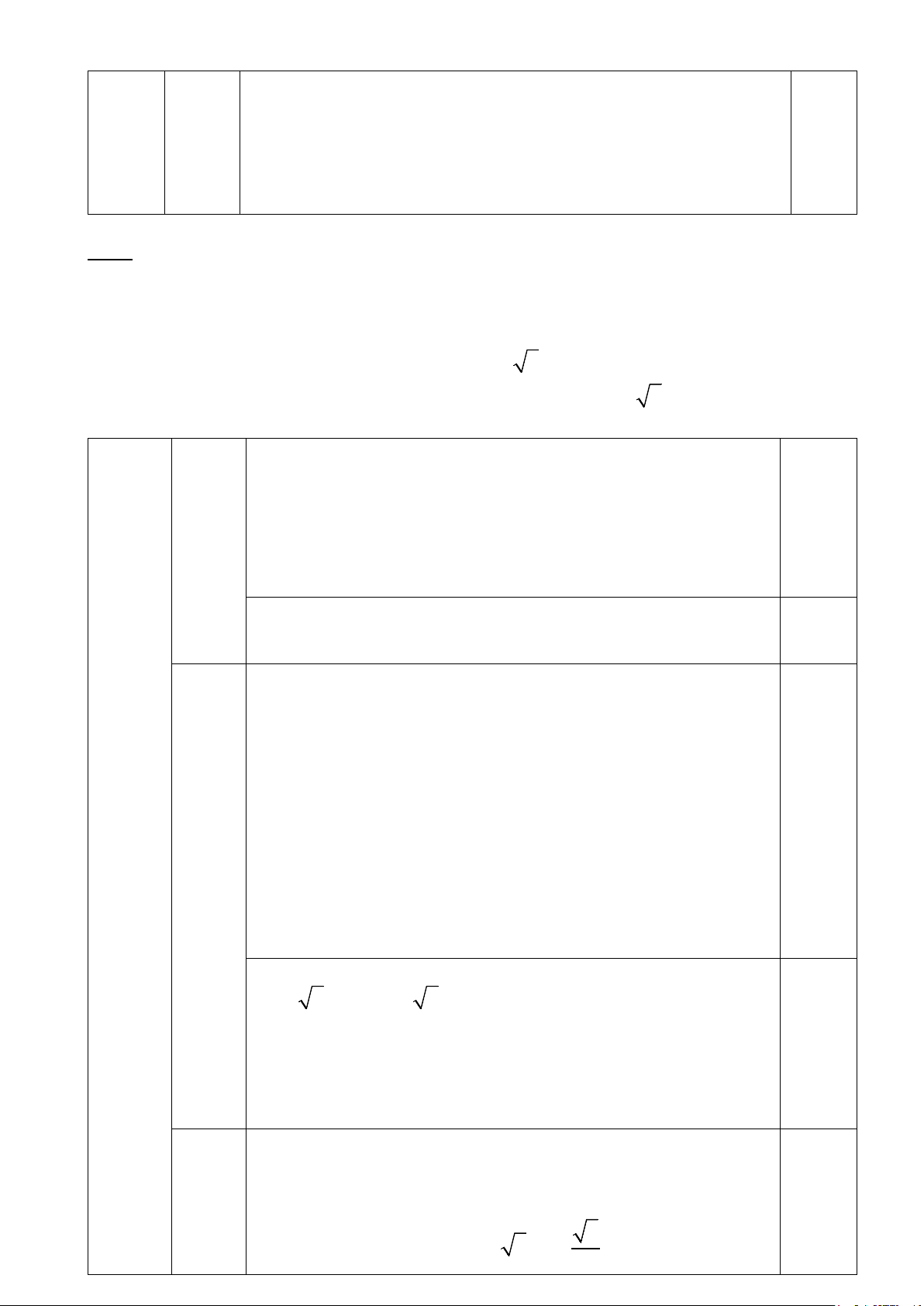
Câu 3: Do x, y là độ dài hai đường chéo của hình thoi nên 0,5đ x > 0 m > 0 0,25  ⇔  ⇔ m > 0 y > 0 2 > 0 (ld) 5
Độ dài cạnh của hình thoi là 2 5 : 4 = 2 B 5 2 y 2 A x O C 2 D
Do hai đường chéo hình thoi vuông góc với nhau tại trung điểm
của mỗi đường nên ta có phương trình: 0,25 2 2 2  x   y   5  2 2 + =       ⇔ x + y = 5  2   2  2    m2 + 22 = 5  m2 = 1  =  m 1 (tm)  m = 1 −  (ktm)
Vậy m =1 thỏa mãn đề bài Bài 3 (2,0 điểm)
Trên mặt phẳng tọa độ cho parabol (P): y = 2
x và đường thẳng (d): y = −(m + 2)x + m + 4
a) Tìm tọa độ giao điểm của (d) và (P) khi m = - 4
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x ;x , thỏa mãn: x < 0 ≤ x 1 2 1 2
Thay m = - 4 vào (d) ta được:y = 2x
Khi đó phương trình hoành độ giao điểm của (d) và (P) là: 0,25 2 x = 2x 2 ⇔ x − 2x = 0 Câu a ⇔ x(x − 2) = 0 0,5 1đ x = 0 x = 0 ⇔ ⇔  x 2 0  − = x = 2
Với x = 0 => y = 0 => (0; 0)
Với x = 2 => y = 4 => (2; 4) Bài 3
Vậy với m = - 4 thì tọa độ giao điểm của (d) và (P) là (0; 0); (2; 4) 0,25 (2,0 đ)
Câu b + Phương trình hoành độ giao điểm của (d) và (P) là: 0,25 1đ 2 x = −(m + 2)x + m + 4 2
⇔ x + (m + 2)x − m − 4 = 0 (*) + Tính được ∆ = ( + )2 m 4 + 4 > 0 m ∀
=> pt luôn có 2 nghiệm phân biệt x ;x với mọi m 1 2 x + x = −m − 2 ( ) 1
+ Theo hệ thức Vi-ét, ta có 1 2  x .x = −m −  4 (2) 1 2
+ Để x < 0 ≤ x ta xét 2 trường hợp sau: 1 2
TH1: Phương trình đã cho có 2 nghiệm x ;x thỏa mãn: 0,25 1 2 x < 0;x = 0 1 2 .
Thay x2 = 0 vào (2) ta được : −m − 4 = x .0 ⇔ m = 4 − 1
Thay m = - 4; x = 0 vào (1), ta được 2 x + 0 = − 4 − − 2 ⇔ x = 2 1 ( ) 1
Ta thấy x = 2 > 0 (không thỏa mãn x < 0;x = 0 ) 1 1 2 => m = -4 (không tm)
Tr.h2: Phương trình đã cho có 2 nghiệm x ;x thỏa mãn 0,25 1 2 x < 0 < x 1 2
=> phương trình đã cho có 2 nghiệm trái dấu
 1.(- m - 4) < 0 ⇔ m > 4 −
Vậy với m > - 4 để phương trình có 2 nghiệm x ;x , thỏa mãn: 0,25 1 2 x < 0 ≤ x 1 2 Bài 4 ( 3,5 điểm)
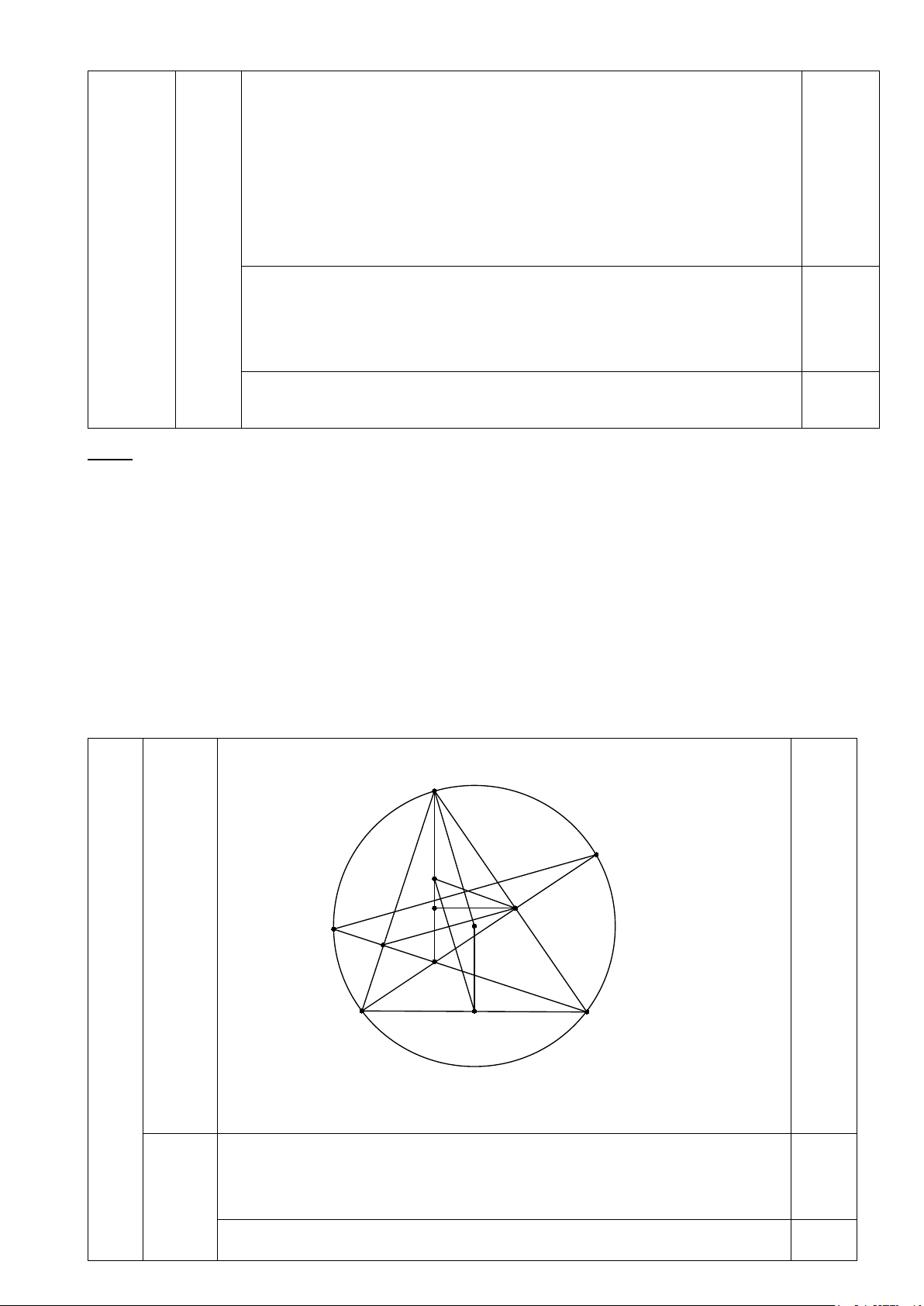
1. Cho đường tròn tâm O và dây cung BC. Điểm A di chuyển trên cung lớn BC sao cho
tam giác ABC nhọn. Đường cao BE, CF của tam giác ABC cắt nhau tại H và cắt đường tròn (O) theo thứ tự tại M,N
a) Chứng minh tứ giác BCEF nội tiếp. b) Chứng minh EF//MN và EF ⊥ OA.
c) Giả sử đường tròn (O) và dây BC cố định, xác định vị trí điểm A trên cung lớn BC để
diện tích tam giác AEH đạt giá trị lớn nhất.
2. Một bồn nước I-nox có dạng hình trụ với chiều cao 2m và chu vi đáy là π(m). Hỏi bồn
nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn nước và lấy π ≈ 3,14) A M I E D N O F H Bài 4 B K C (3.5 đ) Xét tứ giác BCEF có: Câu1a.  0 BFC = 90 (CF ⊥ AB) 0,5 đ 1,0đ  0 BEC = 90 (BE ⊥ AC) =>  =  ( 0 BFC BEC = 90 ) 0,25đ
=> tứ giác BCEF nội tiếp (Tứ giác có hai đỉnh F và E kề nhau cùng 0,25đ
nhìn cạnh BC dưới hai góc bằng nhau)
Ta có tứ giác BCEF nội tiếp (chứng minh trên) =>  = 
FEB FCB ( 2 góc nội tiếp cùng chắn  BF) 0.5 Mà  = 
NMB FCB (2 góc nội tiếp cùng chắn  BN của (O)) =>  =  =  FEB NMB( FCB) 0,25 Câu 1b 1,5đ
Mà 2 góc này ở vị trí đồng vị => MN//EF
Ta có tứ giác BCEF nội tiếp (chứng minh trên) =>  = 
EBF ECF ( 2 góc nội tiếp cùng chắn  EF) Hay góc  =  ABM ACN Xét (O) có:  =  ABM ACN (cmt) =>  = 
AM AN (các góc nội tiếp bằng nhau chắn các cung bằng nhau) 0.5
=> đường kính OA ⊥ MN ( quan hệ giữa đường kính, dây và cung) Mà MN //EF (cmt) => OA ⊥ EF 0,25
Gọi I, K theo thứ tự là trung điểm của AH và BC
HS chứng minh được: I, K lần lượt là tâm đường tròn ngoại tiếp tứ 0,25 giác AEHF và BCEF.
Mà 2 đường tròn này cắt nhau tại E,F
=> KI ⊥ EF ( tính chất đường nối tâm) Mà OA ⊥ EF (cmt) => OA //KI( ⊥ EF) (1)
Câu Xét (O) có KB = KC ; K ≠ 0 1c:
=> OK ⊥ BC ( quan hệ vuông góc đường kính dây cung)
0.5đ Mà AH ⊥ BC ( H là giao điểm 2 đường cao BE,CF của ∆ ABC) => AH //OK ( ⊥ BC) Hay AI//OK (2)
Từ (1), (2) => tứ giác AOKI là hình bình hành => AI = OK => AH = 2OK
∆ AEH vuông tại E, có I là trung điểm của AH 1
=> EI = AH = AI = OK (không đổi) 2
Kẻ ED ⊥ AH, ta luôn có ED ≤ EI Diện tích AE ∆ H là : 1 1 S = AH.ED ≤ AH.EI AEH 2 2 2 ⇒ S ≤ OK.OK = OK AEH (không đổi)
Dấu bằng xảy ra  ED = EI
 ∆ AEH vuông cân tại E   0 HAC = 45   0 ACB = 45
Vậy điểm A trên cung BC lớn sao cho  0 ACB = 45 thì diện tích AE ∆
H đạt giá trị lớn nhất.
Câu 2 Bán kính đáy của bồn nước là : 0,25 0,5đ C π 1 C = 2 R π ⇒ R = = = (m) 2π 2π 2
Thể tích của bồn nước là: 0,25 2  1 2 V .R .h 3,14.  = π ≈ .2 =   1,57( 3 m )  2 
Vậy bồn nước này đựng đầy được 1,57 m3 nước. Bài 5 ( 0,5 điểm) +
Tìm giá trị nhỏ nhất của biểu thức: 1 4 x 3 A = 4x + − + 2026 với x > 0. 4x x +1
+ Do x > 0, áp dụng bất đẳng thức AM-GM ta có 1 1 4x + ≥ 2 4x. = 2 (1) 4x 4x ( 0,25 − + + − + − )2 2 x 1 4 x 3 4x 4 4x 4 x 1 + Ta có = = 4 − ≤ 4 x +1 x +1 x +1 4 x + 3  − ≥ 4 − (2) x +1
Từ (1) và (2) => A ≥ 2024  1 4x = 1 Dấu “=” có khi  4x ⇔ x = (tm) 0,25 4 2 x −1= 0 1
Vậy MinA = 2024 đạt được khi x = 4
Lưu ý: Trên đây chỉ là hướng dẫn chấm cho 1 phương án, các cách làm khác đúng, lập luận
chặt chẽ vẫn cho điểm tối đa. Bài hình số 4.1 không vẽ hình hoặc sai hình không chấm.
Bài hình 4.2 không cần hình vẽ minh hoạ.
Điểm bài thi là tổng điểm các bài thành phần, không làm tròn.