Đề thi thử Toán tuyển sinh lớp 10 năm 2024 – 2025 trường THCS Thái Thịnh – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi thử môn Toán tuyển sinh vào lớp 10 THPT năm học 2024 – 2025 trường THCS Thái Thịnh, thành phố Hà Nội; kỳ thi được diễn ra vào ngày 14 tháng 05 năm 2024; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2024-2025
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
TRƯỜNG THCS THÁI THỊNH
KỲ THI THỬ TUYỂN SINH LỚP 10 THPT NĂM HỌC 2024 – 2025 Môn thi: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 14/5/2024
Thời gian làm bài: 120 phút Câu I (2,0 điểm) x 3 x 4 x Cho hai biểu thức A và B
với x 0; x 1; x 9 x 1 x 3 x 9
1) Tính giá trị của biểu thức A khi x 25 .
2) Rút gọn biểu thức P . A B .
3) Tìm các số tự nhiên x để P nhận giá trị âm. Câu II (2,0 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một đoàn xe vận tải dự định điều một số xe cùng loại để vận chuyển 40 tấn hàng. Lúc sắp
khởi hành đoàn xe được giao thêm 14 tấn hàng nữa. Do đó đoàn xe phải điều thêm 2 xe cùng
loại trên và mỗi xe phải chở thêm 0,5 tấn. Tìm số lượng xe phải điều theo dự định, biết mỗi
xe đều chở số lượng hàng như nhau và mỗi xe chở không quá 3,5 tấn hàng.
2) Một chiếc bình thủy tinh có dạng hình trụ với đường kính đáy là 6cm và chiều cao là 22cm.
Tính thể tích của chiếc bình (coi độ dày của thành bình không đáng kể và lấy 3,14 ). Câu III (2,5 điểm) 3 y 9 5 x
1) Giải hệ phương trình: 2 2 3 y 9 4 x 2
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d ) : y (m 2)x m 4 và parabol 2 (P) : y x
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại 2 điểm phân biệt.
b) Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt ( A x ; y ), B(x ; y ) 1 1 2 2 x 2 x 2 sao cho 1 2 m . x x 2 1
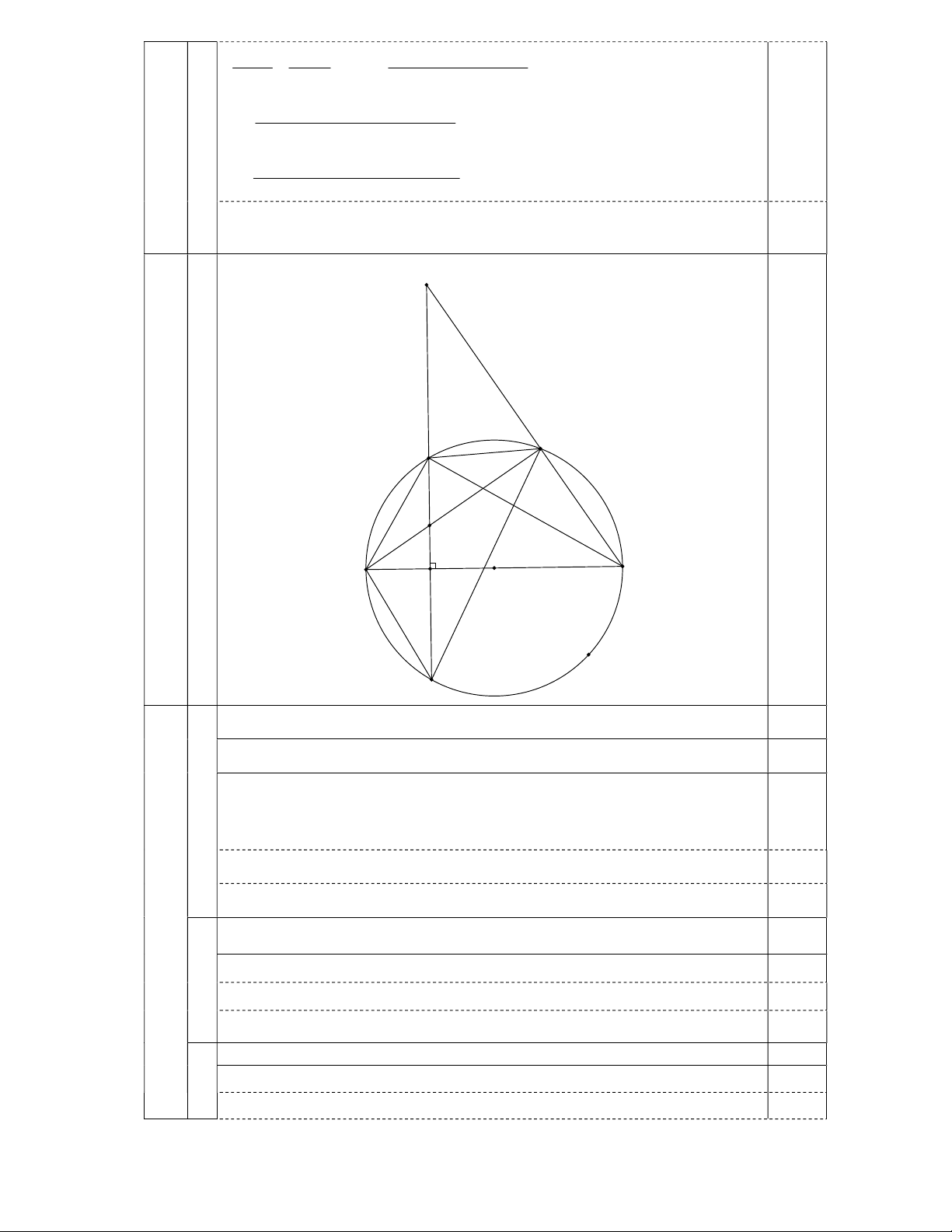
Câu IV (3,0 điểm) Cho đường tròn tâm O đường kính AB 2R . Gọi C là trung điểm của O , A
qua C kẻ dây MN của (O) vuông góc với OA tại C . Gọi K là điểm tùy ý trên cung nhỏ BM ,
H là giao điểm của AK và MN . Tia BK cắt đường thẳng MN tại điểm P .
1) Chứng minh tứ giác BCHK là tứ giác nội tiếp. 2) Chứng minh MHK ANK .
3) Chứng minh AMH đồng dạng với AKM và HM.PN HN.PM . Câu V (0,5 điểm) 2
Tìm giá trị nhỏ nhất của biểu thức 2 P a a 2024 . 2 a 1
-----------------HẾT-----------------
Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh:………………………………………………………Số báo danh:………………..
Họ tên và chữ kí của cán bộ coi thi số 1:
Họ tên và chữ kí của cán bộ coi thi số 2: TRƯỜNG THCS THÁI THỊNH
KỲ THI THỬ TUYỂN SINH LỚP 10 THPT NĂM HỌC 2024 – 2025 Môn thi: TOÁN Ngày thi: 14/5/2024
Thời gian làm bài: 120 phút HƯỚNG DẪN CHẤM (gồm 04 trang) HƯỚNG DẪN CHUNG
+) Điểm toàn bài để lẻ đến 0,25.
+) Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm.
+) Các tình huống phát sinh trong quá trình chấm do Hội đồng chấm thi quy định, thống nhất bằng biên bản. Bài Ý Đáp án Điểm
Tính giá trị của biểu thức A khi x 25 0,5
Thay x = 25 (tmđk) vào biểu thức A 0,25 1 25 3 Tính được A 2 0,25 25 1
Rút gọn biểu thức P biết P . A B 1,0 x x x 3 3 4 x . A B .
x 1 ( x 3)( x 3) ( x 3)( x 3) 0,5 x 3 x x 2 . x 1 ( x 3)( x 3) x x x 1 3 I . 0,25 x 1 ( x 3)( x 3) x 0,25 x 3
Tìm giá trị của x để P nhận giá trị âm. 0,5 x P 0 0 x 3 x 0 0,25 3 x 3 0 x 0 x 0 x 3 0 x 9 0,25
Kết hợp Đkxd: x 2;3;4;5;6;7; 8
Tìm số lượng xe phải điều theo dự định 1,5
Gọi số xe ban đầu là x (xe, x N *) 0,25
II 1 Số hàng ban đầu mỗi xe dự định chở là 40 (tấn) x 0,25
Số xe sau khi được bổ sung là x 2 (xe)
Số hàng thực tế mỗi xe chở là 54 (tấn) x 2
Lập luận để có phương trình 54 40 1 x 2 x 2 0,5 2 x 26x 160 0
Giải phương trình được x 10 hoặc x 16 0,25
Do mỗi xe chở không quá 3,5 tấn nên số xe ban đầu là 16 xe 0,25
Hoa có thể đựng được 500ml nước trong bình của mình hay không 0,5
Thể tích của bình nước là: 2 V r h 0,25 2 2 6 3 V 3,14. .22 621,72(cm ) 2 0,25
Vậy thể tích của bình khoảng 621,72 cm3 Giải hệ phương trình 1,0 ĐKXĐ: x 2; y 9 0,25 3 y 9 5 x 2 1 Đặt a; y 9 b 2 x 2 3 y 9 4 0,25 x 2 1 3a b 5 a 1 Giải hệ 2a 3b 4 b 2 1 1 x 1 x 2 0,25 y 13 y 9 2
Đối chiếu ĐK và kết luận:
Vậy hệ pt có nghiệm là (x; y) là (-1; 13) 0,25 III
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại 2 điểm 0,75 phân biệt.
Xét phương trình hoành độ giao điểm của (d) và (P) 0,25 2 2
x (m 2)x m 4 x (m 2)x m 4 0 Tính được 2 m 20 0,25 0 m nên suy ra đpcm 0,25
2 b)Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt x 2 x 2 ( A x ; y ), B(x ; y ) sao cho 1 2 m 0,75 1 1 2 2 x x 2 1 x x m 2 Theo Viet: 1 2 x x m 4 1 2 0,25 x 2 x 2 1 2
m ĐK: x x 0 m 4 x x 1 2 2 1 2 2 x 2 x 2 x x 2(x x ) 1 2 1 2 1 2 m m x x x x 2 1 1 2 2
(x x ) 2x x 2(x x ) 1 2 1 2 1 2 m 0,25 x x 1 2 2
(m 2) 2(m 4) 2(m 2) m m 4
Giải được m 2(t / m) và kết luận 0,25 P K M H A C B O N
Chứng minh tứ giác BCHK là tứ giác nội tiếp 1,0
Vẽ hình đúng đến câu a 0,25 Chứng minh 0 HKB 90 1 0,25 Xét tứ giác BCHK có: HCB 0 HKB 180
Mà hai góc này ở vị trí đối nhau 0,25
=> Tứ giác BCHK nội tiếp 0,25 IV MHK Chứng minh ANK . 1,0 2 Chứng minh MHK KBC 0,5 Chứng minh KBC ANK 0,25 Suy ra MHK ANK 0,25
Chứng minh AMH đồng dạng với AKM và HM.PN HN.PM . 1,0
3 Chứng minh cung AM= cung AN. 0,25
Chứng minh AMH đồng dạng với AKM 0,25
Chứng minh KH là tia phân giác HM KM MKN suy ra: HN KN 0,25
Chứng minh KP là tia phân giác ngoài PM KM MKN suy ra: PN KN
Từ đó suy ra HM.PN HN.PM 0,25 2
Tìm giá trị nhỏ nhất của biểu thức 2 P a a 2024 2 a 1 0,5 4 2 2P 2a 2a 4048 2 a 1 4 2 a 2a 1 2 a 1 4046 0,25 2 a 1 V
+) a a a 2 2 2 1
1 0 , dấu bằng xảy ra khi a 1. 4 4 +) 2 a 1 2 2 a 1 .
4 , dấu bằng xảy ra khi 2 2 a 1 a 1 4 a 1 2 a 1 . 0,25 2 a 1 a 1
Do đó 2P 4050 P 2025
Vậy GTNN của P bằng 2025 khi a 1.