Đề thi thử Toán tuyển sinh lớp 10 năm 2025 – 2026 phòng GD&ĐT Anh Sơn – Nghệ An

UBND HUYỆN ANH SƠN
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2025-2026 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(không kể thời gian giao đề) Câu 1. (1,5 điểm)
a) Một trường THCS ghi lại nhóm máu của các giáo viên chuẩn bị cho đợt hiến máu
tình nguyện kết quả như sau;
O, A, O, AB, O, O, B, A, B, B, O, O, B, B, O
B, O, O, O, B, A, B, O, O, O, A, B, O, O, B
Có bao nhiêu nhóm máu? Nhóm máu nào phổ biến nhất? Lập bảng tần số cho dãy dữ liệu trên.
b) Gieo một con xúc xắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau: Số chấm xuất hiện 1 2 3 4 5 6 Số lần 17 18 15 14 16 20
Hãy tìm xác suất thực nghiệm của sự kiện số chấm xuất hiện là số chẵn. Câu 2 (2,0 điểm).
a) Rút gọn biểu thức A  12  3 27  5 48 ;
b) Rút gọn biểu thức: B =  1 1  x − 3 + ⋅ 
(với x > 0, x ≠ 9 )  x 3 x 3  − +  x
c) Cho hàm số y = ax + b. Tìm a và b để đồ thị của hàm số song song với đường thẳng
y = -3x + 5 và cắt trục hoành tại điểm có hoành độ bằng 2. Câu 3 (2,0 điểm).
a) Hội trường của một ủy ban xã có tổng số ghế ban đầu là 400 ghế, được sắp xếp
thành các dãy, mỗi dãy có số ghế bằng nhau. Do thực hiện việc sát nhập hai xã gần nhau
nên cần tăng thêm số ghế. Họ lắp thêm 2 dãy ghế trong hội trường và mỗi dãy tăng
thêm 2 ghế, nên tổng số ghế tăng thêm 84 ghế. Hỏi ban đầu hội trường này có bao nhiêu dãy ghế?
b) Thuốc lá điển tử có hại rất lớn đối với người dùng, đặc biệt gây hậu quả
nghiêm trọng đối với trẻ vị thành niên, gây suy giảm trí nhớ, ảnh hưởng đến bệnh
tim. . Trong đợt truy quét tội phạm, công an đã bắt được Nguyễn Văn A bán thuốc lá
điện tử, thu được 12 hộp gồm 2 loại , loại hộp to 20 điếu, loại hộp nhỏ 15 điếu. Tổng số
điếu thu được từ 12 hộp trên là 200 điếu. Hỏi công an thu được bao nhiêu hộp mỗi loại? c) Cho phương trình : 2
3x + 4x −1= 0 có hai nghiệm phân biệt x1 , x2 . Không giải 3 2 x .x ( 2 1− 3x 1 2 2 )
phương trình hãy tính giá trị biểu thức : P = 2 2 x + x 1 2
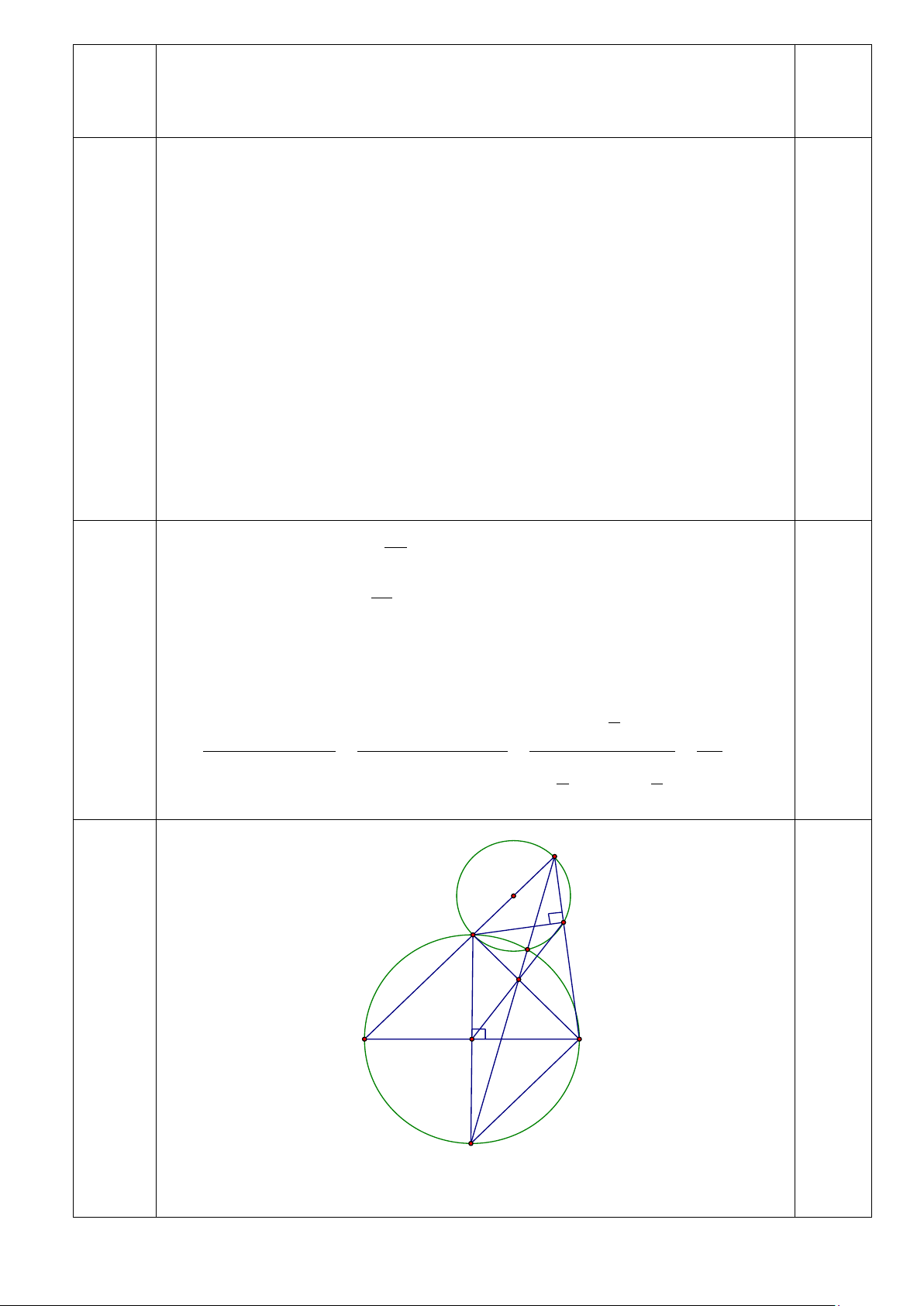
Câu 4 (3,0 điểm). Cho đường tròn (O) có hai đường kính AB và MN vuông góc với nhau.
Trên tia đối của tia MA lấy điểm C khác điểm M. Kẻ MH vuông góc với BC (H ∈ BC).
a) Chứng minh MHBO là tứ giác nội tiếp.
b) MB cắt OH tại E. Chứng minh ME.HM = BE.HC.
c) Gọi giao điểm của đường tròn (O) và đường tròn ngoại tiếp tam giác MHC
là K. Chứng minh ba điểm C, K, E thẳng hàng.
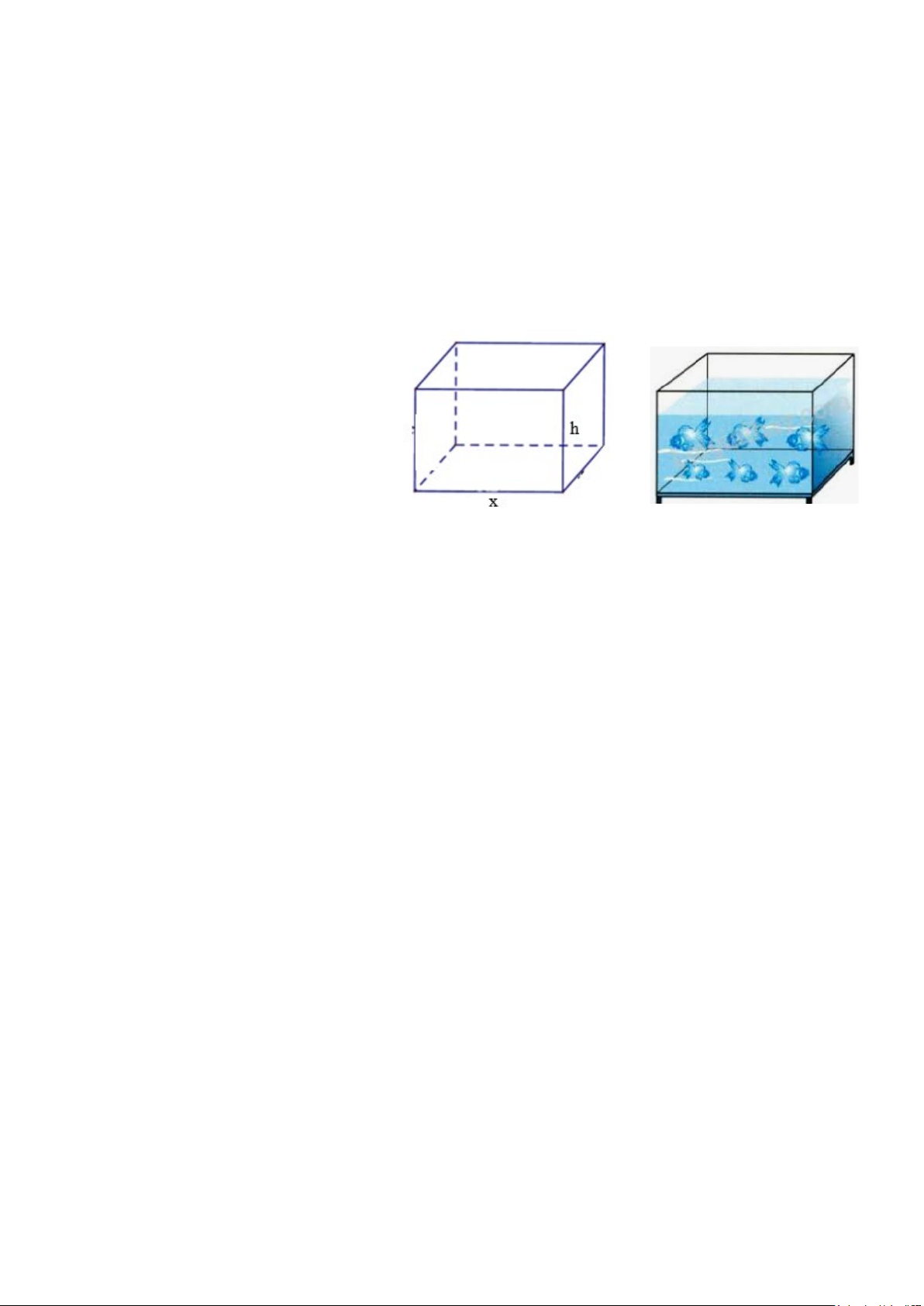
Câu 5 (1,5 điểm). Một khách hàng đặt một người thợ làm một chiếc bể hình hộp chữ
nhật không có nắp, đáy là hình vuông có cạnh là x và chiều cao của bể là h.
a) Nếu chiều cao của bể bằng độ
dài cạnh đáy và chu vi mặt đáy
là 2m. Tính thể tích của bể cá?
b) Theo đơn đặt hàng của khách thì bể cá được làm bằng kính trong suôt và phải chứa
được 4m3 nước. Hỏi chiều dài của cạnh đáy và chiều cao của bể bằng bao nhiêu để
người thợ tiết kiệm chi phí và nguyên vật liệu nhất? --- Hết ---
Họ và tên thí sinh:.............................................. Số báo danh:.............................
HƯỚNG DẪN VÀ BIỂU ĐIỂM CHẤM MÔN TOÁN Câu Nội dung Điểm
a, Có bốn nhóm máu là A, B, AB, O 0,25
Nhóm máu phổ biến nhất là nhóm máu O 0,25 Bảng tần số: Nhóm máu A B O AB Câu 1 Tần số 4 10 15 1 0,5
(1,5 đ) Các mặt có số chấm là số chẵn của con xúc xắc là mặt 2,4,6. Xác suât là: 0,5 18 +14 + = 20 P = 52 = 52% 100 100 Câu 1
A  12  3 27  5 48 (2,0 đ) 0,5
a) ( 0,75) Ta có  2 3  9 3  20 3 0,25  9 3 b) (0,75) x + 3 + x − 3 x − 3 B = ( x − )( x + ). 3 3 x 0,5 2 x x − 3 2 B = ( =
x + 3)( x −3). x x + 3 0,25
c) Để đồ thị của hàm số y = ax + b song song với đường thẳng y = -3x + 5 thì: a = a' a = 3 −  ⇔ 0,25 b b' b  ≠  ≠ 5 (*)
Đồ thị của hàm số y = ax + b cắt trục hoành tại điểm có hoành độ bằng
2 tức là khi x = 2 thì y = 0. Thay vào ta có:
0 = -3.2 + b => b = 6 (TM (*)) 0,25 Vậy a = -3; b = 6
Hàm số đã cho là: y = -3x +6 Câu 3
a) Gọi số dãy ghế ban đầu là x ( dãy) ( x∈ N ; x > 0)
(2,0 đ) Ban đầu, số ghế ở mỗi dãy là: 400 (ghế) Ý a x 0,25
(0,75 đ) Số ghế ở mỗi dãy sau khi thêm là: 484 x + 2 Theo bài ra ta có pt: 400 484 + 2 = 0,25 x x + 2 2
⇔ x − 40x + 400 = 0 2
⇔ (x − 20) = 0 ⇔ x = 20(TM ) 0,25
Vậy số dãy ghế ban đầu của hội trường là: 20 dãy Ý b
(0,75 đ) Gọi số hộp thuốc lá loại to mà công an thu được là x (hộp) ( * x ∈ N x <12) 0,25
Gọi số hộp thuốc lá loại nhỏ mà công an thu được là y (hộp) ( * y∈ N y <12)
Vì thu được 12 hộp gồm 2 loại nên ta có phương trình: x + y =12(1)
Số điếu thuốc trong các hộp to là 15x ( điếu)
Số điếu thuốc trong các hộp nhỏ là 20y ( điếu) 0,25
Vì tổng số điếu thu được từ 12 hộp trên là 200 điếu ta có phương trình 20x + 15y = 200 (2)
Từ (1) và (2) ta có hệ phương trình x + y =12 
20x +15y = 200 0,25
Giải hệ pht x = 4; y = 8 (TM)
Vậy loại to có 4 hộp , nhỏ có 8 hộp Ý c  4 x + x − = (0,5 đ)  1 2 Theo viet ta có:  3  1 x .x −  = 1 2  0,25  3
Vì x là nghiệm của phương trình nên ta có: 2 2 2
3x + 4x −1= 0 ⇔1− 3x = 4x 2 2 2 2 3  1  0,25 3 2 x x ( 2 4. . 1 3x 4 x .x  −  − 1 2 2 ) (  3  2 − 1 2 )3 A = = = = 2 2 x + x
x + x − 2x .x  4   1  33 1 2 ( 1 2)2 2 1 2  −  − 2. − 3 3      Câu 4 C (3,0 đ) I M H K E A B O N 0,5 a)
Gọi F là trung điểm của MB suy ra MF = FB = MB (1) (1,0 đ) 2
Xét tam giác MOB vuông tại O có OF là đường trung tuyến ứng với 0,5
cạnh huyền MB nên OF = MB (2) 2 0,25
Tương tự ta có HF = MB (3) 2
Từ (1); (2); (3) suy ra bốn điểm O, M, H, B cùng thuộc đương tròn (F) 0,25
Hay tứ giác MHBO nội tiếp. b)
Áp dụng hệ thức lượng trong tam giác vuông BMC có MH là đường (1,0 đ) cao ta có: 2 = . ⇒ CH = MH MH CH BH (3) 0,25 MH BH
Tứ giác MHBO nội tiếp nên ta có:  MHO =  MBO  BMO =  BHO
( góc nt cùng chắn một cung ) 0,25 Mà: ∆ O
MB vuông cân tại O nên:  BMO =  MBO ⇒  MHO =  BHO
Nên HE là tia phân giác của tam giác MHB ta có: ME 0,25 = MH (4) BE HB Từ (3) và (4) CH ME ⇒ = ⇒ ME.MH = BE.CH MH BE 0,25 c)
Gọi tâm đường tròn ngoại tiếp ∆MHC là I, vì ∆MHC vuông tại H nên (0,5 đ)
đường tròn (I) có đường kính là MC. Vậy  0 MKC = 90 . Mà  MKN = 900
Suy ra ba điểm C, K, N thẳng hàng. (5) Ta có: ∆MHC ∆BMC 0,25 Nên CH = MC MH MB CH MC ME Mà MB = NB suy ra: = = MH NB BE
∆ MEC và ∆ BEN có  =  0
CME EBN = 90 và MC ME = BN BE
nên ∆MEC ∽∆BEN (c.g.c) ⇒  = 
MEC BEN mà M, E, B thẳng hàng nên C, E, N thẳng hàng (6) 0,25
Từ (5) và (6) ⇒ bốn điểm C, K, E, N thẳng hàng hay C, K. E thẳng hàng
Câu 5 Vì chu vi mặt đáy là 2m, ta có: 4x = 2 hay x = 0,5 (m) => h = 0,5 (m)
(1,5 đ) Thể tích bẻ cá là: 0,5
V = Sđ.h = (0,5)2.0,5 = 0,125 (m3)
Vậy thể tích của bể cá là 0,125 m3 0,5
Vì thể tích của bể cá theo đơn đặt hàng là 4m3, ta có: x2.h = 4 suy ra 4 h = 2 x 0,25
Vì đáy của bể là hình vuông nên diện tích các mặt bên của bể là các
hình chữ nhật có diện tích bằng nhau. Do đó, diện tích kính dùng để làm bể là: 2 4 2 16 2 8 8 2 S = S + S = 4.x.h + x = 4.x. + x = + x = + + x xq d 2 x x x x
Áp dụng BĐT Cauchy cho 3 số dương, ta có: 8 8 2 8 8 2 3 = + + ≥ 3 S x 3 . .x = 3 64 = 3.4 =12 0,25 x x x x Dấu ‘=” xảy ra: 8 2 3
= x hay x = 8 hay x = 2 khi đó h = 1(m) x
Vậy để người thợ tiết kiệm chi phí và nguyên vật liệu nhất thì bể có
cạnh đáy là 2m và chiểu cao là 1m
*Lưu ý: HS làm cách khác mà đúng vẫn cho điểm tối đa
Xem thêm: ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN
https://thcs.toanmath.com/de-thi-tuyen-sinh-lop-10-mon-toan
Document Outline

• TOAN
• TS 10