

Preview text:
SỞ GDĐT THÁI NGUYÊN
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT ĐỢT 1
TRƯỜNG THPT SÔNG CÔNG Năm học 2023-2024 MÔN: TOÁN HỌC
Thời gian làm bài: 120 phút, không kể thời gian giao đề
(Đề thi gồm có 01 trang)
Câu 1 ( 1,0 điểm). Không dùng máy tính cầm tay, rút gọn biểu thức: A 2 1 1 2 . 2 1
Câu 2 ( 1,0 điểm). Không dùng máy tính cầm tay, hãy giải phương trình: 2
x 3x x 1 . 2 x
Câu 3 ( 1,0 điểm). Cho hàm số y
có đồ thị là P. 2
a) Tìm các điểm M thuộc P, biết M có tung độ bằng 1.
b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số khi 2 x 4 .
x 2 y 3
Câu 4 ( 1,0 điểm). Không dùng máy tính cầm tay, hãy giải hệ phương trình: . 2x y 4 x 3 6 x 4
Câu 5 ( 1,0 điểm). Cho biểu thức B
với x 0 và x 1. x 1 x 1 x 1
a) Rút gọn biểu thức B . 1
b) Tìm x để B . 2
Câu 6 (1,0 điểm). Tìm tham số m để phương trình 2
mx x 1 0 có nghiệm duy nhất.
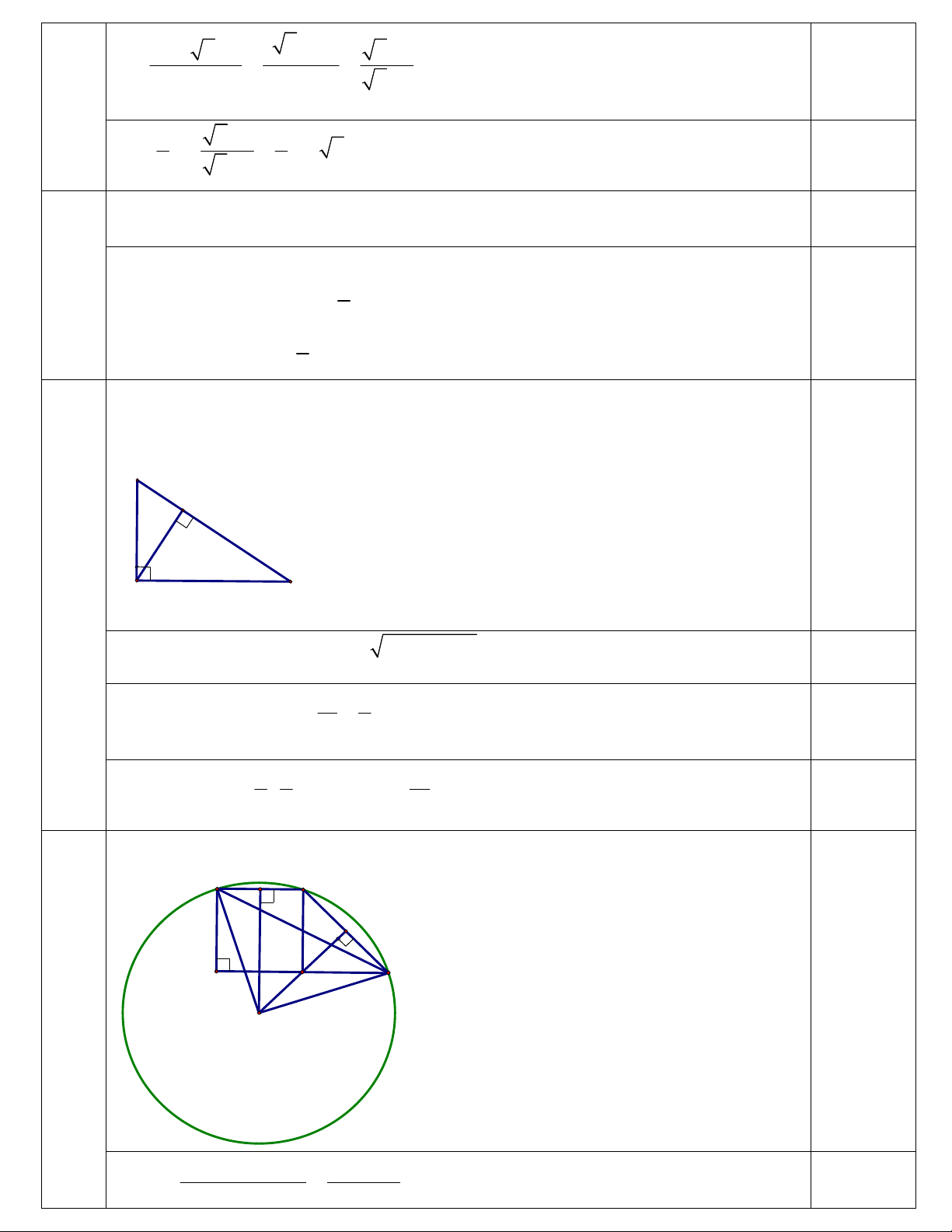
Câu 7 (1,0 điểm). Cho tam giác ABC vuông tại A, có đường cao AH . Biết AB 5cm ,
AH 3cm . Tính HB, HC và AC .
Câu 8 (1,0 điểm). Cho hình thang vuông ABCD có đường cao AD 2cm , AB 2cm và
CD 4cm . Tính diện tích hình thang và bán kính đường tròn ngoại tiếp tam giác ABC .
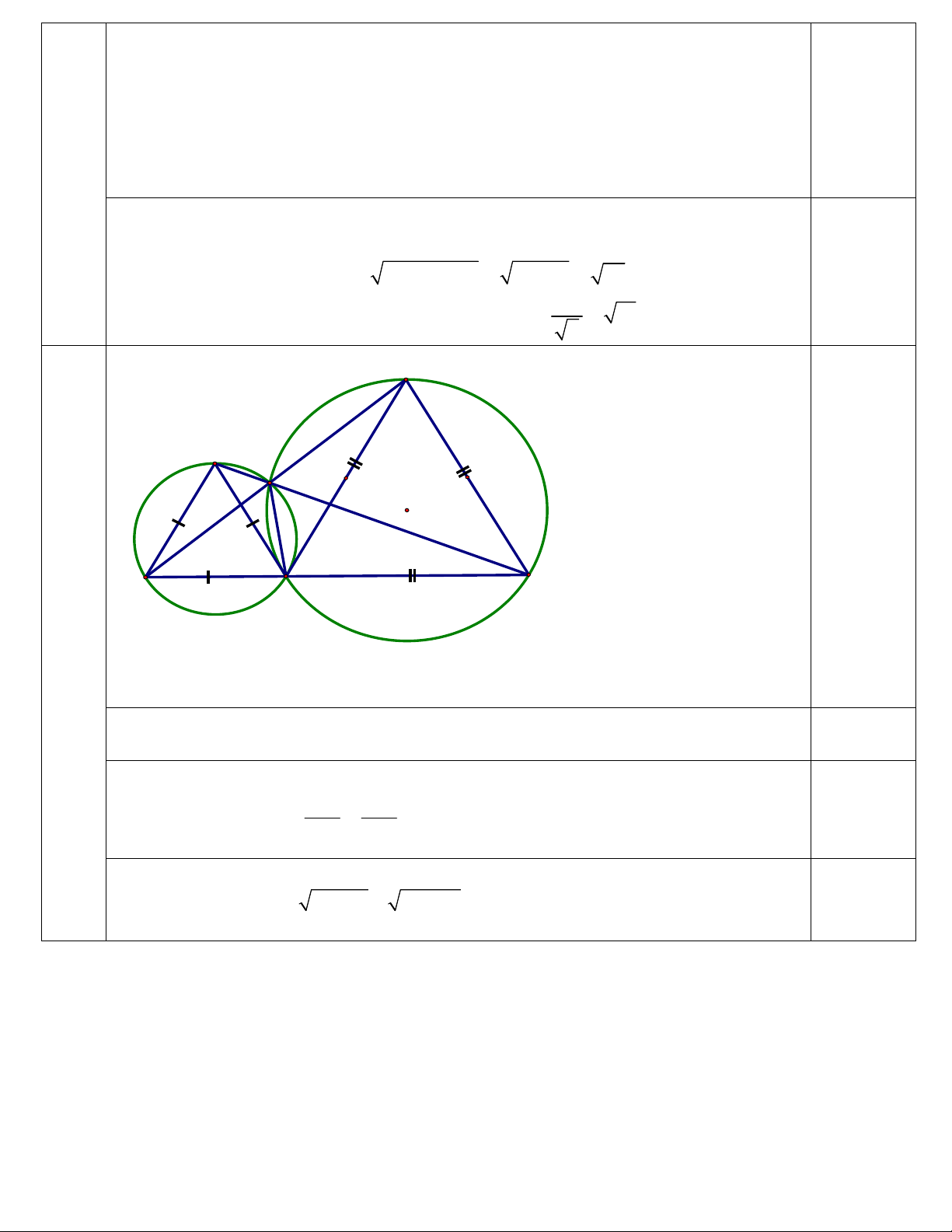
Câu 9 (1,0 điểm). Cho ba điểm ,
A M , B phân biệt, thẳng hàng và M nằm giữa , A B . Trên
cùng một nửa mặt phẳng bờ là đường thẳng AB , dựng hai tam giác đều AMC và BMD . Gọi
P là giao điểm của AD và BC . Chứng minh:
a) Tứ giác AMPC nội tiếp. b) C . P CB D . P DA AB .
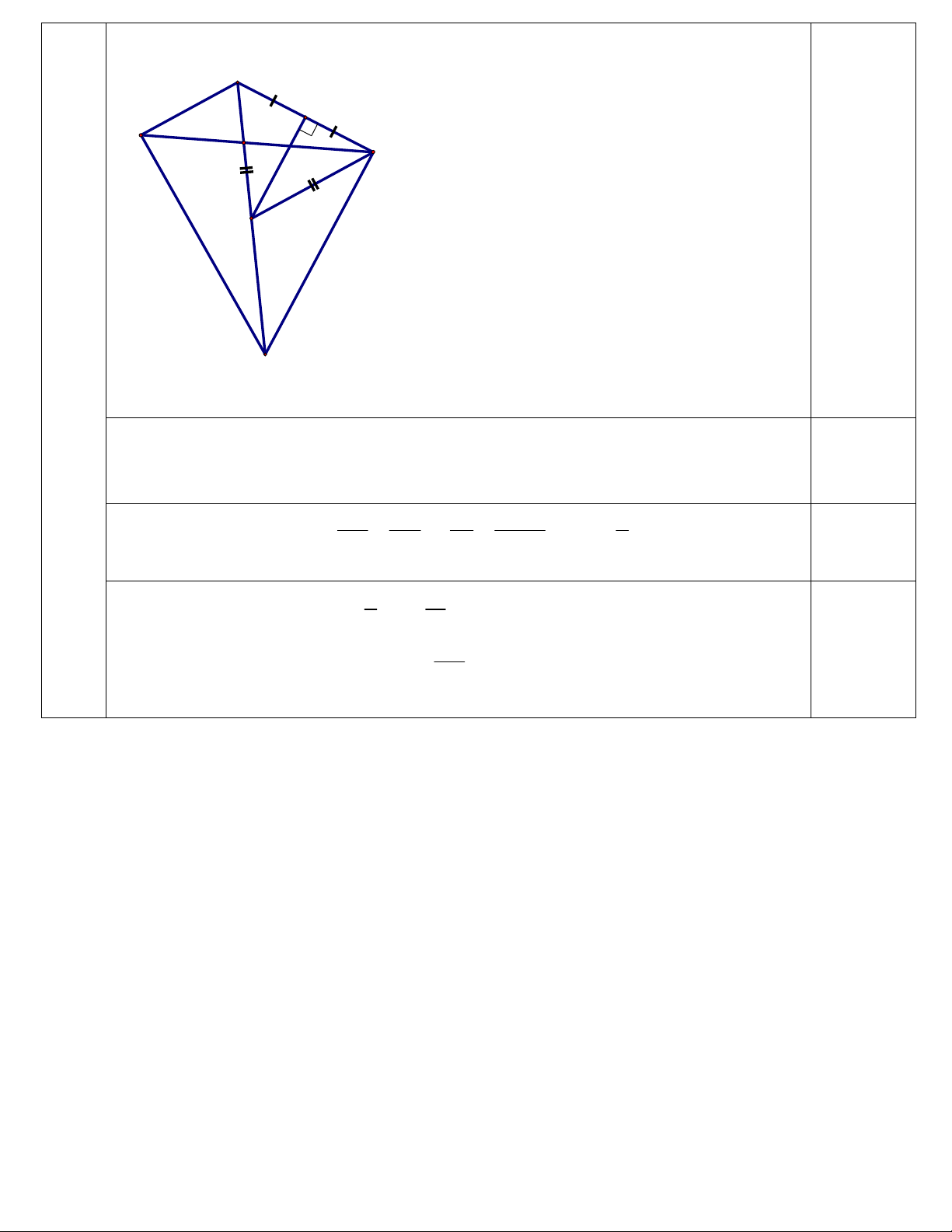
Câu 10 (1,0 điểm). Cho ABCD là một tứ giác nội tiếp có AC BC, AD 5cm . Hai đường
chéo AC, BD cắt nhau tại E sao cho BE 12cm và DE 3cm . Đường trung trực của đoạn
thẳng CD cắt đoạn thẳng BE tại I .
a) Chứng minh IC / / AD . b) Tính BCD . ……….HẾT……….
Họ và tên thí sinh:……………………………………………….Số báo danh:………………………. SỞ GDĐT THÁI NGUYÊN
ĐÁP ÁN ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
TRƯỜNG THPT SÔNG CÔNG Năm học 2023-2024 MÔN: TOÁN HỌC
(Đáp án gồm có 04 trang) CÂU ĐÁP ÁN ĐIỂM 1 A 2 1 1 2 1 2 2 1 2 1 0,5 2 1 2 1 2 . 0,5 2 Cách 1. 2
x 3x x
1 x 2x 3 0 . 0,5 x 0 0,5 x 0 3
3 . Vậy PT có 2 nghiệm phân biệt x 0 và x . 2x 3 0 x 2 2 Cách 2. 2
x x x 2 3
1 2x 3x 0 . 0,5 Ta có 9 0 . 0,5 3 9 3 9 3
PT có 2 nghiệm phân biệt x 0, x . 1 2 4 4 2 3 2 x 0,25
a) Tung độ của M bằng 1 nên y 1 . Ta có M 1 x 2 . M 2 M Vậy có 2 điểm 0,25
M thỏa mãn là M 2; 1 và M 2; 1 . 2 x
b) Theo tính đồng biến, nghịch biến của hàm số y ta có: 2 2 2 +) Với 2
x 0 0 y 0 y 2 . 0,25 2 2 4
+) Với 0 x 4 0 y 0 y 8 . 2 Như thế nếu 2
x 4 thì 0 y 8 .
Vậy giá trị nhỏ nhất của hàm số bằng 0 đạt được khi x 0 0,25
và giá trị lớn nhất của hàm số bằng 8 đạt được khi x 4 . 4
x 2 y 3
2x 4 y 6 5 y 1 0 2x y 4 2x y 4 2x y 4 0,5 y 2 x 1
. Vậy nghiệm của hệ phương trình là 1;2 . 2x y 4 y 2 0,5 5 x 0,25 x x
x 1 3 x 1 6 x 4 3 6 4 B x 1 x 1 x 1 x 1 x x x 2 1 2 1 x 1 . 0,5 x 1 x 1 x 1 1 x 1 1 B
x 3 x 9 (Thỏa mãn điều kiện). Vậy x 9 . 2 x 1 2 0,25 6
Với m 0 ta có PT x 1 0 x 1
(duy nhất). Vậy m 0 thỏa mãn. 0,5 Với m 0 , PT 2
mx x 1 0 có nghiệm duy nhất khi và chỉ khi 1
0 1 4m 0 m . 4 0,5 1
KL: m 0 hoặc m . 4 7 * Hình vẽ B 0,25 H A C 2 2 AB 5c ,
m AH 3cm BH
AB AH 4cm . 0,25 2 3 9 0,25 2 H .
B HC AH HC cm . 4 4 9 9 15 0,25 2
AC CH .CB 4 AC cm . 4 4 4 8 Hình vẽ A I B H 0,25 C D P O
AB CD.AD 2 4.2 0,25 2 S 6cm . ABCD 2 2
Gọi I , H lần lượt là trung điểm AB, BC và O là tâm đường tròn ngoại tiếp A
BC . Ta có OI AB, OH BC .
Gọi P là trung điểm CD , suy ra tam giác BCP vuông cân tại P và 0,25 135o ABC .
Trong tứ giác OIBH , ta có 360o
90o 90o 135o 45o IOH .
Xét tam giác OAC có , 2 90o OA OC AOC IOH , suy ra A OC vuông cân tại O . 0,25 Mặt khác trong 2 2 2 2 ADC : AC AD DC 2 4 20 . AC
Vậy bán kính đường tròn ngoại tiếp A
BC là R 10cm . 2 9 D C P 0,25 A M B Xét 2 tam giác
CMB và AMD có CM AM , MB MD và 120o CMB AMD Suy ra C
MB AMD .
Tứ giác AMPC có
PAM PCM (cmt) nên nó là tứ giác nội tiếp. 0,25
Xét hai tam giác CPM và CMB có C chung, 120o CPM CMB 0,25 CP CM 2 C PM C MB C .
P CB CM (1). CM CB
Tương tự, ta chứng minh được tứ giác BMPD nội tiếp và 2 D .
P DA DM (2). Từ (1) và (2), suy ra . CP CB .
DP DA CM DM AM BM AB . 0,25 10 D H A E C I 0,25 B
Do ABCD nội tiếp nên BAC BDC .
Do tam giác ABC cân tại C và tam giác ICD cân tại I nên o o
CID 180 2IDC 180 2BAC ACB . 0,25 Lại do
ACB ADB , ta suy ra
CID ADB . Vậy IC / / AD . IE IC IE IE 3 9
Theo định lí Talet, ta có: IE cm . ED AD 3 5 2 0,25 9 15
Ta tính được ID IE ED 3
cm và DB DE EB 3 12 15cm . 2 2 DB 0,25
Do I thuộc đoạn thẳng DB và ID
nên I là trung điểm DB . 2 Vậy 90o BCD . ……….HẾT……..
Document Outline
- thi thu vao 10-23-24
- dap an thi thu vao 10-2023




