Đề thi thử Toán vào 10 lần 1 năm 2023 – 2024 phòng GD&ĐT Diễn Châu – Nghệ An

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO DIỄN CHÂU
ĐỀ THI THỬ VÀO LỚP 10 THPT LẦN 1 NĂM HỌC 2023-2024
Môn: TOÁN (Thời gian làm bài: 120 phút)
------------------------------
Câu 1. (2,5 điểm)
a) Tính giá trị biểu thức: A = 1012 8 2 3 + − 12 2  3 1  x + 2
b) Rút gọn biểu thức: B = +   :
với x ≥ 0, x ≠ 1.  x −1 x +1 x −1
c) Cho hàm số y = ax + b. Tìm a và b để đồ thị của hàm số song song với
đường thẳng y = -2x +5 và cắt trục hoành tại điểm có hoành độ bằng 2.
Câu 2. (2,0 điểm) a) Giải phương trình: 2 3x − 5x − 2 = 0 b) Cho phương trình 2
x − x −1 = 0 có 2 nghiệm phân biệt là x1, x2 . Không
giải phương trình, hãy tính giá trị biểu thức: 4 2
A = x − x + x −1 − x 1 1 2 2
Câu 3. (2.0 điểm)
1. Theo Hướng dẫn thi vào lớp 10 THPT năm 2023-2024 của Nghệ An, học
sinh đăng ký dự thi trực tuyến trên Trang web: https://nghean.tsdc.vnedu.vn. Tại hai
trường THPT A và B có tổng số chỉ tiêu tuyển sinh là 950 học sinh. Số lượng thí
sinh đăng kí dự thi trực tuyến vào trường A vượt 18% và vào trường B vượt 20% so
với chỉ tiêu tuyển sinh của mỗi trường nên tổng số thí sinh đăng ký dự thi vượt chỉ
tiêu tuyển sinh của cả hai trường là 181 học sinh. Hỏi chỉ tiêu tuyển sinh của mỗi
trường là bao nhiêu học sinh?
2. Bố bạn Minh thuê thợ đến sơn giả đá 2 cây cột
hình trụ kích thước như nhau với giá 360000đ/m2. Biết rằng
cột cao 3,6m và chu vi của đáy cột bằng 1,5m. Hỏi bố bạn
Minh phải trả bao nhiêu tiền công cho thợ sơn?
Câu 4. (3,0 điểm)
Cho đường tròn tâm O đường kính AB. Một điểm C cố định thuộc đoạn thẳng
AO (C khác A và O). Đường thẳng đi qua C và vuông góc với AO cắt đường tròn đã
cho tại D và K. Trên cung BD nhỏ lấy điểm M (M khác B và D). Tiếp tuyến của
đường tròn đã cho tại M cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và
CD. a) Chứng minh: Tứ giác BCFM nội tiếp. b) Chứng minh: 2 2 2
EF + CD = EC
c) Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh:  +  0 DMI DFM = 90
Câu 5. (0,5 điểm)  2 2  + − −
Giải hệ phương trình sau: x y 7x 3=0  2
y − y( x −1 +1) + x −1 = 0
----------Hết ----------
Họ và tên thí sinh: ……………...............………………… Số báo danh: ……..........…..
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO DIỄN CHÂU
HƯỚNG DẪN CHẤM MÔN TOÁN
ĐỀ THI THỬ VÀO LỚP 10 THPT LẦN 1 NĂM HỌC 2023-2024 Câu Ý Nội dung Điểm
a) Tính giá trị biểu thức: 1012 8 A = 2 3 + − 12 2  3 1  x + 2
b) Rút gọn biểu thức: B = +   :
với x ≥ 0, x ≠ 1.  x −1 x +1 x −1
c) Cho hàm số y = ax + b. Tìm a và b để đồ thị của hàm số song song với
đường thẳng y = -2x + 5 và cắt trục hoành tại điểm có hoành độ bằng 2. 1012 8 0,5 + − = − − a A = 2 3 12 2 3 1012 4 2 3 2 = 2024 0,5
Với x ≥ 0, x ≠ 1, ta có:  3 1  x + 2 0,25 B =  +  : Câu
 ( x +1)( x −1) x +1 x −1 1  3 x −1  x −1 (2,5đ) b =  + . 0,25
( x +1)( x −1) ( x +1)( x −1) x +   2 x + 2 x −1 B = . ( x +1)( x −1) x + 2 0.25 1 = 0.25 x +1 a = 2 −
Đồ thị hàm số song song với đường thẳng y = 2 − x + 5 nên  ta b ≠ 5
có công thức hàm số: y = 2
− x + b (b ≠ 5) c 0.25
Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2 nên thay x
= 2, y = 0 vào công thức hàm số ta được: 0 = 2.2 −
+ b ⇔ b = 4 (TM ) 0,25 Vậy a = 2; − b = 4 a) Giải phương trình: 2 3x − 5x − 2 = 0 b) Cho phương trình 2
x − x −1 = 0 có 2 nghiệm phân biệt là x1, x2 .
Câu Không giải phương trình, hãy tính giá trị biểu thức: 2 4 2
A = x − x + x −1 − x (2,0đ) 1 1 2 2 2 3x − 5x − 2 = 0
a ∆ = (-5)2 -4.3.(-2) =49 > 0 0,5
Phương trình có hai nghiệm phân biệt b − + ∆ 5 + 7 0,5 x − − ∆ − − = = = 2 ; b 5 7 1 x = = = 1 2a 6 2 2a 6 3
Vì phương trình có 2 nghiệm phân biệt x1, x2 nên theo định lí Vi-et ta
có : x + x =1 (1) 1 2  x .x = 1 ( −  2) 0,25 1 2 Từ phương trình : 2 2 4 2
x − x −1 = 0 ⇔ x = x +1 ⇔ x = x + 2x +1
Do x1, x2 là nghiệm nên ta có : 4 2
x = x + 2x +1; 2
x = x = x +1 1 1 1 2 2 2 b Thay vào A ta được: 2 2
A = x + 2x +1− x + x −1 − x +1 = 2x + x − x +1 1 1 1 2 2 1 2 2 = x +1 − x +1 0,25 1 2 2
A = x + x + 2 − 2 (x +1)(x +1) 1 2 1 2 2
A = x + x + 2 − 2 (x x + x x +1) 0.25 1 2 1 2 1 2 2 2 A =1+ 2 − 2 ( 1
− +1+1) ⇔ A =1 ⇔ A = 1 ± 0.25
1. (1,5đ) Theo Hướng dẫn thi vào lớp 10 THPT năm 2023-2024 của Nghệ
An, học sinh đăng ký dự thi trực tuyến trên Trang web:
https://nghean.tsdc.vnedu.vn. Tại hai trường THPT A và B có tổng số chỉ tiêu
tuyển sinh là 950 học sinh. Số lượng thí sinh đăng kí dự thi vào trường A vượt
18% và vào trường B vượt 20% so với chỉ tiêu tuyển sinh của mỗi trường nên tổng
số thí sinh đăng ký dự thi vượt chỉ tiêu tuyển sinh của cả hai trường là 181 học
sinh. Hỏi chỉ tiêu tuyển sinh của mỗi trường là bao nhiêu học sinh?
2. (0,5đ) Bố bạn Minh thuê thợ đến sơn giả đá 2 cây cột hình trụ kích thước
như nhau với giá 360000đ/m2. Biết rằng cột cao 3,6m và chu vi của đáy cột bằng
1,5m. Hỏi bố bạn Minh phải trả bao nhiêu tiền công cho thợ sơn?
Gọi chỉ tiêu tuyển sinh của trường A và trường B lần lượt là x và y
(học sinh) (0 < x, y < 950;x,y∈ N) 0,25 Câu 3
Vì tổng số chỉ tiêu tuyển sinh của hai trường là 950 học sinh nên ta có (1,5đ)
phương trình: x + y = 950 (1) 0,25
Số học sinh dự thi vượt chỉ tiêu của trường A là: 18 x (học sinh) 100
Ý Số học sinh dự thi vượt chỉ tiêu của trường B là: 20 y (học sinh) 0,25 1. 100
Theo bài ra ta có phương trình: 18 20 x +
y =181 ⇔18x + 20y =18100 (2) 0,25 100 100 x + y = 950 18  x +18y = 17100
Từ (1) và (2) ta có hệ:  ⇔ 18  x 20y 18100 18  + =  x + 20y = 18100 2y = 1000 y = 500 ⇔  ⇔  (TM) . x + y = 950 x = 450 0,25
Vậy chỉ tiêu tuyển sinh của trường A và trường B lần lượt là 500 và 450 học sinh. 0,25
Diện tích xung quanh của 2 cây cột là: Ý S = 2.3,6.1,5 = 10,8 (m2) 0,25
2 Số tiền bố bạn Minh phải trả cho thợ là: 10,8.360000 = 3888000(đồng) 0,25
Cho đường tròn tâm O đường kính AB. Một điểm C cố định thuộc đoạn
thẳng AO (C khác A và O). Đường thẳng đi qua C và vuông góc với AO cắt
đường tròn đã cho tại D và K. Trên cung BD nhỏ lấy điểm M (M khác B và D).
Tiếp tuyến của đường tròn đã cho tại M cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và CD.
a) Chứng minh: Tứ giác BCFM nội tiếp. b) Chứng minh: 2 2 2
EF + CD = EC
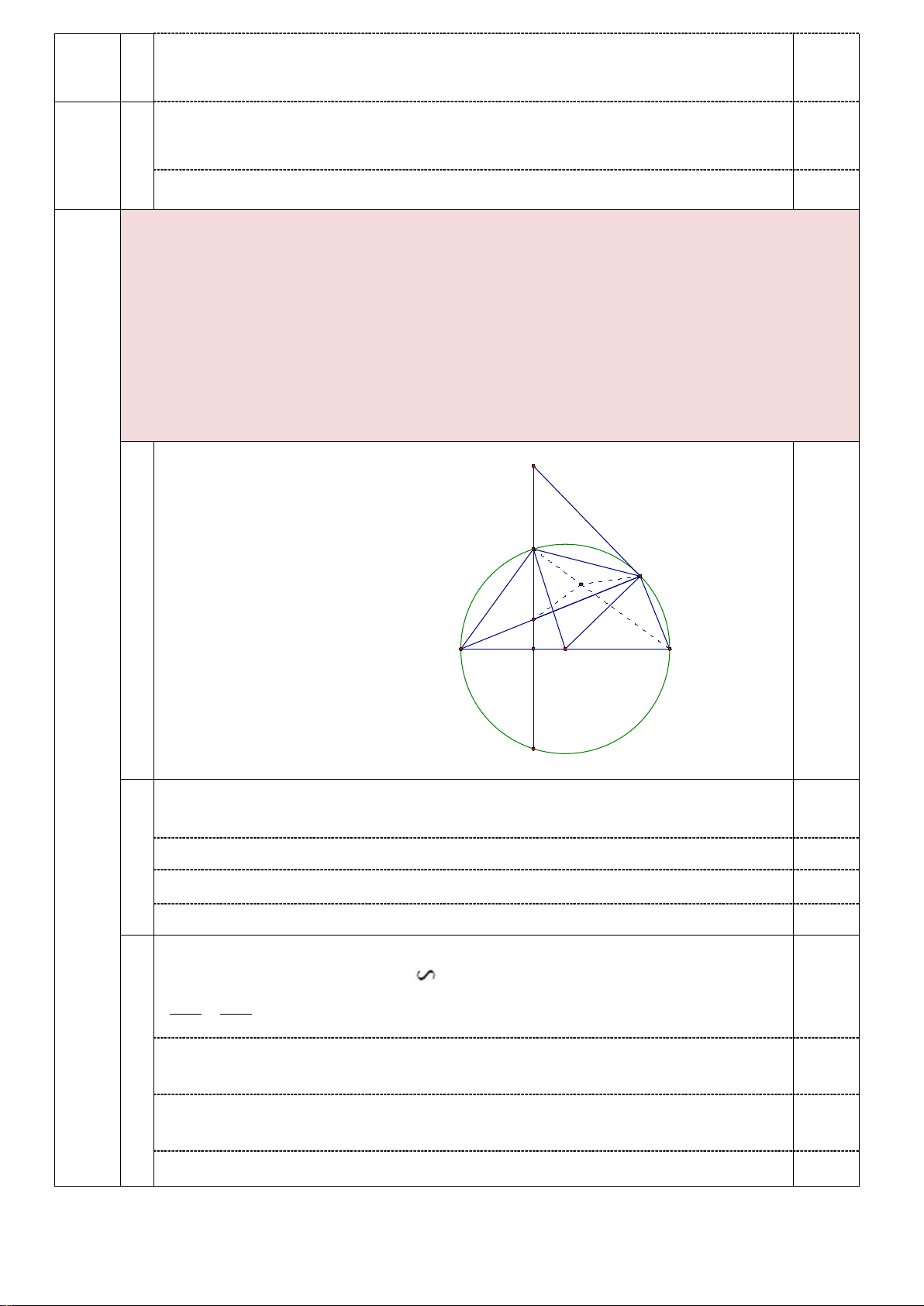
c) Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh:  +  0 DMI DFM = 90 E D Vẽ hình I M đến F câu a) A B 0,5 Câu C O 4 (3,0đ) K Xét tứ giác BCFM có:  0,25 FCB = 90 (Vì CD ⊥ AO ) a 
FMB = 90(góc nội tiếp chắn nửa (O)) 0.25 =>  +    0 FCB FMB = 90 + 90 =180 0.25
=> tứ giác ABOC nội tiếp được đường tròn 0.25
Gọi K là giao điểm thứ hai của CE với đường tròn (O) Ta chứng minh được E ∆ MD E ∆ KM(g.g) nên: EM ED 2 = ⇔ EM = ED.EK 0,25 EK EM
b Vì AO vuông góc DK=>CD = CK Do đó 2 2 2
EM = ED.EK = (EC − CD)(EC + CK) = EC − CD (1) 0,25
Chứng minh được  =  EFM EMF(cùng =  ABM ) 0.25
⇒EFM cân tại E ⇒ EF=EM (2) Từ (1) và (2) 2 2 2 2 2 2
EF = EC − CD ⇔ EF + CD = EC 0,25 Ta có:  
ADC = DBA (cùng phụ với  BAD ). Mà  
DBA = DMA ( góc nt cùng chắn  AD trong (O)) ⇒   ADC = DMA
Xét trong đường tròn ngoại tiếp tam giác DMF ta có:  
DIF = 2DMF (góc ở tâm và góc nội tiếp) ⇒   DIF = 2FDA Mà   0
DIF + 2IDF = 180 (tam giác DIF cân tại I) ⇒   0 2FDA + 2IDF = 180 ⇒   0 FDA + IDF = 90 ⇒ DI ⊥ DA (3) Lại có  0
ADB = 90 (góc nt chắn nửa(O)) ⇒ DB ⊥ DA (4)
Từ (3) và (4) ⇒ Ba điểm D, I, B thẳng hàng. 0,25 ⇒  =  IDM BDM , mà  = 
BDM BAM (2 góc nt cùng chán cung BM)
Ta có DIM cân tại I nên ⇒  =  IDM DMI Suy ra:  =  DMI BAM Ta có:   0
BAM + AFC = 90 (AFC vuông tại C) Mà  = 
AFC DFM (đối đỉnh) nên  +  0 DMI DFM = 90 0,25  2 2  + − −
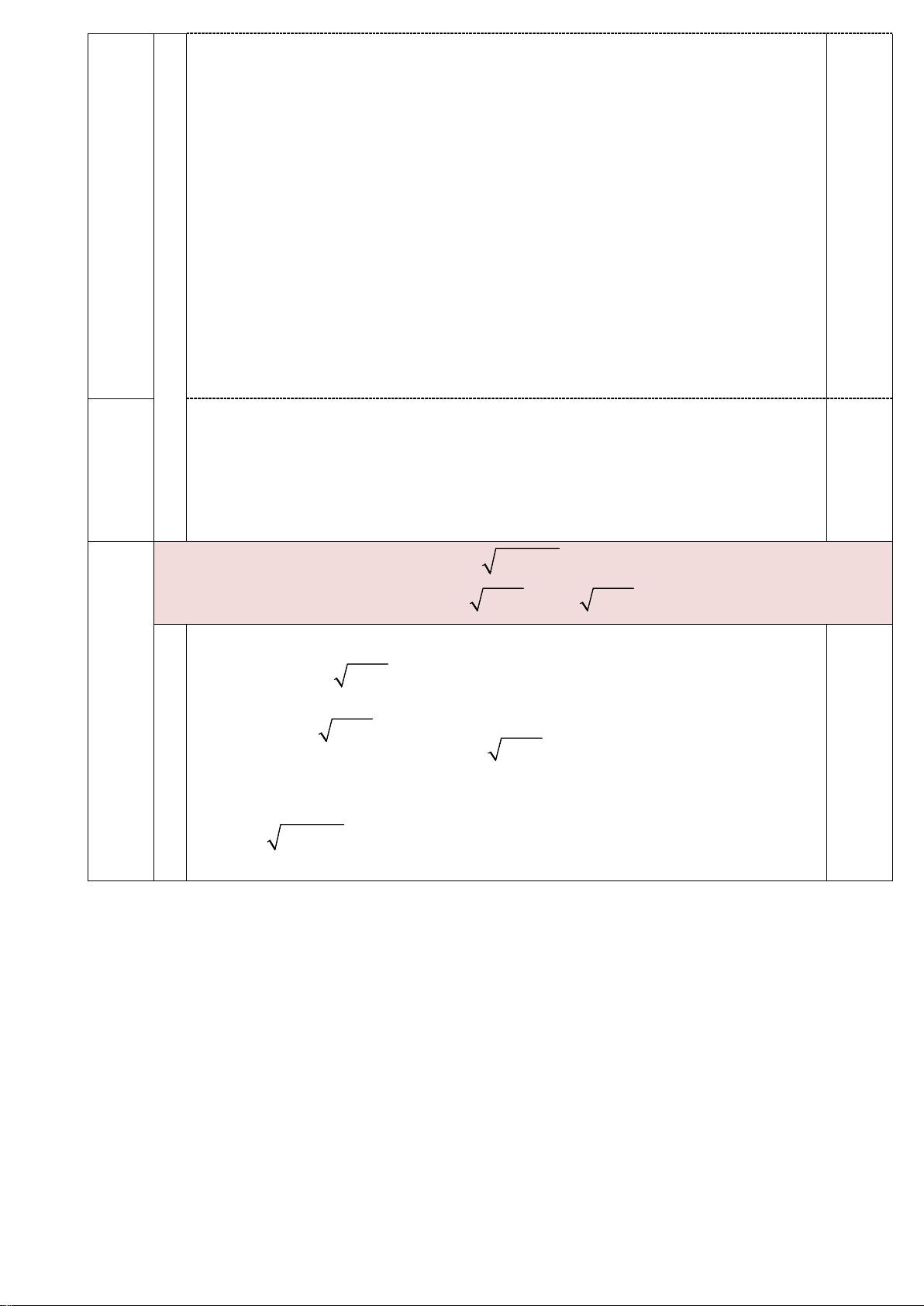
Giải hệ phương trình sau: x y 7x 3=0 (1)  2
y − y( x −1 +1) + x −1 = 0 (2) Điều kiện: x ≥1;y∈R Câu 5 2 (2) y ⇔ − y − x −1(y − ) 1 = 0 0.5đ  y =1
⇔ (y −1)(y − x −1) = 0 ⇔  y = x −1
TH1: y =1thay vào phương trình (1) được: x =1 2 2 4 2
x +1= 7x − 3 ⇔ x − 5x + 4 = 0 ⇔ (do x ≥  1) 0.25 x = 2
TH2: y = x −1 thay vào phương trình (1) được: 2 2 2 2
x + x −1 − 7x − 3 = 0 ⇔ (x − 4) + ( x −1 −1) − ( 7x − 3 − 5) = 0  1 7(x + 2)  ⇔ (x − 2) x + 2 + −  = 0 2  x −1 +1 7x − 3 + 5   2 7x − 3 − 2 1  ⇔ (x − 2)(x + 2) +  = 0 2   7x − 3 + 5 x −1 +1 x = 2 (T / m)  2 ⇔  7x − 3 − 2 1 (x + 2) + = 0  2  7x − 3 + 5 x −1 +1 Với x = 2 ⇒ y =1 2 Với x − − ≥1 thì 7x 3 2 1 (x + 2) + > 0 2 7x − 3 + 5 x −1 +1 0.25
Vậy hệ đã cho có các nghiệm là (x;y) = (1;1);(2;1) Tổng 10,0
Lưu ý: Học sinh giải các cách khác nếu đúng vẫn cho điểm tối đa;
Điểm toàn bài không quy tròn (tính đến 0,25).