Đề thi thử Toán vào 10 lần 2 năm 2023 – 2024 phòng GD&ĐT Giao Thuỷ – Nam Định

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ LẦN 2 TUYỂN SINH LỚP 10 THPT GIAO THỦY NĂM HỌC 2023-2024 Môn: Toán lớp 9 THCS ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút)
Đề thi thử gồm 02 trang.
Phần I - Trắc nghiệm (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm. 2023
Câu 1. Điều kiện để biểu thức có nghĩa là 6  x A. x  6. B. x  6. C. x  6. D. x  6. 2 2
Câu 2. Giá trị biểu thức  5   1  1 5 bằng A.  2 5. B. 4 5. C. 2. D. 2.
Câu 3. Trong các hàm số sau, hàm số nào đồng biến trên ? A. y  4  x  5. B. y   2   1 x 1. C. 2 y  3x . D. 2 y  x .
Câu 4. Cho tam giác ABC vuông tại A , 
ACB  30, cạnh AB  5cm . Độ dài cạnh AC bằng 5 3 5 A. 5 3 c . m B. 5 c . m C. c . m D. c . m 2 3
Câu 5: Phương trình nào sau đây có tổng hai nghiệm bằng 3? A. 2 x  3x  5  0. B. 2 x  3x  2  0. C. 2 x  3x  9  0. D. 2 x  3  0.
Câu 6. Cho hàm số bậc nhất y  1 2m x  m  3. Tìm tất cả các giá trị của tham số m sao cho
đồ thị của hàm số đã cho cắt trục hoành tại điểm có hoành độ bằng 1. 1 A. m  3. B. m  2. C. m  2  . D. m  . 2
Câu 7. Cho tam giác ABC vuông tại , A AB  18cm, AC  24 c .
m Bán kính đường tròn ngoại tiếp tam giác đó bằng A. 30 c . m B. 15c . m C. cm 15 2 c . m D. 20 .
Câu 8. Cho khối nón có đường sinh bằng hai lần bán kính đáy. Biết thể tích của khối nón là 3 3 cm
. Chiều cao của khối nón bằng A. 3 c . m B. 2 3 c . m C. 3 3 c . m D. 3c . m
Phần II - Tự luận (8,0 điểm) Câu 1. (1,5 điểm) 
1) Chứng minh đẳng thức    2 15 5 1 5  20  1  . 3 1  1 x 1 x 1
2) Rút gọn biểu thức A     :  , với x  0, x  1. x  x x 1   x  2 x 1   Trang 1/2 Câu 2. (1,5 điểm)
1) Tìm tọa độ giao điểm của parabol P 2
: y  2x và đường thẳng d  : y  3x –1.
2) Tìm tất cả các giá trị của tham số m để phương trình 2 x  2m   1 x  2m 1  0 có 2
nghiệm phân biệt x , x thỏa mãn 2 x  4x . 1 2 1 2  1 3   4 2x 3  y 1
Câu 3. (1,0 điểm) Giải hệ phương trình  2 1    3. 2x  3 y 1  Câu 4. (3,0 điểm) 1) Cho A
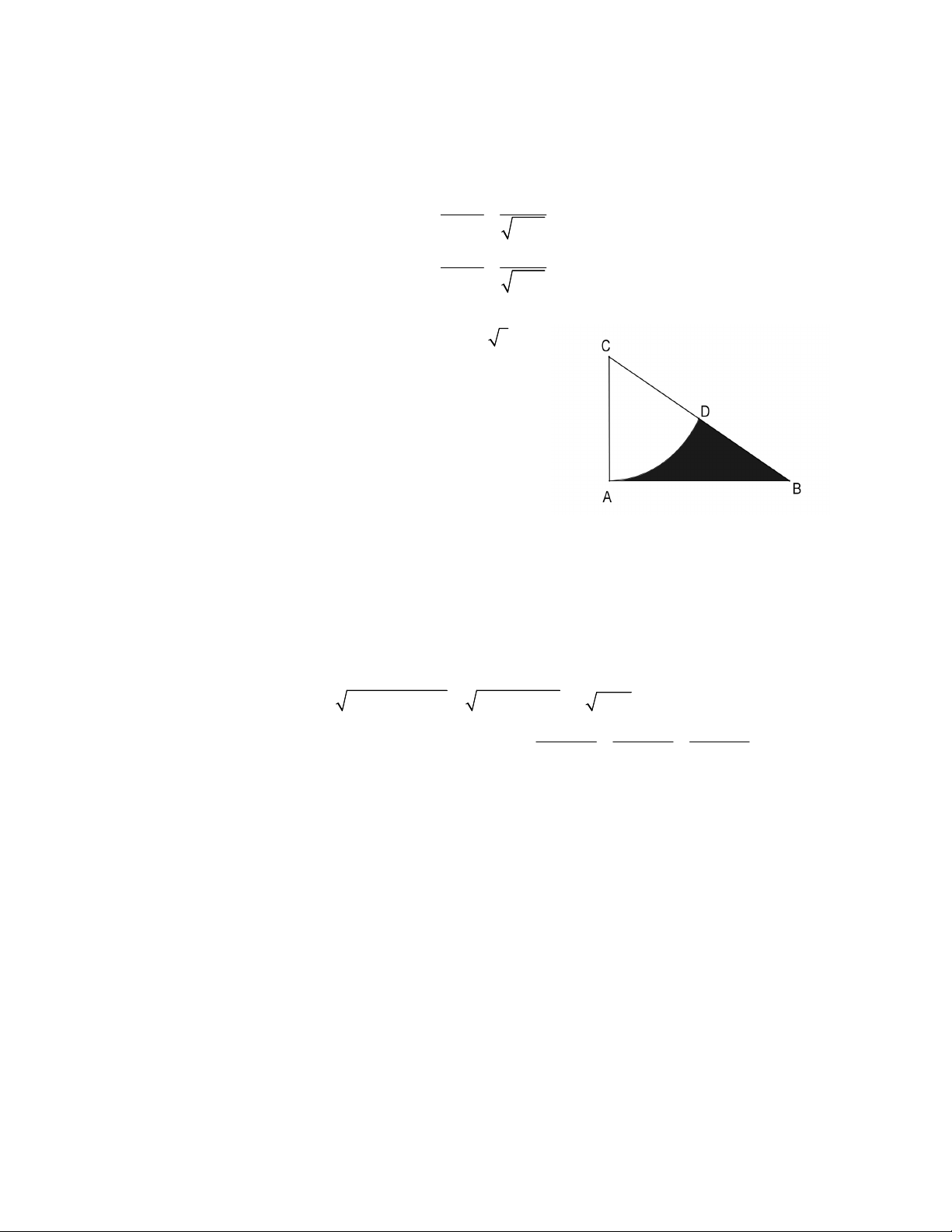
 BC vuông tại A có AB  2 3cm,
AC  2cm. Vẽ cung tròn tâm C bán kính CA cắt BC
tại D. Tính diện tích phần tô đậm trong hình vẽ bên (kết
quả làm tròn đến chữ số thập phân thứ hai).
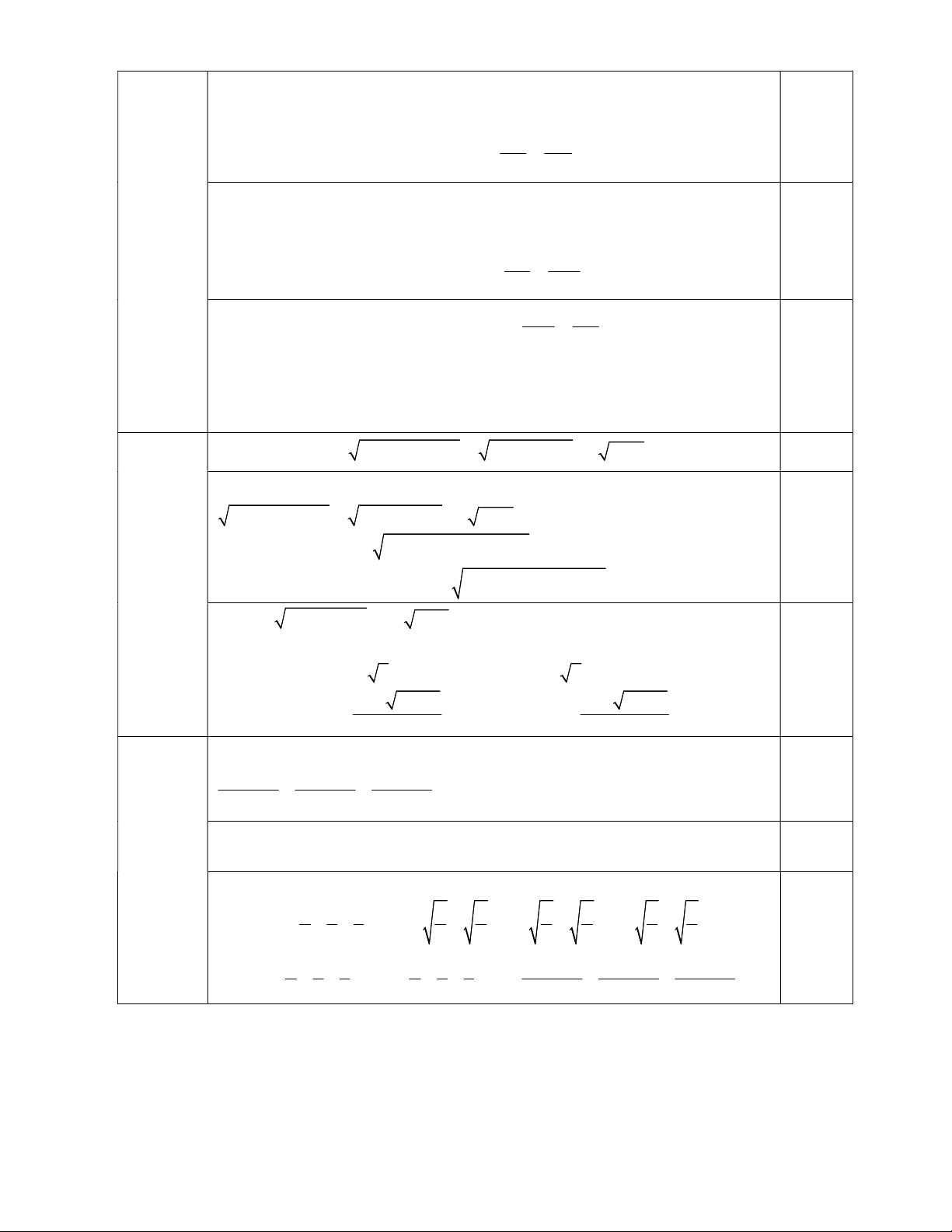
2) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O  AB  AC, các đường cao
BE,CF. Gọi K là giao điểm của đường thẳng EF và BC. Đường thẳng AK cắt đường tròn O tại M ( M khác A ).
a. Chứng minh BFEC là tứ giác nội tiếp.
b. Chứng minh KB.KC  KE.KF và  MAF   MEF. Câu 5. (1,0 điểm) 1. Giải phương trình 2 2
7x  25x 19  x  2x  35  7 x  2 . 1 1 1
2. Xét x, y, z  0 và x  y  z  3 . Chứng minh:    1. 2 2 2 x  2yz y  2zx z  2xy
------------ Hết ------------
Họ và tên thí sinh: ……………………………………
Họ tên, chữ ký GT 1: ……………………………………...
Số báo danh: …………………………………………...
Họ tên, chữ ký GT 2: ……………………………………... Trang 2/2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI THỬ LẦN 2 TUYỂN SINH LỚP 10 THPT GIAO THUỶ NĂM HỌC 2022-2023 HƯỚNG DẪN CHẤM Môn: Toán lớp 9 THCS I. Hướng dẫn chung
1. Học sinh giải theo cách khác mà đúng cho điểm tối đa.
2. Điểm toàn bài là tổng điểm các câu, không làm tròn.
II. Đáp án và thang điểm
Phần I. Trắc nghiệm: (2 điểm) Mỗi câu đúng cho 0,25 điểm Câu Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Đáp án C A B A B C B D
Phần II. Tự luận: (8 điểm) Câu Nội dung Điểm  Chứng minh đẳng thức    2 15 5 1 5  20  1  . 3 1 Câu 1.1 5  3   (0,5 điểm) 1 VT   5 1  2 5 0,25 3 1  5  5 1 2 5  1  . 0,25  1 x 1 x 1
Rút gọn biểu thức A     :  , với x  0, x  1. x  x x 1   x  2 x 1  
Với x  0, x  1 ta có:  1 x 1  x 1 A     :  0,25 x( x 1) ( x 1)( x 1)        x  2 1 Câu 1.2  1 1  x 1 (1,0 điểm)     : 0,25
 x( x 1) ( x 1)   x  2 1  x x   2 1 1  . 0,25 x( x 1) x 1 x 1   x 1
. Vậy với x  0, x  1 thì A  0,25 x x
Tìm tọa độ giao điểm của parabol P 2
: y  2x và đường thẳng d  : y  3x –1. Câu 2.1
Xét phương trình hoành độ giao điểm của (P) và (d): 2 2x  3x –1 (0,5 điểm) 1 0,25
Giải PT tìm được x  1; x  1 2 2 Với x  1; y  2 . 0,25 1 1 Trang 1/4 1 1 Với x   y  . 2 2 2 2
Vậy tọa độ giao điểm của (P) và (d) là 1;2 1 1 ; ( ; ). 2 2
Tìm tất cả các giá trị của tham số m để phương trình 2 x  2m   1 x  2m 1  0
có 2 nghiệm phân biệt x , x thỏa mãn 2 x  4x . 1 2 1 2
Vì phương trình có a  b  c  1 2m  2  2m 1  0
PT luôn có hai nghiệm: x  ;1 x  2m 1 0,25
+)PT (1) có hai nghiệm phân biệt  2m 1  1  m  0 Ta xét 2 trường hợp: TH1: x  ; 1 x  2m 1. Khi đó: 1 2 Câu 2.2 0,25 2 x  4x  12 
m   m    m    m   tm 1 2  4 2  3 (1 điểm) 1 8 4 1 8 3 ( ) 8 TH2: x  2m  ; 1 x  1 1 2  1 m  (tm) 0,25 Khi đó: 2 x  4x  m m 1 2
2  12  .41  2 1  2   2  3 m   (tm)  2  3 1 3 Vậy m   ;  ;
 là các giá trị cần tìm. 0,25  8 2 2  1 3   4 2x 3  y 1
Giải hệ phương trình:  2 1    3. 2x  3 y 1   3 x  Điều kiện  2 y  1. 0,25 1 1 Câu 3 Đặt a  ; b  b  0 2x  3 y 1 (1 điểm) a  3b  4 a 1 Hệ trở thành    tm 0,25 2a  b  3 b  1  1  1 a 1   2x  3 x  2      tm 0,25 b  1 1 y     0 1  y 1 
Vậy hệ phương trình có nghiệm duy nhất 2;0. 0,25 1) Cho  vuông tại A có 
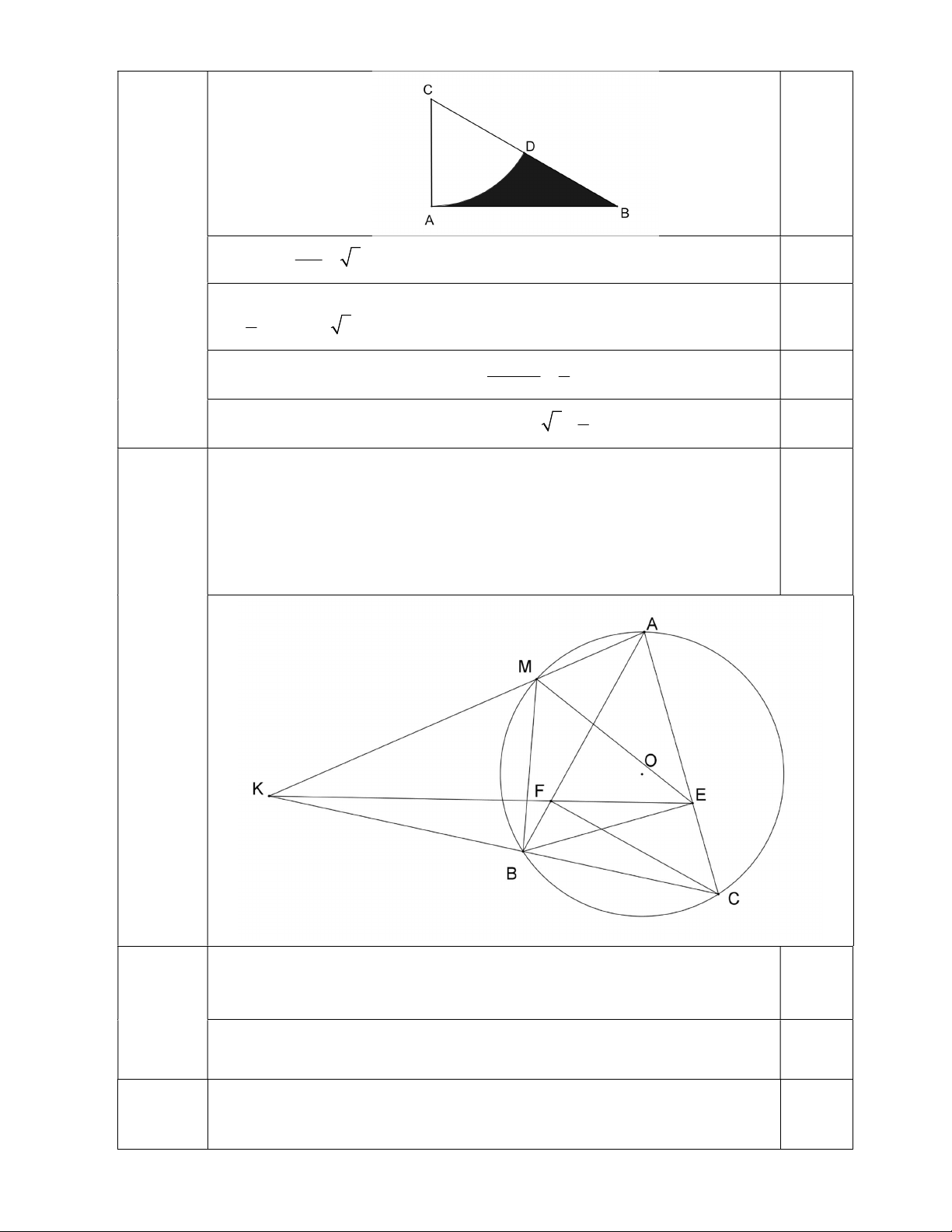
AC  2cm. Vẽ cung tròn tâm C Câu 4.1 ABC AB 2 3cm, (1 điểm)
bán kính CA cắt BC tại D. Tính diện tích phần tô đậm trong hình vẽ bên (kết
quả làm tròn đến chữ số thập phân thứ hai). Trang 2/4 AB tan  ACB 3  ACB 60     0,25 AC
Diện tích tam giác ABC là: 1 0,25 S = AB.AC=2 3  2 cm 1  2 2 .2 .60 2
Diện tích hình quạt tròn CAD là: S     2 cm . 0,25 2  360 3 2
Diện tích phần được tô màu là: S  S  S  2 3   1,37  2 cm 0,25 1 2  3
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O  AB  AC , các
đường cao BE,CF. Gọi K là giao điểm của đường thẳng EF và BC. Đường
thẳng AK cắt đường tròn O tại M ( M khác A ).
a. Chứng minh BFEC là tứ giác nội tiếp. b. Chứng minh K . B KC  KE.KF và  MAF   MEF. Câu 4.2 BE  AC  gt   o BEC  90 ; 0,5 Câu 4.2.a CF  AB  gt   o BFC  90 (1 điểm) Xét tứ giác BCEF có  BEC   o
BFC  90 nên tứ giác BCEF nội tiếp đường tròn 0,5 đường kính BC.
Câu 4.2.b Vì tứ giác BCEF nội tiếp suy ra  AFE   ECK ( cùng bù với  EFB ) 0,25 (1 điểm) Mà  AFE  
KFB (đối đỉnh) do đó  KFB   ECK Trang 3/4 Xét hai tam giác K  BF và K  EC có  KFB   ECK (chứng minh trên);  EKC chung 0,25 KB KF Suy ra K  BF đồng dạng với K  EC    K . B KC  KE.KF   1 KE KC
Xét hai tam giác KBM và K  AC có  MBK   KAC (cùng bù với  MBC ) và  MKB   AKC 0,25 KB KM
Suy ra KBM đồng dạng với K  AC    K . B KC  KM.KA 2 KA KC KM KE Từ  
1 và 2 suy ra KM.KA  KE.KF   3 KF KA Ta lại có  MKE   AKF 4 0,25
Từ 3 và 4 suy ra KME đồng dạng K  FA . Suy ra  MAF   MEF. Giải phương trình 2 2
7x  25x 19  x  2x  35  7 x  2 . Điều kiện x  7. 2 2
7x  25x 19  x  2x  35  7 x  2 0,25 2
 3x 11x  22  7 x  2 x  5 x  7 Câu 5.1   2
x  x     x    x   2 3 5 14 4 5 7 5 x  5x 14 (0,5 điểm) Đặt 2
a  x  5x 14 ;b  x  5 a  0,b  0 . Khi đó phương trình trở thành 2 2
3a  4b  7ab  a  b  3a  4b
Với a  b  x  3  2 7 (thỏa mãn) và x  3  2 7 (loại) 0,25 61 11137 61 11137 Với 3a  4b  x  (thỏa mãn) và x  (loại) 18 18 Xét x, y, z  0 và x  y  z  3 . Chứng minh: 1 1 1    1. 2 2 2 x  2yz y  2zx z  2xy Đặt 2 2 2 x  2yz  ; a y  2zx  ; b z  2xy  c 2 0,25
 a  b  c  (x  y  z)  9 và Câu 5.2 a  0;b  0;c  0 (0,5 điểm) Xét 2 2 2     1 1 1   a b   a c   b c  a b c    9                9 a b c  b a   c a   c b          0,25  1 1 1  1 1 1 1 1 1  9    9     1    1   2 2 2  a b c  a b c x  2 yz y  2zx z  2xy
---------------------------Hết------------------------------ Trang 4/4