Đề thi thử Toán vào 10 năm 2023 – 2024 trường THCS Nguyễn Hữu Thái – Hà Tĩnh

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi thử môn Toán tuyển sinh vào lớp 10 THPT năm học 2023 – 2024 trường THCS Nguyễn Hữu Thái, tỉnh Hà Tĩnh; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

53 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

8 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
Câu 1. (2,0 điểm) Rút gọn cc biểu thức sau:
a)
2 48 3 12 3A
b)
1 1 1
:
11
x
B
x x x x




với
1;0 xx
Câu 2. (3,0 điểm)
a) Giải hệ phương trình sau:
31
28
xy
xy

b) Trong mp toạ độ Oxy, tìm m để đường thẳng (d):
2
y m 1 x 1()
song song với
đường thẳng
d y 3x m 1( ):
.
c) Cho phương trình: x
2
– 5x + m = 0 (m là tham số). Tìm m để phương trình trên
có hai nghiệm x
1
, x
2
thỏa mãn:
12
x x 3
.
Câu 3. (1,0 điểm) Thng giêng hai tổ sản xuất được 900 chi tiết my; thng hai do cải
tiến kỹ thuật tổ I vượt mức 15% và tổ II vượt mức 10% so với thng giêng, vì vậy hai tổ
đã sản xuất được 1010 chi tiết my. Hỏi thng giêng mỗi tổ sản xuất được bao nhiêu chi
tiết my?
Câu 4. (1,0 điểm) Cho tam gic ABC vuông tại A có đường cao AH (H thuộc BC),
biết
0
ACB 60
,
CH = 2 cm
. Tính AB và AC.
Câu 5. (2,0 điểm)Từ điểm A nằm ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC với
đường tròn (B, C là các tiếp điểm). M là điểm bất kì trên cung nhỏ BC (M
B, M
C).
Gọi D, E , F tương ứng là hình chiếu vuông góc của M trên cc đường thẳng AB, AC,
BC.
a) Chứng minh tứ gic MECF là tứ gic nội tiếp.
b) Chứng minh DF là tiếp tuyến của đường tròn đường kính MC.
Câu 6. (1,0 điểm) Cho a, b, c là cc số thc dương thoã mãn : a + b + c = 3 .
Tìm gi trị nhỏ nhất của biểu thức :
2022
1 1 1
b a c b a c
P
b c a
ab bc ac

------------------------ HẾT -----------------------------
Giám thị không giải thích gì thêm
Họ và tên thí sinh ............................................................... Số báo danh ...........................
TRƯỜNG THCS
NGUYỄN HỮU THÁI
ĐỀ THI THỬ TS VÀO THPT NĂM HỌC 2023-2024
Môn Thi: Toán 9
Thời gian làm bài: 90 phút
ĐỀ 01
HƯỚNG DẪN CHẤM ĐỀ THI THỬ TOÁN 9
NĂM HỌC 2022 – 2023 (MĐ 01)
Câu
Nội dung
Điểm
Câu 1
(2,0 đ)
a)
2 48 3 12 3 8 3 6 3 3 3 3A
1,0
b) với
1;0 xx
, ta có:
1 1 1 1 1 1
::
1 1 1 1
1
1 1 1 1 1 1 1
: : .
1 1 1
1 1 1 1
xx
B
x x x x x x
xx
x x x x x x
x x x x
x x x x x x x x












0,5
0,5
Câu 2
(3,0 đ)
a)
3 1 1 3 1 3
2 8 2(1 3 ) 8 2
x y y x y x
x y x x x

2
5
x
y

Vậy hệ phương trình có nghiệm duy nhất (x;y) = (2; -5)
0,75
0,25
b) Đường thẳng d và
d
song song với nhau khi và chỉ khi:
22
m2
m 1 3 m 4
m2
m2
m 1 1 m 2



1,0
c) Ta có: ∆ = 25 – 4.m
Để phương trình đã cho có nghiệm thì ∆
0
25
m
4

(*)
0,25
Theo hệ thức Vi-ét, ta có x
1
+ x
2
= 5 (1); x
1
x
2
= m (2).
0,25
Mặt khc theo bài ra thì
12
x x 3
(3). Từ (1) và (3) suy ra x
1
= 4; x
2
= 1 hoặc x
1
= 1;
x
2
= 4 (4)
0,25
Từ (2) và (4) suy ra: m = 4. Thử lại thì thoả mãn.
0,25
Câu 4
(1,0 đ)
Gọi x, y số chi tiết my của tổ 1, tổ 2 sản xuất trong thng giêng (x, y
N
*
),
0,25
ta có x + y = 900 (1) (vì thng giêng 2 tổ sản xuất được 900 chi tiết). Do cải tiến kỹ thuật
nên thng hai tổ 1 sản xuất được: x + 15%x, tổ 2 sản xuất được: y + 10%y.
Cả hai tổ sản xuất được: 1,15x + 1,10y = 1010 (2)
0,25
Từ (1), (2) ta có hệ phương trình:
x y 900 1,1x 1,1y 990 0,05x 20
1,15x 1,1y 1010 1,15x 1,1y 1010 x y 900




<=> x = 400 và y = 500 (thoả mãn)
0,25
Vậy trong thng giêng tổ 1 sản xuất được 400 chi tiết my, tổ 2 sản xuất được 500 chi
tiết my.
0,25
Câu 4
(1,0 đ)
Đặt CH = a
ACH
có:
CH
cosC
AC
nên
0
CH a a
AC 2a = 2.2 = 4
1
cosC cos60
2
(cm) (0,5đ)
0,5
ABC
có
0
AB = AC.tanC = 2a.tan60 2a. 3 2.2 3 4 3
(cm) (0,5đ)
Vậy
AB = 4 3( )cm
,
AC 4( )cm
.
0,5
Câu 5
(2,0 đ)
a) Tứ gic MECF có:
(gt)
Do đó tứ gic MECF nội tiếp đường tròn
đường kính MC
1,0
b) Gọi I là trung điểm của MC, Do tứ gic MECF nội tiếp đường tròn đường kính
MC nên IF = IM =>
0,25
AB là tiếp tuyến của đường tròn (O) nên (Góc nội tiếp và góc
tạo bởi tiếp tuyến và dây cung cùng chắn cung BM)
Chứng minh tương t câu a ta có tứ gic MFBD là tứ gic nội tiếp. Do đó
( Hai góc nội tiếp cùng chắn cung DM)
0,25
Từ (2) và (3) suy ra:
0,25
Từ (1) và (4) suy ra ( Tam giác MFC vuông
tại F).
Do đó IF vuông góc với FD, Hay DF là tiếp tuyến của đường tròn đường kính
MC.
0,25
Câu 6
(1,0 đ)
Ta có:
bca
acb
cba
cba
3
3
3
3
Vì a,b,c dương nên :
2
3
232
c
ababcabba
Tương t ta có:
2
3
;
2
3 b
ac
a
bc
Suy ra:
3
2
39
2
)(9
cba
cabcab
0,5
Ta có:
2
2
1
;
2
2
1
;
2
2
1
ac
a
ca
a
cabc
c
bc
c
bcab
b
ab
b
ab
0,25
M
I
O
F
E
D
C
B
A
Suy ra:
2
3
2111
acbcab
a
ca
c
bc
b
ab
Vậy :
2022 3 1345
3 2 2
P
Dấu (=) xẩy ra khi và chỉ khi : a = b = c = 1
0,25
Ghi chú: HS làm đúng các cách cho điểm tối đa.
Câu 1. (2,0 điểm) Rút gọn cc biểu thức sau:
a)
2 45 2 20 5A
b)
1 1 1
:
11
x
B
x x x x




với
1;0 xx
Câu 2. (3,0 điểm)
a) Giải hệ phương trình sau:
23
35
xy
xy


b) Trong mp toạ độ Oxy, tìm m để đường thẳng (d): y = (m
2
+1)x -1 song với
đường thẳng (d’): y= 5x + m + 1
c) Cho phương trình: x
2
– 5x + m = 0 (m là tham số). Tìm m để phương trình trên
có hai nghiệm x
1
, x
2
thỏa mãn:
1
21
xx
Câu 3. (1,0 điểm) Thng giêng hai tổ sản xuất được 1000 chi tiết my; thng hai do cải
tiến kỹ thuật tổ I vượt mức 15% và tổ II vượt mức 10% so với thng giêng, vì vậy hai tổ
đã sản xuất được 1120 chi tiết my. Hỏi thng giêng mỗi tổ sản xuất được bao nhiêu chi
tiết my?
Câu 4. (1,0 điểm) Cho tam gic ABC vuông tại A có đường cao AH (H thuộc BC). Biết
AC = 6 cm và = 30
0
. Tính độ dài đoạn thẳng BC và diện tích tam gic AHB.
Câu 5. (2,0 điểm) Từ điểm S nằm ngoài đường tròn (O), kẻ hai tiếp tuyến SA, SB với
đường tròn (A, B là cc tiếp điểm). M là điểm bất kì trên cung nhỏ AB (M
A, M
B).
Gọi D, E , F tương ứng là hình chiếu vuông góc của M trên cc đường thẳng SA, SB,
AB.
a) Chứng minh tứ gic MEBF là cc tứ gic nội tiếp.
b) Chứng minh DF là tiếp tuyến của đường tròn đường kính MB.
Câu 6. (1,0 điểm) Cho a, b, c là cc số thc dương thoã mãn : a + b + c = 3 .
Tìm gi trị nhỏ nhất của biểu thức :
2022
1 1 1
b a c b a c
P
b c a
ab bc ac

------------------------ HẾT -----------------------------
Giám thị không giải thích gì thêm
Họ và tên thí sinh ............................................................... Số báo danh ...........................
TRƯỜNG THCS
NGUYỄN HỮU THÁI
ĐỀ THI THỬ TS VÀO THPT NĂM HỌC 2023-2024
Môn Thi: Toán 9
Thời gian làm bài: 90 phút
ĐỀ 02
HƯỚNG DẪN CHẤM ĐỀ THI THỬ TOÁN 9
NĂM HỌC 2022 – 2023 (MĐ 02)
Câu
Nội dung
Điểm
Câu 1
(2,0 đ)
a)
2 45 2 20 5 6 5 4 5 5 3 5AA
1,0
b) với
1;0 xx
, ta có:
1 1 1 1 1 1
::
1 1 1 1
1
1 1 1 1 1 1 1
: : .
1 1 1
1 1 1 1
xx
BB
x x x x x x
xx
x x x x x x
x x x x
x x x x x x x x












0,5
0,5
Câu 2
(3,0 đ)
a)
2 3 3 2 3 2 1
3 5 3(3 2 ) 5 7 14 2
x y y x y x y
x y x x x x
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (-1; 2)
0,75
0,25
b) Đường thẳng d và
d
song song với nhau khi và chỉ khi:
2
2
2
2
4
11
51
22
m
m
m
m
m
m
m
1,0
) Cho phương trình: x
2
– 5x + m = 0 (m là tham số). Tìm m để phương trình
trên có hai nghiệm x
1
, x
2
thỏa mãn:
1
21
xx
c) Ta có: ∆ = 25 – 4.m
Để phương trình đã cho có nghiệm thì ∆
0
25
m
4

(*)
0,25
Theo hệ thức Vi-ét, ta có x
1
+ x
2
= 5 (1); x
1
x
2
= m (2).
0,25
Mặt khc theo bài ra thì
1
21
xx
(3). Từ (1) và (3) suy ra x
1
= 2; x
2
= 3 hoặc x
1
= 3;
x
2
= 2 (4)
0,25
Từ (2) và (4) suy ra: m = 6. Thử lại thì thoả mãn.
0,25
Câu 4
(1,0 đ)
Gọi x, y số chi tiết my của tổ 1, tổ 2 sản xuất trong thng giêng (x, y
N
*
),
0,25
ta có x + y = 1000 (1) (vì thng giêng 2 tổ sản xuất được 1000 chi tiết). Do cải tiến kỹ
thuật nên thng hai tổ 1 sản xuất được: x + 15%x, tổ 2 sản xuất được: y + 10%y.
Cả hai tổ sản xuất được: 1,15x + 1,10y = 1120 (2)
0,25
Từ (1), (2) ta có hệ phương trình:
600
400
1000
20,05.0
11201.115,1
11001,1,1.1
11201.115,1
1000
y
x
yx
x
yx
yx
yx
yx
<=> x = 400 và y = 500 (thoả mãn)
0,25
Vậy trong thng giêng tổ 1 sản xuất được 400 chi tiết my, tổ 2 sản xuất được 600 chi
tiết my.
0,25
Câu 4
(1,0 đ)
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Biết AC = 6 cm và
= 30
0
. Tính độ dài đoạn thẳng BC và diện tích tam giác AHB.
Theo tỉ số lượng gic góc nhọn ta có
0
6
sin 12
sin sin30
AC AC
B BC BC
BC C
Vậy BC = 12 cm
0,5
Áp dụng hệ thức cạnh và góc trong tam gic vuông ABC, ta có:
+
22
2
6
.3
12
12 3 9
AC
AC BC CH CH
BC
BH BC CH BH BH cm
+
22
. 9.3 3 3AH BH CH AH AH
cm
0,25
Diện tích tam gic AHB là:
1 1 27. 3
. . .9.3 3
2 2 2
AHB
S AH BH
cm
2
0,25
Câu 5
(2,0 đ)
a) Tứ gic MEBF có:
(gt)
Do đó tứ gic MEBF nội tiếp đường tròn đường
kính MB
1,0
b) Gọi I là trung điểm của MB, Do tứ gic MEBF nội tiếp đường tròn đường kính
MC nên IF = IM =>
0,25
SA là tiếp tuyến của đường tròn (O) nên (Góc nội tiếp và góc tạo
bởi tiếp tuyến và dây cung cùng chắn cung AM)
Chứng minh tương t câu a ta có tứ gic MFAD là tứ gic nội tiếp. Do đó
( Hai góc nội tiếp cùng chắn cung DM)
0,25
Từ (2) và (3) suy ra:
0,25
Từ (1) và (4) suy ra ( Tam giác MFC vuông
tại F).
Do đó IF vuông góc với FD, Hay DF là tiếp tuyến của đường tròn đường kính
MB.
0,25
Câu 6
(1,0 đ)
Ta có:
bca
acb
cba
cba
3
3
3
3
Vì a,b,c dương nên :
2
3
232
c
ababcabba
Tương t ta có:
2
3
;
2
3 b
ac
a
bc
Suy ra:
3
2
39
2
)(9
cba
cabcab
0,5
H
B
C
A
M
I
O
F
E
D
B
A
S
Ta có:
2
2
1
;
2
2
1
;
2
2
1
ac
a
ca
a
cabc
c
bc
c
bcab
b
ab
b
ab
Suy ra:
2
3
2111
acbcab
a
ca
c
bc
b
ab
0,25
Vậy :
2022 3 1345
3 2 2
P
Dấu (=) xẩy ra khi và chỉ khi : a = b = c = 1
0,25
Ghi chú: HS làm đúng các cách cho điểm tối đa.
| 1/8
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THCS
ĐỀ THI THỬ TS VÀO THPT NĂM HỌC 2023-2024 NGUYỄN HỮU THÁI Môn Thi: Toán 9
Thời gian làm bài: 90 phút ĐỀ 01
Câu 1. (2,0 điểm) Rút gọn các biểu thức sau:
a) A  2 48  3 12  3  1 1  x 1 b) B   :   với x  ; 0 x  1  x x x 1 x 1
Câu 2. (3,0 điểm)
3x y  1
a) Giải hệ phương trình sau: 
x  2y  8
b) Trong mp toạ độ Oxy, tìm m để đường thẳng (d): 2
y  (m 1)x 1 song song với
đường thẳng (d ) : y  3x  m 1.
c) Cho phương trình: x2 – 5x + m = 0 (m là tham số). Tìm m để phương trình trên có hai nghiệm x   1, x2 thỏa mãn: x x 3 . 1 2
Câu 3. (1,0 điểm) Tháng giêng hai tổ sản xuất được 900 chi tiết máy; tháng hai do cải
tiến kỹ thuật tổ I vượt mức 15% và tổ II vượt mức 10% so với tháng giêng, vì vậy hai tổ
đã sản xuất được 1010 chi tiết máy. Hỏi tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy?
Câu 4. (1,0 điểm) Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC), biết 0
ACB  60 , CH = 2 cm . Tính AB và AC.
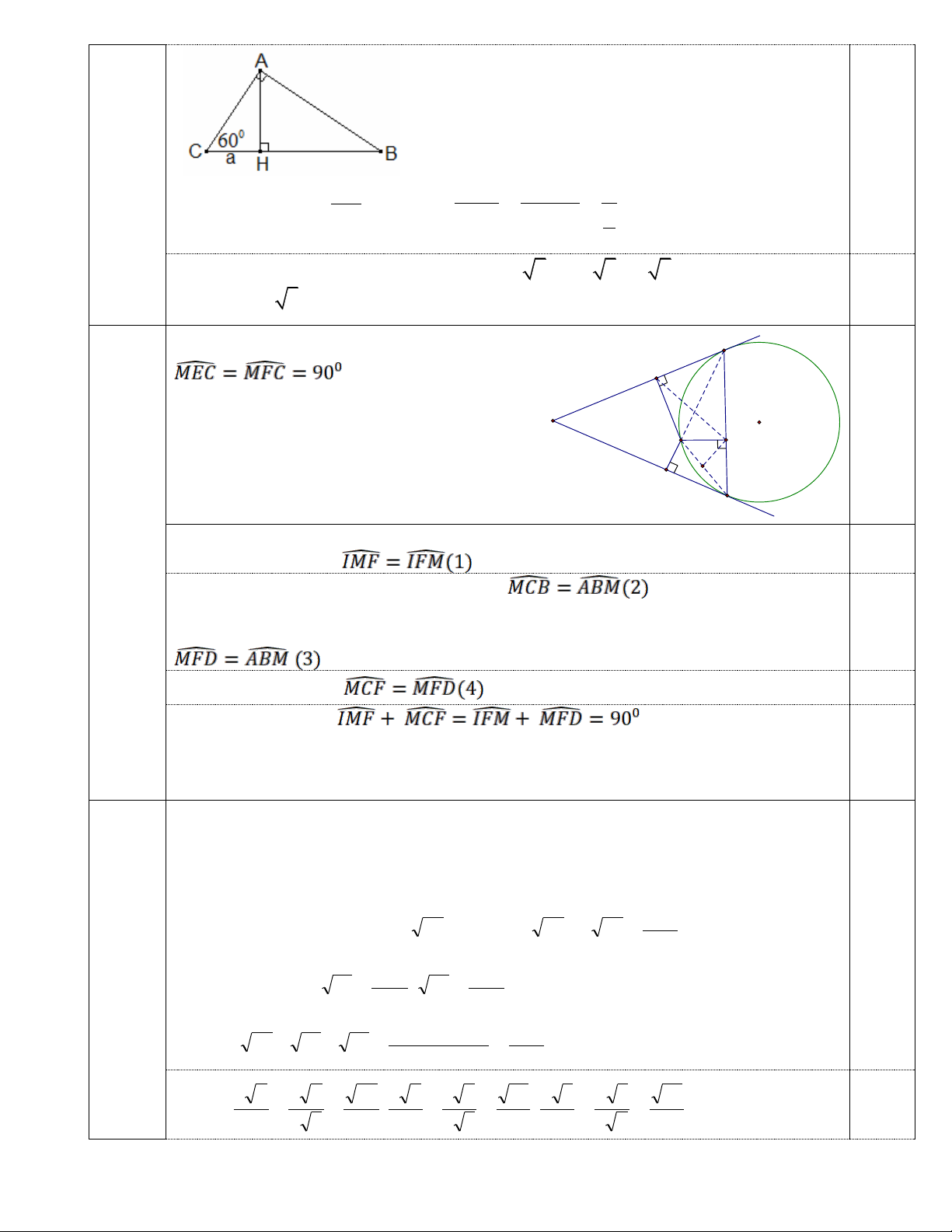
Câu 5. (2,0 điểm)Từ điểm A nằm ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC với
đường tròn (B, C là các tiếp điểm). M là điểm bất kì trên cung nhỏ BC (M  B, M  C).
Gọi D, E , F tương ứng là hình chiếu vuông góc của M trên các đường thẳng AB, AC, BC.
a) Chứng minh tứ giác MECF là tứ giác nội tiếp.
b) Chứng minh DF là tiếp tuyến của đường tròn đường kính MC.
Câu 6. (1,0 điểm) Cho a, b, c là các số thực dương thoã mãn : a + b + c = 3 . Tìm giá trị nhỏ 2022 b a c b a c
nhất của biểu thức : P    
ab bc ac 1 b 1 c 1 a
------------------------ HẾT -----------------------------
Giám thị không giải thích gì thêm
Họ và tên thí sinh ............................................................... Số báo danh ...........................
HƯỚNG DẪN CHẤM ĐỀ THI THỬ TOÁN 9
NĂM HỌC 2022 – 2023 (MĐ 01) Câu Nội dung Điểm
a) A  2 48  3 12  3  8 3  6 3  3  3 3 1,0 b) với x  ; 0 x  1, ta có:    1 1  x 1 1 1 x 1   0,5 Câu 1 B   :   :            (2,0 đ) x x x 1 x 1 x   x   1 x 1 x 1    1 x x 1 x 1 x 1 x 1 x 1 1       0,5
x x  1 x x   : 1  x
x x   : 1 x x x    . 1 1 1 x 1 x
 3x y 1 y 13xy 13xx  2 0,75 a)       
x  2y  8 
x  2(13x)  8  x  2  y  5 Vậy hệ phương
trình có nghiệm duy nhất (x;y) = (2; -5) 0,25
b) Đường thẳng d và d song song với nhau khi và chỉ khi: 2 2 m 1  3 m  4 m  2        1,0 m  2  m 1  1 m  2 m  2 Câu 2
(3,0 đ) c) Ta có: ∆ = 25 – 4.m 25 0,25
Để phương trình đã cho có nghiệm thì ∆  0  m  (*) 4
Theo hệ thức Vi-ét, ta có x1 + x2 = 5 (1); x1x2 = m (2). 0,25
Mặt khác theo bài ra thì x  x  3 (3). Từ (1) và (3) suy ra x 1 2 1 = 4; x2 = 1 hoặc x1 = 1; 0,25 x2 = 4 (4)
Từ (2) và (4) suy ra: m = 4. Thử lại thì thoả mãn. 0,25
Gọi x, y số chi tiết máy của tổ 1, tổ 2 sản xuất trong tháng giêng (x, y  N* ), 0,25
ta có x + y = 900 (1) (vì tháng giêng 2 tổ sản xuất được 900 chi tiết). Do cải tiến kỹ thuật
nên tháng hai tổ 1 sản xuất được: x + 15%x, tổ 2 sản xuất được: y + 10%y. 0,25
Cả hai tổ sản xuất được: 1,15x + 1,10y = 1010 (2) Từ (1) Câu 4
, (2) ta có hệ phương trình:
(1,0 đ) x  y  900 1  ,1x 1,1y  990 0  ,05x  20      0,25 1  ,15x 1,1y 1010 1  ,15x 1,1y 1010 x  y  900
<=> x = 400 và y = 500 (thoả mãn)
Vậy trong tháng giêng tổ 1 sản xuất được 400 chi tiết máy, tổ 2 sản xuất được 500 chi tiết máy. 0,25 Đặt CH = a Câu 4 (1,0 đ) CH CH a a A  CHcó: cosC  nên AC   
 2a = 2.2 = 4(cm) (0,5đ) AC 0 cos C cos 60 1 0,5 2 A  BCcó 0
AB = AC.tanC = 2a.tan 60  2a. 3  2.2 3  4 3 (cm) (0,5đ) Vậy 0,5 AB = 4 3( ) cm , AC  4( ) cm . a) Tứ giác MECF có: B (gt) D
Do đó tứ giác MECF nội tiếp đường tròn A đường kính MC O 1,0 M F I E C Câu 5
b) Gọi I là trung điểm của MC, Do tứ giác MECF nội tiếp đường tròn đường kính 0,25
(2,0 đ) MC nên IF = IM =>
AB là tiếp tuyến của đường tròn (O) nên (Góc nội tiếp và góc
tạo bởi tiếp tuyến và dây cung cùng chắn cung BM)
Chứng minh tương tự câu a ta có tứ giác MFBD là tứ giác nội tiếp. Do đó 0,25
( Hai góc nội tiếp cùng chắn cung DM) Từ (2) và (3) suy ra: 0,25 Từ (1) và (4) suy ra ( Tam giác MFC vuông tại F).
Do đó IF vuông góc với FD, Hay DF là tiếp tuyến của đường tròn đường kính 0,25 MC.
a b  3 c
Ta có: a b c  3  b c  3  a
a c  3 b  Vì a,b,c dương nên : 3 c
a b  2 ab  3  c  2 ab ab  0,5 Câu 6 2 (1,0 đ)   Tương tự ta có: 3 a 3 b   bc ; ac 2 2
9  (a b c) 9  3
Suy ra: ab bc ca    3 2 2 b a b a ab c b c b bc a c a c ac Ta có:   ;   ;   0,25 1 b 2 b 2 1 c 2 c 2 1 a 2 a 2 b a c b a c
ab bc ac 3 Suy ra:     1 b 1 c 1 a 2 2 Vậy : 2022 3 1345 P    3 2 2 0,25
Dấu (=) xẩy ra khi và chỉ khi : a = b = c = 1
Ghi chú: HS làm đúng các cách cho điểm tối đa. TRƯỜNG THCS
ĐỀ THI THỬ TS VÀO THPT NĂM HỌC 2023-2024 NGUYỄN HỮU THÁI Môn Thi: Toán 9
Thời gian làm bài: 90 phút ĐỀ 02
Câu 1. (2,0 điểm) Rút gọn các biểu thức sau:
a) A  2 45  2 20  5  1 1  x 1 b) B   :   với x  ; 0 x  1
x 1 x x x 1
Câu 2. (3,0 điểm)   
a) Giải hệ phương trình sau: 2x y 3 
x  3y  5
b) Trong mp toạ độ Oxy, tìm m để đường thẳng (d): y = (m2 +1)x -1 song với
đường thẳng (d’): y= 5x + m + 1
c) Cho phương trình: x2 – 5x + m = 0 (m là tham số). Tìm m để phương trình trên có hai nghiệm x x x  1, x2 thỏa mãn: 1 1 2
Câu 3. (1,0 điểm) Tháng giêng hai tổ sản xuất được 1000 chi tiết máy; tháng hai do cải
tiến kỹ thuật tổ I vượt mức 15% và tổ II vượt mức 10% so với tháng giêng, vì vậy hai tổ
đã sản xuất được 1120 chi tiết máy. Hỏi tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy?
Câu 4. (1,0 điểm) Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Biết AC = 6 cm và
= 300 . Tính độ dài đoạn thẳng BC và diện tích tam giác AHB.
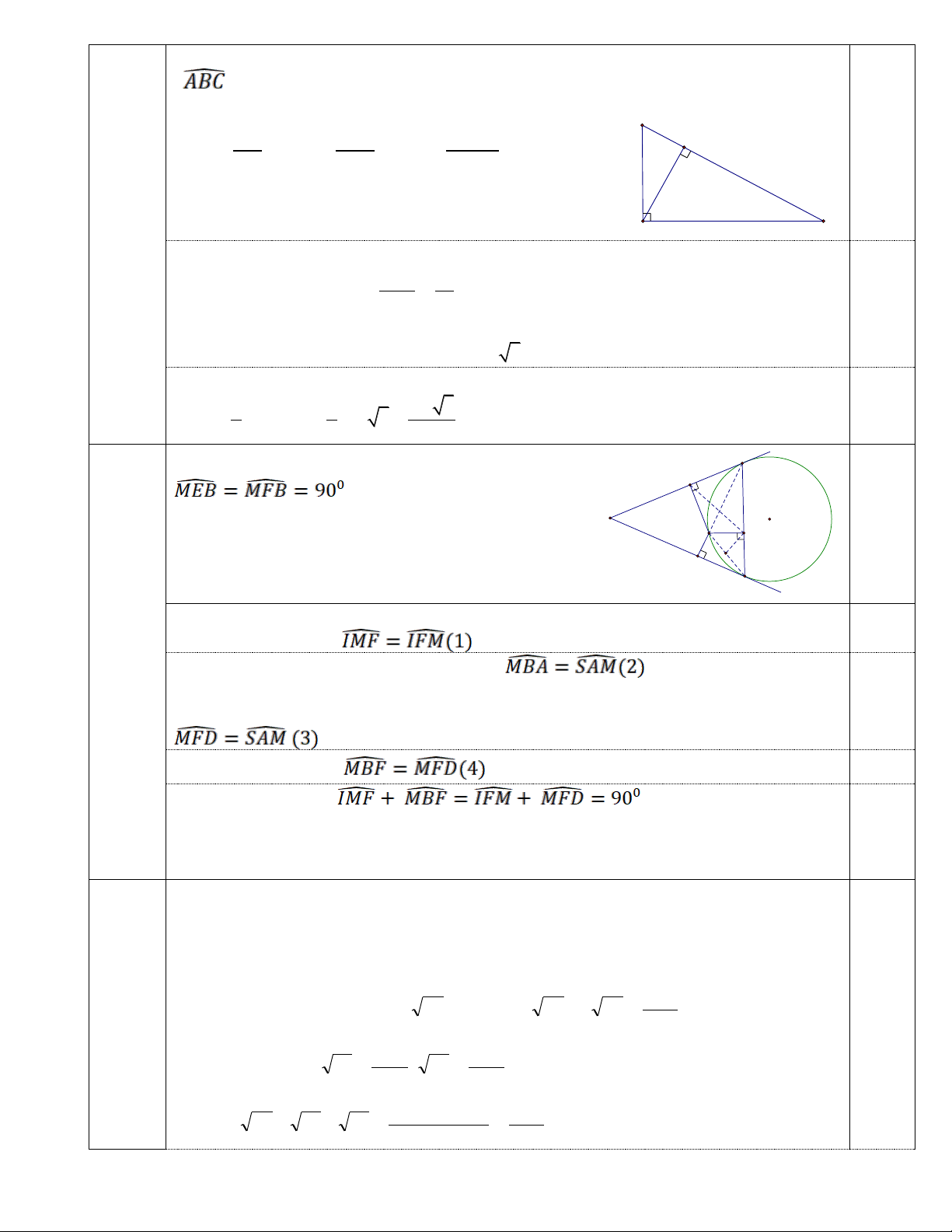
Câu 5. (2,0 điểm) Từ điểm S nằm ngoài đường tròn (O), kẻ hai tiếp tuyến SA, SB với
đường tròn (A, B là các tiếp điểm). M là điểm bất kì trên cung nhỏ AB (M  A, M  B).
Gọi D, E , F tương ứng là hình chiếu vuông góc của M trên các đường thẳng SA, SB, AB.
a) Chứng minh tứ giác MEBF là các tứ giác nội tiếp.
b) Chứng minh DF là tiếp tuyến của đường tròn đường kính MB.
Câu 6. (1,0 điểm) Cho a, b, c là các số thực dương thoã mãn : a + b + c = 3 .
Tìm giá trị nhỏ nhất của biểu thức : 2022 b a c b a c P    
ab bc ac 1 b 1 c 1 a
------------------------ HẾT -----------------------------
Giám thị không giải thích gì thêm
Họ và tên thí sinh ............................................................... Số báo danh ...........................
HƯỚNG DẪN CHẤM ĐỀ THI THỬ TOÁN 9
NĂM HỌC 2022 – 2023 (MĐ 02) Câu Nội dung Điểm
a) A A  2 45  2 20  5  6 5  4 5  5  3 5 1,0 b) với x  ; 0 x  1, ta có:    1 1  x 1 1 1 x 1   0,5 Câu 1 B B   :   :           (2,0 đ) x 1 x x x 1 x 1 x   x    1 x 1    x 1 x 1 x 1 x 1 x 1 x 1 1       0,5
x x  1 x x   : 1  x
x x   : 1 x x x    . 1 1 1 x 1 x
2x y  3 y  3 2xy  3 2xy  1  0,75 a)        x 3y  5
x 3(3 2x)  5 7  x 14 x  2
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (-1; 2) 0,25
b) Đường thẳng d và d song song với nhau khi và chỉ khi:  2 m  1  5  2 m  4 m  2       1,0 m  2 m 1  1 m  2 m  2
) Cho phương trình: x2 – 5x + m = 0 (m là tham số). Tìm m để phương trình Câu 2 trên có hai nghiệm x x x (3,0 đ) 1, x2 thỏa mãn: 1 1 2 c) Ta có: ∆ = 25 – 4.m 0,25 25
Để phương trình đã cho có nghiệm thì ∆  0  m  (*) 4
Theo hệ thức Vi-ét, ta có x1 + x2 = 5 (1); x1x2 = m (2). 0,25
Mặt khác theo bài ra thì x x  1 (3). Từ (1) và (3) suy ra x 1 2 1 = 2; x2 = 3 hoặc x1 = 3; 0,25 x2 = 2 (4)
Từ (2) và (4) suy ra: m = 6. Thử lại thì thoả mãn. 0,25
Gọi x, y số chi tiết máy của tổ 1, tổ 2 sản xuất trong tháng giêng (x, y  N* ), 0,25
ta có x + y = 1000 (1) (vì tháng giêng 2 tổ sản xuất được 1000 chi tiết). Do cải tiến kỹ
thuật nên tháng hai tổ 1 sản xuất được: x + 15%x, tổ 2 sản xuất được: y + 10%y. 0,25
Cả hai tổ sản xuất được: 1,15x + 1,10y = 1120 (2) Từ (1) Câu 4
, (2) ta có hệ phương trình: (1,0 đ) x y  1000  , 1 . 1 x  1 , 1 y  1100  , 05 . 0 x  20 x  400        0,25  15 , 1 x  1 . 1 y  1120  15 , 1 x  1 . 1 y  1120
x y 1000 y  600
<=> x = 400 và y = 500 (thoả mãn)
Vậy trong tháng giêng tổ 1 sản xuất được 400 chi tiết máy, tổ 2 sản xuất được 600 chi tiết máy. 0,25
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Biết AC = 6 cm và
= 300 . Tính độ dài đoạn thẳng BC và diện tích tam giác AHB.
Theo tỉ số lượng giác góc nhọn ta có C AC AC 6 H sin B   BC   BC   12 0,5 0 BC sin C sin 30 Vậy BC = 12 cm B A Câu 4
(1,0 đ) Áp dụng hệ thức cạnh và góc trong tam giác vuông ABC, ta có: 2 2 AC 6 2
AC BC.CH CH    3 + BC 12 0,25
BH BC CH BH  12  3  BH  9 cm + 2 2
AH BH.CH AH  9.3  AH  3 3 cm
Diện tích tam giác AHB là: 1 1 27. 3 S
 .AH.BH  .9.3 3  cm2 0,25 AHB 2 2 2 a) Tứ giác MEBF có: A D (gt)
Do đó tứ giác MEBF nội tiếp đường tròn đường S O 1,0 M F kính MB I E B
b) Gọi I là trung điểm của MB, Do tứ giác MEBF nội tiếp đường tròn đường kính 0,25 Câu 5 MC nên IF = IM =>
(2,0 đ) SA là tiếp tuyến của đường tròn (O) nên
(Góc nội tiếp và góc tạo
bởi tiếp tuyến và dây cung cùng chắn cung AM) 0,25
Chứng minh tương tự câu a ta có tứ giác MFAD là tứ giác nội tiếp. Do đó
( Hai góc nội tiếp cùng chắn cung DM) Từ (2) và (3) suy ra: 0,25 Từ (1) và (4) suy ra ( Tam giác MFC vuông tại F).
Do đó IF vuông góc với FD, Hay DF là tiếp tuyến của đường tròn đường kính 0,25 MB.
a b  3 c
Ta có: a b c  3  b c  3  a
a c  3 b Câu 6 3  c (1,0 đ)       
Vì a,b,c dương nên : a b 2 ab 3 c 2 ab ab 0,5 2   Tương tự ta có: 3 a 3 b bc  ; ac  2 2
9  (a b c) 9  3
Suy ra: ab bc ca    3 2 2 b a b a ab c b c b bc a c a c ac Ta có:   ;   ;   1 b 2 b 2 1 c 2 c 2 1 a 2 a 2 0,25 b a c b a c
ab bc ac 3 Suy ra:     1 b 1 c 1 a 2 2 Vậy : 2022 3 1345 P    3 2 2 0,25
Dấu (=) xẩy ra khi và chỉ khi : a = b = c = 1
Ghi chú: HS làm đúng các cách cho điểm tối đa.