
Preview text:
TRƯỜNG THCS NGHĨA TÂN
ĐỀ THI THỬ LẦN 1 – MÔN TOÁN LỚP 9 NHÓM TOÁN 9
NĂM HỌC: 2021 – 2022 Thời gian: 90 phút x x 1 2 x x x 2
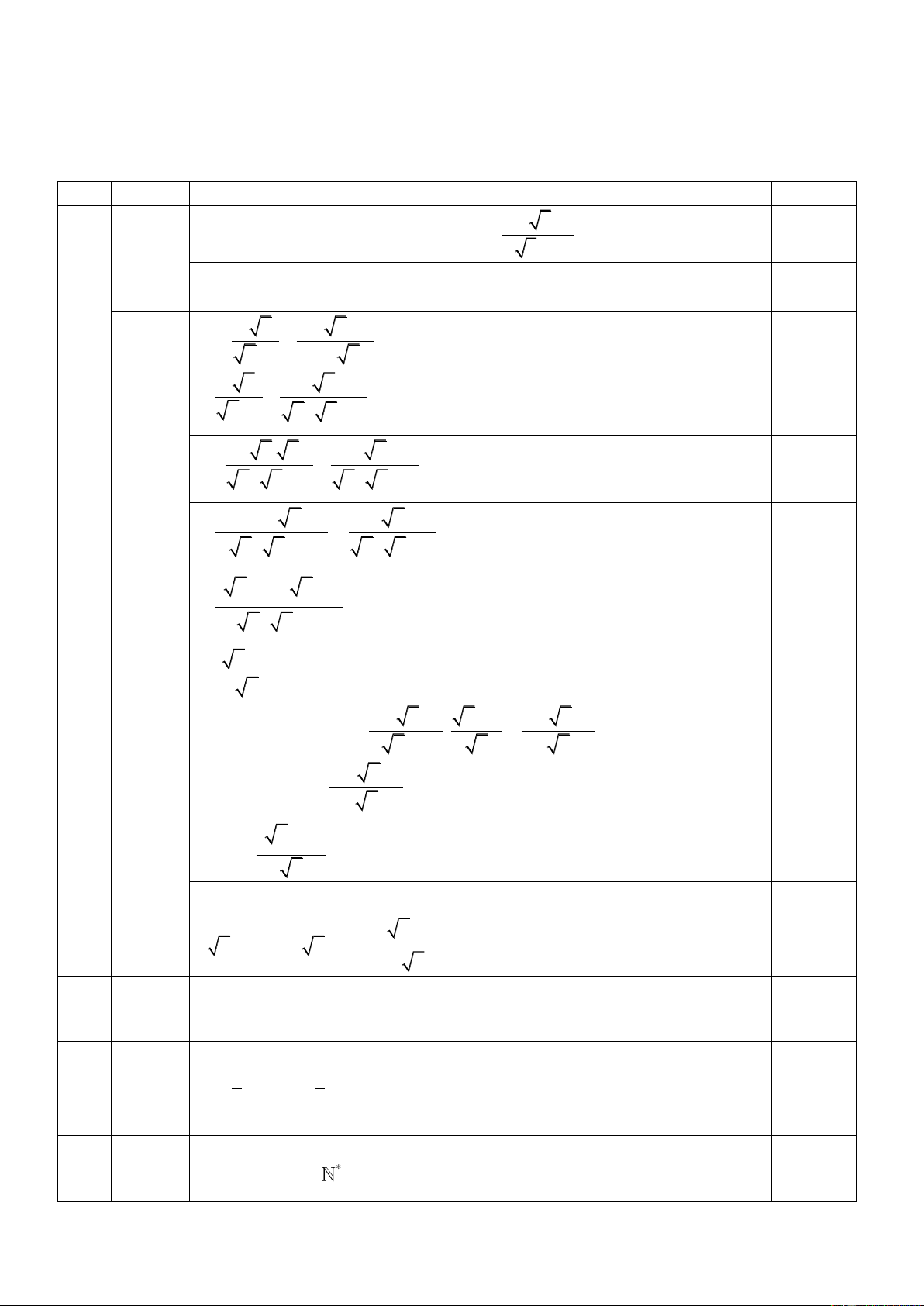
Bài I (2,0 điểm). Cho các biểu thức : A và B
với x 0; x 1. x 2 x 1 x x
1) Tính giá trị của biểu thức A khi x 9 . x 2 2) Chứng minh B . x
3) Cho P AB . So sánh P với 3. Bài II (2,0 điểm)
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch được 820 tấn thóc. Năm nay, đơn vị thứ
nhất làm vượt mức15% , đơn vị thứ hai làm vượt mức 20% so với năm ngoái. Do đó cả hai đơn vị
thu hoạch được 965 tấn thóc. Hỏi năm nay mỗi đơn vị thu hoạch được bao nhiêu tấn thóc?
2) Một dụng cụ làm bằng thủy tinh có dạng hình nón có chiều cao là 12 cm, đường kính đáy là 18 cm .
Tính thể tích dung dịch khi được đựng đầy trong dụng cụ đó ( lấy 3,14 ).
Bài III (2,0 điểm). 2
x 3 5 y 1 0
1) Giải hệ phương trình: 4 x
1 2 y 3 0 2) Cho phương trình 2
x 2m 2 x 2m 5 0 ( m là tham số)
a) Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của m .
b) Gọi x ; x là hai nghiệm của phương trình. Cho Q x 1 x
x 1 x 4 , tìm m để Q 4 . 1 2 2 1 1 2
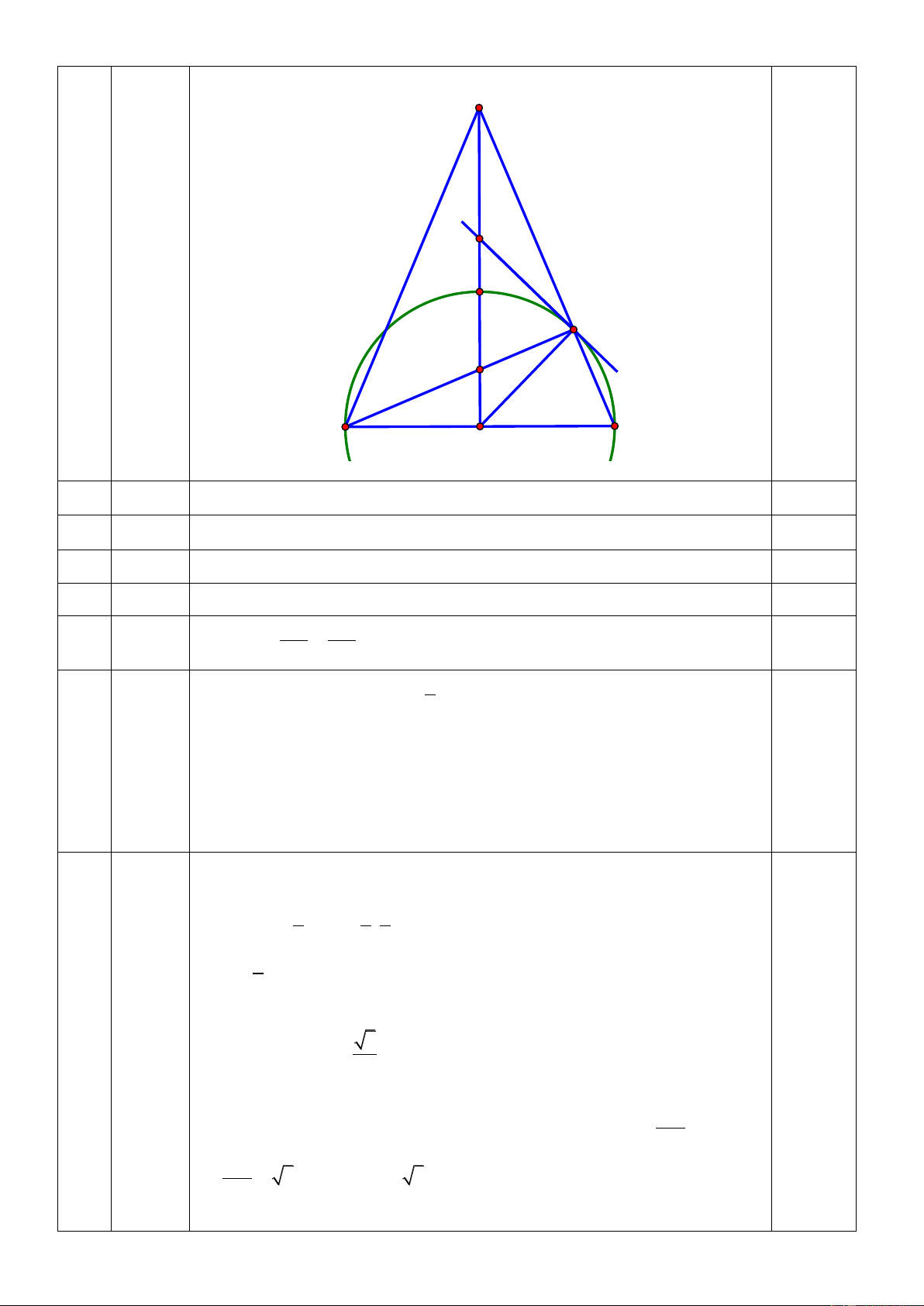
Bài IV(3,5 điểm). Cho nửa đường tròn tâm O , đường kính AB 2R . Lấy điểm C thuộc nửa đường tròn
CA CB. Qua O kẻ đường thẳng d vuông góc với AB , đường thẳng d cắt AC , nửa đường tròn và
BC lần lượt tại ; D E; F .
a) Chứng minh AOCF là tứ giác nội tiếp đường tròn. b) Chứng minh O . B AD O . D BF.
c) Tiếp tuyến của nửa đường tròn qua C cắt d tại I . Chứng minh I là trung điểm FD .
Tìm vị trí của điểm C trên nửa đường tròn để diện tích của tam giác ABC gấp 6 lần diện tích của tam giác DIC .
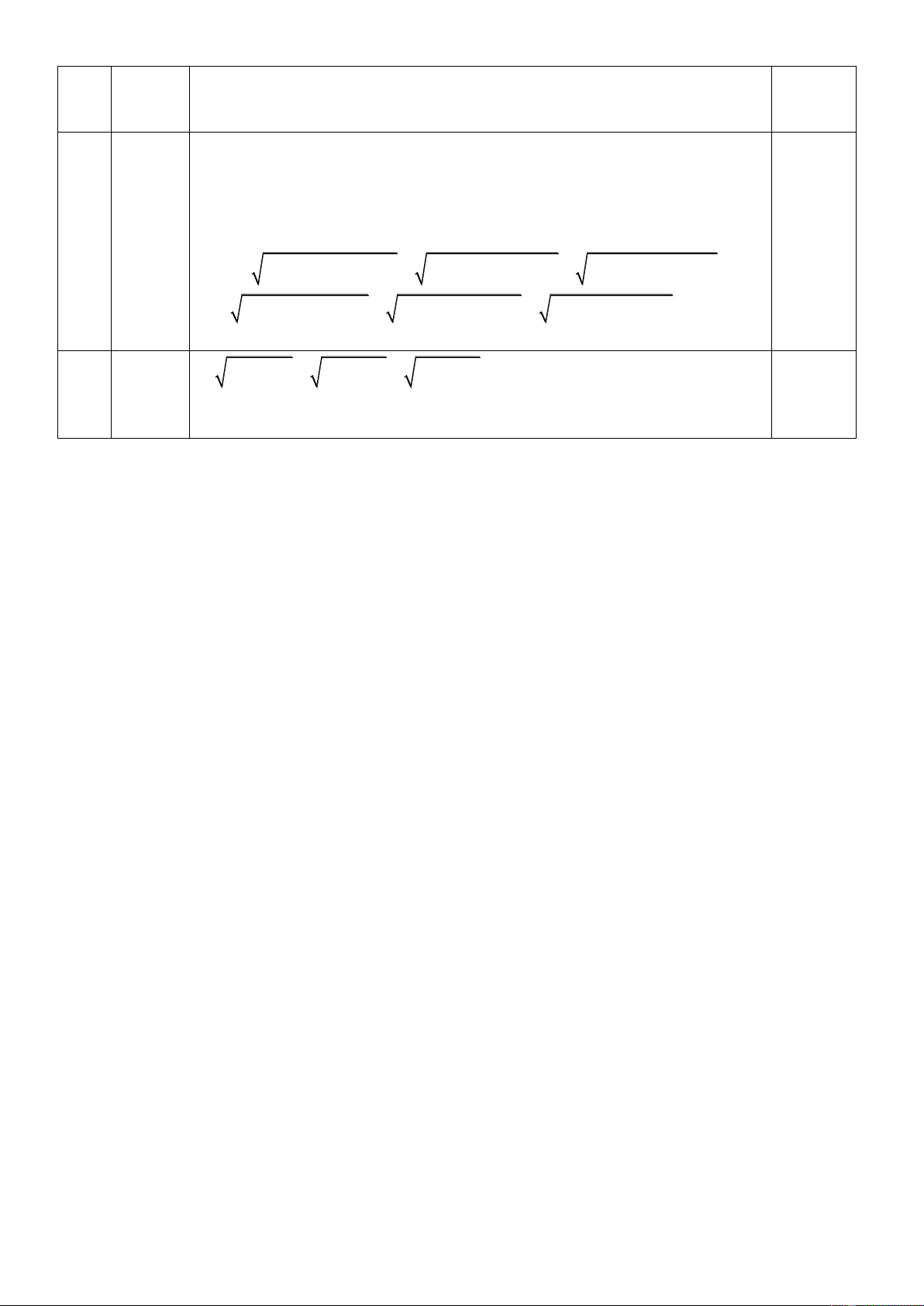
Bài V (0,5 điểm). Cho a 0;b 0;c 0 và a b c 1. Tìm giá trị lớn nhất của biểu thức : 2 2 2
M 5a 3a 1 5b 3b 1 5c 3c 1 . ---HẾT--- ĐÁP ÁN NĂM HỌC 2021- 2022 BÀI CÂU ĐÁP ÁN ĐIỂM I 1 0,5 đ
Thay x 9 (TMĐK) vào A ta có: 9 9 1 A 0,25 9 2 Tính đượ 13 c A 5 0,25 2 2 x x x 2 0,25 1,0đ B x 1 x x 2 x x x 2 x 1 x x 1 2 x. x x x 2 0, 25 x x 1 x x 1 2x x x 2 0, 25 x x 2 x x 1 x x 1
x 2 x 1 0,25 x x 1 x 2 x 3 x x 1 x 2 x x 1 0,5 đ Ta có: P AB P . x 2 x x x x 1 Xét hiệu P 3 3 0,25 x x 2 1 P 3 x
Với điều kiện x 0; x 1 suy ra được 0,25 x x 2 2 1 1 0; x 0 0 P 3 . x II 1
Bán kính đáy của nón là 18 : 2 9 cm 0,25 (0,5 đ)
Thể tích của dung dịch NaOH là: 0, 25 1 1 2 2
V . .R .h .3,14.9 .12 1017,36 3 cm . 3 3 2
Gọi số tấn thóc năm ngoái của đơn vị I và đơn vị II lần lượt là x , y (tấn thóc ) 0, 25 (1,5đ) (điều kiện * x, y
, x, y 820 )
Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch được 820 tấn 0, 25
thóc nên ta có phương trình: x y 820 1
Năm nay đơn vị thứ nhất thu hoạch vượt mức15% nên đơn vị thứ nhất 0, 25
làm được1,15x (tấn thóc ) , đơn vị thứ hai làm vượt mức 20% nên đơn vị
thứ hai làm được1, 2x (tấn thóc ) .
Năm nay, cả hai đơn vị thu hoạch được 965 tấn thóc nên ta có phương
trình 1,15x 1, 2 y 965 x y 820 0, 25 Từ
1 và 2 ta có hệ phương trình:
1,15x 1, 2 y 965 Giải hệ được 0, 25
x 380 (thỏa mãn). y 40 4
Vậy sản lượng năm nay đơn vị thứ nhất thu hoạch được là 0, 25 380 380.15% 437 tấn
Sản lượng năm nay đơn vị thứ hai thu hoạch được là 965 437 528 tấn III 1 2
x 3 5 y 1 0
2x 5y 11 0,5 (1,0 đ) Ta có 4 x
1 2 y 3 0
4x 2y 1 0 9 0,5 x 2 y 4 9
Vậy hệ phương trình có nghiệm ; 4 . 2 2 a 2
x 2m 2 x 2m 5 0 0, 25
(1,0 đ) Có m 2 ' 3 0 với mọi m Ta có m 2 3
0 với mọi m ' 0 với mọi m nên phương trình có hai 0, 25
nghiệm phân biệt với mọi m 2 b
Gọi x ; x là hai nghiệm của phương trình.Theo định lý Vi-et ta có : 0, 25 1 2
(1,0 đ) x x 2m4 1 2 x x 2m . 5 1 2
Ta có Q x 1 x
x 1 x 4 x x 2x x 4 1 2 2 1 1 2 1 2
Thay vào Q ta được: 2m 2 22m 5 4 0, 25 Tìm được m 1 IV 0, 25 F I E C D A B O 1 Chứng minh o
AOF ACF 90 0,25
O và C cùng nhìn đoạn AF dưới một góc o 90 0,25
AOCF là tứ giác nội tiếp đường tròn đường kính AF 2 Chứng minh A OD∽ F OB (g -g) 0,5 OD AD 0,5 O . B AD O . D BF. (đpcm) OB BF 3 1 0,25
Ta có CBA ICA ( cùng bằng sd AC ) 2 Mặt khác o
IFC CBA 90 ; o
FCI ICA 90 IFC FCI I
FC cân tại C IF IC Xét C
DF vuông tại C có o o
IFC IDC 90 ; FCI ICD 90 IDC ICD I
CD cân tại I
Do đó IF ID IC nên I là trung điểm FD . Đặt sin ABC 0,25 1 1 1 Ta có S S . . . CD CF . DIC 2 CDF 2 2 1 S . CA CB ABC 2
Tính các cạnh theo R và sin ABC . 3 Tìm được o sin ABC ABC 60 . 2 Cách khác: 2 BC S 6S S 3S . Mà A
BC ∽ FDC g g 3 ABC DIC A C B F C D DC BC o o
3 tan CDB 3 CDB 60 BDA 120 . DC D
AB cân tại D o o
DAB DBA 30 ABC 60 . V 0,25
Ta có: a 0; b 0; c 0; a b c 1 2 2 2 0 a, ,
b c 1 a a,b , b c . c Do đó : 2
M 4a 2 a 3a 2 1 4b 2 b 3b 2 1 4c 2 c 3c 1 2
4a a 3a 2
1 4b b 3b 2
1 4c c 3c 1 . 0,25
a 2 b 2 c 2 2 1 2 1 2 1
2a 2b 2c 3 5
Vậy MaxM 5 khi ( ; a ;
b c) là hoán vị (0; 0;1) .




