

Preview text:
PHÒNG GD&ĐT TÂN KỲ
KỲ THI THỬ TUYỂN SINH LỚP 10 THPT LẦN 1 NĂM HỌC 2024-2025 ĐỀ CHÍNH THỨC Môn thi : Toán
Thời gian làm bài: 120 phút, không kể thời gian giao đề
Câu 1. (2,5 điểm) a) Tính 64 16 4 . x x
b) Cho x 0; x 9 . Chứng minh rằng: 2 1 3 . 1 . x 3 x x 3
c) Tìm a, b để đường thẳng (d) y ax b đi qua điểm A(1;2) và song song với đường
thẳng y x 5 .
Câu 2. (2,0 điểm) a) Giải phương trình: 2
3x 7x 2 0 .
b) Cho phương trình bậc hai 2
x 5x 6 0 có hai nghiệm phân biệt x ; x . Không giải 1 2 phương trình 5 x 5 x
hãy tính giá trị của biểu thức 1 2 T . x x 2 1
Câu 3. (2,0 điểm)
a)Trong kỳ thi tuyển sinh vào lớp 10 của một trường THCS có 110 học sinh dự thi. Biết rằng 1
số học sinh trúng tuyển nhiều hơn 1 số học sinh không trúng tuyển là 23 học sinh. 4 5
Tính số học sinh trúng tuyển và số học sinh không trúng tuyển của trường đó ? x y
b) Giải hệ phương trình sau: 4 5
x 2y 1
Câu 4. (3,0 điểm)
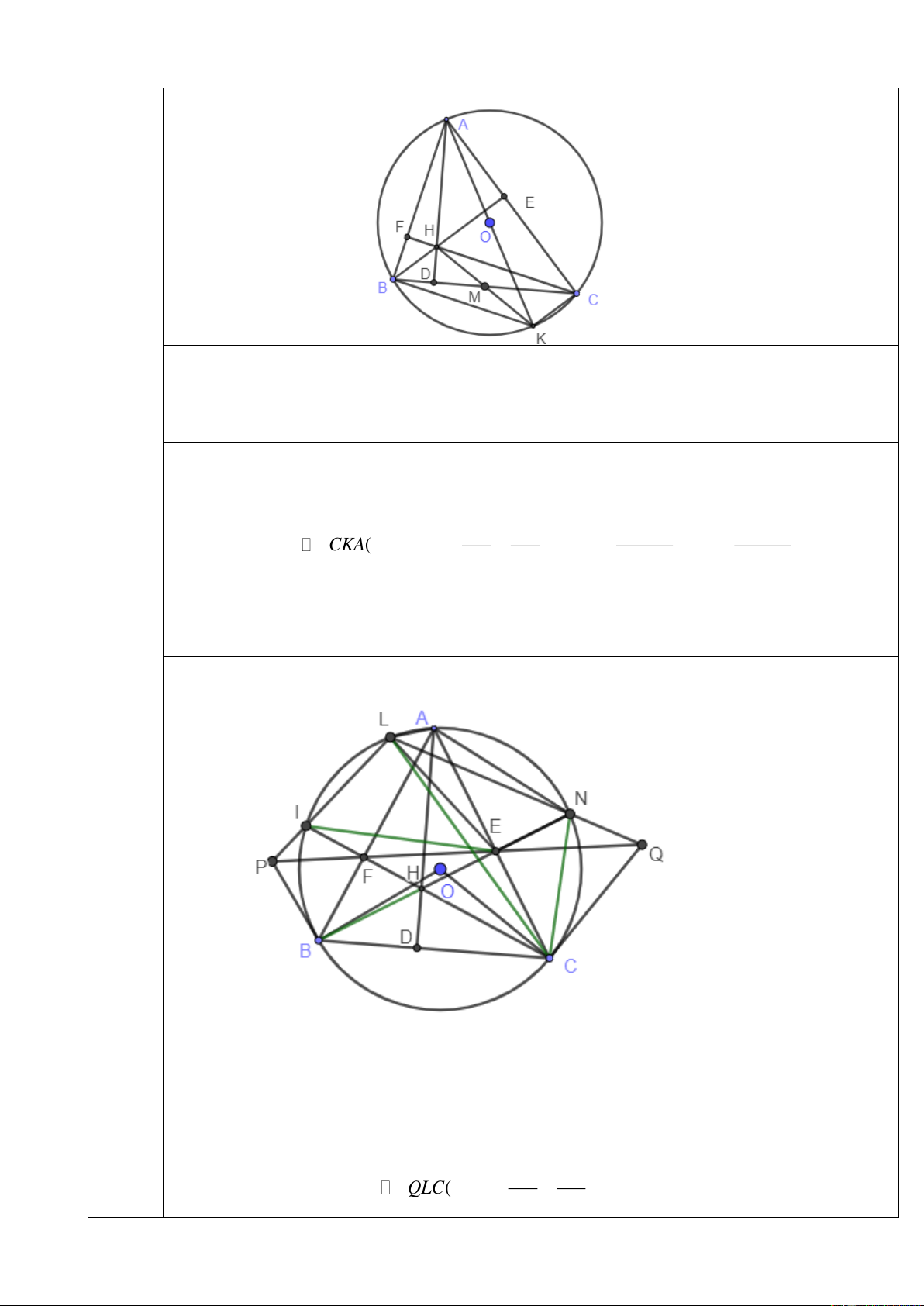
Cho tam giác ABC có 3 góc nhọn (AB AD, BE, CF cắt nhau tại H. Tia AO cắt (O) tại K . Gọi M là trung điểm của BC.
a) Chứng minh BDHF là tứ giác nội tiếp. AB AC b) Chứng minh . R
và M là trung điểm của KH. 2 AD
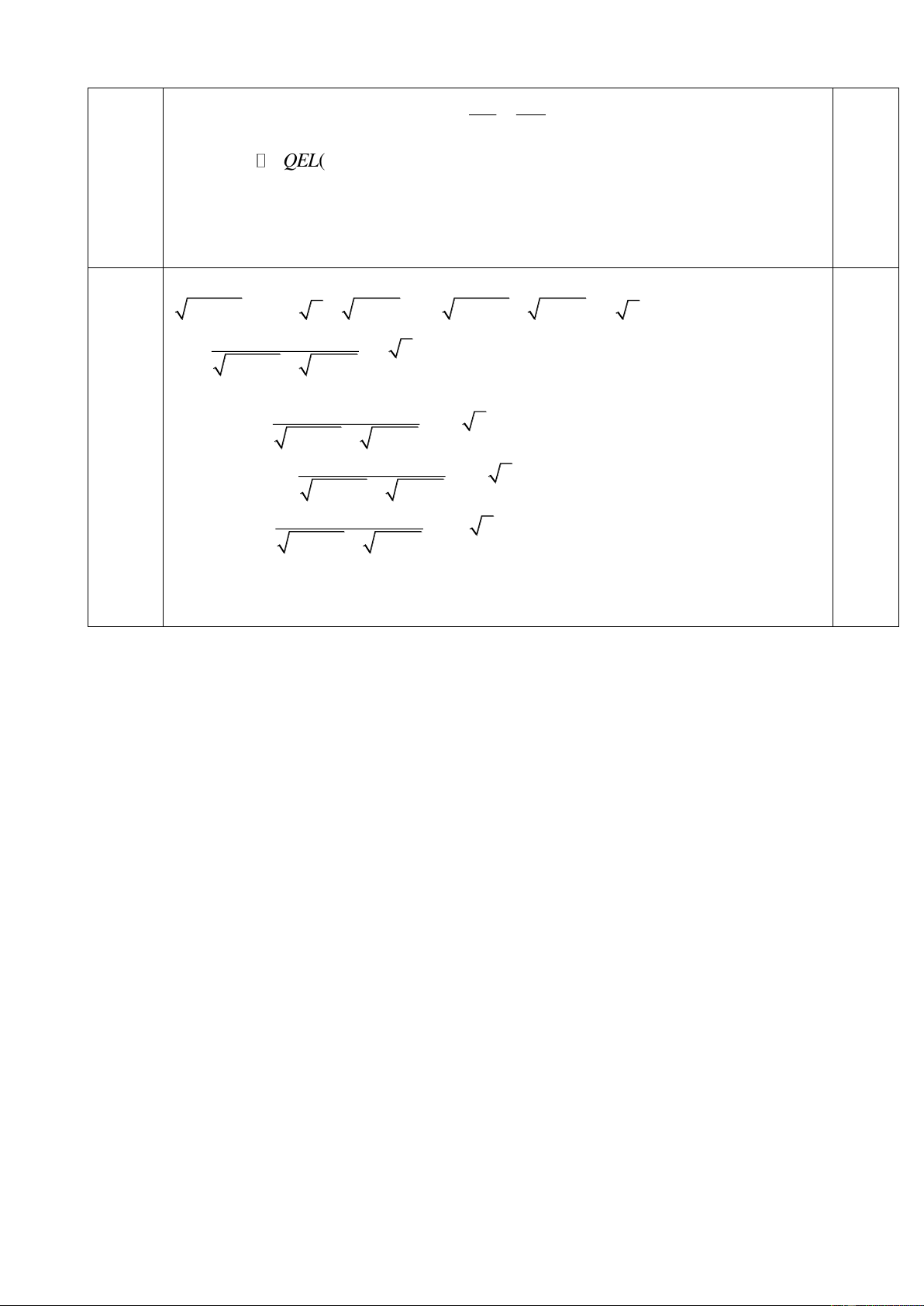
c) Đường thẳng EF cắt tiếp tuyến tại B, C của (O) lần lượt tại P, Q. BE, CF cắt (O) lần
lượt tại N, I. Giả sử QN cắt (O) tại L Chứng minh P, I, L thẳng hàng.
Câu 5. (0,5 điểm) Giải phương trình sau: 2 3 2
x 15 2 3 x x 8 .
……………………………….Hết…………………………………
ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ THI THỬ VÀO LỚP 10 NĂM HỌC 2024-2025 LẦN 1
(Môn Toán 9. Thời gian làm bài 120 phút) CÂU ĐÁP ÁN ĐIỂM
a) 64 16 4 8 4 2 6 0,5 0,25 0,25
b)Biến đổi vế trái ta có: 0,25 2 1 x 3 x
2 x ( x 3) x( x 3) ( x 3) x( x 3) . . 1 Câu1 x 3 x x 3 x ( x 3) x 3
( x 3) x ( x 3) 0,5 2,5 đ c) 0,25
Vì đường thẳng (d) song song với đường thẳng y x 5 nên a = 1 và b khác 5 0,25 0,25
Vì đường thẳng (d) đi qua A(1; 2) nên 2 1.1 b b 1(Thoả mãn) Vậy a = b =1 Câu 2 a) Ta có: 2 ( 7)
4.3.2 25 0 nên phương trình có 2 nghiệm phân biệt. 0,25 2,0 đ 0,25 ( 7 ) 25 ( 7 ) 25 1 x 2; x 0,25 1 2 2.3 2.3 3 0,25 b c 0,25
b) Theo hệ thức Viét ta có: x x
5; x .x 6 1 2 1 2 a a 2 2 0,25 5 x 5 x
(5 x )x (5 x )x
5(x x ) (x x ) 1 2 1 1 2 1 1 2 1 2 T x x x x 6 2 1 1 2 0,25 2 2
5(x x ) (x x ) 2x x 5.5 5 2.6 0,25 1 2 1 2 1 2 2 6 6
2)Gọi số học sinh trúng tuyển và không trúng tuyển lần lượt là a và b 0,25 * ( ;
a b N , a 110;b 110) (*)
Vì tổng số học sinh dự thi là 120 học sinh nên a + b = 110 (1) 0,25 1 0,25 Vì
số học sinh trúng tuyển nhiều hơn 1 số học sinh dự thi là 23 học sinh nên ta 4 5 Câu 3 0,25 2 điểm 1
có phưng trình 1 a – b = 23 (2) 0,25 (1,5 4 5 +0,5)
a b 110 0,25 a 100
Từ (1) và 2 ta có hệ phương trình: 1 1
( Thoả mãn điều kiện* ) a b 23 b 10 4 5
Vậy số học sinh trúng tuyển là 100 học sinh, số khọc sinh không trúng tuyển là 10 học sinh. 0,25 3 x 3
x 4y 5 x 1 b) 1 x
Vậy hpt có nghiêm (x, y) (1; 1 ) 0,25 x 2 y 1 y y 1 2 Vẽ hình đúng 0,5 điểm Câu 4 3 điểm a)Vì 0
HDB 90 (vì AD là đường cao cuả giác giác ABC 0,25 0,25 0
BFH 90 (vì CF là đường cao của tam giác ABC) 0,5 0 0 0
BFH HDB 90 90 180 => Tứ giác BDHF là tứ giác nội tiếp b)Ta có 0
KCA 90 ( góc nội tiếp chắn nữa đường tròn)
Xét DAB và C AK có: 0,25
DBA CKA (Cùng chắn cung AC), 0
ADB ACK 90 0,25 AD AC . AB AC . AB AC => D BA CK ( A gg) (gg) => AK R AB AK AD 2AD 0,25
CH / /BK ( cùng vuông góc AB).
BH / /CK ( cùng vuông góc AC).
=> BHCK là hình bình hành mà M là trung điểm của BC => M là trung điểm của HK 0,25 0,25 0,25 c) 0
BEC BFC 90 ( Tính chất đường cao) => tứ giác BCEF nội tiếp =>
FBC AEF mà QEC AEF (dối đỉnh) và ABC FBC ACQ QCA (cùng
chắn cung AC) => QEC QCE => Tam gác ECQ cân tại Q => QE = QC.(1)
Lại có tam giác QNC và tam giác QCL có QCN QLC (cùng chắn cung CN), QC QL
CQN LQC => 2 Q CN Q
LC(gg)
QC QN.QL (2) QN QC QE QN Từ (1) và (2). => 2
QE QN.QL
kết hợp EQN LQE => QL QE Q EN Q E (
L gg) QNE QEL LNE LEF mà LNE LNB LAB LAF
=> LAF LEF =>tứ giác ALFE nội tiếp => L thuộc (AEF)
Gọi L’ là giao điêm của PI với (O). Chứng minh tương tự trên ta suy ra L’thuộc
(AEF)=> L trùng L’, Vậy P, I, L thẳng hàng
Câu 5 ĐK: với mọi số thực x 0,5 2 3 2 2 2 3 điểm x 15 2 3 x x 8 x 15 x 8 3 x 2 0,25 7 3 3 x 2 2 2 x 15 x 8
Nhận thầy x 1 là nghiệm của phương trình đã cho. Với 7 x 1 thì 3 1;3 x 2 1 2 2 x 15 x 8 Với 7 0 x 1 thì 3 1;3 x 2 1 2 2 x 15 x 8 Với 7 x 0 thì 3 0;3 x 2 0 2 2 0,25 x 15 x 8
Vậy phương trình đã cho có nghiệm duy nhất x 1
(Học sinh làm cách khác đúng vẩn cho điểm tối đa)




