Đề thi thử Toán vào lớp 10 lần 2 năm 2023 phòng GD&ĐT Nghĩa Đàn – Nghệ An

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi thử môn Toán tuyển sinh vào lớp 10 THPT lần 2 năm 2023 phòng Giáo dục và Đào tạo huyện Nghĩa Đàn, tỉnh Nghệ An; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

54 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
PHÒNG GD&ĐT NGHĨA ĐÀN
(Đề thi gồm 01 trang)
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
LẦN 2, NĂM HỌC 2022 – 2023
Môn thi: Toán
Thời gian làm bài: 120 phút(không kể thời gian giao đề)
Bài 1.(2,5 điểm)
a) Tnh
2
1 5 5A
b) Rút gọn biu thc:
1
.
11
xx
Px
x x x







vi
0, 1xx
c) Xác định hàm số y = ax + b, biết đồ thị của hàm số đi qua hai đim A(- 4; 2) và cắt trục tung
tại đim có tung độ bằng 3 .
Bài 2.(1,5 điểm).
a) Gii hệ phương trnh:
2 3 5
21
xy
xy

b) Cho phương trnh
2
3 1 0xx
có hai nghiệm dương phân biệt x
1
, x
2
. Không gii
phương trnh tính giá trị biu thc:
12
11
A
xx

.
Bài 3:(2,0 điểm)
b) Hưng ng phong tro “V biển đo Trường Sa” một đội tu d định ch 280 tn hng ra
đo. Nhưng khi chun bị khi hnh th số hng hóa đã tăng thêm 6 tn so vi d định. V vy đội tu
phi b sung thêm 1 tu v mỗi tu ch t hơn d định 2 tn hng. Hi khi d định đội tu có bao nhiêu
chiếc tu, biết các tu ch số tn hng bằng nhau?
Bài 4.(3,0 điểm).
Cho (O; R) v đường thẳng d không có đim chung vi (O). Đim M thay đi trên d. Từ M kẻ
hai tiếp tuyến MA, MB đến (O,R) (A,B là hai tiếp đim). Đoạn thẳng OM lần lượt cắt đường thẳng AB
và (O, R) tại đim H, K.
a) Chng minh t giác MAOB nội tiếp;
b) AH. KM = AM.KH;
c) Xác định vị trí của đim M trên d sao cho bán knh đường tròn nội tiếp tam giác MAB có giá
trị nh nht.
Bài 5.(1,0 điểm). Gii hệ phương trnh
3 3 2 2
2
( 1) ( 1) 0
4 4 2 7
x y x y y x
x y x y
-------------------------Hết ---------------------
( Cán bộ coi thi không gii thích gì thêm)
Họ và tên thí sinh:...................................................................... Số báo danh:..........................
ĐỀ CHÍNH THỨC
ĐP N
Bài 1: .(2,5 điểm)
Nội dung
Điểm
a
(0.75đ)
2
1 5 5 1 5 5
5 1 5 1
A
0,5
0.25
b
(1.0đ)
1
.
11
21
.2
1
x x x x x
P
x
xx
xx
x
x
x


0.5
0.5
c
(0.75đ)
V đồ thị hàm số y = ax + b cắt trục tung tại đim có tung độ bằng 3 nên ta có
b = 3. Đồ thị hàm số y = ax + b đi qua hai đim A(-4; 2) nên ta có
4
1
2 . 4 3
2
4
1
3
4
x
aa
y
yx

0.25
0.25
0.25
Bài 2.(1,5 điểm).
Nội dung
Điểm
a
(0,75đ)
2 3 5 2 3 5
2 1 2 4 2
1
7 7 1
1
x y x y
x y x y
x
xx
y



0,5
0.25
b
(0,75đ)
Theo Viet
12
12
3
.1
xx
xx

Ta có A>0
2
2
1 2 1 2
12
12
2.
11
.
3 2.1
55
1
x x x x
A
xx
xx
A





0.25
0.25
0.25
Bài 3.(2,0 điểm):
Nội dung
Điểm
a
1.0đ
Diện tch đáy ngoi hnh trụ là:
2 2 2
3,14.1 3,14Rm

Th tích ngoài của hình trụ:
3
3.3,14 9,42m
Diện tch đáy trong hnh trụ là:
22
3,14.0,85 2,26865m
Th tích trong của hình trụ:
3
3.2,26865 6,8m
Th tích phần bê tông : 9,42 – 6,8 = 2,62
3
m
Th tích bê tng cần làm 10 chiếc ống cống như vy: 2,62.10 = 262
3
m
0.25
0.25
0.25
0.25
b
1,0 đ
Gọi số tàu của đội d định ch hng ra đo là x (chiếc)
ĐK: x nguyên dương
Mỗi tàu d định ch số tn hàng là

(tn)
Số tn hàng thc tế ch ra đo là 280 + 6 = 286 (tn)
Số tàu của đội thc tế ch hng ra đo là x + 1 (chiếc)
Mỗi tàu thc tế ch số tn hàng là


(tn)
Theo bi ra ta có phương trnh:



= 2
Gii phương trnh tm được: x
1
= 10 (Tha mãn )
x
2
= -14 ( không tha mãn)
Vy số tàu của đội d định ch hng ra đo là 10 (chiếc)
0,25
0,5
0,25
Bài 4.(3,0 điểm):
Nội dung
Điểm
0.5đ
0.5
a
1.0 đ
vì MA là tiếp tuyến của (O,R) nên 
= 
Vì MB là tiếp tuyến của (O,R) nên 
= 
xét t giác MAOB có 

= 
=> T giác MAOB nội tiếp đường tròn (T giác có tng hai góc đối bằng 180
0
).
0.5
0.5
b
0.75 đ
vì MA,MB là hai tiếp tuyến cắt nhau của (O,R) nên
AOK BOK AK BK
=> 

=> AK là tia phân giác của 
. => AK là tia phân giác của 
=> AK là đường phân giác của tam giác MAH =>




=> MK. AH = AM.KH
0.5
0.25
c
0.75đ
Vì MA,MB là hai tiếp tuyến cắt nhau của (O,R) nên MH là phân giác của 
Từ đó suy ra K l tâm đường tròn nội tiếp MAB.
Tam giác MAB cân tại M có MH l đường phân giác, đồng thời l đường cao nên
MH AB => KH AB
=> KH là bán kính của (K)
Vì K (O) mà KH nh nht OH ln nht (Vì KH + OH = R)
Kẻ OI d (I d) th I l đim cố định; P l giao đim của OI và AB
Ta có chng minh được OP.OI = OH.OM = R
2
=> OP = R
2
: OI.
Do OI không đi nên OP không đi.
Mà OH OP( đường vuông góc là ngắn nht).
Vy OH ln nht khi H P và M I.
Vy khi M l chân đường vuông góc kẻ từ O đến d thi bán knh đường tròn nội tiếp tam
giác MAB là nh nht.
0.25
0.25
0.25
Bài 5.(1,0 điểm):
Nội dung
Điểm
(1,0đ)
3 3 2 2
2
( 1) ( 1) 0 (1)
4 4 2 7 (2)
x y x y y x
x y x y
(ĐK:
4y
)
3 3 2 2 3 2 2 3
2 2 2 2
(1) ( 1) ( 1) 0 ( 1) ( 1) 0
( 1) ( 1 ) 0 ( )( 1) 0
x y x y y x x y x x y y
x x y y x y x y x y
22
0
0
1
10
xy
xy
xy
xy




Dễ thy x = y = 0 không là nghiệm của phương trnh (2)
Thay x = y + 1 vo phương trnh (2) được:
2
( 1) 4 4 2( 1) 7
2
2 1 4 4 2 2 7
22
4 4 8 4 4 4 4
2
2
42
4 2 4 4 2 0
4 2 4 4 6 0
4 1 4 2 0
4 2 0
4 3 4 2 0
y y y y
y y y y y
y y y y y y
yy
y y y y
y y y y
yy
y
yy
















42y
0y
(TMĐK)
Vi
01 yx
Vy nghiệm của hệ phương trnh l (x; y) = (1; 0)
0.5
0.5
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD&ĐT NGHĨA ĐÀN
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
LẦN 2, NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC Môn thi: Toán
(Đề thi gồm 01 trang)
Thời gian làm bài: 120 phút(không kể thời gian giao đề)
Bài 1.(2,5 điểm) a) Tính A    2 1 5  5  x x   1 
b) Rút gọn biểu thức: P    . x  
 với x  0, x  1 x 1 x 1    x
c) Xác định hàm số y = ax + b, biết đồ thị của hàm số đi qua hai điểm A(- 4; 2) và cắt trục tung
tại điểm có tung độ bằng 3 .
Bài 2.(1,5 điểm).
2x  3y  5
a) Giải hệ phương trình: 
x  2y  1  b) Cho phương trình 2
x  3x 1  0 có hai nghiệm dương phân biệt x1, x2. Không giải phương trình 1 1
tính giá trị biểu thức: A   . x x 1 2
Bài 3:(2,0 điểm)
a) Người ta đúc 10 ống cống thoát nước hình trụ bằng bê tông giống nhau
có đường kính ngoài 2m, chiều dài ống 3m và có bề dày 15cm. Hãy tính thể tích
bê tông cần mua để để làm 10 chiếc ống cống như thế.( Biết rằng π  3,14 ).
b) Hưởng ứng phong trào “Vì biển đảo Trường Sa” một đội tàu dự định chở 280 tấn hàng ra
đảo. Nhưng khi chuẩn bị khởi hành thì số hàng hóa đã tăng thêm 6 tấn so với dự định. Vì vậy đội tàu
phải bổ sung thêm 1 tàu và mỗi tàu chở ít hơn dự định 2 tấn hàng. Hỏi khi dự định đội tàu có bao nhiêu
chiếc tàu, biết các tàu chở số tấn hàng bằng nhau?
Bài 4.(3,0 điểm).
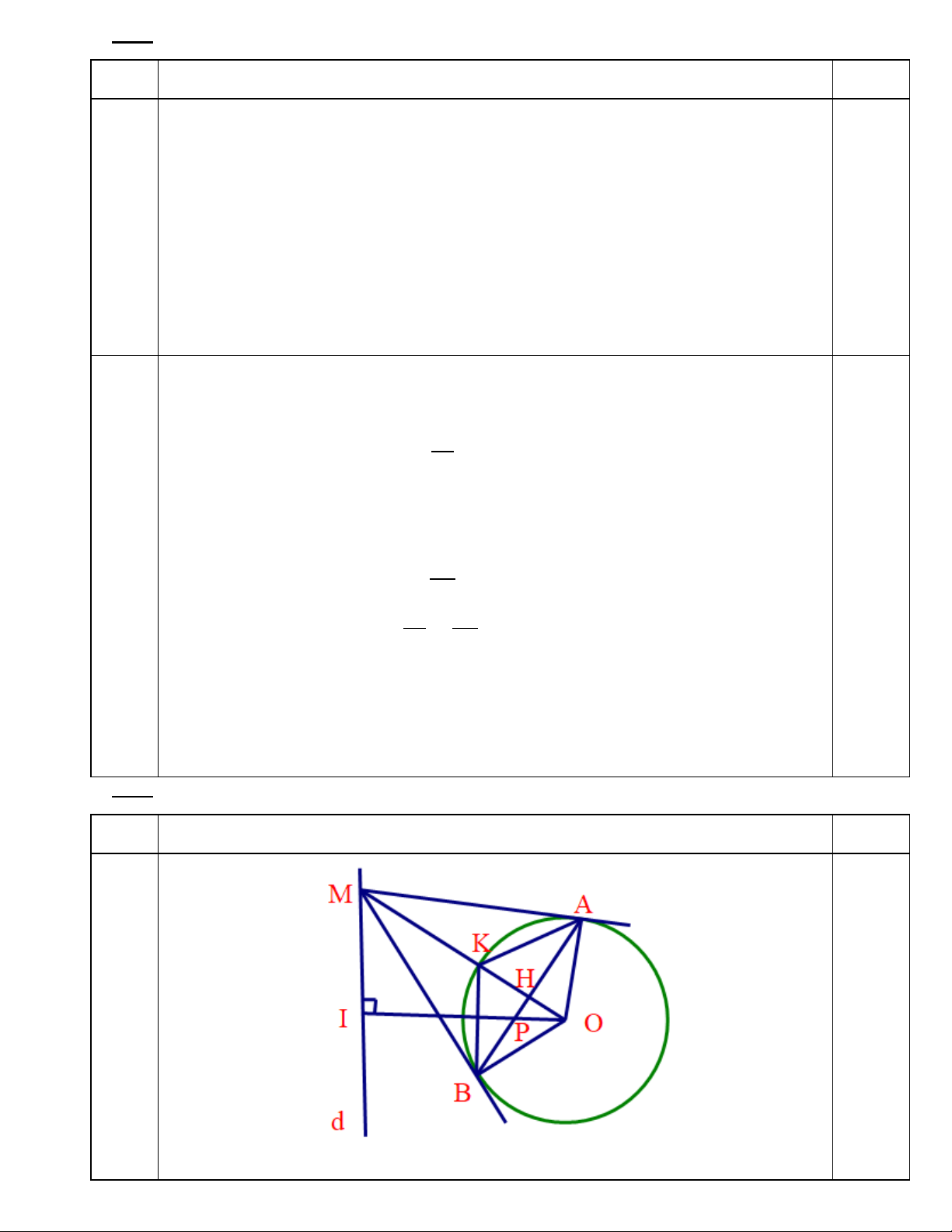
Cho (O; R) và đường thẳng d không có điểm chung với (O). Điểm M thay đổi trên d. Từ M kẻ
hai tiếp tuyến MA, MB đến (O,R) (A,B là hai tiếp điểm). Đoạn thẳng OM lần lượt cắt đường thẳng AB
và (O, R) tại điểm H, K.
a) Chứng minh tứ giác MAOB nội tiếp; b) AH. KM = AM.KH;
c) Xác định vị trí của điểm M trên d sao cho bán kính đường tròn nội tiếp tam giác MAB có giá trị nhỏ nhất. 3 3 2 2
x y  (x 1)y  (y 1)x  0
Bài 5.(1,0 điểm). Giải hệ phương trình  2
x  4 y  4  2x y  7 
-------------------------Hết ---------------------
( Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:...................................................................... Số báo danh:.......................... ĐÁP ÁN
Bài 1: .(2,5 điểm) Nội dung Điểm a 0,5 A    2 1 5  5  1 5  5 (0.75đ) 0.25  5 1 5  1 
x x x x x 1 0.5 P  . b
x  1 x  1 x (1.0đ) 2x x 1  0.5 .  2 x x 1 x
Vì đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ bằng 3 nên ta có 0.25
b = 3. Đồ thị hàm số y = ax + b đi qua hai điểm A(-4; 2) nên ta có c x  4     a   1 2 . 4  3  a  0.25
(0.75đ)y  2 4 1 0.25
y x  3 4
Bài 2.(1,5 điểm). Nội dung Điểm
2x  3y  5
2x  3y  5    a
x  2y  1 
2x  4y  2  0,5 (0,75đ) x 1  0.25
7x  7  x  1  y 1 x x  3 0.25 Theo Viet 1 2  x .x  1  1 2 Ta có A>0 b 2   0.25 (0,75đ) 1 1
x x  2 x .x 2 1 2 1 2 A       0.25 x x x .x  1 2  1 2 3  2.1   5  A  5 1
Bài 3.(2,0 điểm): Nội dung Điểm
Diện tích đáy ngoài hình trụ là: 2 2 2
R  3,14.1  3,14m 0.25 0.25
Thể tích ngoài của hình trụ: 3 3.3,14  9, 42m a
Diện tích đáy trong hình trụ là: 2 2
3,14.0,85  2, 26865m 1.0đ
Thể tích trong của hình trụ: 3 3.2, 26865  6,8m 0.25
Thể tích phần bê tông : 9,42 – 6,8 = 2,62 3 m 0.25
Thể tích bê tổng cần làm 10 chiếc ống cống như vậy: 2,62.10 = 262 3 m
Gọi số tàu của đội dự định chở hàng ra đảo là x (chiếc) 0,25 ĐK: x nguyên dương 280
Mỗi tàu dự định chở số tấn hàng là (tấn) 𝑥
Số tấn hàng thực tế chở ra đảo là 280 + 6 = 286 (tấn) b
Số tàu của đội thực tế chở hàng ra đảo là x + 1 (chiếc) 1,0 đ 286
Mỗi tàu thực tế chở số tấn hàng là (tấn) 𝑥+1
Theo bài ra ta có phương trình: 280 286 − = 2 0,5 𝑥 𝑥+1
Giải phương trình tìm được: x1 = 10 (Thỏa mãn )
x2 = -14 ( không thỏa mãn) 0,25
Vậy số tàu của đội dự định chở hàng ra đảo là 10 (chiếc)
Bài 4.(3,0 điểm): Nội dung Điểm 0.5đ 0.5
vì MA là tiếp tuyến của (O,R) nên MAO ̂ = 900 0.5
Vì MB là tiếp tuyến của (O,R) nên MBO ̂ = 900 a xét tứ giác MAOB có MAO ̂ + MBO ̂ = 1800 1.0 đ
=> Tứ giác MAOB nội tiếp đường tròn (Tứ giác có tổng hai góc đối bằng 1800). 0.5 0.5
vì MA,MB là hai tiếp tuyến cắt nhau của (O,R) nên AOK BOK AK BK => MAK ̂ = KAB
̂ => AK là tia phân giác của MAB
̂ . => AK là tia phân giác của MAH ̂ 𝐴𝑀 𝐾𝑀 b
=> AK là đường phân giác của tam giác MAH => = 𝐴𝐻 𝐾𝐻 0.75 đ => MK. AH = AM.KH 0.25
Vì MA,MB là hai tiếp tuyến cắt nhau của (O,R) nên MH là phân giác của AMB ̂
Từ đó suy ra K là tâm đường tròn nội tiếp ∆ MAB.
Tam giác MAB cân tại M có MH là đường phân giác, đồng thời là đường cao nên MH ⊥ AB => KH⊥ AB 0.25
=> KH là bán kính của (K)
Vì K ∈ (O) mà KH nhỏ nhất  OH lớn nhất (Vì KH + OH = R)
Kẻ OI ⊥ d (I ∈ d) thì I là điểm cố định; P là giao điểm của OI và AB c
Ta có chứng minh được OP.OI = OH.OM = R2 => OP = R2: OI.
0.75đ Do OI không đổi nên OP không đổi. 0.25
Mà OH ≤ OP( đường vuông góc là ngắn nhất).
Vậy OH lớn nhất khi H ≡ P và M ≡ I.
Vậy khi M là chân đường vuông góc kẻ từ O đến d thi bán kính đường tròn nội tiếp tam 0.25 giác MAB là nhỏ nhất.
Bài 5.(1,0 điểm): Nội dung Điểm 3 3 2 2
x y  (x 1)y  (y 1)x  0 (1) 0.5  (ĐK: y  4  ) 2
x  4 y  4  2x y  7 (2)  3 3 2 2 3 2 2 3
(1)  x y  (x 1) y  ( y 1)x  0  x  ( y 1)x  (x 1) y y  0 2 2 2 2
x (x y 1)  y (x 1 y)  0  (x y )(x y 1)  0 2 2 x y  0 x y  0    
x y 1  0 x y 1
Dễ thấy x = y = 0 không là nghiệm của phương trình (2)
Thay x = y + 1 vào phương trình (2) được: 0.5 2 ( y  1)  4
y4  2( y  1)  y  7 (1,0đ) 2  y 2 y 1  4
y4 2 y2 y7 2 2  yy4 y4 8
  y y44 y4 4 2 2  y   y4 2       yy4 2  y4 y4 2 0       y y4 2  y4 y4 6  0     y4 1  y4 2     0        y4  2  0     y 4 2  y4 3  y4 2     0      y  0 (TMĐK)
Với y  0  x  1
Vậy nghiệm của hệ phương trình là (x; y) = (1; 0)