Đề thi thử Toán vào lớp 10 lần 2 năm 2024 – 2025 phòng GD&ĐT Tân Kỳ – Nghệ An
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi thử môn Toán tuyển sinh vào lớp 10 THPT lần 2 năm học 2024 – 2025 phòng Giáo dục và Đào tạo huyện Tân Kỳ, tỉnh Nghệ An; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2024-2025
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
PHÒNG GD&ĐT TÂN KỲ
KỲ THI THỬ TUYỂN SINH LỚP 10 THPT LẦN 2 NĂM HỌC 2024-2025 ĐỀ CHÍNH THỨC Môn thi : Toán
Thời gian làm bài: 120 phút, không kể thời gian giao đề
Câu 1. (2,5 điểm) a) Tính 27 − 48 + 12 . b) Cho x +
x > 0 . Rút gọn biểu thức P = 1 1 2 − . . x x + 2 2
c) Tìm a, b để đường thẳng (d) y = ax +b đi qua điểm A(-1; 2 ) và cắt trục tung tại
điểm có tung độ bằng 3.
Câu 2. (2,0 điểm) a) Giải phương trình: 2
2x + 5x −1 = 0 .
b) Cho phương trình bậc hai 2
x + 6x − 2 = 0 có hai nghiệm phân biệt x ; x . Không giải 1 2
phương trình hãy tính giá trị của biểu thức 1 1 2 T = +
+ x − 6x + 2024 . 1 2 x x 2 1
Câu 3. (2,0 điểm)
a) Để tri ân khách hàng, một siêu thì điện máy đã giảm giá nhiều mặt hàng đề kích cầu mua
sắm. Giá niêm yết một chiếc tủ lạnh Samsung và một chiếc máy giặt Toshiba có tổng số tiền
là 25,4 triệu đồng nhưng trong dịp này giá chiếc tủ lạnh giảm 40% giá niêm yết và giá chiếc
máy giặt giảm 25% giá niên yết nên cô Liên đã mua hai mặt hàng trên với tổng số tiền là
16,77 triệu đồng. Hãy tính giá tiền niêm yết của mỗi mặt hàng trên?
b) Bác An muốn đúc một cống nước hình trụ, không có đáy, cao 1,1m; thành cống dày
8cm và đường kính vành ngoài của cống là 1,2m. Thể tích bê tông cần dùng để đúc cống là bao nhiêu 3
m ? (Bỏ qua hao phí, làm tròn kết quả đến hai chữ số ở phần thập phân và lấy π = 3,14).
Câu 4. (3,0 điểm)
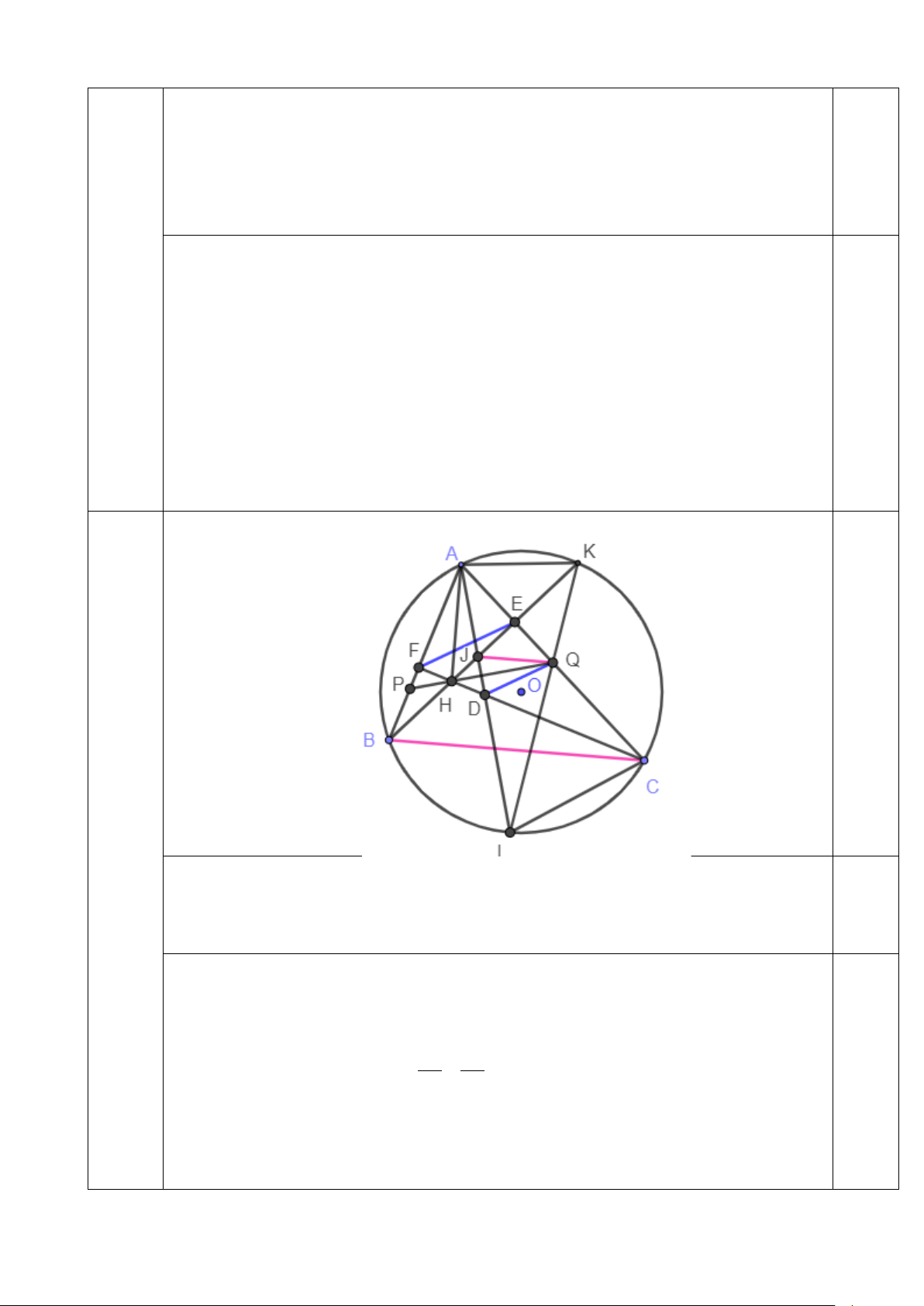
Cho tam giác ABC có 3 góc nhọn (AB BE, CF cắt nhau tại H tia BE cắt (O) tại K (K khác B).
a) Chứng minh tứ giác BCEF là tứ giác nội tiếp.
b) Tia phân giác của góc BAC cắt BE và (O) lần lượt tại J, I ( I khác A). IK cắt AC tại
Q. QH cắt AB tại P. Chứng minh IJ.IA = .
IQ IK và tam giác APQ cân. c. Chứng minh 1 1 1 + = . BC EF QJ 2 2
x + y − 2xy + 5x −3y + 4 = 2 (x + )1( y − )1
Câu 5 (0,5 điểm). Giải hệ phương trình: 2
5x − 6 + 16 − 3y = 2x − 2x + y − 4
……………………………….Hết…………………………………
ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ THI THỬ VÀO LỚP 10 NĂM HỌC 2024-2025 LẦN 2
(Môn Toán 9. Thời gian làm bài 120 phút) CÂU ĐÁP ÁN ĐIỂM
a) 27 − 48 + 12 = 3 3 − 4 3 + 2 3 = 3 0,5 0,25 0,25
b)Biến đổi vế trái ta có: 1 1 x + 2 x + 2 − x x + 2 2( x + 2) 1 0,25 − . = . = = Câu1 x x + 2 2 x( x + 2) 2 x( x + 2),2 x 0,5 2,5 đ c)
Vì d cắt trục tung tại điểm có tung độ bằng 3 nên b = 3 0,25
Vì đường thẳng (d) đi qua A(-1; 2) nên 2 = a( 1)
− + b = −a + 3 => a =1 0,25 Vậy a =1, b =3 0,25 a) Ta có: 2 ∆ = 5 − 4.2.( 1
− ) = 33 > 0 nên phương trình có 2 nghiệm phân biệt. 0,25 Câu 2 5 − + 33 5 − − 33 0,25 2,0 đ x = ; x = 0,25 1 2 4 4 0,25
b)Theo định lí Vi-ét ta có: 0,25 x + x = 6 − 1 2 . x .x = 2 − 1 2 0,25 1 1 + 2 x x 1 2 T = +
+ x − 6x + 2024 = + ( 6
− x + 2) − 6x + 2024 1 2 1 2 x x x x 0,25 2 1 1 2 0,25 6 T − =
− 6(x + x ) + 2026 = 3 − 6( 6) − + 2026 = 2065 1 2 2 −
Gọi giá tiền niêm yết của chiếc tủ lạnh Samsung là x (triệu đồng) và giá tiền
niêm yết của chiếc máy giặt Toshiba là y (triệu đồng). ĐK: x,y > 0 0,25
Vì tổng giá tiền niêm yết của chiếc tủ lạnh Samsung và chiếc máy giặt
Toshiba là 25,4 triệu đồng nên ta có phương trình: x + y = 25,4 0,25
Câu 3 Số tiền phải trả cho chiếc tủ lạnh khi được giảm 40% giá niêm yết là:
2 điểm 60%x (triệu đồng) (1,5 0,25 +0,5)
Số tiền phải trả cho chiếc máy giặt khi được giảm 25% giá niêm yết là: 75%y (triệu đồng)
Vì cô Liên đã mua hai mặt hàng trên với tổng số tiền là 16,77 triệu đồng nên
ta có phương trình: 60%x + 75%y = 16,77 0,25 a) x + y = 25,4
60%x + 75%y =16,77 x =15,2
Giải hệ phương trình này ta được: (tm) 0,25 y =10,2
Vậy giá tiền niêm yết của chiếc tủ lạnh Samsung là 15,2 (triệu đồng) và giá 0,25
tiền niêm yết của chiếc máy giặt Toshiba là 10,2 (triệu đồng) Đổi 8 cm = 0,08 m
Bán kính vành ngoài của cống là: R= 1,2 : 2= 0,6 (m) 0,25 b)
Bán kính vành trong của cống là r = R – 0,08 = 0,6 - 0,08= 0,52m
Thể tích bê tông cần dùng là: 2 2 2 2
V = πR h −πr h = 3,14.1,1.(0,6 − 0,52 ) 0,25 3 ≈ 0,31(m )
Vậy thể tích bê tông cần dùng là 0,31 3 (m ) Vẽ hình đúng 0,5 điểm Câu 4 3 điểm a)Vì 0
BEC = 90 (vì BE là đường cao cuả giác giác ABC 0,25 0 0,25
BFC = 90 (vì CF là đường cao của tam giác ABC) 0,5 => = 0
BFC BEC = 90 => Tứ giác BCÈ là tứ giác nội tiếp
b)Vi AI là phân giác của góc BAC nên = => = BAI CAI BI CI => sđ 0,25 + (BI AK):2=sđ +
(CI AK):2=> = AJK AQK => = KJI AQI
Xét tam giác IQA và tan giác ỊK có góc AIQ chung và = KJI AQI 0,25 =>∆ ∆ ( ) IQ IJ IQA IJK gg => = => IJ.IA = . IQ IK (Đpcm) IA IK Vì =
AJK AQK => Tứ gác AKQJ nội tiếp 0,25 => = = =
AQJ AKJ AKB ACB => QJ / /BC mà BC ⊥ AH => QJ ⊥ AH mà HE ⊥ QA 0,25
=> J là trực tâm của tam giác AHQ =>AJ vuông góc PQ mà AJ là
phân giác của góc PAQ => Tam giác APQ cân tại A
c) Vì QJ// BC nên QJ EQ = (1) BC EC
Gọi D là giao điểm của AI và CF. ta có 0,25 = = = = =
DCQ BCE EBF ABK AIK DIQ => Tứ giác DICQ nội tiếp
=> = = = => / / QD CQ AQ AIC ABC AEF DQ FE => = (2) EF CE
Từ (1) và (2) => QJ QD + =1 (3) BC EF
Lại có = = =
QJD AKI ACI JDQ => Tam giác QJD cân tại Q => QJ = QD (4) 0,25
Từ (3) và (4) => QJ QJ 1 1 1 + =1 => + = BC EF BC EF QJ
Câu 5 Giải hệ phương trình: 0,5 2 2 điểm
x + y − 2xy + 5x − 3y + 4 = 2 ( x + ) 1 ( y − ) 1 (1) 2
5x − 6 + 16 − 3y = 2x − 2x + y − 4 (2) ĐKXĐ: 6 16
x ≥ ; 1≤ y ≤ . 5 3 0,25 2 2
pt (1) : x + y − 2xy + 5x − 3y + 4 = 2 (x + ) 1 ( y − ) 1
⇔ x +1− 2 (x + ) 1 ( y − ) 2 2
1 + y −1+ x + y + 4 − 2xy + 4x − 4y = 0
⇔ ( x +1 − y −1)2 + (x − y + 2)2 = 0 Với
x +1 − y −1 = 0 ⇔ ⇔ y = x + 2
x − y + 2 = 0
y=x+2 thay vào pt (2) ta được: 2
5x − 6 + 10 − 3x = 2x − x − 2
⇔ ( 5x − 6 − 2) + ( 10 − 3x − 2) 2 = 2x − x − 6 5(x − 2) 3(x− 2) ⇔ − = (x − 2)(2x+ 3) 0,25 5x − 6 + 2 10 − 3x + 2 5 3 (x 2) 2x 3) ⇔ − − − − = 0
5x 6 2 10 3x 2 − + − +
* TH1: x – 2 = 0 <=> x = 2 (TM) => y = 4 (TM) * TH2: 5 3 2x 3) − − − = 0 (3) 5x 6 2 10 3x 2 − + − + ĐK của pt (3) là: 6 10 ≤ x ≤ 5 3 - Với 6 10 ≤ x ≤ 5 5
⇒ 5x − 6 + 2 ≥ 2 ⇒ ≤ 5 3 5x − 6 + 2 2 5 5 1 3 3 − ⇒ − ≤ − = < 0 (*) 5x − 6 + 2 2 2 - Với 6 10 3 ≤ x ≤ ⇒ − < 0 5 3 10 − 3x + 2 - Với 6 10 12 20 20 12 ≤ x ≤ ⇒ ≤ 2x ≤ ⇒ − ≤ 2 − x ≤ − ⇒ 2 − x < 0 5 3 5 3 3 5 3 − ⇒ − 2x < 0 (**) 10 − 30 + 2
Từ (*) và (**) => pt (3) vô nghiệm
Vậy hệ phương trình có nghiệm duy nhất là: x = 2; y = 4
(Học sinh làm cách khác đúng vẩn cho điểm tối đa)