Đề thi thử Toán vào lớp 10 lần 2 năm 2024 – 2025 phòng GD&ĐT Thái Hòa – Nghệ An

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ VÀO LỚP 10 THPT NĂM HỌC 2024-2025 (Lần 2) THỊ XÃ THÁI HÒA Môn: Toán học
Thời gian làm bài: 120 phút
Câu 1 (2,5 điểm)
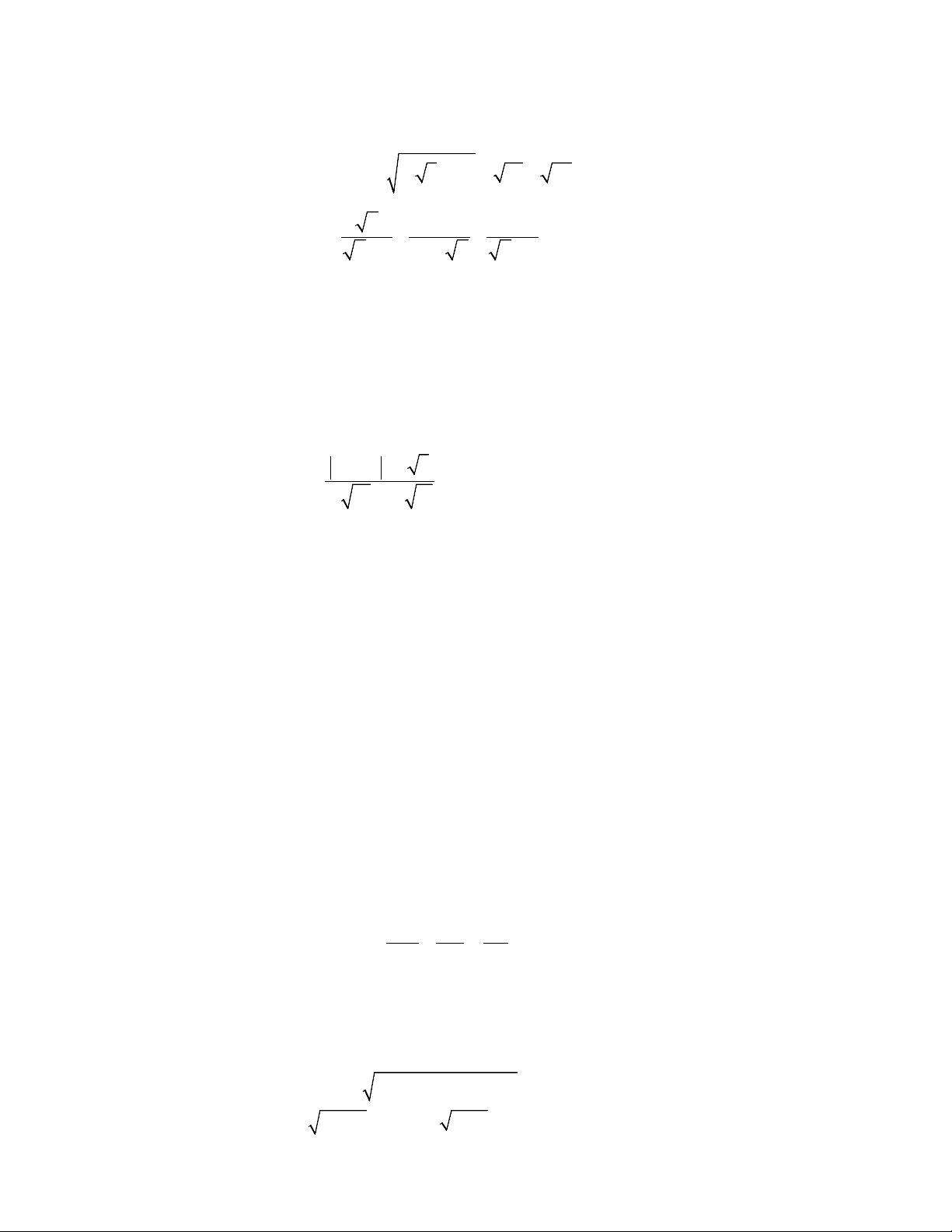
1) Tính giá trị của biểu thức A = ( + )2 3 3 1 + 12 − 75.   2) Rút gọn biểu thức x 25 1 B =  − . 
với x > 0 và x ≠ 25.
x 5 x 5 x  − − x +   5
3) Xác định các hệ số a, b của hàm số y = ax + b, biết rằng đồ thị của hàm số song song với
đường thẳng y = 3x − 2 và cắt trục tung tại điểm có tung độ bằng 3. −
Câu 2 (2,0 điểm) 1) Giải phương trình 2
x − 3x −10 = 0. 2) Cho phương trình 2
x − 4x +1 = 0 có hai nghiệm dương x , x . Không giải phương trình, hãy 1 2 − −
tính giá trị của biểu thức x x 8 3 1 2 P = . x x + x x 1 2 2 1
Câu 3 (2,0 điểm)
1) Hai đội công nhân cùng làm chung một công việc thì sau 15 ngày làm xong. Nếu đội thứ
nhất làm riêng trong 6 ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó trong 10 ngày thì cả
hai đội hoàn thành được 50% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao nhiêu ngày mới xong công việc trên ?
2) Một thùng nước có dạng hình trụ với chiều cao 1,8m và đường kính đáy 1,2m. Người ta
sơn toàn bộ phía ngoài mặt xung quanh của thùng nước này (trừ hai mặt đáy). Tính diện tích bề
mặt được sơn của thùng nước đó (lấy π ≈ 3,14 ).
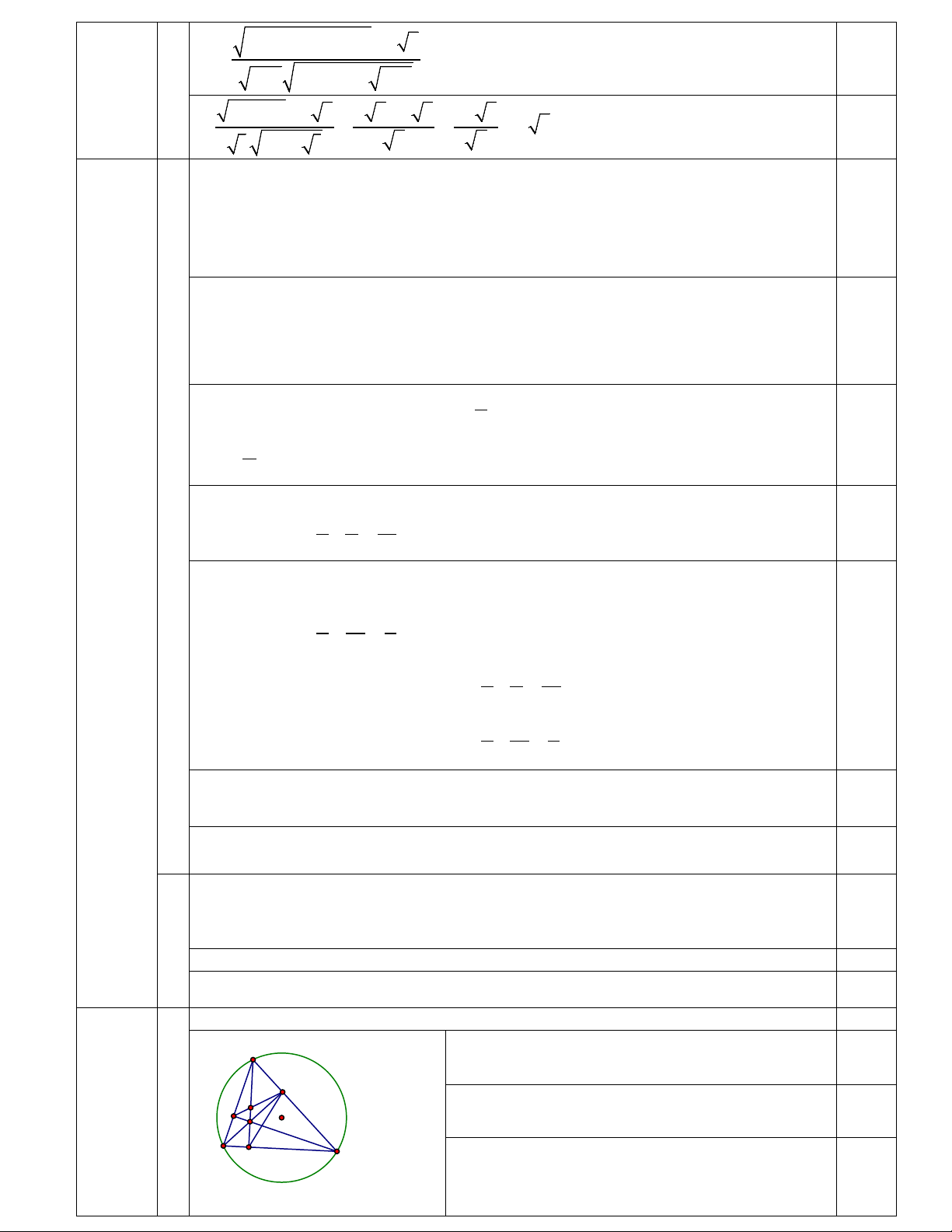
Câu 4 (3,0 điểm) Cho đường tròn (O) và dây BC cố định không đi qua tâm .
O Điểm A di động
trên cung lớn BC sao cho tam giác ABC nhọn. Các đường cao AD, BE và CF của tam giác
ABC cắt nhau tại điểm H. Gọi I là giao điểm của AD và EF.
1) Chứng minh CEHD là tứ giác nội tiếp. 2) Chứng minh  =  DEH FEH và 1 1 2 + = . DH DA DI
3) Tia AD cắt đường tròn (O) tại điểm M và tia ME cắt đường tròn (O) tại điểm N ( M
khác A và N khác M ). Gọi K là giao điểm của BN và EF. Chứng minh đường thẳng AK luôn
đi qua một điểm cố định khi A thay đổi.
Câu 5 (0,5 điểm)
x + 2 = (3y − 2x − )1( y +  )1
Giải hệ phương trình  .
 3y − 2 + y + 2 = x + 3 + 2xy --- HẾT ---
Họ và tên thí sinh: ................................................. SBD:............................
HƯỚNG DẪN CHẤM THI THỬ LỚP 10 LẦN 2 NĂM HỌC 2024 - 2025 MÔN THI: TOÁN
(Hướng dẫn chấm này có 04 trang) Câu ý Nội dung Điểm
Tính giá trị của biểu thức A = ( + )2 3 3 1 + 12 − 75. 1,0
1) A=3 3+1+2 3−5 3 (lưu ý: HS tính được từng căn cho 0,25 điểm) 0,75 =1. 0,25  
Rút gọn biểu thức x 25 1 B =  − . 
với x > 0 và x ≠ 25. 1,0
x 5 x 5 x  − − x +   5  x 25  1 B =  −   0,25 x 
( x −5) x( x −5) . x +5 2)  x − 25 1 Câu 1 =
x ( x −5). x +5 0,25 (2,5 điểm)
( x −5)( x +5) 1 = 0,25
x ( x −5) . x +5 1 = . 0,25 x
Xác định các hệ số a, b của hàm số y = ax + ,
b biết rằng đồ thị của hàm số song
song với đường thẳng y = 3x − 2 và cắt trục tung tại điểm có tung độ bằng 3. − 0,5 a = 3
3) Vì đồ thị của hàm số song song với đường thẳng y = 3x − 2 nên  . 0,25 b  ≠ 2 −
Vì đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 3 − nên b = 3 − (thoả
mãn). Vậy a = 3 và b = 3. − 0,25
Giải phương trình 2
x − 3x −10 = 0. 1,0 Phương trình 2
x − 3x −10 = 0 có a =1, b = 3, − c = 10 − 0,25 nên ∆ = (− )2 3 − 4.1.( 10
− ) = 49 > 0 ⇒ ∆ = 7 0,25
1) Do đó phương trình có hai nghiệm là 3 7 x + = = 5 1 0,25 2 và 3 7 x − = = 2. − 2 0,25 2 Câu 2 (2,0 Cho phương trình 2
x − 4x +1 = 0 có hai nghiệm dương x , x . Không giải phương 1 2 điểm) x − x −8 3 1,0
trình, hãy tính giá trị của biểu thức 1 2 P = . x x + x x 1 2 2 1 2) x + x = 4
Vì phương trình có hai nghiệm x , x nên theo hệ thức Vi-ét ta có 1 2 1 2  . 0,25 x .x =  1 1 2 (x − x −8 3 1 2 )2 Ta có P = 0,25
x x ( x + x )2 1 2 2 1
(x + x )2 − 4x x −8 3 1 2 1 2 P = 0,25
x x x + x + 2 x x 1 2 1 2 1 2 2 4 − 4.1 −8 3 2 3 −8 3 6 − 3 = = = = − 3. 0,25 1. 4 + 2. 1 6 6
Hai đội công nhân cùng làm chung một công việc thì sau 15 ngày làm
xong. Nếu đội thứ nhất làm riêng trong 6 ngày rồi dừng lại và đội thứ
hai làm tiếp công việc đó trong 10 ngày thì cả hai đội hoàn thành được 1,5
50% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao nhiêu ngày mới
xong công việc trên ?
Gọi thời gian đội thứ nhất làm riêng xong công việc là x (đơn vị: ngày,
điều kiện: x > 0 )
Gọi thời gian đội thứ hai làm riêng xong công việc là y (đơn vị: ngày, 0,25
điều kiện: y > 0)
Trong 1 ngày đội thứ nhất làm được 1 (công việc), trong 1 ngày đội thứ hai làm x 0,25 được 1 (công việc). y
Hai đội cùng làm chung một công việc sau 15 ngày làm xong nên ta có 1) phương trình: 1 1 1 + = (1) 0,25 x y 15
Đội thứ nhất làm riêng trong 6 ngày và đội thứ hai làm tiếp công việc đó
trong 10 ngày thì cả hai đội hoàn thành được 50% công việc nên ta có phương trình: 6 10 1 + = (2) x y 2 0,25 1 1 1 + = x y 15 Câu 3
Từ (1) và (2) ta có hệ phương trình:  . 6 10 1 (2,0  + =  điểm)  x y 2
Giải hệ phương trình ta được x = 24  . 0,25 y = 40
Đối chiếu điều kiện và kết luận: Đội thứ nhất làm riêng thì sau 24 ngày xong
công việc, đội thứ hai làm riêng thì sau 40 ngày xong công việc. 0,25
Một thùng nước có dạng hình trụ với chiều cao 1,8m và đường kính đáy 1,2m.
Người ta sơn toàn bộ phía ngoài mặt xung quanh của thùng nước này (trừ hai 0,5
2) mặt đáy). Tính diện tích bề mặt được sơn của thùng nước đó (lấy π ≈ 3,14 ).
Diện tích bề mặt được sơn của thùng nước là S = 2π Rh 0,25 ≈ = ( 2 2.3,14.0,6.1.8 6,7824 m ). 0,25
Chứng minh CEHD là tứ giác nội tiếp. 1,5 A
Vì BE, AD là các đường cao của A ∆ BC nên  0,5 =  HDC HEC = 90° Câu 4 E (3,0 1) I
Xét tứ giác CEHD có  +  HDC HEC = 90° + 90° F O điểm) H = 180 . ° 0,25 B
Do đó CEHD là tứ giác nội tiếp. D C 0,25
Vẽ hình đúng được 0,5 điểm Chứng minh  =  DEH FEH và 1 1 2 + = . 1,0 DH DA DI
Vì CEHD là tứ giác nội tiếp nên  =  DEH DCH. 0,25
Xét tứ giác CEFB có  = 
CEB CFB = 90° nên CEFB là tứ giác nội tiếp nên  0,25 = 
FEH DCH. Từ đó suy ra  =  DEH FEH. 2) Vì  = 
DEH FEH nên EH là tia phân giác của góc DEF. Mà AE ⊥ EH nên AE
là tia phân giác ngoài của góc   DEF. Do đó HI AI EI = = 0,25 HD AD  DE    + − ⇒1 HI + +1 AI − = 2 DH HI DA AI ⇒ + = 2 DI DI ⇒ + = 2 DH DA DH DA DH DA 1 1 2 0,25 ⇒ + = . DH DA DI
Chứng minh đường thẳng AK luôn đi qua một điểm cố định khi A thay đổi. 0,5
Vì AFHE là tứ giác nội tiếp nên N  =  ⇒  =  AFE AHE BFK MHE A Mà    1  FBK HME sđ AN  = =  nên 2  E   K B ∆ FK FK BF BF ∽ M
∆ HE (g.g) ⇒ = = F O HE MH 2DH H
(do ta dễ dàng chứng minh được B D L 0,25 MH = 2DH ) (1) C Dễ thấy B ∆ FE ∽ DHE ∆ (g.g) M G FE BF ⇒ = (2) HE DH
Từ (1) và (2) suy ra FE = 2 FK HE HE Q
⇒ FE = 2FK ⇒ FK = KE. P
Gọi G là giao điểm thứ hai của AK và đường tròn (O); L là trung điểm của BC;
3) tiếp tuyến tại B, C của đường tròn (O) lần lượt cắt AK tại P và . Q Ta có ∆ ∽ ∆ ( . ) AF AC AF AC AEF ABC g g ⇒ = ⇒ = ⇒ A ∆ FK ∽ A
∆ CL ( .cg.c) EF BC FK LC ⇒  =  ⇒ ∆ ∽ ∆ ( . ) GB AG FAK CAL ABG ALC g g ⇒ = ⇒ G . B AC = A . G C . L CL AC Tương tự ∆ ∽ ∆ ( . ) AG GC AGC ABL g g ⇒ = ⇒ A . B GC = A . G BL = A . G C . L AB BL Từ đó suy ra . = . GB GC GB AC AB GC ⇒ = (3) AB AC 0,25 2 Ta có ∽ ( . ) PG PB BG PG  BG PBG PAB g g  ∆ ∆ ⇒ = = ⇒ = (4) PB PA AB PA  AB    2
Chứng minh tương tự ta có QG  CG  = (5) QA  AC   
Từ (3); (4) và (5) suy ra PG QG PG QG = ⇒ = hay PG QG = PA QA
PA − PG QA − QG AG AG
⇒ PG = QG ⇒ P ≡ .
Q Vì dây BC cố định nên điểm P cố định. Vậy đường thẳng
AK luôn đi qua điểm cố định P khi điểm A thay đổi.
x + 2 = (3y − 2x − )1( y +  )
Giải hệ phương trình 1  . 0,5
 3y − 2 + y + 2 = x + 3 + 2xy
Điều kiện xác định của hệ phương trình là 3y ≥ 2; x + 3 ≥ 0;3y − 2x −1≥ 0.
Biến đổi phương trình thứ nhất của hệ ta được 3( y + )
1 − (3y − 2x − )
1 = 2 (3y − 2x − ) 1 ( y + ) 1 .
Đặt a = 3y − 2x −1; b = y +1 (a > 0;b > 0) . Khi đó ta có phương trình 0,25 2 2
3b − a = 2ab ⇔ (a − b)(a + 3b) = 0 ⇔ a = . b
Do đó 3y − 2x −1 = y +1 ⇔ 3y − 2x −1= y +1⇔ y = x +1. Câu 5
Thay vào phương trình thứ hai ta được (0,5 2 2
3x +1 + 3 = x + 3 + 2x + x ⇔ 3x +1 − x + 3 = 2x + x − 3 điểm) 2x − 2
(x )( x ) (x ) 2 1 2 3 1  (2x 3) ⇔ = − + ⇔ − − + = 0 3x 1 x 3  3x 1 x 3  + + + + + +  Do 1 x ≥ − nên ta có 2 − (2x + 3) = 0 3 3x +1 + x + 3 0,25
⇔ (2x + 3)( 3x +1+ x +3) = 2 phương trình này vô nghiệm  
vì ( x + )( x + + x + ) 7 8 2 3 3 1 3 ≥ 0 +  > 2. 3  3   
Do đó từ phương trình trên ta được x =1, suy ra y = 2.
Vậy hệ phương trình đã cho có nghiệm duy nhất là ( x; y ) = ( 1;2 ). TỔNG ĐIỂM 10,0