Đề thi thử Toán vào lớp 10 lần 2 năm 2024 – 2025 phòng GD&ĐT Xuyên Mộc – BR VT

PHÒNG GIÁO DỤC & ĐÀO TẠO
KỲ THI THỬ TUYỂN SINH LỚP 10 THPT HUYỆN XUYÊN MỘC
LẦN 2, NĂM HỌC 2024-2025 MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
Ngày thi thử: 04/04/2024 Bài 1 (2,5 điểm). a) Giải phương trình 2 x + 7x + 6 = 0. 2x + 3y = 6
b) Giải hệ phương trình  .  2 − x + y = 2 2 c) Rút gọn biểu thức 2 A = 40 − 5 + ( 10 + 3)  5
Bài 2 (2,0 điểm). Cho hàm số 2
y = −x có đồ thị là (P). a) Vẽ (P).
b) Tìm m để đường thẳng (d): 2
y = 2x − m +1 cắt (P) tại hai điểm phân biệt có hoành độ
x , x thoả mãn 3 2 2
x + x x − 2x + 8 = 0 . 1 2 1 1 2 2 Bài 3 (1,5 điểm).
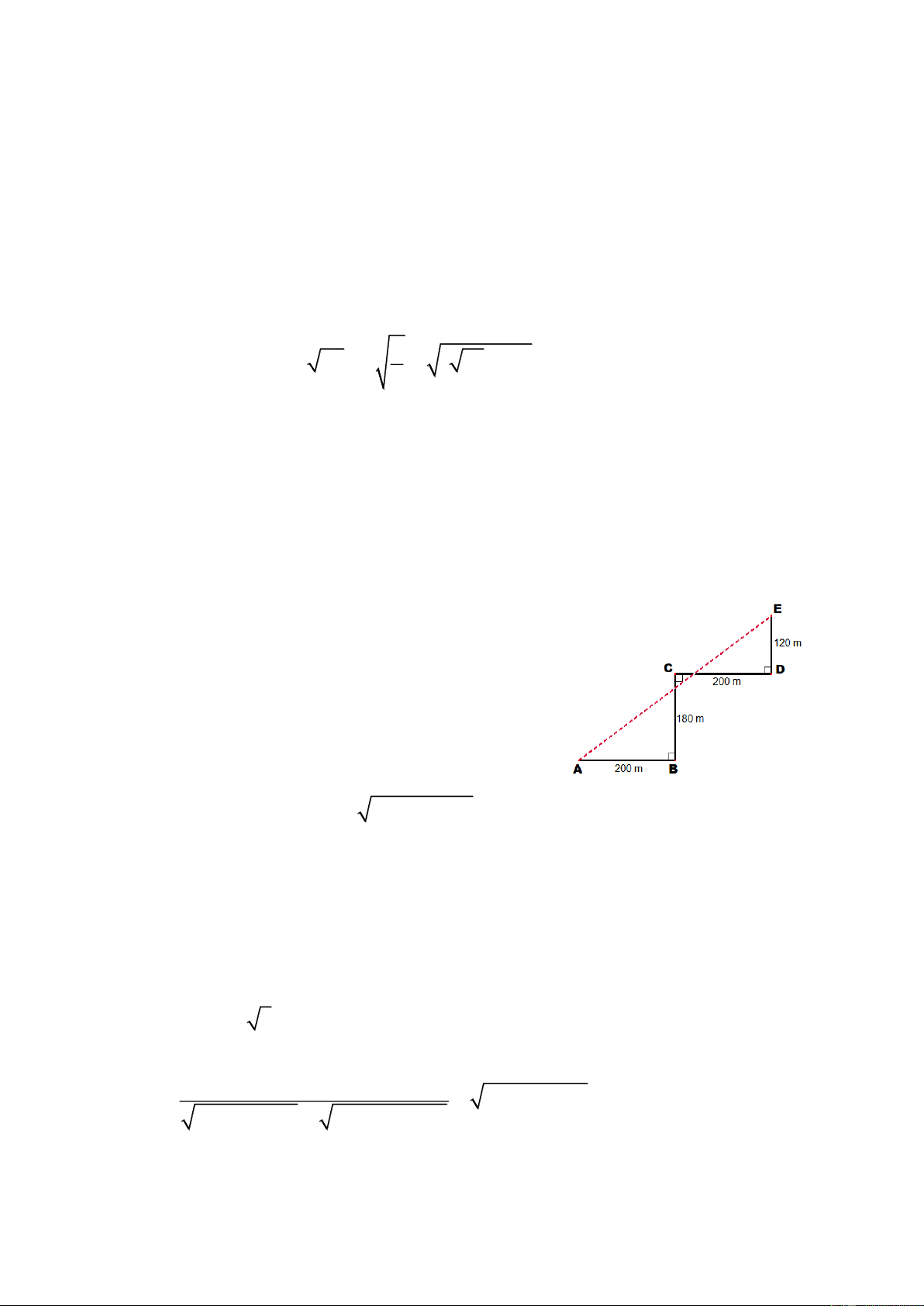
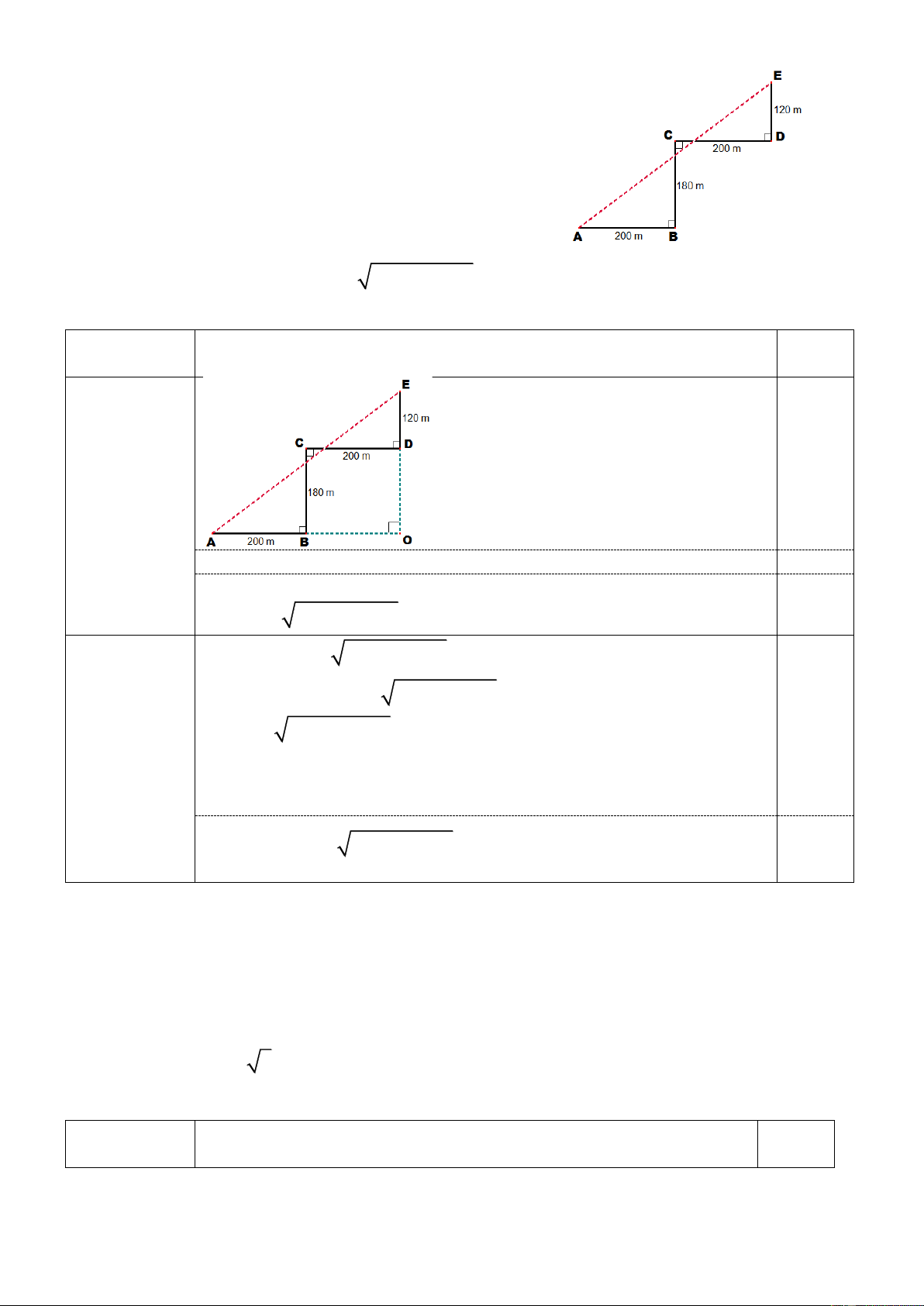
a) Một người ở vị trí A, đi về hướng Đông 200 m để
đến vị trí B, từ B đi về hướng Bắc 180 m để đến vị trí C,
từ C đi về hướng Đông 200 m để đến vị trí D, rồi từ D tiếp
tục đi về hướng Bắc 120 m để đến vị trí E. Tính khoảng
cách đường chim bay từ A đến E? (Hình vẽ bên). b) Giải phương trình 2
x(x −1) + 2x − 2x +1 = 1.
Bài 4 (3,5 điểm). Cho đường tròn (O; R), dây BC cố định không đi qua tâm O, điểm A di động
trên cung lớn BC sao cho AB < AC. Kẻ BE vuông góc AC tại E, kẻ CF vuông góc AB tại F, BE và CF cắt nhau tại H.
a) Chứng minh tứ giác AEHF nội tiếp.
b) Các đường thẳng EF, BC cắt nhau tại I. Chứng minh: IB.IC = IF.IE.
c) Kẻ đường kính AN của (O;R). Chứng minh HN luôn đi qua một điểm cố định khi A thay đổi.
d) Giả sử BC = R 3 . Tính diện tích hình tròn ngoại tiếp tam giác HEF theo R.
Bài 5 (0,5 điểm). Tìm giá trị lớn nhất của biểu thức 2024 2 M =
− 4x − 8x + 5. 2 2
4x + 4x +1 + 4x −12x + 9 ------ Hết ------
Họ và tên học sinh: ............................................................ Số báo danh: .....................................
Chữ kí của giám thị 1: ....................................................................................................................
PHÒNG GIÁO DỤC & ĐÀO TẠO
KỲ THI THỬ TUYỂN SINH LỚP 10 THPT HUYỆN XUYÊN MỘC
LẦN 2, NĂM HỌC 2024-2025 HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC MÔN: TOÁN Bài 1 (2,5 điểm). a) Giải phương trình 2 x + 7x + 6 = 0. 2x + 3y = 6
b) Giải hệ phương trình  .  2 − x + y = 2 2 c) Rút gọn biểu thức 2 A = 40 − 5 + ( 10 + 3)  5 Bài 1 Nội dung Điểm (2,5 điểm) a Tính đúng  = 25 0,25 (0,75đ)
Tìm được nghiệm x = 1 − ; x = 6 − 0,5 1 2 2x + 3y = 6 4y = 8 y = 2      0,5x2  2 − x + y = 2  2 − x + y = 2  2 − x + 2 = 2 b (0,75đ) x = 0   0,25 y = 2 c 2 0,5 (1,0đ) 2 A = 40 − 5
+ ( 10 + 3) = 2 10 − 10 + 10 + 3 5
2 10 − 10 + 10 + 3 = 2 10 + 3 0,5
Bài 2 (2,0 điểm). Cho hàm số 2
y = −x có đồ thị là (P). a) Vẽ (P).
b) Tìm m để đường thẳng (d): 2
y = 2x − m +1 cắt (P) tại hai điểm phân biệt có hoành độ
x , x thoả mãn 3 2 2
x + x x − 2x + 8 = 0 . 1 2 1 1 2 2 Bài 2 Nội dung Điểm (2,0 điểm) a
Xác định được 5 điểm khác nhau thuộc (P) hoặc thể hiện được trên 0,5 (1,0đ) đồ thị.
Vẽ đúng (P) trên mặt phẳng tọa độ Oxy 0,5 b PT hoành độ giao điểm 2 2
x + 2x − m +1 = 0 0,25 (1,0đ) 2 2
' = m  0  m  0; x + x = 2
− ; x .x = −m +1 0,25 1 2 1 2 3 2 2 2 2
x + x x − 2x + 8 = 0  x (x + x ) − 2x + 8 = 0 1 1 2 2 1 1 2 2 0,25 2 2 2  2
− x − 2x + 8 = 0  2
− (x + x ) + 4x x + 8 = 0 1 2 1 2 1 2 2  8
− − 4m + 4 + 8 = 0  m = 1  (tmđk m  0 ) 0,25 Bài 3 (1,5 điểm).
a) Một người ở vị trí A, đi về hướng Đông 200 m để
đến vị trí B, từ B đi về hướng Bắc 180 m để đến vị trí C,
từ C đi về hướng Đông 200 m để đến vị trí D, rồi từ D tiếp
tục đi về hướng Bắc 120 m để đến vị trí E. Tính khoảng
cách đường chim bay từ A đến E? (Hình vẽ bên). b) Giải phương trình 2
x(x −1) + 2x − 2x +1 = 1 Bài 3 Nội dung Điểm (1,5 điểm) 0,25 a (1,0đ) AO = 400 m, EO = 300 m 0,25x2 Tam giác AOE vuông tại O 2 2
 AE = 400 + 300 = 500m 0,25 2 2
pt  x − x + 2x − 2x + 1 = 1 2 2
 (2x − 2x +1) + 2 2x − 2x +1 − 3 = 0 0,25 Đặt 2
y = 2x − 2x +1, ( y  0) b (0,5đ)  = y 1 (n) Ta được pt: 2
y + 2 y − 3 = 0    y = 3 − (l) x = 0 Với y = 1 2 2
1 = 2x − 2x +1  2x − 2x +1 =1  0,25 x =1
Bài 4 (3,5 điểm). Cho đường tròn (O; R), dây BC cố định không đi qua tâm O, điểm A di động
trên cung lớn BC sao cho AB < AC. Kẻ BE vuông góc AC tại E, kẻ CF vuông góc AB tại F, BE và CF cắt nhau tại H.
a) Chứng minh tứ giác AEHF nội tiếp.
b) Các đường thẳng EF, BC cắt nhau tại I. Chứng minh: IB.IC = IF.IE.
c) Kẻ đường kính AN của (O;R). Chứng minh HN luôn đi qua một điểm cố định khi A thay đổi.
d) Giả sử BC = R 3 . Tính diện tích hình tròn ngoại tiếp tam giác HEF theo R. Bài 4 Nội dung Điểm (3,5 điểm) Hình vẽ (0,5đ)
Vẽ được (O) và 3 điểm A, B, C 0,25 Vẽ đúng 3 điểm E, F, H 0,25 0 AFH = AEH = 90 0,5 a
 tứ giác AEHF nội tiếp. 0,5 (1,0đ) = = 90O BFC BEC
Tứ giác BCEF nội tiếp. 0,25 b (1,0đ)  =   BEF FCB
IBE đồng dạng IFC 0,5  IB = IF  0,25 I .
B IC = IF.IE IE IC Ta có: = = 90O ABN ACN
(Chắn nửa đường tròn) c
 BH / /CN (cùng vuông góc với AC). 0,25 (0,5đ)
CH / / BN (cùng vuông góc với AB).
Do đó tứ giác BHCN là hình bình hành.
Suy ra HN đi qua trung điểm M cố định của đoạn BC cố định. 0,25 Ta có B  OM vuông tại M R 3 R 2 2 2 2 d
 OM = OB − BM = R − ( ) = 2 2 (0,5đ) 0,25 R
 AH = 2.OM = 2. = R 2
Do đó diện tích đường tròn ngoại tiếp AEF  là: 2 AH R .R 0,25 2 2 2  .r = .( ) =  .( ) = 2 2 4
Bài 5 (0,5 điểm). Tìm giá trị lớn nhất của biểu thức 2024 2 M =
− 4x − 8x + 5 2 2
4x + 4x +1 + 4x −12x + 9 Bài 5 Nội dung Điểm (0,5 điểm) 2 2 2 2
4x + 4x + 1 + 4x −12x + 9 = (2x + 1) + (2x − 3)
= 3 − 2x + 2x +1  3 − 2x + 2x +1 = 4 1 3 0,25
Dấu “=” xảy ra khi (3 − 2x)(2x +1)  0  −  x  2 2 2 2
− 4x − 8x + 5 = − (2x − 2) +1  1
− Dấu “=” xảy ra khi x =1 2024 2024 2 M =
− x + 4x + 40  −1= 505 2 2 − + + + + 4 x 2x 1 x 6x 9 Vậy MaxM = 50 0,25 5 khi x = 1 --------HẾT-------