Đề thi thử Toán vào lớp 10 lần 3 năm 2021 – 2022 trường Thái Thịnh – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi thử Toán vào lớp 10 lần 3 năm học 2021 – 2022 trường THCS Thái Thịnh, quận Đống Đa, thành phố Hà Nội; đề thi gồm 01 trang với 04 bài toán dạng tự luận, thời gian làm bài 90 phút (theo cấu trúc mới của sở GD&ĐT thành phố Hà Nội); đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm; kỳ thi được diễn ra vào thứ Sáu ngày 04 tháng 06 năm 2021. Mời bạn đọc đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
UBND QUẬN ĐỐNG ĐA
KÌ THI TUYỂN SINH VÀO LỚP 10 THPT
TRƯỜNG THCS THÁI THỊNH
NĂM HỌC 2021 – 2022 Môn thi: TOÁN
ĐỀ THI THỬ LẦN 3
Ngày thi: 04 tháng 6 năm 2021
Thời gian làm bài: 90 phút
Bài I (2.0 điểm) x 3 x 2 x 1 Cho hai biểu thức A và B với x 0;x 1 x x 1 x x
1) Tính giá trị biểu thức A khi x = 25.
2) Rút gọn biểu thức B. A 3) Cho P =
. Tìm tất cả các giá trị của x để 2
P −1 = 3P −1 . B
Bài II (2.5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một ô tô đi từ A đến B với vận tốc dự định. Quãng đường AB dài 48 km trong đó có
một đoạn đường qua khu dân cư dài 8km. Khi đi qua khu dân cư, xe phải giảm vận tốc
đi 10 km để đảm bảo an toàn. Tính vận tốc của ô tô khi đi qua khu dân cư biết rằng thời
gian ô tô đi từ A đến B là 1 giờ.
2) Một quả bóng đá tiêu chuẩn sử dụng tại các giải thi đấu chuyên nghiệp có đường kính
22cm. Khi quả bóng được bơm căng đúng tiêu chuẩn thì thể tích của quả bóng là bao nhiêu?
Bài III. (2.0 điểm) 2 + 2 y = 8 −
1) Giải hệ phương trình x 1 11 − 3 y = 2 x −1
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y 4x m 1 và parabol (P): 2
y x . Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm A(x ; y , B x ; y 1 1 ) ( 2 2)
thỏa mãn y + y = x x + 7 1 2 1 2
Bài IV. (3.5 điểm)
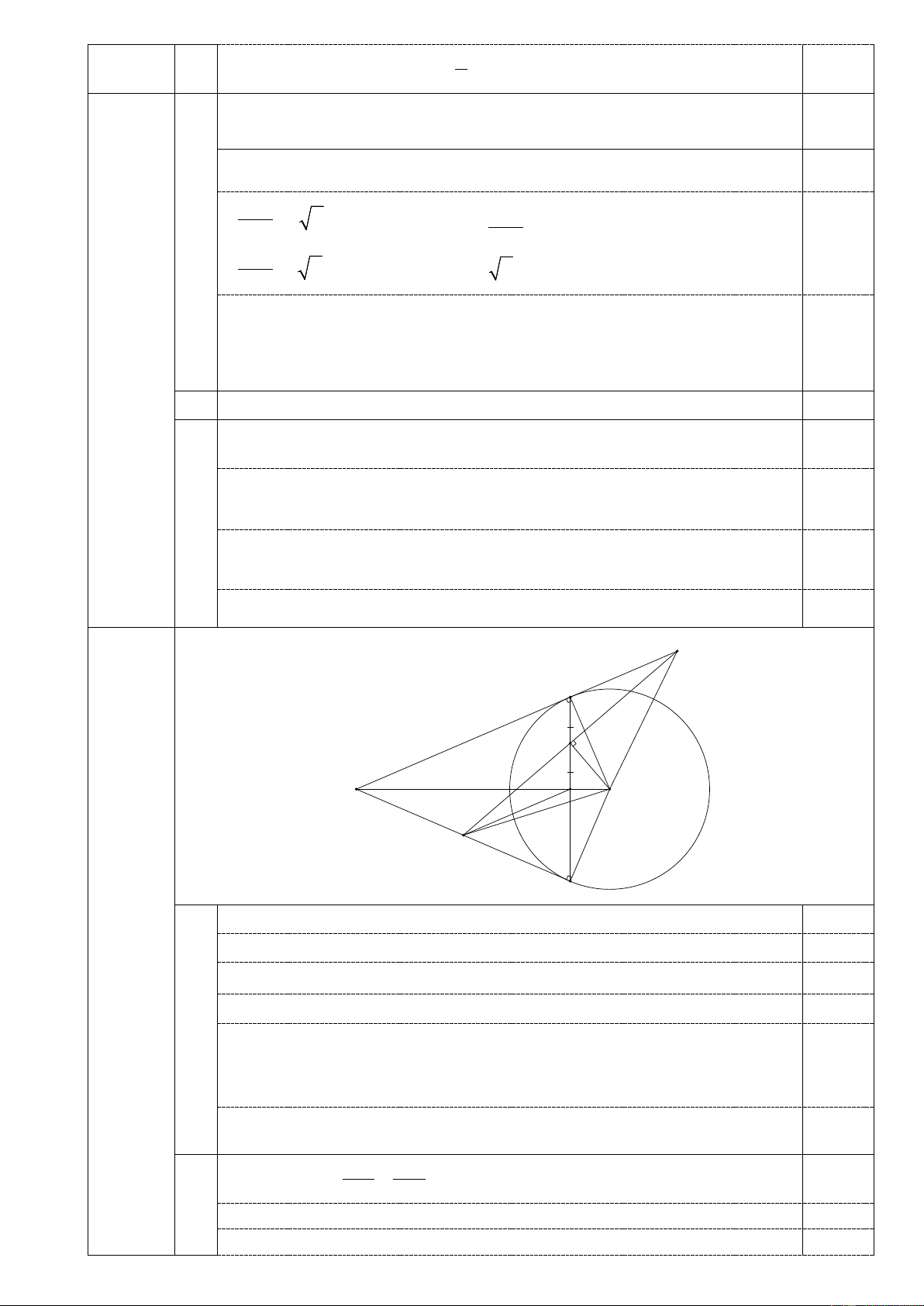
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn (O). Qua M kẻ hai tiếp tuyến
MA, MB tới đường tròn (O) (A và B là các tiếp điểm). MO cắt AB tại điểm H.
1) Chứng minh bốn điểm M, A, O, B cùng thuộc một đường tròn. AH MA 2) Chứng minh = . OA MO
3) Gọi K là trung điểm của AH. Đường thẳng vuông góc với OK tại K cắt tia MA tại điểm
C và cắt MB tại điểm D. Chứng minh góc OCK = góc OBA và D là trung điểm của MB.
............................. Hết .............................
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ………………………… Số báo danh:………………............................
Chữ kí của cán bộ coi thi số 1:…………...... Chữ kí của cán bộ coi thi số 2:........................
UBND QUẬN ĐỐNG ĐA KỲ THI THỬ LẦN 3
TRƯỜNG THCS THÁI THỊNH Ngày thi: 04/6/2021
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ THI THỬ LẦN 3 Bài Ý
Đáp án - Hướng dẫn chấm Điểm I
1) Tính giá trị của A… 0,50 (2,0 điểm)
Với x = 25 (TMĐK) ⇒ x = 5 0,25 Khi đó 8 A = . 0,25 5 2) Rút gọn B 1,0 x 2 x 1 B 0,25 x 1 x x x − 2 x +1 = 0,25 x ( x − ) 1 ( x − )2 1 = 0,25 x ( x − ) 1 x −1 B = 0,25 x 3) A Cho P =
. Tìm tất cả các giá trị của x để 2
P −1 = 3P −1 . 0,50 B 2 Đk: P −1≥ 0
, tìm được P=0 (loại); P=3 (tm) 0,25 3 P −1 ≥ 0 x 3 P
3 tìm được x = 9 (tmđk) 0,25 x 1 II
1) Giải bài toán bằng cách lập phương trình hoặc… 2,0 (2,5 điểm)
Gọi vận tốc ô tô khi đi qua khu dân cư là x (x>0; km/h) 0,25
Thời gian xe đi qua khu dân cư là 8 (h) 0,25 x
Vận tốc xe khi đi đoạn đường còn lại là x + 10 (km/h) 0,25 40
Thời gian xe đi trên đoạn đường còn lại là (h) 0,25 x +10
Vì tổng thời gian đi từ A đến B hết 1h nên ta có phương trình: 40 8 + = 0,25 1 x +10 x
Biến đổi và giải được x = 40 (tmđk); x= -2 (loại) 0,50
Trả lời vận tốc của xe ô tô khi đi qua khu dân cư là 40 km/h. 0,25 Lưu ý:
+ Nếu HS giải bài toán bằng cách lập HPT mà đúng, giám khảo vẫn cho điể m tối đa.
+ Nếu HS không giải PT mà ra KQ luôn thì trừ 0,25 điểm
2) Tính thể tích.... 0,5 Theo giả thiết, R = 11cm 0,25 4
Thể tích quả bóng là là 3 3 V =
π R ≈ 5572,5(cm ) 0,25 3 III 1) (2,0 điểm)
Giải hệ phương trình … 1,0
ĐKXĐ: x ≠1; y ≥ 0 0,25 2 + 2 y = 8 1 = x −1 1
, giải tìm được x −1 0,5 11 − 3 y = 2 = y 3 x −1 x = Từ đó: 2 (TM ) y = 9 0,25
Kết luận: S = {(2;9 } ) .
2) Cho parabol … 1,0 Pt hoành độ: 2
x − 4x + m −1 = 0 0,25
(d) cắt (P) tại hai điểm phân biệt: m<5 y=x2 nên 0,25
y + y = x x + 7 ⇔ x + x = x x + 7 ⇔ ( x + x )2 2 2 − 3x x − 7 = 0 1 2 1 2 1 2 1 2 1 2 1 2 x + x = 4 Áp dụng hệ thức Vi-ét 1 2 0,25 x x = m −1 1 2 (x + x )2 2
− 3x x − 7 = 0 ⇔ 4 − 3 m −1 − 7 = 0 , m = 4 (tmđk) 0,25 1 2 1 2 ( ) IV C (3,5 điểm) A K O M H D B
1 Chứng minh bốn điểm M, A, O, B cùng thuộc một đường tròn. 1,25
Vẽ hình đúng đến câu 1). 0,25 0 = 0 OAM 90 ;OBM = 90 0,25 Suy ra + 0 OAM OBM = 180 0,25 Tứ giác MAOB có + 0 OAM OBM = 180
Mà hai góc này là hai góc đố 0,25 i nhau
=> MAOB là tứ giác nội tiếp. Suy ra M, A, O, B cùng thuộc một đườ 0,25 ng tròn. 2 AH MA Chứng minh = 1,25 OA MO Chứng minh MA = MB 0,25 Chứng minh AB⊥OM 0,5 AH MA
Áp dụng hệ thức lượng trong tam giác vuông suy ra: = OA MO 0,5
3a Chứng minh góc OCK = góc OBA 0,5
Chứng minh OKAC nội tiếp suy ra = OCK OAK 0,25 Chứng minh = OBA OAK suy ra = OCK OBA 0,25
3b D là trung điểm của MB. 0,5 Chứng minh ∆DOC cân 0,25
Chứng minh ∆AKC=∆HKD suy ra DH//AC, từ đó suy ra D là trung điểm của MB. 0,25
Cán bộ chấm thi lưu ý:
- Điểm toàn bài để lẻ đến 0,25.
- Các câu hoặc các ý có cách làm khác với hướng dẫn ở trên nếu đúng vẫn được điểm tối đa của câu hay ý đó.
- Bài IV: Thí sinh vẽ sai hình trong phạm vi câu nào thì không tính điểm câu đó.