Đề thi thử Toán vào lớp 10 lần 3 năm 2022 trường THCS Ái Mộ – Hà Nội

UBND QUẬN LONG BIÊN
ĐỀ THI THỬ LẦN 3
TRƯỜNG THCS ÁI MỘ MÔN: TOÁN 9 NĂM HỌC: 2022 - 2023
Thời gian làm bài: 120 phút
Ngày kiểm tra: 26/5/2022 − Bài 1: (2 điểm): 3 x 3 1 1 Cho biểu thức M = và N = −
x  0 , x  1. x + x x −1 x x −1
a) Tính giá trị của biểu thức M khi x = 9 . b) Rút gọn biểu thức N .
c) Tìm các giá trị của x để biểu thức P = M.N có giá trị nguyên. Bài 2 (2,5 điểm):
1. Một quả bóng World Cup xem như một hình cầu có
đường kính là 17 cm . Tính diện tích mặt cầu và thể tích hình
cầu. (lấy   3,14 )
2. Giải bài toán sau bằng cách lập phương trình.
Một sân bóng đá theo chuẩn FIFA là sân hình chữ nhật,
chiều dài hơn chiều rộng 37 m và có diện tích 7140 m2.
Tính chiều dài và chiều rộng của sân bóng đá.  1 +3 y −2 = 5 x +1
Bài 3 (2 điểm): 1. Giải hệ phương trình  2  − 5 y − 2 = 1 −  x +1
2. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d ) : y = (2m + ) 1 x − 2 m + 4 và (P) 2 : y = x
a) Tìm chứng minh rằng: (d ) luôn cắt ( P) tại hai điểm phân biệt A , B .
b) Gọi H và K lần lượt là các hình chiếu vuông góc của A,B trên trục hoành. Tìm m để đoạn thẳng HK bằng 4? Bài 4 (3,0 điểm): Cho đường tròn ( ;
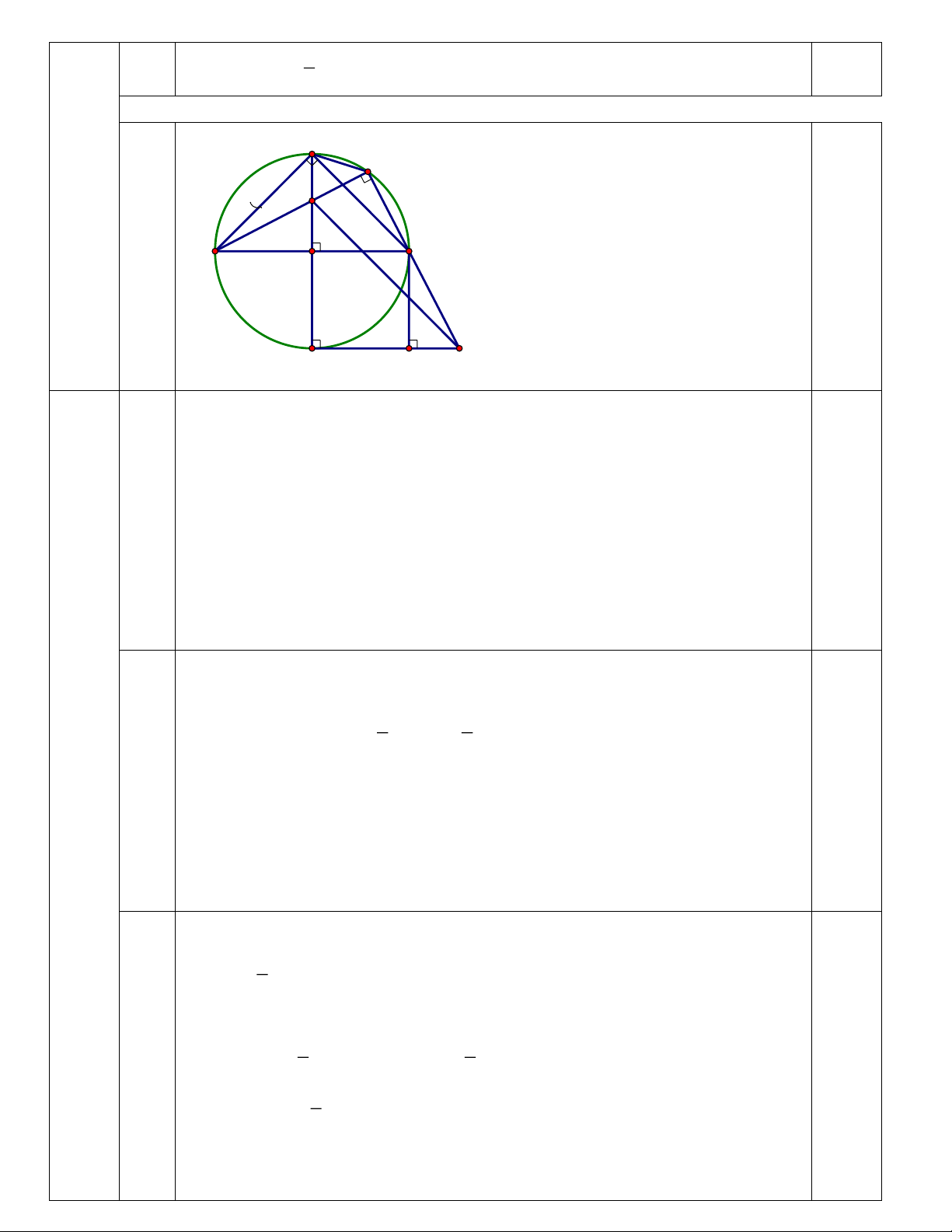
O R) đường kính AB . Kẻ đường kính CD vuông góc AB . Lấy điểm M thuộc cung
nhỏ BC , AM cắt CD tại E . Qua D kẻ tiếp tuyến với đường tròn (O) cắt đường thẳng BM tại N . Gọi
P là hình chiếu vuông góc của B trên DN .
1) Chứng minh bốn điểm M , N , D, E cùng nằm trên một đường tròn.
2) Chứng minh EN //CB 3) Chứng minh 2
AM .BN = 2R và Tìm vị trí điểm M trên cung nhỏ BC để diện tích tam giác BNC đạt giá trị lớn nhất.
Bài 5(0,5 điểm): Giải phương trình 2 2 16x +19x + 7 + 4 3
− x + 5x + 2 = (8x + 2)( 2− x + 2 3x +1) . ---Hết---
Chúc các con làm bài tốt!
TRƯỜNG THCS ÁI MỘ
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM BÀI Năm học: 2021 - 2022 THI THỬ LẦN 2 MÔN: TOÁN 9 Bài Câu Đáp án Biểu điểm Bài 1 a
a) Thay x = 9 (thỏa mãn điều kiện) vào biểu thức M ta có: 0,25 (2đ) 3 9 − 3 1 M = = 9 + 9 2 0,25 b
Điều kiện: x  0 ; x 1 1 1 1 1 0,5 b) N = − = − x −1 x x −1 x −1
( x − )1(x+ x + )1 x + x +1−1 x + x N = ( = 0,5 x − ) 1 ( x + x + ) 1
( x − )1(x+ x + )1 3( x − ) 3 x − 3 x + x 1
Ta có: P = M .N = . = x + x ( x − ) 1 ( x + x + ) 1
( x − )1(x+ x + )1 3 = x + x +1 2  1  3
Ta có 3  0 và x + x +1 = x + +  0  
với mọi x thuộc điều kiện xác định.  2  4 3   0  P  0 ( ) 1 x + x +1 3
Lại có: x  0  x + x  0  x + x +1  1   3  P  3(2) x + x +1 0,25 Từ ( )
1 và (2) ta có  0  P  3 mà P   P 1;  2 3 TH1: P = 1  =1 x + x +1
 x + x +1 = 3  x + x − 2 = 0  ( x + 2)( x − ) 1 = 0 
x −1 = 0  x = 1 ( T K MDK ) 3 TH2: P = 2 
= 2  2x + 2 x + 2 = 3  2x + 2 x −1= 0 x + x +1 2  1  1  3 1 3 − 0,25
2x + 2 x = 1  x + x =  x + =    x + = 2 3  x = 2  2  4 2 2 2 (TMĐK)  2 − 3  Vậy x  
 biểu thức P = M.N có giá trị nguyên.  2   Bài 2 1 Diện tích mặt cầu là: 2 2 2
.17 = 289 (cm )  907,46(cm ) 0,5 (2,5đ) Thể tích hình cầu là: 1 1 4913 3 3 3 2 V = .17 = .17 =
 (cm )  2571,136667(cm ) 0,5 6 6 6
Thiếu đơn vị đo ( cả 2 bước) trừ 0,25 đ 2
Gọi chiều dài của sân bóng đá là: x (m, x  37 ) 0,25
Chiều rộng của sân đá bóng là: x − 37 (m) 0,25
Vì diện tích sân bóng đá là 7140 m2 nên ta có phương trình:
x(x − 37) = 7140 0,25 2  x 3 − 7x − 7140 = 0 0,25
 (x −105)(x + 68) = 0  x −105 = 0 x =105(tm)     0,25 x + 68 = 0 x = 68 −  (loai)
Vậy: Chiều dài của sân bóng đá là 105 m 0,25
Chiều rộng của sân bóng đá là 105 − 37 = 68m. Bài 3 1  1 + 0, 5 3 y − 2 = 5 (2đ)   x +1  0, 5 (ĐKXĐ: x  1 − ; y  2 ) 2  − 5 y − 2 = 1 −  x +1 Đặ 1 t = ; a
y − 2 = b (b  0) thì hệ phương trình trở thành x +1 a + 3b = 5 2a + 6b = 10 a + 3b = 5 a = 2         2a − 5b = 1 − 2a − 5b = 1 − 11  b = 11 b  = 1  (TM )  1  1  1 − = 2  x +1 = x = (TM )   x +1   2   2   − =   − =  y 2 1 y 2 1 y = 3  (TM )  − 
Vậy phương trình có nghiệm ( x y) 1 ; = ;3   .  2  b
a) Xét phương trình hoành độ giao điểm của (d ) và ( P) có:
Pt hoành độ giao điểm của d và P: 2 0,25 x − (2m + )
1 x + 2m − 4 = 0 ∆= ( m − )2 2 1 +16 > 0 với mọi x 0,25
(d ) luôn cắt (P)tại 2 điểm phân biệt A và B với mọi m
Gọi x , x là các nghiệm của phương trình hoành độ giao điểm. 1 2
Theo hệ thức vi et ta có: x + x = 2m +1; x .x = 2m - 4 0,25 1 2 1 2 Bài 4
Ta có HK = x − x nên ( 2
(x + x ) - 4 x .x = 16 1 2 1 2 1 2 0,25 (3,0 Tìm được 1 m = và kết luận đ) 2 C M 0,25 E A B O D P N a
Xét đường tròn (O) có:
+ AMB = 90 (Góc nội tiếp chắn nửa đường tròn đường kính ABđường tròn) 0,25
+ DN là tiếp tuyến của (O) tại D  DN ⊥ OD (T/c tia tiếp tuyến của đường tròn)  ODN = 90 + Xét tứ giác MNDE có: 0,25
 EMN + NDE = 180 mà 2 góc này đối nhau
 Tứ giác MNDE là nội tiếp đường tròn 0,25
 bốn điểm M , N, D, E cùng nằm trên một đường tròn (ĐPCM) b
Xét đường tròn ngoại tiếp tứ giác EMND có:
DEN = DMN (2 góc nội tiếp chắn DN ) 1 Xét ( ;
O R) có: DMN = sđ 1 DB =
.90 = 45 (góc nội tiếp chắn DB ). 2 2 0,5  DEN = 45 O
 CB là tam giác vuông cân tại O  OCB = 45 .
Ta có: OCB = DEN (= 45) mà hai góc này ở vị trí đồng vị 0,5  DN //CB . c
Góc DNM là góc có đỉnh ở ngoài đường tròn (O) nên 1 DNM =
(sđ DM − sđ DB ). 2
Mà: sđ DB = sđ DA = 90 . 1 1 Nên: DNM =
(sđ DM − sđ DA ) = sđ AM . 2 2 1 Lại có: ABM =
sđ AM (góc nội tiếp chắn cung AM ) 2
Suy ra: DNM = ABM hay PNB = ABM . 0,25
Xét hai tam giác ABM và B  NP có: AMB = BPN (Cmt) ABM = PNB (Cmt) AM AB Suy ra: A  BM B
 NP (g − g) nên =
 AM.BN = A . B BP BP BN
Nhận thấy: OBPD là hình vuông nên BP = OD = R. Do đó: 2
AM .BN = A . B BP = 2 . R R = 2R . 0,25
Kẻ NK ⊥ BC tại K , EF ⊥ BC tại F . 1 0,25 S = NK.BC NBC 2
Do BC không đổi nên S max  NK max NBC
Mà ENKF là hình chữ nhật  NK max  EF max  0,25
E  0  M  B Câu 5 1 Điề u kiện: −  x  2 (0,5 3 đ)
Phương trình đã cho tương đương vớ i: ( x + )2 4
1 + (2 − x) + 4(3x + ) 1 + 2 2 . (2− x)(3x + ) 1 = 2 (4x + )
1 ( 2 − x + 2 3x +1) ( x + )2 4
1 + (2 − x) + 4(3x + ) 1 + 2 2 . (2− x)(3x+ ) 1 − 2(4x + ) 1 2 − x − 2 2 . (4x + ) 1 3 x +1 = 0  2 − x = a 
Đặt 2 3x +1 = b(a,b  0) . Phương trình đã cho trở thành 4x +1= c  2 2 2
c + a + b + 2ab − 2ac − 2bc = 0  (a + b − c)2 = 0  a + b − c = 0 0,25
Thay trở lại ta có phương trình 2 − x + 2 3x +1 − (4x + ) 1 = 0
 2 − x + 2 3x +1 − 4x −1 = 0  ( 2− x − )
1 + (2 3x +1 − 4) − 4(x − ) 1 = 0 2 − x −1 4(3x + ) 1 −16  + − 4(x − ) 1 = 0 2 − x +1 2 3x +1 + 4 1− x 12( x − ) 1  + − 4(x − ) 1 = 0 2 − x +1 2 3x +1 + 4 (  −   x − ) 1 12 1 + − 4 = 0  
 2 − x +1 2 3x +1 + 4 
 x =1 ( thỏa mãn). 1 − 12  1  Do + − 4  0, x   − ;2   2 − x +1 2 3x +1 + 4  3  0,25
Vậy nghiệm của phương trình là x = 1.
Ban giám hiệu duyệt Tổ trưởng duyệt Người ra đề Nguyễn Ngọc Sơn Hồ Mai Thúy Nguyễn Thị Hòa