PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 HUYỆN GIAO THUỶ
THPT KHÔNG CHUYÊN NĂM HỌC 2024 - 2025 Môn thi: Toán ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút)
Đề khảo sát gồm 02 trang.
Phần I. Trắc nghiệm (2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng
trước phương án đó vào bài làm. 2 3x
Câu 1. Điều kiện xác định của biểu thức là x 1 A. x  1. B. x  0 hoặc x  1. C. x  1. D. x  0.
Câu 2. Cho đường thẳng d  : y  mx  2  m đi qua điểm A2; 
1 . Hệ số góc của đường thẳng d  bằng A. 1. B. 1. C. 2. D. 2.  x y  m
Câu 3. Hệ phương trình     có nghiệm  ;
x y (2; 1) . Giá trị m  n bằng x 2y  n  A. ( 2
 ;1). B. 4 . C. 5. D. 4.
Câu 4. Giá trị của tham số m để hàm số 2 y  2( m 1
 )x đồng biến khi x  0 là
A. m  1. B. m  1 . C. 0  m  1. D. m  0.
Câu 5. Trong các phương trình sau đây, phương trình nào có 2 nghiệm âm phân biệt? A. 2 x 2x 1 0 . C. 2 x  2x 2024  0 . B. 2 x 3x 1 0 . D. 2 x 7  0 .
Câu 6. Một hộp sữa có dạng hình trụ với đường kính đáy 7, 4 cm
và chiều cao 8 cm . Với mỗi một hộp sữa, để ghi các thông tin của
sản phẩm nhà sản xuất đã dán giấy xung quanh hộp sữa (như
hình bên). Hỏi để dán 10.000.000 hộp sữa phải cần ít nhất bao
nhiêu m2 giấy để dán xung quanh hộp sữa (lấy   3,14 và bỏ qua
diện tích rìa và mép dán) A. 2 371776 m . B. 2 185888 m . C. 2 92944 m . D. 2 59200 m .
Câu 7. Cho đường tròn O, R , có 2 tiếp tuyến với O tại hai điểm A và B cắt nhau tại M thỏa mãn  0
AMB  60 . Tính độ dài đoạn thẳng MO theo R được kết quả là R 3 A. 3R . B. R 3 . C. 2R . D. . 2
Câu 8. Cho hình nón có bán kính đáy bằng 3cm, chiều cao bằng 4cm. Diện tích xung
quanh của hình nón đã cho là A.   2 24 cm  . B.  2 15 cm  . C.  2 12 cm  . D.  2 30 cm  . Trang 1/2
Phần II. Tự luận (8 điểm) Bài 1. (1,5 điểm) 1
1) Chứng minh đẳng thức 2 ( 2 3)   4 . 32 2 x  2  x  4 2 
2) Rút gọn biểu thức A   1   với x  0, x  4 . x  2  x  4 x  2  Bài 2 (1,5 điểm).
Trong mặt phẳng tọa độ Oxy, cho parabol P 2
: y  x và đường thẳng d  : y  mx  4 .
1) Chứng minh d  luôn cắt P tại hai điểm phân biệt với mọi giá trị của m .
2) Gọi các toạ độ giao điểm của d  và P là x ; y và  x ; y . Tìm tất cả các giá 2 2  1 1  trị của x x y y m để 1 2 1 2     2 . x x x x 2 1 1 2  2 x  2y  1  x
Bài 3 (1,0 điểm). Giải hệ phương trình   1 2 2  x  4y 1 4 xy  .  2    x  Bài 4 (3,0 điểm).
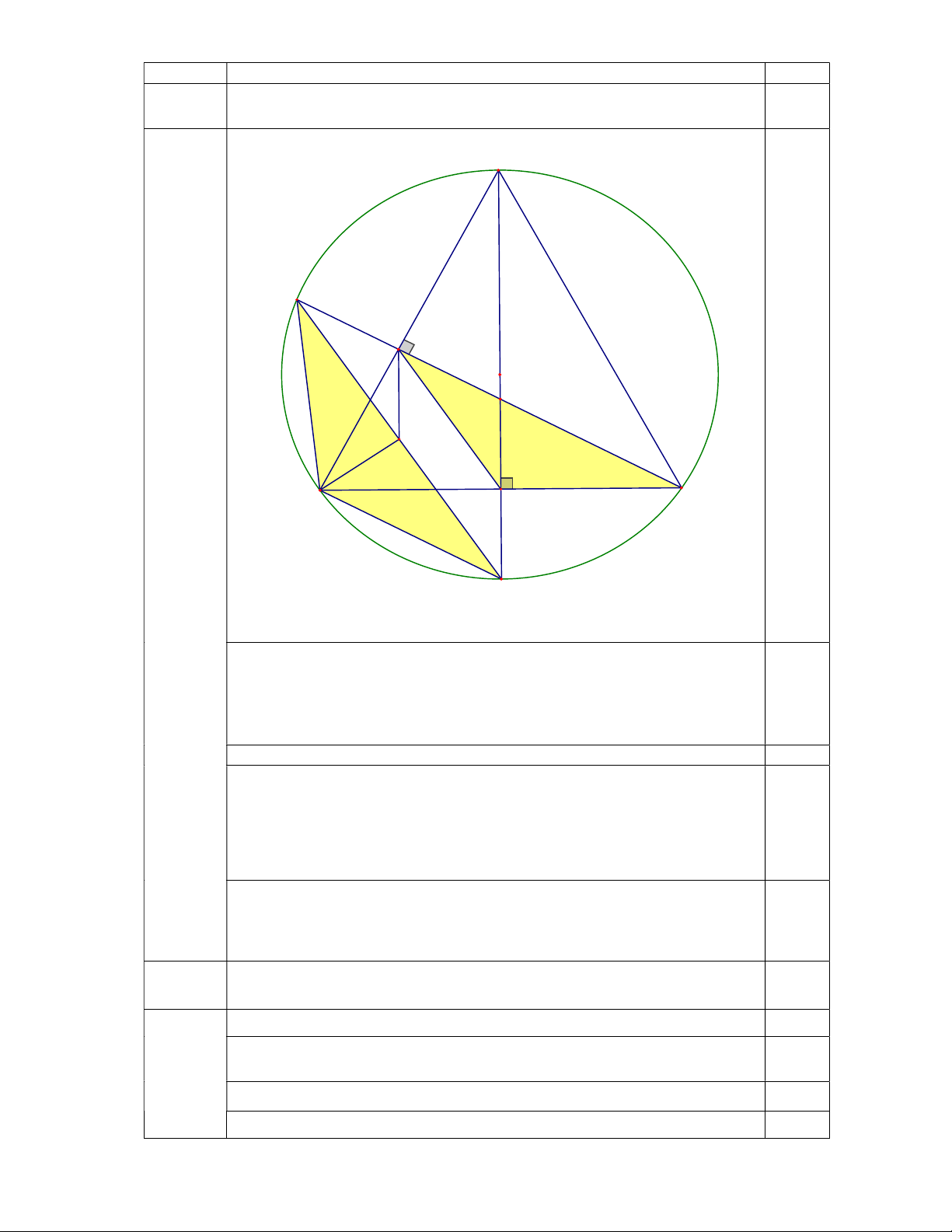
1) Cho ABC vuông tại A có AB  10 cm, B  0
B  60 . Vẽ nửa đường tròn O có đường kính O
BC (hình vẽ bên). Tính diện tích ABC và tính
diện tích phần được tô đậm trong hình vẽ (kết quả
làm tròn đến hàng đơn vị). C A
2) Cho tam giác ABC cân tại A nội tiếp đường tròn O và  0 BAC  90 . Kẻ CE
vuông góc với AB tại E , tia CE cắt O tại điểm thứ hai là K . Kẻ đường kính AD của
O , gọi I là giao điểm của AD với BC .
a) Chứng minh bốn điểm ,
A E, I ,C cùng thuộc một đường tròn và tam giác BKD
đồng dạng với tam giác IEC .
b) Từ E kẻ đường thẳng vuông góc với BC cắt KD tại M . Chứng minh tứ giác
EMDI là hình bình hành và MB  I . D Bài 5 (1,0 điểm). 1) Giải phương trình 2
x  x  1 x 1  3x  2x x .
2) Xét hai số thực dương a và b thỏa mãn a  b  2. Chứng minh rằng 4 5   ab   . 2 2 a  b  2 ab
--------------- HẾT ---------------
Họ và tên thí sinh: ……………………………………… Họ tên, chữ ký GT 1:……………………….
Số báo danh: …………………………………………….... Họ tên, chữ ký GT 2:……………………… Trang 2/2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM HUYỆN GIAO THUỶ
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10
THPT KHÔNG CHUYÊN NĂM HỌC 2024 - 2025 Môn thi: Toán
Phần I. Trắc nghiệm (2 điểm) Câu 1 2 3 4 5 6 7 8 Đáp án B A C C B B C B
Phần II. Tự luận (8 điểm) Bài Nội dung Điểm 1
Bài 1.1) Chứng minh đẳng thức: 2 ( 2 3)   4 . 0,5 32 2 1 1 Biến đổi vế trái: 2 ( 2 3)   2 3  3 2 2  0,25 2  2 1 1  3 2 
 3 2  2 1 4 VP . 2 1  0,25
Vậy đẳng thức được chứng minh. x  2  x  4 2 
Bài 1.2) Rút gọn biểu thức A   1,   với x  0, x  4 . 1,0 x  2  x  4 x  2 
Với x  0, x  4 , ta có:  2   x   x   x  x   x 2 2 4 2 2 4  0,25 A 1        1   x  2  x  4 x  2  x  2  x  4 x  4    x  2  x  2 x     1 0,25 x  2  x 4      x 2 x x 2    0,25 x   1 2  x  4 x 2  1  . x  2 x  2 0,25 2 Vậy A  . x  2
Trong mặt phẳng tọa độ Oxy, cho parabol P 2
: y  x và đường thẳng Bài 2  1,5 d  : y  mx  4 .
Bài 2.1) Chứng minh d  luôn cắt  P tại hai điểm phân biệt với mọi giá trị của m 0,5
Xét phương trình hoành độ giao điểm: 2 x  mx  4 2  x  mx  4  0(1) 0,25 Do . a c  0, m   . R
 phương trình luôn có hai nghiệm phân biệt m 0,25
 d  luôn cắt P tại hai điểm phân biệt với mọi giá trị của m .
Gọi các toạ độ giao điểm của d  và P là  x ; y và  x ; y . Tìm tất 2 2  1 1  Bài 2.2) x x y y 1,0
cả các giá trị của m để 1 2 1 2     2 . x x x x 2 1 1 2 Điều kiện: x .x  0 1 2
Vì toạ độ giao điểm của d  và P là  x ; y và  x ; y nên 2 2  1 1  2 2 y  x ; y  x 1 1 2 2
Vì x ; x là hoành độ giao điểm nên cũng là nghiệm của phương trình (1) 1 2  b x  x    m  0,25 1 2 
Theo định lý Vi-ét ta có: a  c x x   4 1 2  a  x x  x x x  x  2x x m  8 1 2 1 2  1 2 2 2 2 2 Ta có: 1 2        x  x   m 1 2  x x x x x x 4  0,25 2 1  1 2 1 2 2 m  8 Theo đề bài có được  m  2. 4  0,25
Tìm được m  0; m  4
Đối chiếu điều kiện và kết luận: m  0; m  4 . 0,25  2 x  2y  1  x Bài 3
Giải hệ phương trình  1,0  1 2 2  x  4y 1 4 xy   2    x 
Điều kiện: x  0, y    2  2 x  2y  1 x  2 y  1  x    x    0,25  1 2 2  4 x  4y 1 4 xy     x  2y  1  0 2  2 2   x   x 2  2  4 4  1 
1  0   2  x  2   (thoả mãn điều kiện) 0,25 2  x  x x
Thay vào phương trình thứ nhất được y  1. 0,25
Vậy hệ phương trình có nghiệm  ; x y  2;  1 . 0,25
Bài 4.1 Cho ABC vuông tại A có AB   0 10 cm, B  60 . ….. 1,0 Có ABC vuông tại A AC 10 3 0
 AC  AB.tan 60  10 3 cm, BC    20 cm 0 sin 60 3 0,25 2 1 
Diện tích tam giác vuông ABC là 2 S  .10.10 3 50 3 cm 0,25 ABC 2 2 1  BC  1
Diện tích nửa hình tròn đường kính BC là 2  .  .100.  50 cm   0,25 2  2  2 Diện tích cần tìm là 2 50  50 3  70 cm .
Nếu học sinh lấy   3,14 , làm tròn không đúng kết quả, toàn bài trừ 0,25 điểm 0,25 Bài 4.2 Chứng minh bốn điểm ,
A E, I ,C cùng thuộc một đường tròn và tam giác Bài 4.2a) 1,0
BKD đồng dạng với tam giác IEC A K E M B I C D Ta có 
AIC  90 (vì AD là đường kính nên là đường trung trực của BC )
suy ra I thuộc đường tròn đường kính AC 0,25 và có 
AEC  90 (vì CE  AB tại E)
suy ra E thuộc đường tròn đường kính AC
Suy ra bốn điểm A, E, I, C cùng thuộc một đường tròn 0,25
Do tứ giác AEIC nội tiếp, suy ra  IEC   IAC (cùng chắn cung  CI ) Xét O , ta có  BKD   DKC vì cung  BD bằng  DC 0,25 Mà  DKC   DAC (cùng chắn cung  DC ) Suy ra  BKD   IEC (1) Xét O , ta có  BDK   BCK (cùng chắn cung  BK ) 0,25 Hay  BDK   ICE (2)
Từ (1) và (2) suy ra  EIC∽  KBD. Bài
b) Từ E kẻ đường thẳng vuông góc với BC cắt KD tại M . Chứng minh 1,0 4.2b)
tứ giác EMDI là hình bình hành và MB  I . D Chỉ ra  EIA   ECA   KDA  KD//EI 0,25
Chỉ ra EI //MD; EM //ID suy ra tứ giác EMDI là hình bình hành và 0,25 ME  I . D Ta có EM //AD   BEM   BAD( 
 BKD) nên tứ giác EMBK nội tiếp 0,25   MEB   MKB   MKE=
MBE  MEB cân suy ra MB  ME  I . D 0,25
Bài 5.1) Giải phương trình 2
x  x  1 x 1  3x  2x x . 0,5 ĐKXĐ: 0  x 1 2
x  x  1 x 1 3x  2x x 0,25
 x  1x  x 1x 2x x12x 0 x 1 x x 3 1 x4x   12x 0 1 x  x 1 x  2x x
x 12x 12x 2 2x  x   1  
12x 0 12x  0 1 x  x 1 x  2x x 2         x x 2x x 1 1 2   1 0,25   0  1x  x 1 x  2x x  2 x 2x  x 1 ( vì  1>0). 1 x  x 1 x  2x x 1
 x  (thỏa mãn ĐKXĐ). 2
Xét hai số thực dương a và b thỏa mãn a  b  2 . Bài 5.2) 4 5 Chứng minh rằng   ab   . 0,5 2 2 a  b  2 ab x y   2 2 2 x y
Áp dụng bất đẳng thức:   với a,b  0 a b a  b 0,25 2 2 4 5  2 1  9 Ta có: A    ab     ab 2 2  2 2  a  b  2 ab  a  b  2 2ab  2ab 2 2 1  1  7  A    ab  2 2   a  b  2ab  2  ab  2ab 9 7 9 7   2      2 a  b2  2 2ab 4  2 2ab 0,25 a b2 Lại có: ab   3 7 1  A   2   7 4 2 2
Dấu bằng xảy ra khi: a  b  1. Chú ý:
+ Thiếu hoặc sai đơn vị trừ 0,25 điểm/lỗi; toàn bài không trừ quá 0,5 điểm.
+ Điểm toàn bài là tổng điểm của các câu không làm tròn.
+ Học sinh làm cách khác đúng cho điểm tương đương.
Document Outline

• 1. Chính thức-Đề thi thử Toán 9 lần 3 năm học 23-24.
• 2. Chính thức-Đáp án đề thi thử Toán 9 lần 3 năm học 23-24