Đề thi thử Toán vào lớp 10 năm 2021 – 2022 trường THCS Nguyễn Công Trứ – Hà Nội

TRƯỜNG THCS NGUYỄN CÔNG TRỨ
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2020 - 2021
Thời gian làm bài: 90 phút Bài 1. (2,0 điểm) Cho hai biểu thức sau: x 1  x  3 5 4  A  và B      (với x  0 ; x 1) x 1  x 1 1 x x 1    1 a) Tìm x để A  . 2 b) Rút gọn B . c) Cho P  .
A B . Tìm x để P có giá trị là số nguyên. Bài 2 (2,5 điểm).
1. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai trường A và B có tổng số 460 học sinh tham gia kỳ thi vào lớp 10 THPT; kết quả, cả hai trường
có 403 học sinh thi đỗ. Riêng trường A số học sinh thi đỗ chiếm tỉ lệ 85%, riêng trường B số học
sinh thi đỗ chiếm tỉ lệ 90%. Tính số học sinh tham gia kỳ thi vào lớp 10 THPT của mỗi trường?
2. Một tháp nước có bể chứa là một hình cầu, đường kính bên trong của bể chứa đo được là 6 (mét).
Người ta dự tính lượng nước đựng đầy trong bể đủ cung cấp cho một khu dân cư trong 5 ngày. Biết
khu dân cư đó có 1570 người. Hỏi người ta đã dự tính trung bình mỗi người dùng bao nhiêu lít nước trong một ngày?
(Lấy   3,14 ; kết quả làm tròn đến chữ số thập phân thứ nhất) Bài 3. (2,0 điểm)  2  x  2x  3y  5
1. Giải hệ phương trình:  2   2 x  2x  3y  8 2. Cho phương trình: 2 x  2m  
1 x  4  0 (m là tham số)
a) Chứng minh phương trình luôn có hai nghiệm phân biệt x ; x 1 2
b) Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn x  x  5 1 2
Bài 4. (3,0 điểm) Cho đường tròn O , hai đường kính AB và CD vuông góc nhau. Gọi M là điểm chuyển
động trên cung nhỏ AC . Gọi I là giao điểm của BM và CD . Tiếp tuyến tại M của O cắt tia DC tại K .
a) Chứng minh tứ giác AMIO nội tiếp được. b) Chứng minh  MIC   MDB và  MKD  2. MBA c) Tia phân giác 
MOK cắt BM tại N . Chứng minh CN vuông góc BM .
d) Gọi E là giao điểm của DM và AB . Chứng minh diện tích tứ giác IEDB không đổi.
Bài 5. (0,5 điểm) Cho x  0; y  0 thỏa mãn x  y  xy  8 . 1
Tìm giá trị lớn nhất của biểu thức: M   xy 4 4 x  y ---HẾT---
NHÓM GIÁO VIÊN TOÁN HÀ NỘI https://www.facebook.com/groups/650500558651229/ HƯỚNG DẪN Bài 1. (2,0 điểm) Cho hai biểu thức sau: x 1  x  3 5 4  A  và B      (với x  0 ; x 1) x 1  x 1 1 x x 1    1 a) Tìm x để A  . 2 b) Rút gọn B . c) Cho P  .
A B . Tìm x để P có giá trị là số nguyên. Hướng dẫn 1 a) Tìm x để A  . 2 1 x 1 1 x 1 1 2 x  2  x 1 x  3 Để A       0     x 1 x 1 2 x   0 1 2 x   0 2 2 2 1 Vì 2 x   1  0 x
 tmdk , do đó: x  3  0  x  3  x  9
Kết hợp điều kiện: x  0 ; x  1 1 Vậy 0  x  , 9 x  1 để A  . 2 b) Rút gọn B . x  3 5 4 B    x 1 1 x x 1 x  3 5 4 B    x 1 x 1  x   1  x   1
 x 3 x  15 x  14 B   x  1 x  1
x  x  3 x  3  5 x  5  4 B   x  1 x  1 x  7 x  6
B   x  1 x  1  x  1 x 6
B   x  1 x  1 x  6 B  x 1 x  6 Vậy B  (với x  0 ; x  1). x 1 c) Cho P  .
A B . Tìm x để P có giá trị là số nguyên. x 1 x  6 x  6 5 Ta có: P  . A B  .   1 x 1 x 1 x 1 x 1 5
Vì x  0  x  0  x 1  1  0  1  1 5  P  6 ( * ) * x 1 5  0  5 5 Ta thấy:    0  1  1  P  1 ( ) * x 1  0 x  tmdk  x 1 x 1 
NHÓM GIÁO VIÊN TOÁN HÀ NỘI https://www.facebook.com/groups/650500558651229/
Từ (*) và (**)  1  P  6 mà P    P 2;3;4;5;  6 Ta có bảng: P 2 3 4 5 6 3 2 1 x 4 0 2 3 4 9 4 1 x 16 0 4 9 16 Nhận TM TM TM TM TM xét  9 4 1  Vậy x  1
 6; ; ; ;0 để P có giá trị là số nguyên.  4 9 16  Bài 2 (2,5 điểm).
1. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai trường A và B có tổng số 460 học sinh tham gia kỳ thi vào lớp 10 THPT; kết quả, cả hai trường
có 403 học sinh thi đỗ. Riêng trường A số học sinh thi đỗ chiếm tỉ lệ 85%, riêng trường B số học
sinh thi đỗ chiếm tỉ lệ 90%. Tính số học sinh tham gia kỳ thi vào lớp 10 THPT của mỗi trường?
2. Một tháp nước có bể chứa là một hình cầu, đường kính bên trong của bể chứa đo được là 6
(mét). Người ta dự tính lượng nước đựng đầy trong bể đủ cung cấp cho một khu dân cư trong 5
ngày. Biết khu dân cư đó có 1570 người. Hỏi người ta đã dự tính trung bình mỗi người dùng bao
nhiêu lít nước trong một ngày?
(Lấy   3,14 ; kết quả làm tròn đến chữ số thập phân thứ nhất) Hướng dẫn
1. Gọi số học sinh tham gia kỳ thi vào lớp 10 THPT của hai trường A và B lần lượt là x; y học sinh.  ; x y  N;0  ; x y  460
Vì hai trường A và B có tổng số 460 học sinh tham gia kỳ thi cào 10 nên ta có phương trình: x  y  460  1
Số học sinh thi đỗ của trường A là 85%.x  0,85x (học sinh)
Số học sinh thi đỗ của trường B là 90%.y  0,9y (học sinh)
Vì hai trường có 403 học sinh thi đỗ nên ta có phương trình: 0,85x  0,9y  403 2 x  y  460
Từ (1) và (2) ta có hệ phương trình:  0,85x  0,9y  403
Giải hệ phương trình ta được: x  220; y  240 (thỏa mãn ĐK)
Vậy số học sinh tham gia kỳ thi vào lớp 10 THPT của trường A là 220 học sinh và của
trường B là 240 học sinh.
2. Bán kính bên trong của bể chứa là: 6:2=3 (m) 4 4
Thể tích của lượng nước bên trong khi bể đầy là: 3 3
V   R  .3,14.3  113,04 3 m  3 3
Trung bình mỗi ngày một người dùng số mét khối nước là:      3 113, 04 : 5 1570 0,0144 m 
Đổi 0, 0144 14, 4l
Vậy trung bình mỗi ngày một người dùng 14,4 (lít) nước. Bài 3. (2,0 điểm)  2  x  2x  3y  5
1. Giải hệ phương trình:  2   2 x  2x  3y  8 2. Cho phương trình: 2 x  2m  
1 x  4  0 (m là tham số)
a) Chứng minh phương trình luôn có hai nghiệm phân biệt x ; x 1 2
b) Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn x  x  5 1 2 Hướng dẫn
NHÓM GIÁO VIÊN TOÁN HÀ NỘI https://www.facebook.com/groups/650500558651229/  2  x  2x  3y  5 1. Ta có  2   2 x  2x  3y  8 3
  2x 2x  3   2  x  2x  3y  5 2 x  2x  1   1   3y  5   x  2 1  0   3  y  6 x 1  0   y  2 x  1    y  2
Vậy nghiệm của hệ phương trình là  ; x y  1;2 2. 2 x  2m   1 x  4  0
a) Ta có   m  2 ' 1  4 Vì m  2 1  0 với mọi m  m  2 1  4  0 với mọi m   '  0 với mọi m
Vậy phương trình luôn có hai nghiệm phân biệt x ; x 1 2
b) Ta có phương trình luôn có hai nghiệm phân biệt x ; x (cmt) 1 2 x  x  2 m 1 1 2   Theo Viet ta có:  x .x  4   1 2 +) x  x  5 1 2 2 2  x  2 x .x  x  25 1 1 2 2
  x  x 2  2x .x  2 x .x  25 1 2 1 2 1 2  4.m  2 1  8  8  25  4m  2 1  9  m  2 9 1  4 3 3  TH1: m 1  TH2: m 1  2 2 5 1  m   m  2 2 5 1 
Vậy để phương trình có hai nghiệm phân biệt thỏa mãn x  x  5 thì m   ; 1 2  2 2
NHÓM GIÁO VIÊN TOÁN HÀ NỘI https://www.facebook.com/groups/650500558651229/
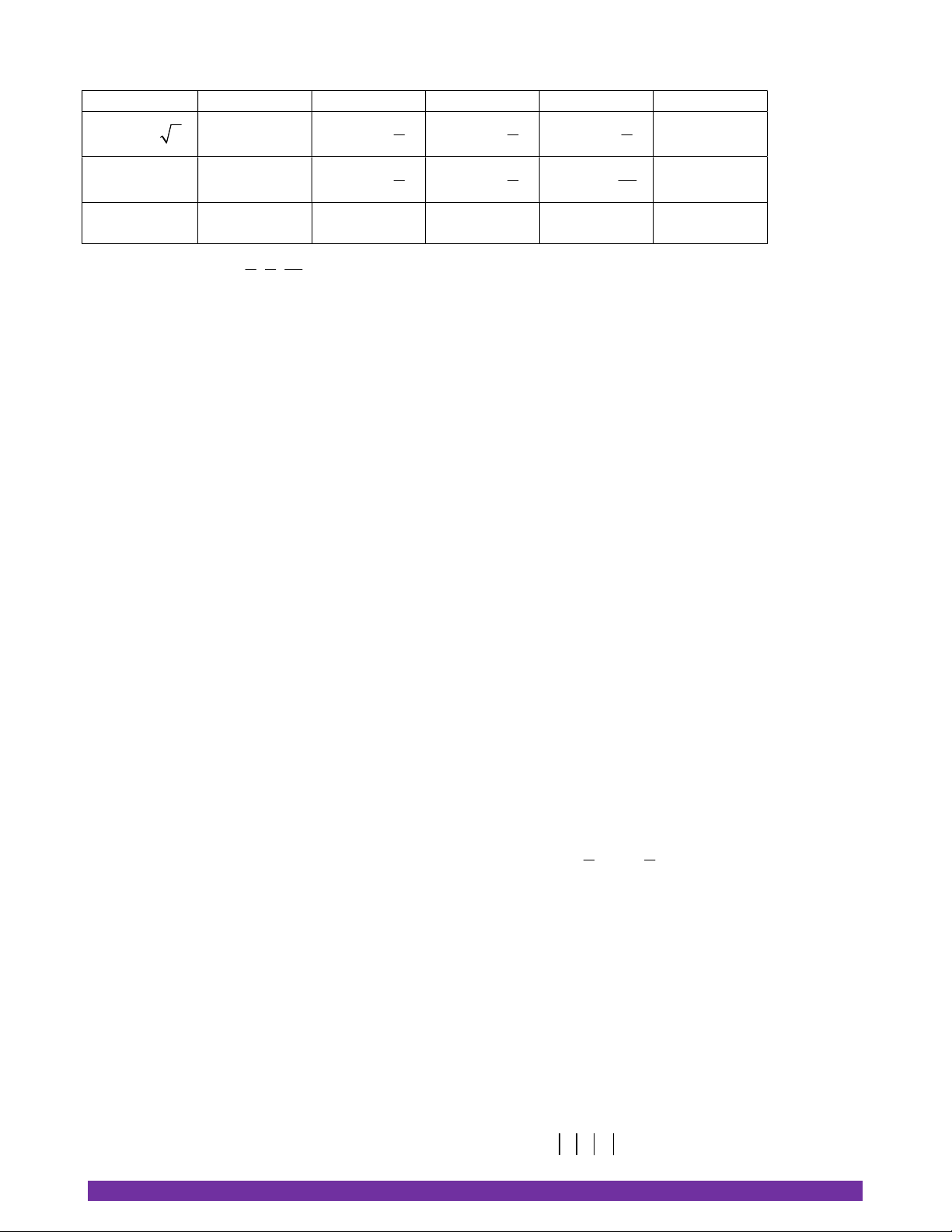
Bài 4. (3,0 điểm) Cho đường tròn O , hai đường kính AB và CD vuông góc nhau. Gọi M là điểm chuyển
động trên cung nhỏ AC . Gọi I là giao điểm của BM và CD . Tiếp tuyến tại M của O cắt tia DC tại K .
a) Chứng minh tứ giác AMIO nội tiếp được. b) Chứng minh  MIC   MDB và  MKD  2. MBA c) Tia phân giác 
MOK cắt BM tại N . Chứng minh CN vuông góc BM .
d) Gọi E là giao điểm của DM và AB . Chứng minh diện tích tứ giác IEDB không đổi. Hướng dẫn
a) Chứng minh tứ giác AMIO nội tiếp được. K C M I A B O D Ta có: 
AMB  90 (góc nội tiếp chắn nửa đường tròn)
AB  CD tại O ( giả thiết)   AOI  90 Tứ giác AMIO có  AMB  
AOI  180 , mà hai góc ở vị trí đối nhau
 AMIO là tứ giác nội tiếp. b) Chứng minh  MIC   MDB và  MKD  2. MBA K C M I A B O D Ta có:  MIC   MAB (cùng bù với  MIO )  MAB  
MDB (hai góc nội tiếp cùng chắn cung MB ) Do đó:  MIC   MDB
Ta có: MK là tiếp tuyến tại M của đường tròn O   OMK  90  O  MK vuông tại M   MKD   MOK  90  AOM   MOK  90 Do đó:  MKD   MOA (cùng phụ với  MOK )   1 Mặt khác:  MOA  2.
MBA (góc nội tiếp và góc ở tâm cùng chắn cung AM ) 2
NHÓM GIÁO VIÊN TOÁN HÀ NỘI https://www.facebook.com/groups/650500558651229/ Từ   1 và 2   MKD  2. MBA c) Tia phân giác 
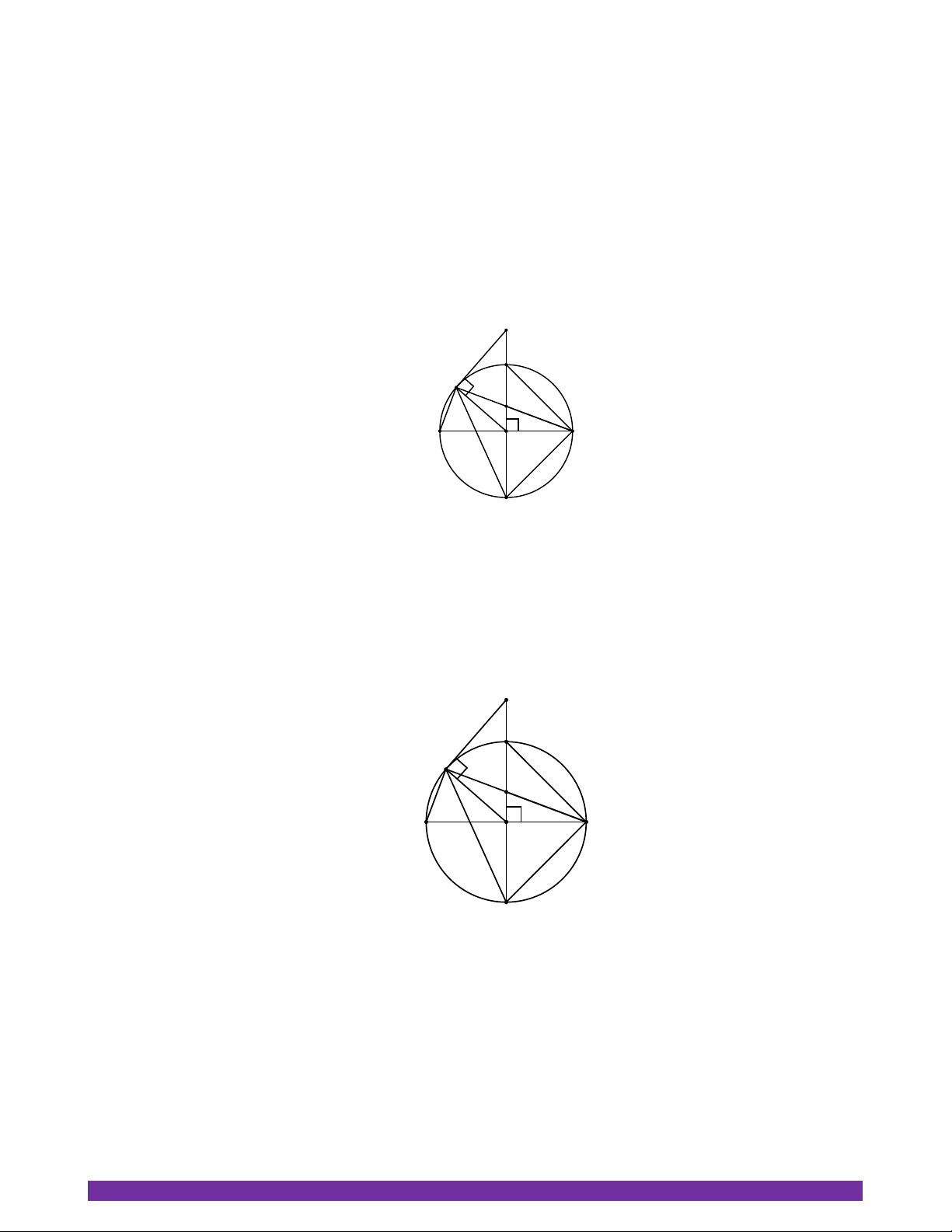
MOK cắt BM tại N . Chứng minh CN vuông góc BM . K C M N I A B O D 1 Ta có:  CBN   CDM  sđ 
MC (hai góc nội tiếp cùng chắn một cung) 3 2 Tia phân giác 
MOK cắt BM tại N (giả thiết)   1 CON   1 COM  sđ  MC ( 
COM là góc ở tâm chắn cung  MC ) 4 2 2
Từ 3 và 4   CBN  
CON , mà hai góc ở hai đỉnh kề nhau trong tứ giác BCNO   CNB  
COB  90 (hai góc nội tiếp cùng chắn một cung)  CN  BM
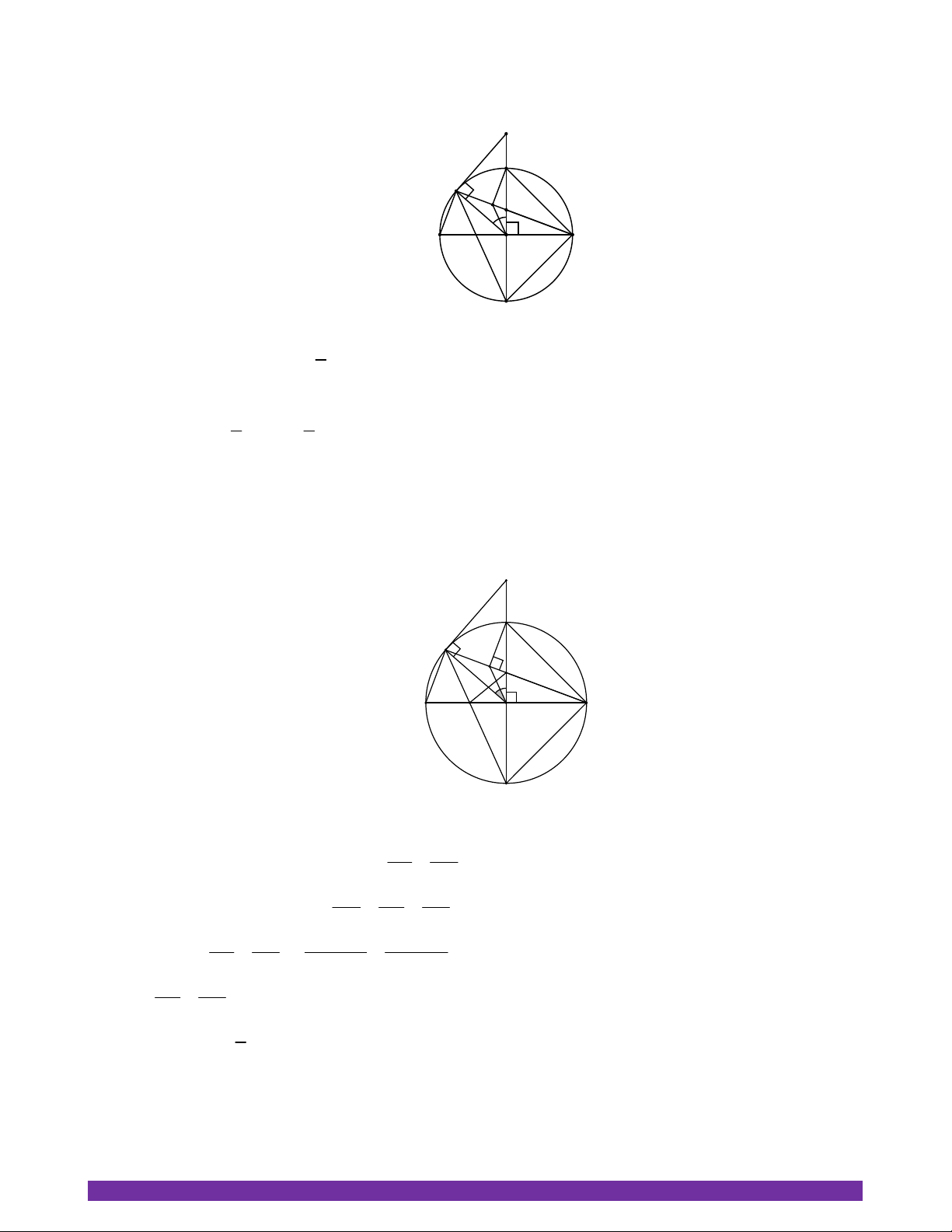
d) Gọi E là giao điểm của DM và AB . Chứng minh diện tích tứ giác IEDB không đổi. K C M N I A B E O D Ta có AB  CD   AD   BD   AME  
EMB (hai góc nội tiếp chắn hai cung bằng nhau)  EB MB ME là tia phân giác  AMB   EA MA MB OB OD O  BI ∽ M  BA (g-g)    vì OB  OD  R MA OI OI EB OD EB OD Suy ra:   
(tính chất dãy tỉ số bằng nhau) EA OI EA  EB OI  OD EB OD 2   E . B DI  A . B OD  2R AB DI 1 Mà 2 S  E . B DI  2R IEDB 2
Vậy diện tích tứ giác IEDB không đổi.
NHÓM GIÁO VIÊN TOÁN HÀ NỘI https://www.facebook.com/groups/650500558651229/
Bài 5. (0,5 điểm) Cho x  0; y  0 thỏa mãn x  y  xy  8 . 1
Tìm giá trị lớn nhất của biểu thức: M   xy 4 4 x  y Hướng dẫn
Ta có x  0; y  0  x  y  2 xy dấu bằng xảy ra khi và chỉ khi x  y Từ 2
x  y  xy  8  xy  8  (x  y)  8  2 xy  ( xy 1)  9  xy 1  3  xy  4 Lại có 2 2
x  y  xy  8  x  y 1  9  xy  (x  y 1)  (9  xy) 2 2 2 2 2 2 2 2 2
 x  y 1 2(x  y  xy)  (9  xy)  x  y 1 2.8  (9  xy)  x  y 17  (9  xy) Mà 2
xy  4  9  xy  5  (9  xy)  25 và 2 2 x y  16 Do đó 2 2 2 2 2 2 2 4 4 2 2
x  y 17  25  x  y  8  (x  y )  64  x  y  64  2x y  64  2.16  32 1 1 1 1 1 129 129 Suy ra    xy   4   xy   M  4 2 4 2 4 2 x  y 32 x  y 32 x  y 32 32 y  x
dấu bằng xảy ra khi và chỉ khi   x  y  2(tmdk) x  y  xy  8 129 Vậy M 
khi và chỉ khi x  y  2 . max 32
____________________ HẾT ____________________
NHÓM GIÁO VIÊN TOÁN HÀ NỘI
https://www.facebook.com/groups/650500558651229/