Đề thi thử Toán vào lớp 10 năm 2021 – 2022 trường THPT Hàm Rồng – Thanh Hóa

TRƯỜNG THPT HÀM RỒNG
KỲ THI THỬ VÀO LỚP 10 THPT NĂM HỌC 2021 - 2022 ĐỀ CH ÍNH THỨC Môn: TOÁN
Thời gian làm bài: 120 phút
Đề thi gồm 01 trang
(Không kể thời gian giao đề)
Ngày thi: 18 tháng 4 năm 2021
Câu 1: (2,0 điểm) x  x  x  x  Cho biểu thức: 2 11 1 3 P    (với x  0 ). x  4 x  3 x  3 x 1
1. Rút gọn biểu thức P.
2. Tính giá trị của biểu thức P khi x  3 2 2 .
Câu 2: (2,0 điểm)
1. Tìm m để đường thẳng y   2
m  2 x 1 m song song với đường thẳng y  2x  3 .  x  y 
2. Giải hệ phương trình: 2 5  3
 x  2y  3 
Câu 3: (2,0 điểm) 1. Giải phương trình 2 2x  5x  2  0 .
2. Cho phương trình: 2     2 x
2m 1 x  m 1  0 (1), (x là ẩn số).
Tìm m để phương trình (1) có hai nghiệm phân biệt x    1,x2 thỏa mãn:  x x 2 x 5x 1 2 1 2
Câu 4: (3,0 điểm)
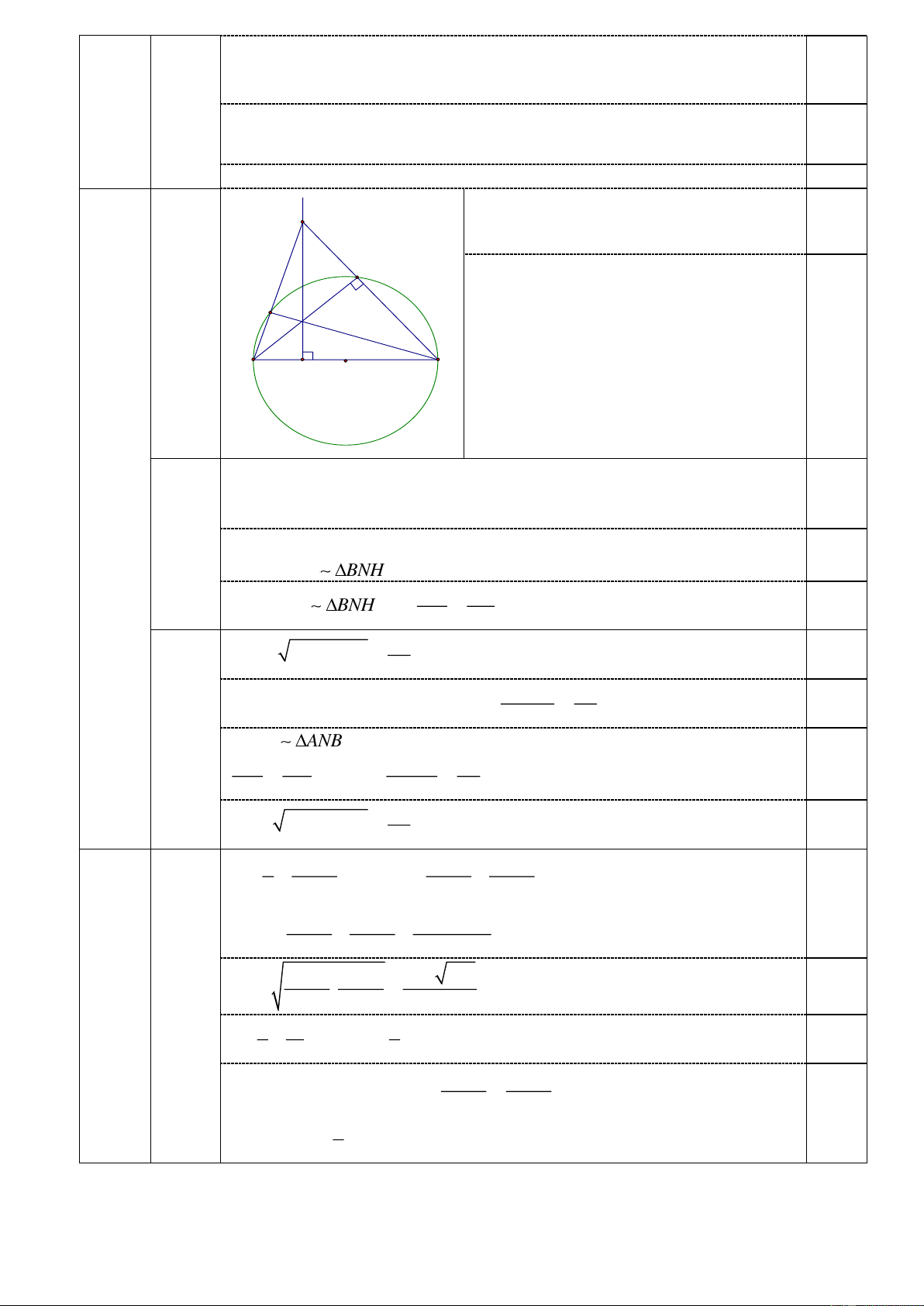
Cho đường tròn (O) đường kính AB  2R . Gọi I là trung điểm của AO và d là đường
thẳng vuông góc với AB tại I . Gọi M là một điểm tùy ý trên d sao cho M nằm ngoài (O) ,
MB cắt (O) tại điểm N  N  B , MA cắt (O) tại điểm P  P  A . Đường thẳng AN cắt d tại H .
1. Chứng minh rằng: BNHI là tứ giác nội tiếp.
2. Chứng minh rằng: H . P HB  H . A HN
3. Giả sử MI  2R . Tính IH theo R .
Câu 5: (1,0 điểm) Cho a là số thực dương. Tìm giá trị nhỏ nhất của biểu thức: 4 a 2 T    a  3a . 2 a a  4 ----- Hết -----
Họ và tên thí sinh: .................................................................................... Số báo danh: .......................................................
Chữ ký giám thị 1: ............................................................... Chữ ký giám thị 2: ............................................................... TRƯỜNG THPT HÀM RỒNG
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC Môn: TOÁN
Hướng dẫn chấm này gồm 02 trang Hướng dẫn chung:
Nếu học sinh giải cách khác với cách nêu trong HDC này, mà đúng, thì vẫn được điểm
tối đa của phần (câu) tương ứng. Điể Câu Ý
Lời giải (vắn tắt) m 1 1
Với điều kiện x > 1 thì : (2,0đ) (1,0đ)
x  2 x 1 1(x 1)(x 9) x  2 x  3 P     x   3  x   1
 x  3 x  1 0,5
 x  3 x  1 x 1    . x   3  x   1 x 1 0,5 2
x  3  2 2   2  2      (1,0đ) 1 x 2 1 2 1. 0,5 x 1  2  11 2 2 Khi đó: P      . x   2   1 2 1 1 1 2 0,5 2 1
Đường thẳng y   2
m  2 x 1 m song song với đường thẳng
(2,0đ) (1,0đ) y  2x 3 2 m  2  2   1   m  3 0,5 2 m  4 m  2       m  2 m  2  m  2  0,5 2
2x  y  5
4x  2y 10 (1,0đ)    3
 x  2y  3  3
 x  2y  3  0,25 7  x  7  
2x  y  5 0,25 x 1   y  3  0,25
Vậy hệ phương trình có 1 nghiệm (x; y)  (1; 3  ) 0,25 1 2
  5 16  9  0    3 0,5 3
(1,0đ) Phương trình có hai nghiệm phân biệt là (2,0đ)       b 1 b x   , x   2 1 2 2a 2 2a 0,5 2
 = (2m + 1)2 – 4(m2 – 1) = 5 + 4m
(1,0đ) Phương trình có hai nghiệm phân biệt 5
   0  m   (*) 4 0,25 x  x  2  m 1 Áp dụng hệ thức Vi 1 2 -ét, ta có:  2 x x  m 1  1 2
Theo giả thiết: x  x 2  x  5x 1 2 1 2
 x  x 2  4x x  x  x  6x 1 2 1 2  1 2 2 0,25 1   2  m  2 1  4 2 m   1  2
 m 1 6x  6m  6  6  x 2 2  x  m 1 2 Vì x  x  2m  1 x  m 1 2 1 2 2
x x  m 1  m(m 1)  m 1  m  1  1 2 0,25
Kết hợp với điều kiện  m  1
 là giá trị cần tìm. 0,25 4 1 d
Do AB là đường kính nên 0 ANB  90 (3,0đ) (1,0đ) M Do
d vuông góc với AB nên 0 HIB  90 0,5 N
=> Tứ giác BNHI có tổng 2 góc đối bằng 0
180 nên là tứ giác nội tiếp P H B A I O 0,5 2
Trong tam giác MAB có các đường cao: MI, AN, BP.
(1,0đ) Mặt khác H là giao điểm của MI và AN nên H là trực tâm. Suy ra B, H, P thẳng hàng. 0,25
Các tam giác vuông APH  và B
 NH có PHA  NHB (đối đỉnh) nên A  PH B  NH 0,5 HP HA Vì A  PH B  NH nên   H . P HB  H . A HN HN HB 0,25 3 5R 2 2    (1,0đ) MB MI BI 2 0,25 MI.AB 8R 2.S
 AN.MB  MI.AB  AN   MAB MB 5 0,25 A  IH A
 NB (Vì là các tam giác vuông có góc A chung) AH AI AI.AB 5R   AH   AB AN AN 8 0,25 3R 2 2 HI  AH  AI  8 0,25 5 2 4 a a  4 a 2 2 (1,0đ)         T a 3a a 4a 2 2 a a  4 a a  4  15 a a  2 2 a  4 4  2  T     a  4a 2 16a a  4 16a 0,25 2 2 a  4 a 15.2 4a T  2 . 
 a  22  4 2 16a a  4 16a 0,25 1 15 1    4  T  2 4 4 0,25 2 
Dấu đẳng thức xảy ra khi a 4 a 2 
, a  4, a  2  0  a  2 . 2 16a a  4 Vậy 1 min T  khi a  2 . 4 0,25 2