Đề thi thử Toán vào lớp 10 năm 2022 – 2023 trường THCS Nguyễn Thị Định – BR VT

UBND HUYỆN LONG ĐIỀN
ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT
TRƯỜNG THCS NGUYỄN THỊ ĐỊNH
NĂM HỌC 2022 – 2023 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (Đề thi gồm 01 trang) Ngày thi: 22/04/2022 Bài 1: (3,5 điểm) a) Giải phương trình: 2
x  3x  2  0 ìï2x - 3y = -5
b) Giải hệ phương trình: ïí ï3x + 4y = 18 ïî
c) Rút gọn biểu thức :     2 6 A 2 3  75 2  3 d) Giải phương trình: 2
x  5  x  10x  2x 1 Bài 2: (2,0 điểm) Cho parabol (P): 2
y  x và đường thẳng (d): y  mx  m  2 (Với m là tham số)
a) Vẽ (P) và đường thẳng (d) trên cùng một hệ trục tọa độ khi m=1.
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt parabol (P) tại hai điểm
phân biệt có hoành độ x , x thỏa mãn x  x 1 1 2 1 2 Bài 3: (0,5 điểm)
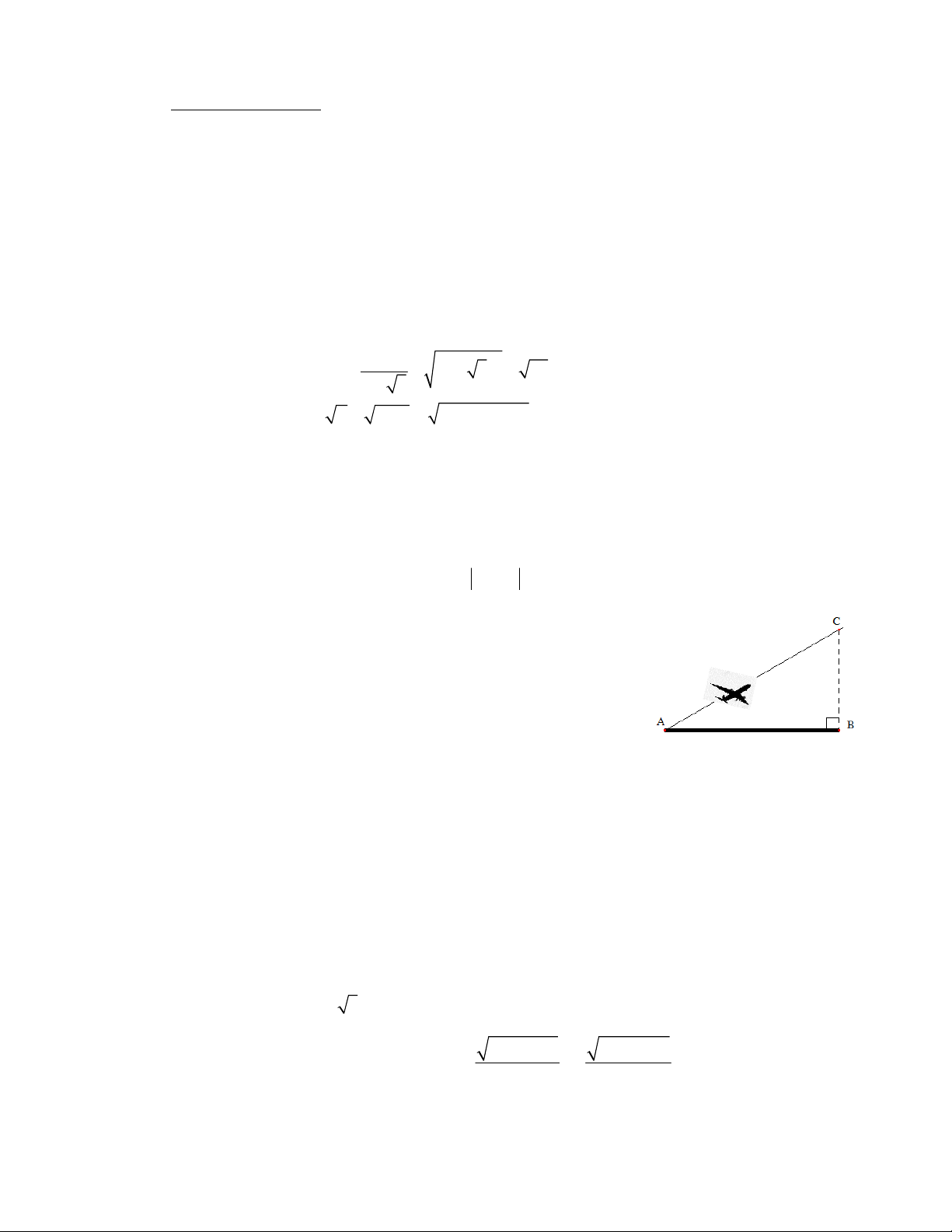
Một máy bay phản lực cất cánh từ vị trí A ( như hình vẽ )
bay lên với một góc 300 so với đường băng có phương nằm
ngang, sau một thời gian 30 giây máy bay đạt được độ cao
3000 mét so với đường băng. Tính vận tốc trung bình của
máy bay trong trường hợp này (làm tròn đến hàng đơn vị).
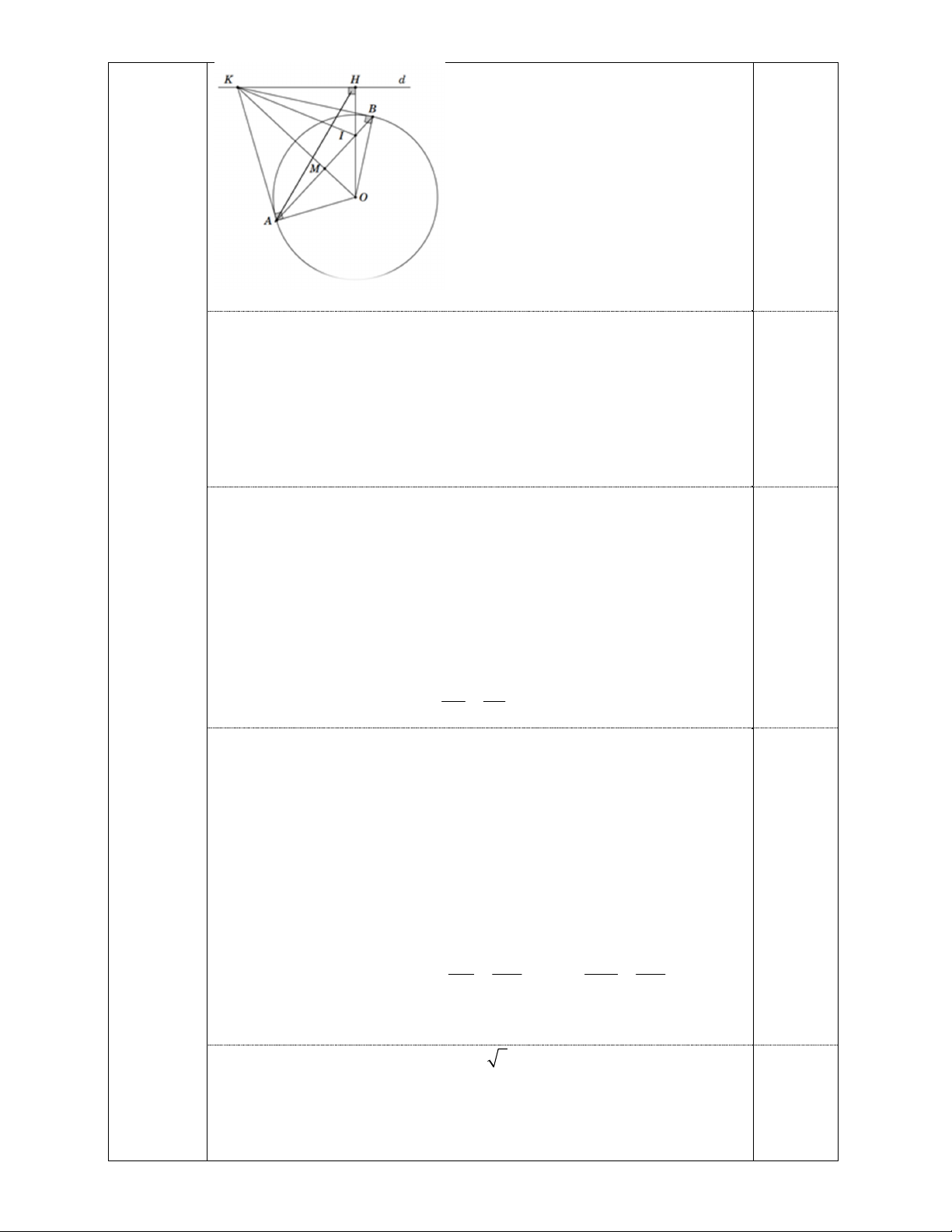
Bài 4:(3,5 điểm)Cho đường tròn tâm O , bán kính R và một đường thẳng d không cắt
đường tròn (O) . Dựng đường thẳng OH vuông góc với đường thẳng d tại điểm H . Trên
đường thẳng d lấy điểm K (khác điểm H ), qua K vẽ hai tiếp tuyến KA và KB với đường
tròn (O) , ( A và B là các tiếp điểm) sao cho A và H nằm về hai phía của đường thẳng OK
a) Chứng minh tứ giác KAOH là tứ giác nội tiếp.
b) Đường thẳng AB cắt đường thẳng OH tại điểm I . Chứng minh rằng IA IB  IH  IO
c) Chứng minh I là điểm cố định khi điểm K chạy trên đường thẳng d cố định.
d) Khi OK  2R,
OH  R 3 . Tính diện tích tam giác KAI theo R . x  2021 x  2022
Bài 5: (0,5 điểm)Tìm giá trị lớn nhất của A =  . x  1 x  1
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐Hết-‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐ UBND HUYỆN LONG ĐIỀN
ĐÁP ÁN ĐỀ THI THỬ TS LỚP 10 NH 2022 – 2023
TRƯỜNG THCS NGUYỄN THỊ ĐỊNH MÔN: TOÁN
( Thời gian làm bài 120 phút ) Câu Nội dung Điểm 1 a) (0.75 điểm) (3.5điểm) 2
x  3x  2  0
Lập:   1 (hoặc: a  b  c  0 ) 0.25
Phương trình có hai nghiệm: x  1; x  2 1 2 0.25x2 b) (0,75 điểm) 17 ìï y = 51 ì ï2x -3y = 5 - 6 ìï x-9y = 1 - 5 ï ï ï ï í  í  í 3y -5 0.25 ï3x + 4y = 18 6 ï x +8y = 36 ï î î x = ï ï ïïî 2 ì ïy = 3 ï ìïx = 2 ï ï 0.25x2  í 3.3-5 í . ïïx = ïy = 3 2 ïî ïî
Vậy hệ phương trình có nghiệm duy nhất: (x; y) = (2; 3).
(Nếu học sinh chỉ ghi kết quả đúng thì chỉ được 0.25 điểm) c) (1điểm)     2 6 A 2 3  75 2  3 62  3 =  2  3  5 3 0.25x2 4  3
12  6 3  2  3  5 3 14 0.25x2 d) (1 điểm) 2
x  5  x  10x  2x 1 ĐKXĐ: 0  x  5     2   2 x 5 x 10x  2x 12 0.25 
x  2 x(5  x)  5  x  2x(5  x) 1
 2x(5  x)  2 x(5  x)  4  0
 x(5  x)  x(5  x)  2  0 (1) 0.25
Đặt t  x(5  x) ( t  0) 2  t  x(x  5)
(1)  t2 – t – 2 = 0 (*)
Ta có: a - b + c = 1 – (-1) + (-2) = 0
Nên pt (*) có 2 nghiệm là t1 = -1 ( loại);  t 2 = c  2 ( nhận) a
Với t = 2, ta có: 22 = x(5 - x)  x2 – 5x + 4 = 0 (**) 0.25
Ta có: a + b + c = 1 + (-5) + 4 = 0
Nên pt (**) có hai nghiệm x1 = 1 ( nhận); x2= c  4 ( nhận) a
Vậy pt(1) có hai nghiệm là 1; 4. 0.25
Lưu ý: Hs làm cách khác cho kết quả đúng thì trọn điểm 2 a) (1.0điểm) (2.0điểm) * y= x2 Bảng giá trị x -3 -2 -1 0 1 2 3 y = x2 9 4 1 0 1 4 9 0.25 * y = mx – m +2 Với m = 1 thì: y = x + 1
Cho x= 0 thì y = 1 ta được (0;1)
y = 0 thì x = -1 ta được (-1; 0) 0.25
Đồ thị: (cả hai đồ thị chính xác) 0.5
Hs vẽ đồ thị đúng mỗi đồ thị được 0,25 điểm, trục tọa độ thiếu 2
trong 3 tên O, x, y thì không cho điểm. b) (1.0điểm)
Phương trình hoành độ giao điểm của (P) và (d) là: 0.25 2 2
x  mx  m  2  x  mx  m  2  0
(d) cắt (p) tại hai điểm phân biệt 2
   0  (m  2)  4  0 0.25 (đúng m   R) ,
Vì x x là hai nghiệm của phương trình hoành độ giao điểm nên 1 2
x  x  m 1 2
theo hệ thức Vi-et ta có:  0.25
x .x  m  2  1 2 2
Khi đó : x  x  1  (x  x )  1 1 2 1 2 2 
(x  x )  4x x  1 1 2 1 2 2 2
 m  4(m  2)  1  m  4m  7  0 0.25
Phương trình này vô nghiệm. Vậy không tìm được giá trị nào của m
thõa mãn điều kiện đề bài. 3 (0,5 điểm) ABC  vuông tại B, có: BC BC 3000 SinA   AC    6000 m 0 AC SinA Sin30 0.25
vận tốc trung bình của máy bay trong trường hợp này là: 6000 0.25  200 m/s 30 4 Hình
vẽ (Vẽ hình chỉ để c/m câu a thì được 0.25 đ) 0.5 (3.5 điểm)
a) (1 điểm) Chứng minh tứ giác KAOH là tứ giác nội tiếp. Tứ giác KAOH có:  KAO 90  (KA là tiếp tuyến) 0.25  0.25 KHO 90  (OH  KH ) 0.25   KAO KBO 180    Mà hai góc này đối nhau
Nên tứ giác KAOH nội tiếp đường tròn đường kính OK 0.25
b)(0,75 điểm) Chứng minh rằng IA IB  IH  IO
Tứ giác KAOH nội tiếp đường tròn đường kính OK (cmt) Mà KB 
O vuông tại B (KB là tiếp tuyến)  K , B,O thuộc đường tròn đường kính OK Vậy năm điểm K, ,
A B,O, H cùng thuộc đường tròn đường kính OK 0.25
Xét  IAH và  IOB có:  
HIA  BIO (đối đỉnh)  
AHI  ABO (hai góc nội tiếp cùng chắn cung AO ). Do đó IA IO
IAH ∽ IOB (g.g)  
 IA IB  IH  IO . 0.25x2 IH IB
c) (0,75 điểm) Chứng minh I là điểm cố định khi điểm K chạy
trên đường thẳng d cố định
Xét tứ giác AOBH nội tiếp có: 
OHB là góc nội tiếp chắn cung OB 
OBA là góc nội tiếp chắn cung OA
Mà OA  OB  R nên   OHB  OBA . 0.25 Xét OI  B và OB  H có :  BOH góc chung  
OHB  OBA (cmt). 2 2 OI OB OB R 0.25
Do đó OIB ∽ OBH (g.g)    OI   . OB OH OH OH
Ta lại có đường thẳng d cố định nên OH không đổi ( OH  d ).
Vậy điểm I cố định khi K chạy trên đường thẳng d cố định 0.25
d) (0,5 điểm) Khi OK  2R,
OH  R 3 . Tính diện tích tam giác
KAI theo R
Gọi M là giao điểm của OK và AB
Theo tính chất hai tiếp tuyến cắt nhau ta có KA=KB;
Lại có OA  OB  R nên OK là đường trung trực của AB, suy ra
AB  OK tại M và MA  MB . 2 2 R R R
Theo câu b) ta có OI    . OH R 3 3 Xét OAK  vuông tại A , có 2 2 2 OA R R
OA  OM OK  OM    OK 2R 2 Suy ra R 3R
KM  OK  OM  2R   2 2 0.25 2 2 R 3R 3R R 3
AM  OM  KM     AM  2 2 4 2 Xét OMI  vuông tại M , có 2 2  R   R  R 3 2 2
MI  OI  OM         3   2  6 Suy ra R 3 R 3 2R 3
AI  AM  MI    2 6 3 2 0.25 Diện tích  1 1 3R 2R 3 R 3
AKI là S  AI  KM     . 2 2 2 3 2 5 x  2021 x  2022
(0,5 điểm) Tìm giá trị lớn nhất của A =  . x  1 x  1
Đặt a  x  2021 ; b  x  2022 ( a, b  0) 2
a  2022  x 1   2
b  2021  x 1 a b Ta có: A =  0.25 2 2
a  2022 b  2021  a  b 1 1   2a 2022 2b 2021 2 2022 2 2021 1 1 2 a  2022 A   khi max  2 2022 2 2021 2 b  2021 x  2021  2022    x  4043 x  2022  2021 1 1 0.25 Vậy GTLN của A là  khi x = 4043 2 2022 2 2021