Đề thi thử Toán vào lớp 10 năm 2022 vòng 5 trường THCS Nguyễn Công Trứ – Hà Nội

UBND QUẬN BA ĐÌNH
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
TRƯỜNG THCS NGUYỄN CÔNG TRỨ NĂM HỌC 2021 - 2022 VÒNG 5 Môn thi: TOÁN
Ngày thi: 11 tháng 6 năm 2022
Thời gian làm bài: 120 phút.
Bài I (2,0 điểm)
Cho hai biểu thức: A = √x+3 và B = √x + 4x (với x > 0; 𝑥 ≠ 4) √x−2 √x−2 2√x−x
a) Tính giá trị của biểu thức A khi x = 16 b) Rút gọn P = " #
c) Tìm giá trị nguyên lớn nhất của x để P > −2
Bài II (2,5 điểm)
1. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Bạn Dương đi xe đạp từ tỉnh A đến tỉnh B dài 45km. Khi từ tỉnh B quay trở về tỉnh
A, Dương đi theo đường khác dài hơn 9km. Vì lúc về vận tốc của Dương tăng hơn so với
lúc đi là 3km/h nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của Dương
lúc đi từ tỉnh A đến tỉnh B?
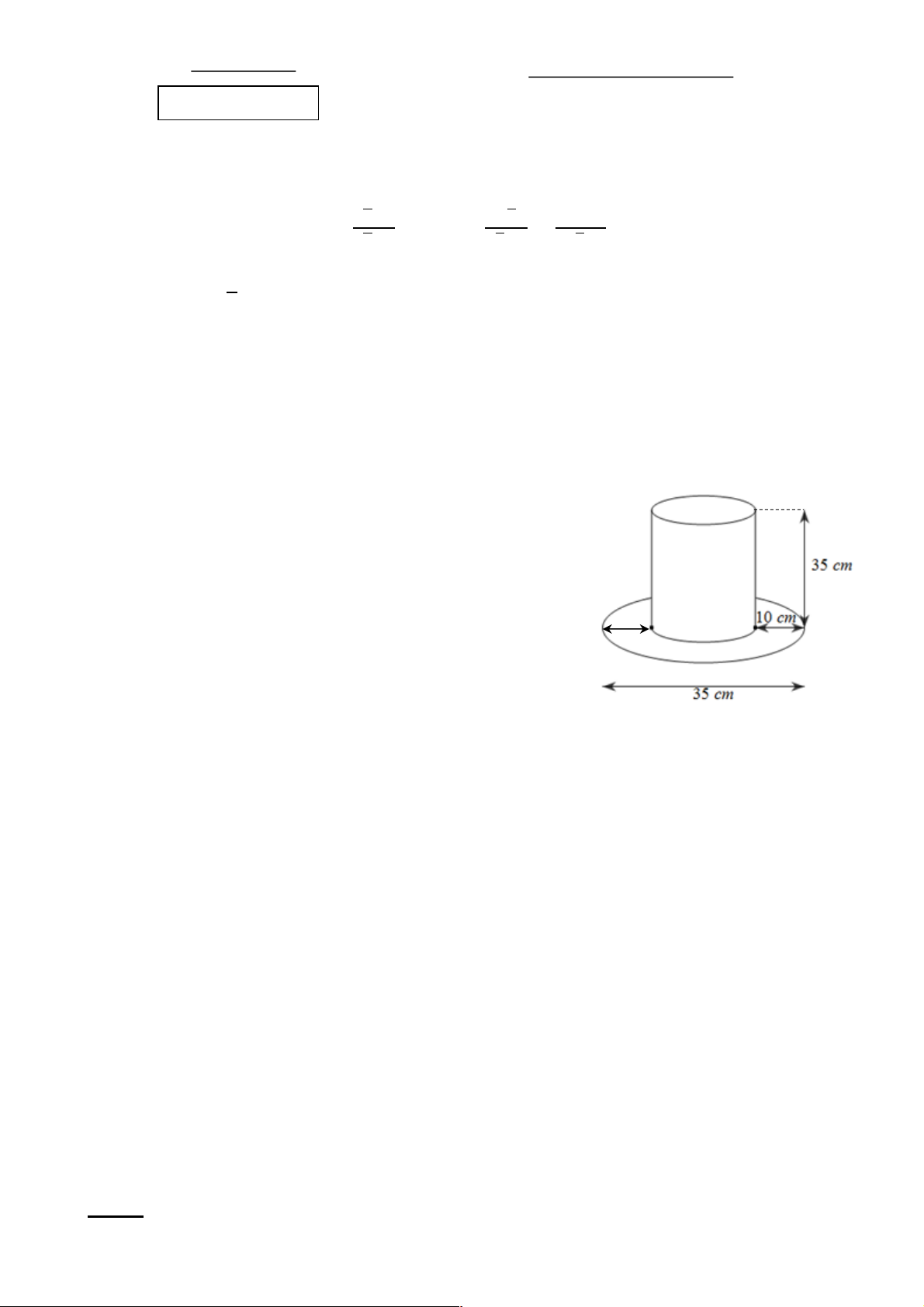
2. Một chiếc mũ của nhà ảo thuật với các kích
thước cho ở hình bên. Tính diện tích vải cần có để
làm nên chiếc mũ (không kể riềm, mép, phần thừa). (Lấy p» 3,14) 10cm
Bài III (2,0 điểm) 2|𝑥 − 1| − 5𝑦 = 3
1. Giải hệ phương trình: 1 5|𝑥 − 1| + 10𝑦 = −3
2. Trong mặt phẳng tọa độ Oxy cho
Parabol (P): 𝑦 = x$ và đường thẳng (d): y = 2(m − 1)x − m + 3
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt A và B.
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành. Tìm m để H và K đối xứng nhau qua O.
Bài IV(3,0 điểm)
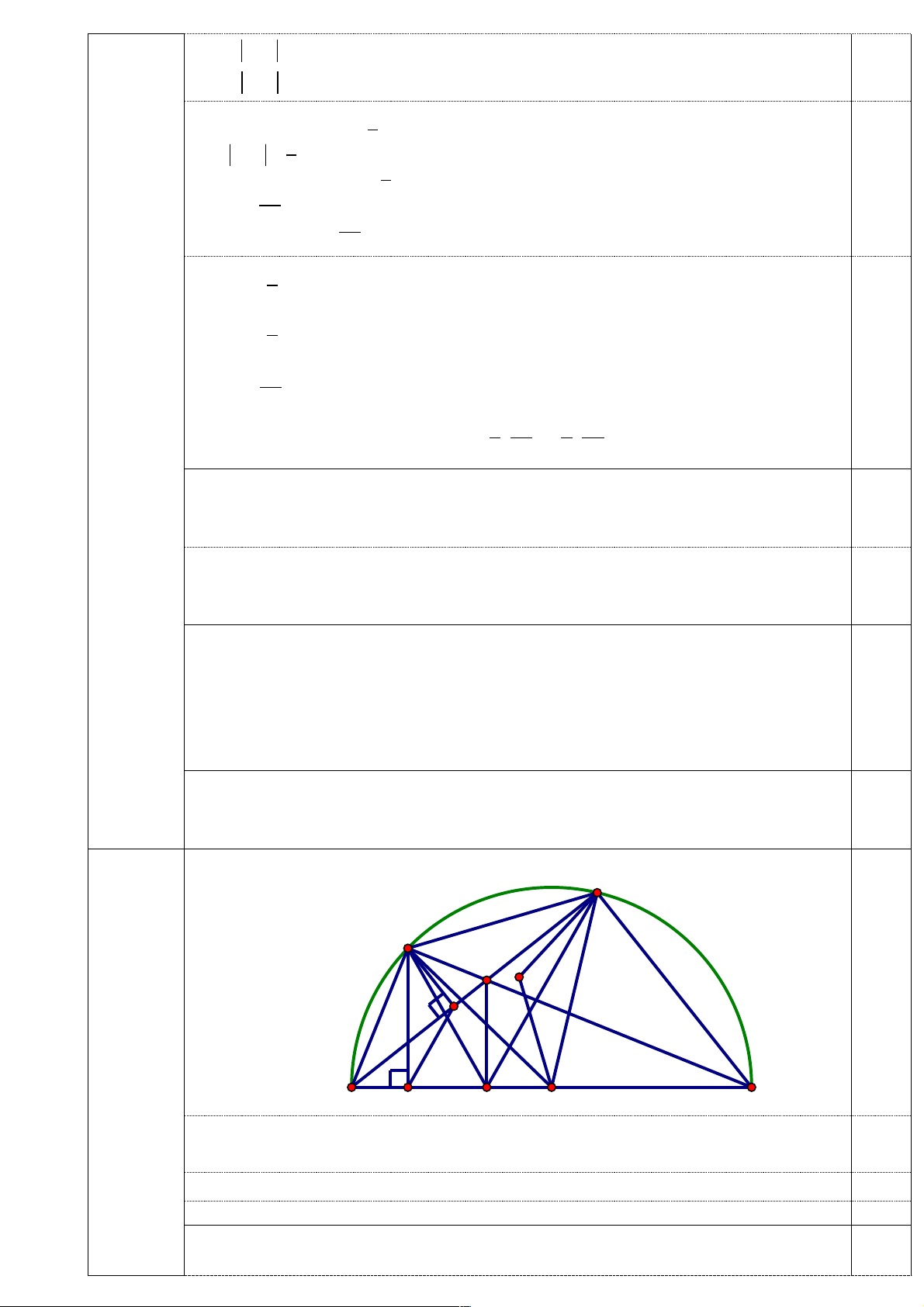
Cho nửa đường tròn tâm (O), đường kính AB = 2R và điểm C cố định trên nửa
đường tròn sao cho AC > BC. Điểm M di động trên cung AC (M ≠ A; M ≠ C). Kẻ MH
vuông góc AB tại H; kẻ MI vuông góc AC tại I.
a) Chứng minh: tứ giác AMIH nội tiếp được.
b) Chứng minh: ∆MIH đồng dạng với ∆MCB, từ đó tìm vị trí của điểm M để CB = 2IH.
c) Gọi K là giao điểm của AC và BM. Kẻ KE vuông góc AB tại E. Chứng minh tâm
đường tròn ngoại tiếp ∆MCE chạy trên một đường thẳng cố định.
Bài V (0,5 điểm)
Giải phương trình: 4𝑥% − 7𝑥& + 9𝑥$ − 10𝑥 + 4 = 0
---------------------------HẾT---------------------------
Lưu ý: Cán bộ coi thi không giải thích gì thêm!
Họ và tên:………… …………………………………SBD:……………………...
Giám thị 1:…………………………. ; Giám thị 2:………………………………. UBND QUẬN BA ĐÌNH
HƯỚNG DẪN CHẤM ĐỀ KSCL HỌC SINH LỚP 9 TRƯỜNG THCS
NĂM HỌC 2021 – 2022
NGUYỄN CÔNG TRỨ Môn thi: TOÁN
Ngày thi: 11 tháng 5 năm 2022 VÒNG 5 Bài Đáp án Điểm
a) Thay x = 16 (TMĐK) vào A 0,25 16 + 3 7 A = = 16 - 2 2 0,25 B æ x 4x ö x + 3 b) P = Þ P = ç + ÷ : A ç x 2 2 x x ÷ - - x - 2 è ø 0,25 æ ö x 4x x - 2 P ç ÷ = - . ç x - 2 x è ( x -2)÷ x +3 ø 0,25 Bài I (2 điểm) 3 - x x - 2 P = . 0,25 x - 2 x + 3 3 - x P = x + 3 0,25 c) P > 2 - 3 - x - x + 6 Û > 2 - Û > 0 x + 3 x + 3 0,25
có x + 3 > 0 Þ - x + 6 > 0
Þ x < 36 mà x là số nguyên lớn nhất Þ x = 35 (TMĐK) 0,25
1) Gọi vận tốc lúc đi từ A đến B là x (km/h, x >0) 0,25 45
Thời gian đi từ A đến B là : (giờ) x 0,25
Quãng đường từ B về A là : 45 + 9 = 54 (km)
Vân tốc đi từ B về A là : x + 3 (km/h) 0,25 54
Thời gian đi từ B về A là (giờ) x + 3 0,25 1
Thời gian về ít hơn thời gian đi là 30 phút =
giờ nên ta có phương trình : 2 45 54 1 Bài II - = (2,5 điểm) x x + 3 2 0,25 Û …… 2
Û x + 21x - 270 = 0 éx = 9(TM ) Û ê ëx = 30( - KTM ) 0,5
Vậy bạn Dương đi từ A đến B với vận tốc là 9km/h 0,25
2)Bán kính thân mũ là: (35 – 10.2 ): 2 = 15 cm = 7,5cm
Diện tích thân mũ là: Sxq + S đáy = dph + r2p = 15.p .35 + 7,52p = 581,25p cm2 Diện tích vành mũ là: 2 2
(35: 2) p - (15: 2) p = 250p cm2 0,25
Diện tích vải để làm mũ là: p+ p = p( 2) » ( 2 581,25 250 831,25 cm 2610,25 cm ) Kết luận 0,25
1) Giải hệ phương trình :
ì2 x -1 - 5y = 3
ì4 x -1 -10y = 6 ï ï í Û í 5 ï x -1 +10y = 3 - 5 î ï x -1 +10y = 3 - î 0,25 9 ì x -1 = 3 ï Û í
ï2 x -1 - 5y = 3 î 0,25 ìé 1 x -1 = ïê ì 1 3 x -1 = ïê ï ï 3 ï 1 ê Û í í x -1 = - 7 - êë 3 ïy ï = ïî 15 ï 7 - ïy = î 15 0,25 ìé 4 x = ïê 3 ïê ï 2 ê Û í x = êë 3 ï ï -7 ï y = î 15 æ 4 -7 ö æ 2 7 - ö
Kết luận: Hệ phương trình có nghiệm ; ; ; ç ÷ ç ÷ è 3 15 ø è 3 15 ø 0,25 Bài III
2)a) Xét phương trình hoành độ giao điểm của (P) và (d) : (2,0 điểm) 2 2
x = 2(m -1)x - m + 3 Û x - 2(m -1)x + m - 3 = 0 (1) 2 2 2
D = [ - 2(m -1)] - 4.1.(m -3) = 4m -8m + 4 - 4m +12 = 4m -12m +16 0,25 2
= (2m -3) + 7 > 0với mọi giá trị của m
=> pt (1) luôn có hai nghiệm phân biệt với mọi giá trị của m
=> (d) luôn cắt (P) tại hai điểm phân biệt A và B với mọi giá trị của m 0,25
b) Gọi x ; x là hoành độ của A và B => x ; x là hai nghiệm của pt (1) 1 2 1 2
ìx + x = 2m - 2
Theo hệ thức vi-et ta có : 1 2 í
x .x = m - 3 î 1 2
H, K là hình chiếu của A và B trên trục hoành Þ H(x ;0), K(x ;0) 1 2
H và K đối xứng nhau qua O => x + x = 0và x .x < 0 1 2 1 2 0,25 ì2m - 2 = 0 ìm =1 => í Û í Û m = 1 îm - 3 < 0 îm < 3 Vậy m =1 0,25 Vẽ hình đến câu a C M K D I Bài IV (3 điểm) A H E B O 0,25
a) MH ꓕ AB tại H (gt) Þ ∑ 0 MHA = 90 MI ꓕ AC tại I (gt) Þ ∑ 0 MIA = 90 0,25 Tứ giác AMIH có ∑ ∑ 0
MHA = MIA = 90 mà H và I là hai đình kề nhau 0,25
Þ Tứ giác AMHI nội tiếp (dhnb) 0,25
b) Tứ giác AMIH nội tiếp (cmt) Þ ∑ ∑
MAI = MHI ( Hai góc nội tiếp cùng chắn cung MI) 0,25 ∑ ∑
IMH = IAH ( Hai góc nội tiếp cùng chắn cung HI)
Xét đường tròn (O), ta có : ∑ ∑
MAI = MBC ( Hai góc nội tiếp cùng chắn cung MC) ∑ ∑
CMB = IAH (Hai góc nội tiếp cùng chắn cung BC) 0,25 Suy ra ∑ ∑ ∑ ∑
MHI = MBC; IMH = CMB Þ MI
D H đồng dạng với M
D CB(g - g) 0,25 Þ MI IH = (t / c) MC CB CB =2IHÞMC = 2MI MI ΔMIC vuông tại I Þ ∑ sin MCI = Þ ∑ 1 sin MCI = Þ ∑ 0 MCI = 30 MC 2
Xét đường tròn (O), ta có ∑ 1 MCA = sđ !
AM (góc nội tiếp)Þsđ ! 0 AM = 60 2 ∑ AOM =sđ !
AM (đl góc ở tâm)Þ ∑ 0 AOM = 60 0,25
Có ΔAOM cân tại O (OA =OM =R) mà ∑ 0
AOM = 60 Þ ΔAOM đều ÞAM = R
Vậy M trên cung AC sao cho AM = R thì CB = 2IH 0,25
c) Chứng minh tứ giác AMKE nội tiếp Þ ∑ ∑ MAK = MEK
Chứng minh tứ giác BCKE nội tiếp Þ ∑ ∑ CBK = CEK 0,25 Þ ∑ ∑ ∑ ∑ ∑
MEC = MEK + CEK = MAC + MBC Þ ∑ 1 1 MEC = sđ ! MC + sđ ! MC =sđ ! MC 2 2 Xét (O) có ∑ MOC =sđ ! MC (đl góc ở tâm) Þ ∑ ∑
MEC = MOC ÞTứ giác MEOC nội tiếp 0,25
Gọi D là tâm của đường tròn ngoại tiếp tam giác MCE Þ D là tâm của đường tròn ngoại
tiếp tứ giác MEOCÞ DO = DC Þ D thuộc trung trực của OC
Do O,C cố định Þ OC cố định Þ đường Trung trực của OC cố định
Vậy khi M chạy trên cung AC thì tâm đường trong ngoại tiếp tam giác MCE chạy trên
đường thẳng cố định là trung trực của OC 0,25 4 3 2
4x - 7x + 9x -10x + 4 = 0 3 2
Û 4x (x -1) - 3x (x -1) + 6x(x -1) - 4(x -1) = 0 3 2
Û (x -1)(4x - 3x + 6x - 4) = 0 éx = 1 (1) Û ê 3 2 Bài V
ë4x - 3x + 6x - 4 = 0 (2) 0,25 (0,5 điểm) Giải (2) 3 2 3 2 3 3 2
4x - 3x + 6x - 4 = 0 Û 8x - 6x +12x - 8 = 0 Û 7x + x - 6x +12x - 8 = 0 2 3 3 3 Û (x - 2) = 7
- x Û x - 2 = - 7x Û x = 3 1+ 7 ì 2 ü
Vậy phương trình có nghiệm x Î 1 í ; ý 3 î 1+ 7 þ 0,25
Lưu ý:-Điểm toàn bài để lẻ đến 0,25.
- Các cách làm khác nếu đúng vẫn cho điểm tối đa.