Đề thi thử Toán vào lớp 10 năm 2023 – 2024 lần 3 phòng GD&ĐT Lộc Hà – Hà Tĩnh

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ VÀO LỚP 10 THPT HUYỆN LỘC HÀ
NĂM HỌC 2023 – 2024 (Lần 3)
ĐỀ THI CHÍ NH THỨC Mã Đề 01 Môn thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
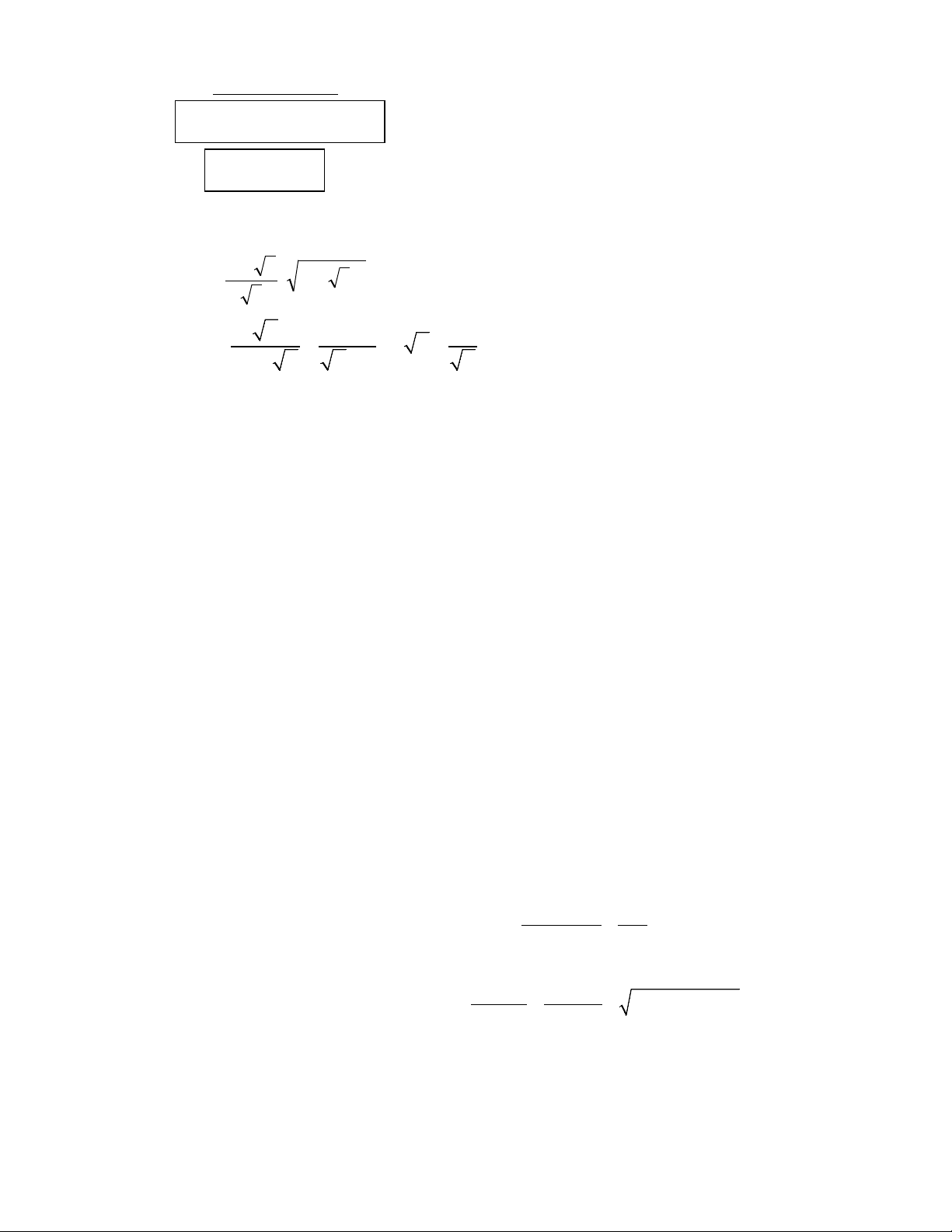
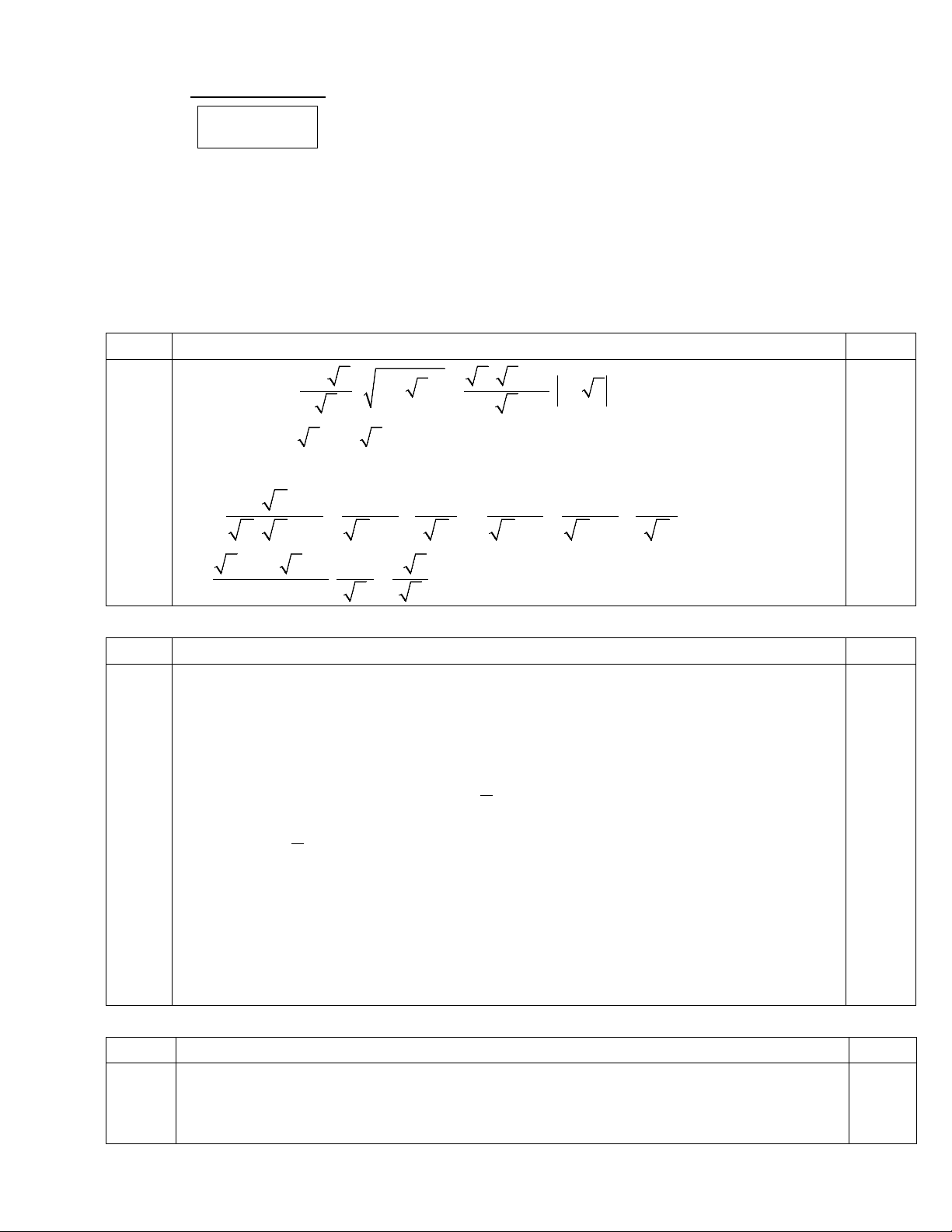
Câu 1. Rút gọn các biểu thức  +  a) P =     ( − )2 2 2 1 2 .  2    b) x 1  9 Q  . x  = + −
với x > 0 , x ≠ 9 .  x 3 x x 3  x  − +  
Câu 2. a) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d):y= xm+2m+3 và đường thẳng (d ): 1 y = 2
− x+1. Tìm m để hai đường thẳng (d) và ( d ) cắt nhau tại điểm M có hoành độ bằng 2. 1
b) Giải hệ phương trình x − 2y = 3 −  . 2x + 3y = 8
Câu 3. Cho phương trình 2 2
x − 2mx + m + 2m − 3 = 0 (m là tham số). Tìm m để phương trình có hai
nghiệm phân biệt x , x thỏa mãn 2 2
x + x − x x = 4 . 1 2 1 2 1 2
Câu 4. Bác Hà đến một cửa hàng để mua một nồi cơm điện nhãn hiệu Cuckoo và một chiếc quạt
nhãn hiệu Senko. Theo giá niêm yết thì bác Hà phải thanh toán cho hai món đồ trên với tổng số
tiền 4000000 đồng. Nhưng khi thanh toán thì cửa hàng giảm giá 10% cho nồi cơm điện và 8% cho
quạt điện nên bác Hà chỉ phải thanh toán 3630000 đồng. Hỏi giá niêm yết trên mỗi sản phẩm mà
bác Hà đã mua là bao nhiêu?
Câu 5. Cho tam giác ABC vuông tại A, đường cao AH (H∈BC). Biết AH = 3 cm ,  = 0 ACB 30 . Tính AC và AB.
Câu 6. Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC
với đường tròn (O) (B và C là các tiếp điểm). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai
là D; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E; đường thẳng BE cắt AO tại F; H là giao điểm của AO và BC.
a) Chứng minh tứ giác ABOC nội tiếp. 2
b) Chứng minh Tứ giác ODEH nội tiếp và HB DE − = 1. 2 2 AF − EF AE
Câu 7. Cho a, b là các số thực dương thoả mãn a + b = ab .
Tìm giá trị nhỏ nhất của biểu thức 1 1 2 2 P = +
+ (1+ a )(1+ b ) . 2 2
a + 2a b + 2b
.………….. Hết……………
Ghi chú: - Thí sinh không được sử dụng tài liệu.
- Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh..............................................SBD......................... 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ VÀO LỚP 10 THPT HUYỆN LỘC HÀ
NĂM HỌC 2023 - 2024 (Lần 3) ĐỀ THI C HÍNH THỨC Mã Đề 02 Môn thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Câu 1. Rút gọn các biểu thức  +  a) 3 3 P = (1− )2 3  .  3    b) x 1  4 Q  . x  = + −
với x > 0 , x ≠ 4.  x 2 x x 2  x  − +  
Câu 2. a) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d):y= x -
m 2m +1 và đường thẳng ( d ): 1 y = 2
− x-1. Tìm m để hai đường thẳng (d) và ( d ) cắt nhau tại điểm M có hoành độ bằng -2. 1
b) Giải hệ phương trình 3x + y = −4  .
2x − 3y = −10
Câu 3. Cho phương trình 2 x − 2 2
mx + m − 2m + 3 = 0 (m là tham số). Tìm m để phương trình có hai
nghiệm phân biệt x , x thỏa mãn 2 2
x + x − x x = . 1 2 1 2 7 1 2
Câu 4. Bác Hà đến một cửa hàng để mua một nồi cơm điện nhãn hiệu Cuckoo và một chiếc quạt
nhãn hiệu Senko. Theo giá niêm yết thì bác Hà phải thanh toán cho hai món đồ trên với tổng số
tiền 4000000 đồng. Nhưng khi thanh toán thì cửa hàng giảm giá 8% cho nồi cơm điện và 10% cho
quạt điện nên bác Hà chỉ phải thanh toán 3650000 đồng. Hỏi giá niêm yết trên mỗi sản phẩm mà
bác Hà đã mua là bao nhiêu?
Câu 5. Cho tam giác ABC vuông tại A, đường cao AH (H∈BC). Biết AH = 2 cm ,  = 0 ACB 30 . Tính AC và AB.
Câu 6. Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC
với đường tròn (O) (B và C là các tiếp điểm). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai
là D; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E; đường thẳng BE cắt AO tại F; H là giao điểm của AO và BC.
a) Chứng minh tứ giác ABOC nội tiếp. 2
b) Chứng minh Tứ giác ODEH nội tiếp và HB DE − = 1. 2 2 AF − EF AE
Câu 7. Cho x, y là các số thực dương thoả mãn x + y = xy .
Tìm giá trị nhỏ nhất của biểu thức 1 1 2 2 P = +
+ (1+ x )(1+ y ) . 2 2
x + 2x y + 2y
.………….. Hết……………
Ghi chú: - Thí sinh không được sử dụng tài liệu.
- Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh..............................................SBD......................... 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM ĐỀ THI THỦ VÀO HUYỆN LỘC HÀ
LỚP 10 THPT MÔN TOÁN Năm học 2023 - 2024 Mã Đề 01 (Lần 3)
A. Một số chú ý khi chấm bài.
- Hướng dẫn dưới đây là lời giải sơ lược của một cách. Học sinh có cách giải khác mà
cho kết quả đúng thì vẫn cho điểm tối đa.
- Giáo viên cần bám sát phần lí luận và tính toán của học sinh để cho điểm.
B. Đáp án và biểu điểm. Câu 1: (2,0đ) Câu H­íng dÉn §iÓm a) Ta có  +  P =   0.5   ( − )2 2 2 2( 2 +1) 1 2 = .1− 2 1  2  2
= ( 2 + )1( 2 − )1 = 2−1=1 0.5 b) Ta có  x 1  x − 9  1 1  x − 9 Q =  + . = + 0.5  .  x ( x − 3) x + 3 x  x −3 x + 3  x
x + 3+ x − 3 x − 9 2 0.5 = . x = = 2 . x − 9 x x Câu 2: (2,0đ) Câu H­íng dÉn §iÓm a)
2 + Tung độ của điểm M là y = 2.2 − +1= -3
Suy ra tọa độ giao điểm M(2; -3) 0.5
+ Đường thẳng (d): y = x
m +2m+3 đi qua điểm M(2; -3) nên ta có 3 3 − = .
m 2+2m+3 ⇔ 4m = 6
− ⇔ m = − (thỏa mãn yêu cầu bài toán). 2 0.5 Vậy 3 m = − . 2 x − 2y = 3 − 2x − 4y = 6 − b)  ⇔ 0.5 2x 3y 8  + = 2x + 3y = 8 7y =14 x =1 ⇔  ⇔ x 2y 3  − = − y = 2 0.5
Vậy hệ phương trình đã cho có nghiệm (x; y) = (1; 2). Câu 3: (1,0đ) Câu H­íng dÉn §iÓm 2 2
x − 2mx + m + 2m − 3 = 0 (1) 3 Ta có '∆ = 2 − m + 3
Phương trình (1) có 2 nghiệm phân biệt x , x khi 1 2 1 ' 3 ∆ > 0 ⇔ 2
− m + 3 > 0 ⇔ m < (*) 0.25 2
Theo hệ thức Vi-ét, ta có x + x = 2m 0.25 1 2  2
x .x = m + 2m −  3 1 2 Khi đó 2 2 2 0.25
x + x − x x = 4 ⇔ (x + x ) − 3x x = 4 1 2 1 2 1 2 1 2 m =1 2 2 2
⇒ 4m − 3(m + 2m − 3) = 4 ⇔ m − 6m + 5 = 0 ⇔  0.25 m = 5
Đối chiếu với ĐK (*), ta có m =1 là giá trị cần tìm. Câu 4: (1,0đ) Câu H­íng dÉn §iÓm
Gọi giá niêm yết của một chiếc nồi cơm điện là x (đồng) ( x > 0 )
4 Giá niêm yết của một chiếc quạt điện là y (đồng) ( y > 0)
Theo bài ra ta có phương trình x + y = 4000000 (1) 0.25
Sau khi giảm giá, bác Hà phải trả tổng số tiền khi mua nồi cơm điện và
quạt điện trên là 3630000 đồng, ta có phương trình 0,9x + 0,92y = 3630000(2) 0.25
Từ (1) và (2) ta có hệ phương trình:
x + y = 4000000  0.25
0,9x + 0,92y = 3630000
Giải hệ phương trình ta đượcx = 2500000  (thỏa mãn). 0.25 y = 1500000
Vậy giá niêm yết của một chiếc nồi cơm điện và quạt điện lần lượt là
2500000 đồng và 1500000 đồng. Câu 5: (1,0đ) Câu Hướng dẫn Điểm
Có vẽ hình (mới chấm điểm) 5 Ta có: AH 3 AC = = = 6cm 0 Sin 0.5 C Sin 30
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có 1 1 1 1 1 1 1 1 1 = + ⇒ = − = − = ⇒ AB = 2 3 (cm). 2 2 2 2 2 2 2 2 AH AB AC AB AH AC 3 6 12 0.5 Câu 6: (2,0đ) Câu H­íng dÉn §iÓm
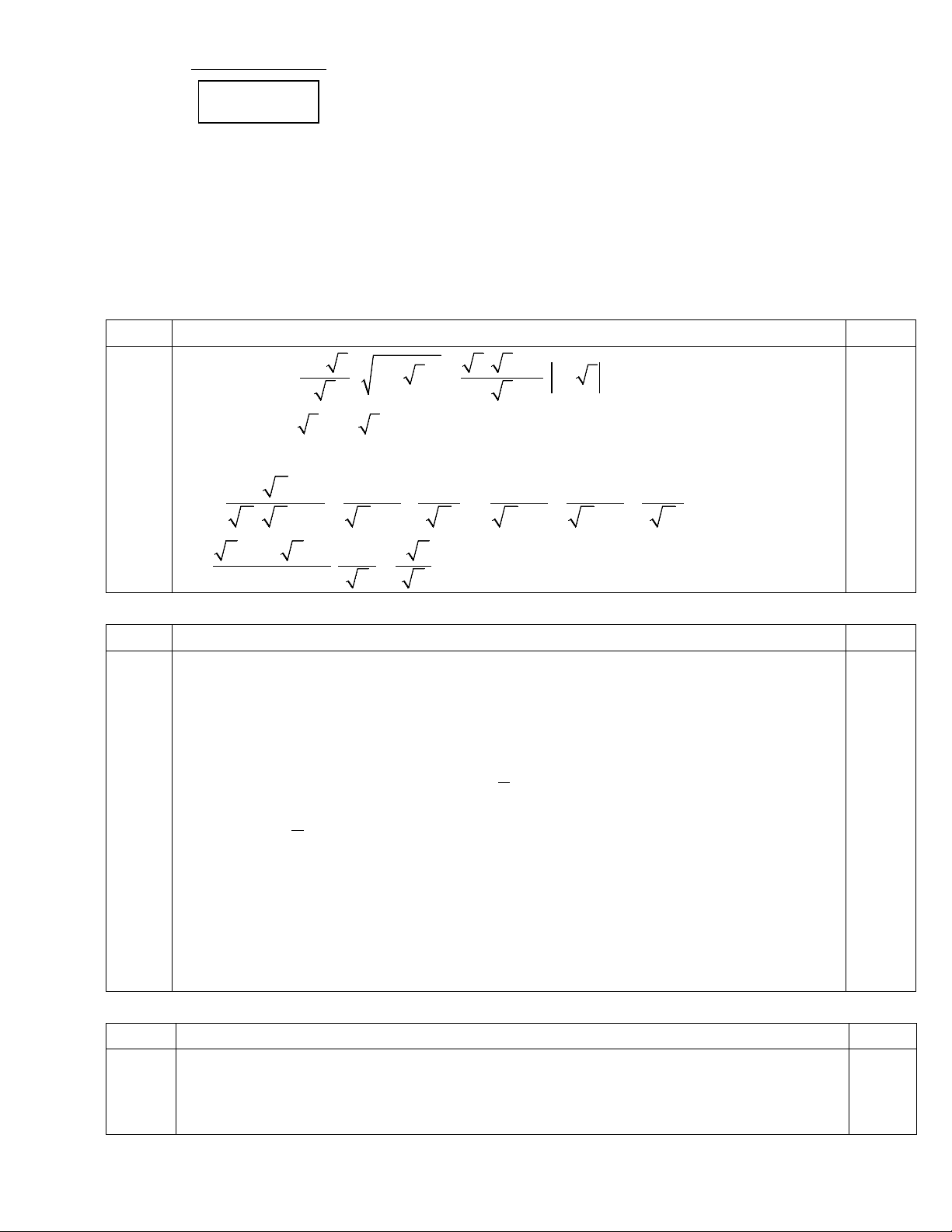
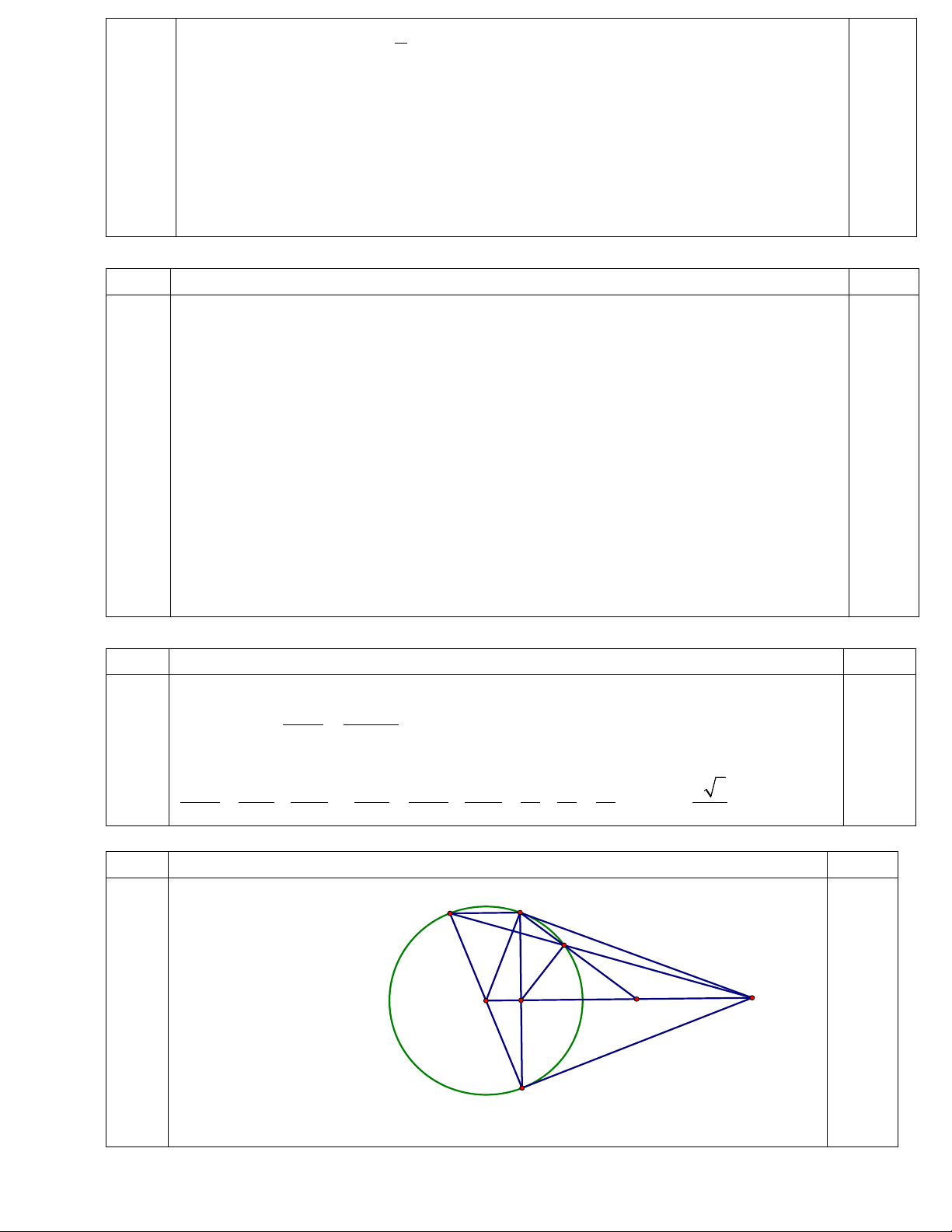
a) Có vẽ hình (chính xác) D B 6 E 0.25 O A H F C 1 Ta có: ⊥ ⇒  = 90 .o OB AB OBA
( tính chất tiếp tuyến). (1) ⊥ ⇒  = 90 .o OC AC OCA
( tính chất tiếp tuyến). (2) 0.75
Từ (1) và (2) suy ra  +  0
OBA OCA =180 . Vậy tứ giác ABOC nội tiếp. b) Chứng minh được A
∆ HE đồng dạng A ∆ DO ( c.g.c) ⇒  =  EHA ADO 0.25
Kết luận được tứ giác ODEH nội tiếp đường tròn
Tứ giác ODEH nội tiếp ⇒  =  DEH HOC 0.25 Chỉ ra  = 
BCD BED (Hai góc nội tiếp cùng chắn  BD của (O)) Mà  +  0
HOC OCH = 90 (Tam giác OHC vuông tại H) ⇒  +  0 HED BED = 90 ⇒  0
HEB = 90 ⇒ HE ⊥ BF tại E
Chứng minh HF2 = FE.FB, AF2 = FE.FB ⇒ HF2 = AF2 Chứng minh HB2 = BE.BF
⇒ AF2 – EF2 = HF2 – EF2 = HE2 = EB.EF 2 ⇒ HB BE.BF BF = = 2 2 AF − EF BE.EF EF 0.25 Chứng minh B
∆ DE đồng dạng F
∆ AE (g.g) ⇒ DE BE = AE EF 2 − ⇒ HB DE BF BE BF BE EF − = − = = =1 (đpcm). 0.25 2 2 AF − EF AE EF EF EF EF Câu 7: (1,0đ) Câu H­íng dÉn §iÓm 2 Ta có (a + b)
a + b = ab ≤ ⇒ a + b ≥ 4 7 4 2 2 2 2 2 2 2 2 2
(1+ a )(1+ b ) =1+ a + b + a b ≥1+ 2ab + a b = (1+ ab) 2 2
⇒ (1+ a )(1+ b ) ≥1+ ab =1+ a + b (1) 0.25
Áp dụng BĐT quen thuộc 1 1 4 + ≥ ( x ∀ > 0, y > 0) x y x + y Ta có 1 1 4 4 + ≥ = 2 2 2 2 2 2
a + 2a b + 2b a + 2a + b + 2b a + 2(a + b) + b 4 4 = = (2) 2 2 2
a + 2ab + b (a + b) 2 Từ (1) và (2) 4 4
a + b a + b 7(a + b) ⇒ P ≥ + a + b +1 = + + + +1 0.25 2 2 (a + b) (a + b) 16 16 8
Áp dụng BĐT Cô si ta được 4
a + b a + b 7.4 3 7 21 P ≥ 33 . . + +1 = + +1 = . 0.25 2 (a + b) 16 16 8 4 2 4 Vậy 21 P =
khi a = b = 2 . min 4 0.25 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ THI THỦ VÀO HUYỆN LỘC HÀ
LỚP 10 THPT MÔN TOÁN Năm học 2023 - 2024 Mã Đề 02 (Lần 3)
A. Một số chú ý khi chấm bài.
- Hướng dẫn dưới đây là lời giải sơ lược của một cách. Học sinh có cách giải khác mà
cho kết quả đúng thì vẫn cho điểm tối đa.
- Giáo viên cần bám sát phần lí luận và tính toán của học sinh để cho điểm.
B. Đáp án và biểu điểm.
Câu 1: (2,0đ) Câu H­íng dÉn §iÓm a) Ta có  +  P =     ( − )2 3 3 3( 3 +1) 1 3 = .1− 3 1 0.5  3  3
= ( 3 + )1( 3 − )1 = 3−1= 2 0.5 b) Ta có  x 1  x − 4  1 1  x − 4 Q =  + . = +  . 0.5  x ( x − 2) x + 2 x  x − 2 x + 2  x
x + 2 + x − 2 x − 4 2 = . x = = 2 . 0.5 x − 4 x x Câu 2: (2,0đ) Câu H­íng dÉn §iÓm a)
2 + Tung độ của điểm M là y = 2.( − 2) − −1= 3
Suy ra tọa độ giao điểm M(-2; 3) 0.5
+ Đường thẳng (d): y = x-
m 2m+1 đi qua điểm M(-2; 3) nên ta có 1 3 = .( m 2) − − 2m+1 ⇔ 4
− m = 2 ⇔ m = − (thỏa mãn yêu cầu bài toán). 2 0.5 Vậy 1 m = − . 2 b) 3  x + y = 4 − 9  x + 3y = 12 −  ⇔ 0.5 2x 3y 10  − = −
2x − 3y = 10 − 11  x = 22 − x = 2 − ⇔  ⇔ 3  x y 4  + = − y = 2 0.5
Vậy hệ phương trình đã cho có nghiệm (x; y) = (-2; 2). Câu 3: (1,0đ) Câu H­íng dÉn §iÓm 2 x − 2 2
mx + m − 2m + 3 = 0 (1)
3 Ta có '∆ = 2m−3
Phương trình (1) có 2 nghiệm phân biệt x , x khi 1 2 1 ' 3
∆ > 0 ⇔ 2m − 3 > 0 ⇔ m > (*) 2 0.25
Theo hệ thức Vi-ét, ta có x + x = 2m 1 2  0.25 2
x .x = m − 2m +  3 1 2 Khi đó 2 2 2
x + x − x x = 7 ⇔ (x + x ) − 3x x = 7 1 2 1 2 1 2 1 2 0.25 m = 2 2 2 2
⇒ 4m − 3(m − 2m + 3) = 7 ⇔ m + 6m −16 = 0 ⇔  m = 8 − 0.25
Đối chiếu với ĐK (*), ta có m = 2 là giá trị cần tìm. Câu 4: (1,0đ) Câu H­íng dÉn §iÓm
Gọi giá niêm yết của một chiếc nồi cơm điện là x (đồng) ( x > 0 )
4 Giá niêm yết của một chiếc quạt điện là y (đồng) ( y > 0)
Theo bài ra ta có phương trình x + y = 4000000 (1) 0.25
Sau khi giảm giá, bác Hà phải trả tổng số tiền khi mua nồi cơm điện và
quạt điện trên là 3650000 đồng, ta có phương trình 0,92x + 0,9y = 3650000(2) 0.25
Từ (1) và (2) ta có hệ phương trình:
x + y = 4000000 0.25 
0,92x + 0,9y = 3650000
Giải hệ phương trình ta đượcx = 2500000  (thỏa mãn). 0.25 y = 1500000
Vậy giá niêm yết của một chiếc nồi cơm điện và quạt điện lần lượt là
2500000 đồng và 1500000 đồng. Câu 5: (1,0đ) Câu Hướng dẫn Điểm
Có vẽ hình (mới chấm điểm) 5 Ta có: AH AC 2 = = = cm 4 SinC Sin300 0.5
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có 1 1 1 1 1 1 1 1 3 = + ⇒ = − = − = 4 3 ⇒ AB = (cm). 0.5 2 2 2 2 2 2 2 2 AH AB AC AB AH AC 2 4 16 3 Câu 6: (2,0đ) Câu H­íng dÉn §iÓm
a) Có vẽ hình (chính xác) D B 6 E 0.25 O A H F C 1 Ta có: ⊥ ⇒  = 90 .o OB AB OBA
( tính chất tiếp tuyến). (1) ⊥ ⇒  = 90 .o OC AC OCA
( tính chất tiếp tuyến). (2) Từ (1) và (2) suy ra  0.75 +  0
OBA OCA =180 . Vậy tứ giác ABOC nội tiếp. b) Chứng minh được A
∆ HE đồng dạng A ∆ DO ( c.g.c) ⇒  =  EHA ADO 0.25
Kết luận được tứ giác ODEH nội tiếp đường tròn Tứ giác ODEH nội tiếp ⇒  =  DEH HOC 0.25 Chỉ ra  = 
BCD BED (Hai góc nội tiếp cùng chắn  BD của (O)) Mà  +  0
HOC OCH = 90 (Tam giác OHC vuông tại H) ⇒  +  0 HED BED = 90 ⇒  0
HEB = 90 ⇒ HE ⊥ BF tại E
Chứng minh HF2 = FE.FB, AF2 = FE.FB ⇒ HF2 = AF2 Chứng minh HB2 = BE.BF
⇒ AF2 – EF2 = HF2 – EF2 = HE2 = EB.EF 2 ⇒ HB BE.BF BF = = 0.25 2 2 AF − EF BE.EF EF Chứng minh B
∆ DE đồng dạng F
∆ AE (g.g) ⇒ DE BE = AE EF 2 − ⇒ HB DE BF BE BF BE EF − = − = = =1 (đpcm). 0.25 2 2 AF − EF AE EF EF EF EF Câu 7: (1,0đ) Câu H­íng dÉn §iÓm 2 Ta có (x + y)
x + y = xy ≤ ⇒ x + y ≥ 4 7 4 2 2 2 2 2 2 2 2 2
(1+ x )(1+ y ) =1+ x + y + x y ≥1+ 2xy + x y = (1+ xy) 2 2
⇒ (1+ x )(1+ y ) ≥1+ xy =1+ x + y (1) 0.25
Áp dụng BĐT quen thuộc 1 1 4 + ≥ ( a ∀ > 0,b > 0 ) a b a + b Ta có 1 1 4 4 + ≥ = 2 2 2 2 2 2
x + 2x y + 2y x + 2x + y + 2y x + 2(x + y) + y 4 4 = = (2) 2 2 2
x + 2xy + y (x + y) 2 Từ (1) và (2) 4 4
x + y x + y 7(x + y) ⇒ P ≥ + x + y +1 = + + + +1 0.25 2 2 (x + y) (x + y) 16 16 8
Áp dụng BĐT Cô si ta được 4
x + y x + y 7.4 3 7 21 P ≥ 33 . . + +1 = + +1 = . 2 0.25 (x + y) 16 16 8 4 2 4 Vậy 21 P =
khi x = y = 2 . min 4 0.25 1
Document Outline

• PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
• HUYỆN LỘC HÀ
• PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
• HUYỆN LỘC HÀ
• PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
• HUYỆN LỘC HÀ
• PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
• HUYỆN LỘC HÀ