

Preview text:
PHÒNG GD&ĐT NAM ĐÀN ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2023 - 2024 Đề chí nh th ức Môn thi: TOÁN chín h thức
Thời gian làm bài: 120 phút Câu 1: (2,5 điểm)
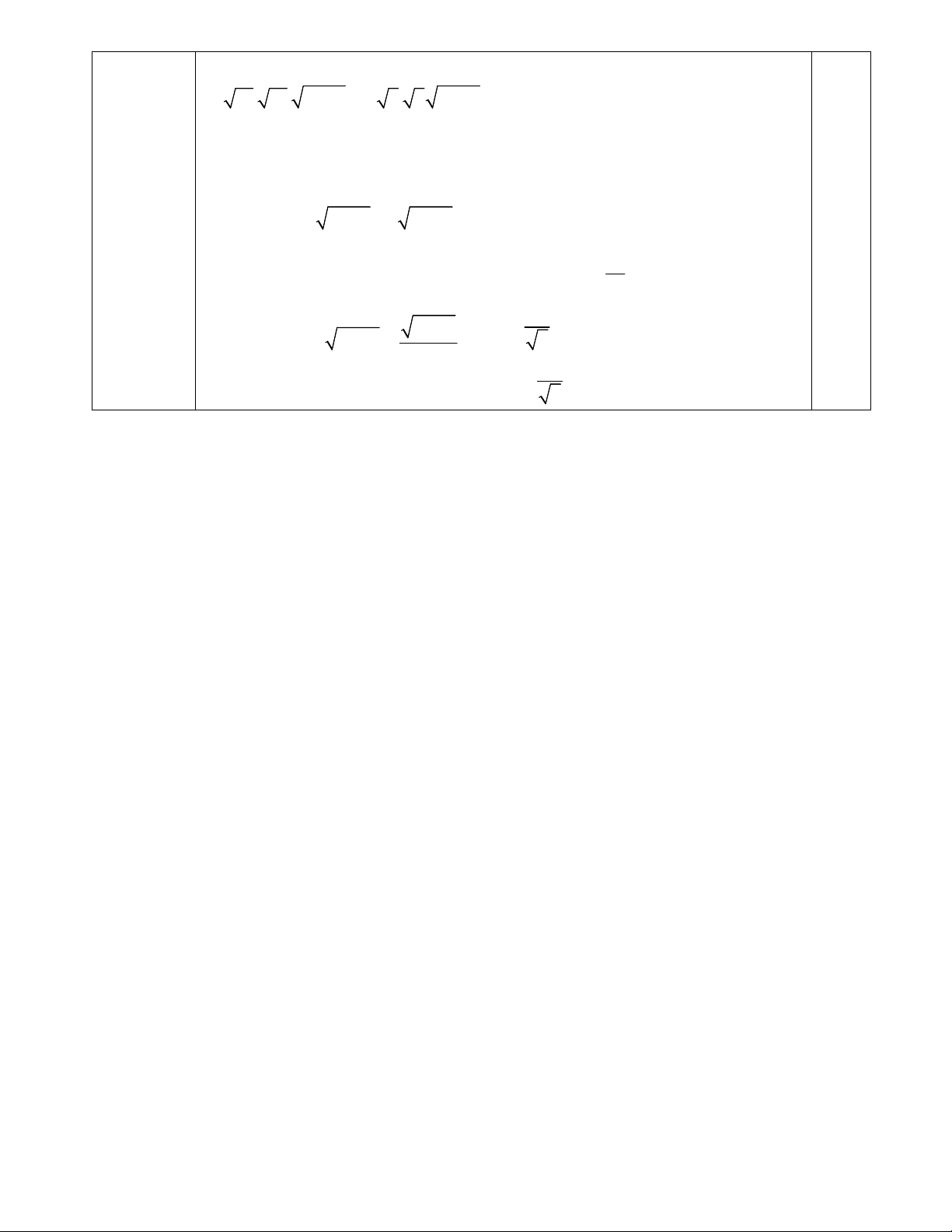
a) Tính N 3 16 2 27 6 3 b) Rút gọn biểu thức 1 a 1 M .
với a 0, a 1, a 4 a 2 a 4 a 1 .
c) Viết phương trình đường thẳng (d) song song với đường thẳng y = 3x - 3 và
cắt trục tung tại điểm có tung độ bằng -5 . Câu 2: (2,0 điểm) a) Giải phương trình: 2 2x 3x 2 0
b) Cho phương trình x2 – 5x + 3 = 0 có hai nghiệm phân biệt x1, x2. Không 2 2
giải phương trình, hãy tính giá trị của biểu thức x x 1 2 P 2 2 x x x x 1 2 1 2 Câu 3: (2,0 điểm )
a) Hai bạn Thành và Công hẹn nhau cùng xuất phát từ cổng làng để đến một địa
điểm thi THPT với chiều dài 12 km. Bạn Thành đi xe đạp điện, bạn Công đi xe máy
điện với vận tốc lớn hơn vận tốc của bạn Thành là 6 km/h. Tính vận tốc của mỗi bạn
biết bạn Công đến địa điểm thi THPT trước bạn thành 6 phút.
b) Tính diện tích tấm ni lông cần thiết để phủ kín một chiếc nón có đường kính
đáy bằng 45 cm và độ dài đường sinh là 30 cm (lấy 3,14 ). Câu 4: (3,0 điểm )
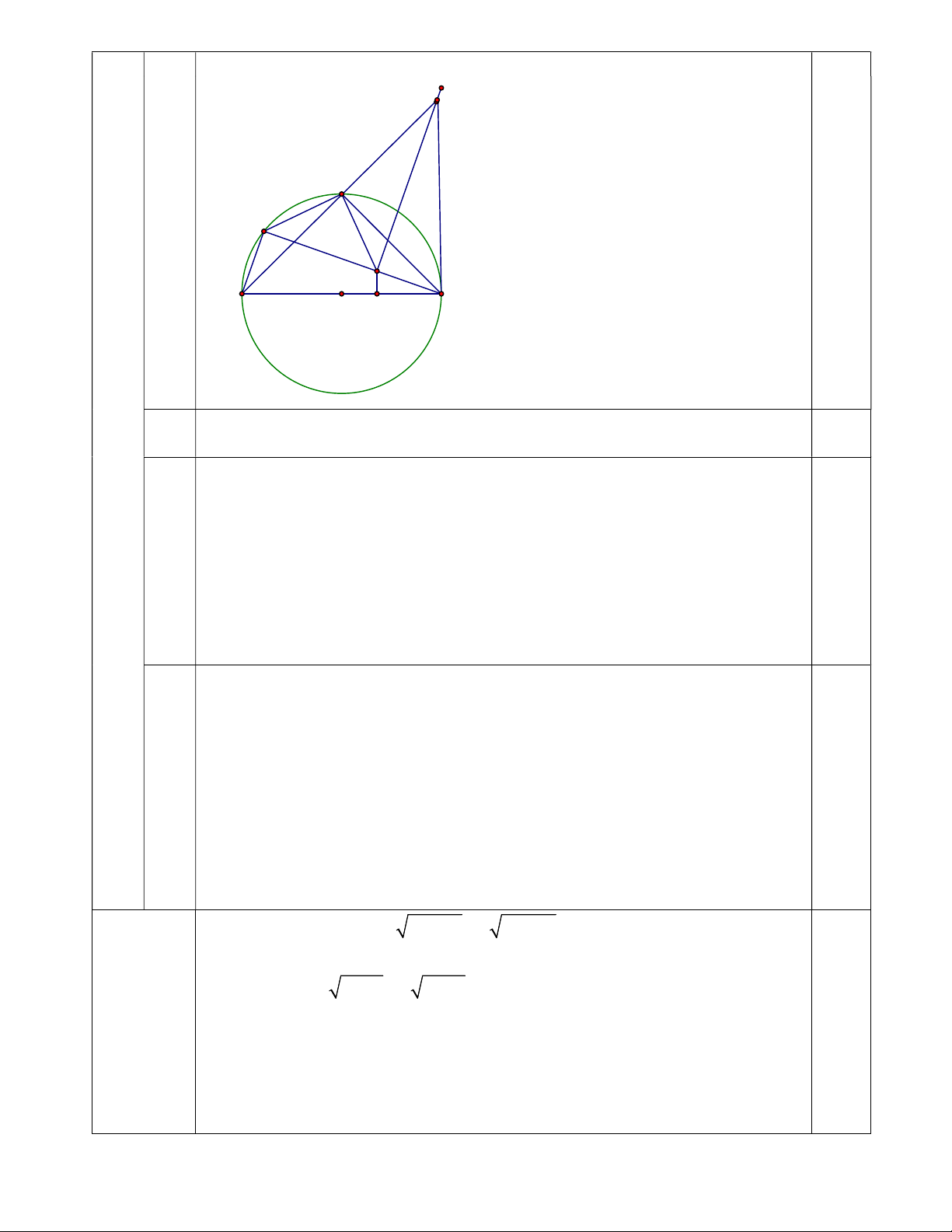
Cho đường tròn tâm O, đường kính AB. Gọi C điểm chính giữa cung AB,
Điểm D di động trên cung nhỏ AC (D khác A và C). Trên đoạn thẳng BD lấy điểm E
sao cho BE = AD, vẽ EH vuông góc với AB (H thuộc AB).
a) Chứng minh Tứ giác ADEH nội tiếp một đường tròn.
b) Chứng minh CDE vuông cân.
c) Chứng minh đường thẳng vuông góc với BD tại E luôn đi qua một điểm cố
định khi D di chuyển trên cung nhỏ AC. Câu 5 (0,5 điểm) Giải phương trình : 2 4 2 4
13 x x 9 x x 16
....................................... Hết .....................................
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
THI THỬ VÀO LỚP 10 – NĂM HỌC 2023-2024 Biểu Câu Câu Nội dung điểm a
N 3 16 2 27 6 3 = 12 6 3 6 3 12 1,0 1 a 1 M . a 2 a 4 a 1 a 2 a 1 = b .
( a 2)( a 2) ( a 2)( a 2) a 1 0,5 a 2 a 1 2( a 1) 1 2 . . = 1 ( a 2)( a 2) a 1 ( a 2)( a 2) a 1 a 4 0,5
Gọi phương trình đường thẳng cần tìm là y = a x +b (d)
Đường thẳng (d) song song với đường thẳng với đường thẳng y = 3x - 3 a 3 c 0,25 b 3
Mặt khác (d) căt trục tung tại điểm -5 => b = -5 (TM) 0,25
Vậy hàm số cần tìm là y = 3x -5.
Giải và tìm đúng nghiệm x = -2 ; x = 1/2 a 1,0 x2 – 5x + 3 = 0 2 x x 5
Vì PT có 2 nghiệm phân biệt, theo hệ thức vi ét 1 2 0,5 b x x 3 1 2 2 2 x x (x x )(x x ) x x 5 1 2 1 2 1 2 1 2 P 0,5 2 2 x x x x x x (x x ) x x 3 1 2 1 2 1 2 1 2 1 2
Gọi vận tốc của bạn Thành là x (km/h), x >0
Thì vận tốc của bạn Công là x + 6 (km/h) 0,25
Thời gian bạn Thành đi hết: 12 (giờ) x
Thời gian bạn Công đi hết: 12 (giờ) a x 6
Do bạn Công đến trước 6 phút =1/10 giờ 3 Ta có phương trình: 12 12 1 0,25 x x 6 10
Giải ra x =24 (TM) và x = -30 (KTM) 0,25
Vậy vận tốc của thành là 24km/h, của Công là 30 km/h. 0,25
Diện tích tấm ni lông là S 0,5 r l (cm2) b xq= 45 . . . .30 675 2 0,5 F C D E A B O H Vẽ hình đúng cho câu a 0,5 Ta có 0 ADE AHE a 180
=> Tứ giác ADEH nội tiếp 1,0 Xét ADC và BEC có: Có AD = BE (gt) 4
DAC EBC ( cùng chắn cung CD)
AC = BC (vì C nằm chính giữa cung AB) b
=> ADC = BEC (cgc) => CD = CE (1) và DCA ECB => 0 0,5
DCE DCA ACE ECB ACE ACB 90 (2)
Từ (1) và (2) suy ra DCE vuông cân tại C 0,5
a) Đường thẳng vuông góc với BD tại E cắt AC tại F
Vì ACB = 900 nên BCF= 900 Ta có o
BCF BEF 90 nên tứ giác BECF nội tiếp 0 0,25 c
CFB CED 45 (câu b) BAF có 0
CAB CFB 45 (Vì C nằm chính giữa cung AB) BAF vuông cân tại B.
Mà A, B cố định do đó F cố định
Vậy đường vuông góc với BD tại E luôn luôn đi qua một điểm cố định 0,25 Giải phương trình : 2 4 2 4
13 x x 9 x x 16 (1) Đk: 1 x 1 (1) <=> x x x 2 2 2 2 13 1 9 1 256 5
Áp dụng bất đẳng thức Bunhiacopxki:
13. 13. 1 x 3. 3. 3 1 x 2 2 2 13 27 2 2 13 13x 3 3x 40 2 16 10x Do đó x x x 2 2 2 2 2 2 13 1 9 1 40x (16 10x ) 0,25
Áp dụng bất đẳng thức Côsi: x x 2 2 2 16 10 16 10 64 2 2 2 x (TM ) 2 1 x Dấu bằng 1 x 5 3 2 2 2 1 0x 16 10x x (TM ) 5 0,25




