Đề thi thử Toán vào lớp 10 năm 2023 – 2024 phòng GD&ĐT Ngô Quyền – Hải Phòng

UBND QUẬN NGÔ QUYỀN
KỲ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2023 - 2024 (Đề thi gồm 02 trang) ĐỀ THI: MÔN TOÁN
(Thời gian làm bài: 120 phút không kể thời gian phát đề)
Bài 1 (1,5 điểm). Cho hai biểu thức: 2    A  2  ( 2  2 1) và   x B  1  2 .
(Với điều kiện:x  0,x  1) 2  1   x  1 x  x x    1
a) Rút gọn các biểu thức A và biểu thứcB ;
b) Tìm điều kiện của x để các giá trị của biểu thức A và B thỏa mãn:B  A  1. Bài 2 (1,5 điểm). 2 x 3 y 1  4
1. Giải hệ phương trình sau:  3 x  5 y 1  7 
2. Trong kho của một đại lý bán hàng cấp một chứa 2000 chiếc Tivi của hãng
Samsung. Do giao chỉ tiêu bán hàng, nên mỗi ngày nhân viên phải bán giao cho các đại lý
cấp hai được 50 chiếc. Gọi y (chiếc) là số Tivi còn lại trong kho sau x (ngày) bán giao.
a) Lập công thức biểu diễn hàm số y theo x ;
b) Hỏi sau 15 ngày thì số Tivi còn lại trong kho là bao nhiêu chiếc và sau bao nhiêu ngày
thì đại lý cấp một bán giao hết 2000 chiếc Tivi cho các đại lý cấp hai ? Bài 3 (2,5 điểm). 1. Cho pt bậc hai: 2
x  2(m  1)x  4m  0 (1) (Với x là ẩn,m là tham số).
a) Giải phương trình khim  0 ;
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x1,x2 thỏa
mãn: 15  2x  2x  x x  1 2 1 2 1 .
2. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một người đi xe đạp khởi hành từ thành phố A đến thành phố B cách nhau 78(km),
sau đó 1 giờ người thứ hai cũng đi xe đạp khởi hành từ thành phố B đến thành phố A, hai
người gặp nhau tại một thị trấn C cách thành phố B là 36(km). Biết vận tốc người thứ hai
đi nhanh hơn vận tốc người thứ nhất là 4 (km/h). Tính vận tốc của người thứ nhất. Bài 4 (0,75 điểm).
Theo đơn đặt hàng, một kỹ sư đã thiết kế một chi tiết
máy chất liệu bằng kim loại dạng hình trụ có bán kính
đường tròn đáy là 5 (cm), chiều cao bằng đường kính đáy.
Chi tiết máy có dạng hình trụ này được khoét rỗng hai đầu r
bằng hai nửa hình cầu như hình vẽ. Hãy tính diện tích toàn 2r 5cm
bộ bề mặt nhìn thấy của chi tiết đó ? ( lấy   3,14 ). Trang 1/2 Bài 5 (3,0 điểm).
Từ điểm M nằm ngoài đường tròn (O;R) kẻ các tiếp tuyến M , A MB của đường
tròn (O) (A và B là các tiếp điểm,OM  2R ). Gọi E là trung điểm của đoạn thẳngMB ,
C là giao điểm của đường thẳng AE với đường tròn (O) và tiaMC cắt đường tròn (O) tại điểm thứ hai D .
a) Chứng minh: tứ giácMAOB nội tiếp và   MOB  ADB ; b) Chứng minh: 2 BE  EC.EA và AD //MB .
c) Kẻ đường kính BI của đường tròn (O). Đường thẳng MI và đường thẳng AD
cắt nhau tại K . Chứng minh:KD  3KA. Bài 6 (0,75 điểm). 1 1
Cho hai số dương a và b thỏa mãn   2. Tìm giá trị lớn nhất của biểu thức: a b 1 1 T    4 2 2 2 4 2 a  b  2ab a  b  2a b
---------------------------------Hết-----------------------------
Họ và tên thí sinh: .................................................Số báo danh............................................
Cán bộ coi thi 1: …………………………… Cán bộ coi thi 1: …………......………........ Trang 2/2 UBND QUẬN NGÔ QUYỀN
HƯỚNG DẪN CHẤM BÀI THI THỬ VÀO LỚP 10
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO THPT NĂM HỌC 2023-2024 MÔN TOÁN Hướng dẫn gồm 04 trang Bài Nội dung cần đạt Điểm a) (1,0 điểm) 2  A  2  ( 2  2 1)  2  2  1 0,25 2  1
A  2  2  1  1(vì 2  1  0) 0,25   x 1 2 x  B    .  1 2   . 0,25 x  1 x  x x  1 x( x  1) x    1 Bài 1 2( x  1)( x  B  1)  2 0,25 (1,5 điểm) x( x  1)( x  1) x b) (0,5 điểm) Với x  0,x  1 2 2  Do B  A  1 =>    2 1 1 x  0 x x 0,25
 2  2 x  0(vì x  0)  x  1
Kết hợp điều kiện:x  0;x  1 với x  1 ta được: 0  x  1. 0,25 1. (0,75 điểm) 2 x 3 y 1  4 
a) Giải hệ phương trình:  3 x  5 y 1  7 
(Điều kiện:x  0;y  1) 0,25 a  x 2a  3b  4  a 1 Đặt:      b   y 1   3  a  5b  7 b   2  x 1 x 1(tm) Bài 2 =>    0,25 (1,5 điểm)  y 1  2  y  5(t ) m 
Vậy hệ phương trình có nghiệm: ( ; x y)  (1;5) 0,25 2. (0,75 điểm)
a) Công thức biểu diễn hàm số y theo x là: 0,25 y  2000  50x
b) Thay x  15 vào công thức hàm số ta có. y  2000  50.15  1250 0,25
Sau 15 trong kho còn 1250 chiếc tivi.
Do cần phải bán giao hết hàng nên thay y = 0 vào công thức ta có: 0,25 Trang 3/2
0  2000  50x  x  40
Vậy sau 40 ngày thi bán giao hết 2000 chiếc Tivi. 1. (1,5 điểm) 1.a) (0,5 điểm)
Với m  0 ta có phương trình: x 0 2
x 2x  0  x(x  2)  0  0,25 x   2
Vậy phương trình có tập nghiệm: S  0;  2 0,25 1.b) (1,0 điểm) Xét phương trình: 2
x  2(m  1)x  4m  0
  b  ac  (m  1 2 2 )  1.4m  2 m  2m  1  (m  2 ' '   1) 0,25
Do phương trình có hai nghiệm phân biệt khi: '  0  m  2 ( 1)  0  m  1 x  x  2(m 1) Theo Định lý Viet có: 1 2  0,25 x x  4m  1 2 Bài 3
Xét: 15  2x  2x  x x  1  15  2(x  x )  x x  1 2 1 2 1 2 1 2 1
(2,5 điểm)  4m 1  15 2.2(m 1)  4m  1  11  4m 11 (ĐK m  ). 0,25 4  2 16m  92m  120  0
 (m  2)(4m  15)  0 m  2(t ) m    m  15 0,25  (kt ) m  4
Vây m = 2 thảo mãn yêu cầu đề bài. 2. (1,0 điểm)
Gọi vận tốc của người đi từ A là x (km/h) (x  0) 0,25
Thời gian người đi từ A đến lúc gặp nhau là: 42 (giờ) x
Vận tốc của người đi từ B là: x  4 (km/h) 0,25
Thời gian người đi từ B đến lúc gặp nhau là: 36 (giờ) x  4
Người thứ hai đi sau người thứ nhất 1 giờ, ta có phương trình: 0,25 Trang 4/2 42  36 1 x x  4 . .  2 x 2x 168  0 x  14(t ) m
 (x 14)(x 12)  0  x    12(kt ) m
Vậy vận tốc người thứ nhất là 14km /h 0,25
Diện tích xung quanh của hình trụ là: S   2 rh   2 .5.10  100 2 . (cm ) 0,25 1
Diện tích hai nửa mặt cầu là: Bài 4 S   2 4 r   2 4 .5  10  2 0 (cm ) 0,25 (0,75 2 điểm)
Diện tích toàn bộ bề mặt nhìn thấy của chi tiết là: S  S S 1 2 0,25 S  200.
Với   3,14  S  2 628(cm )
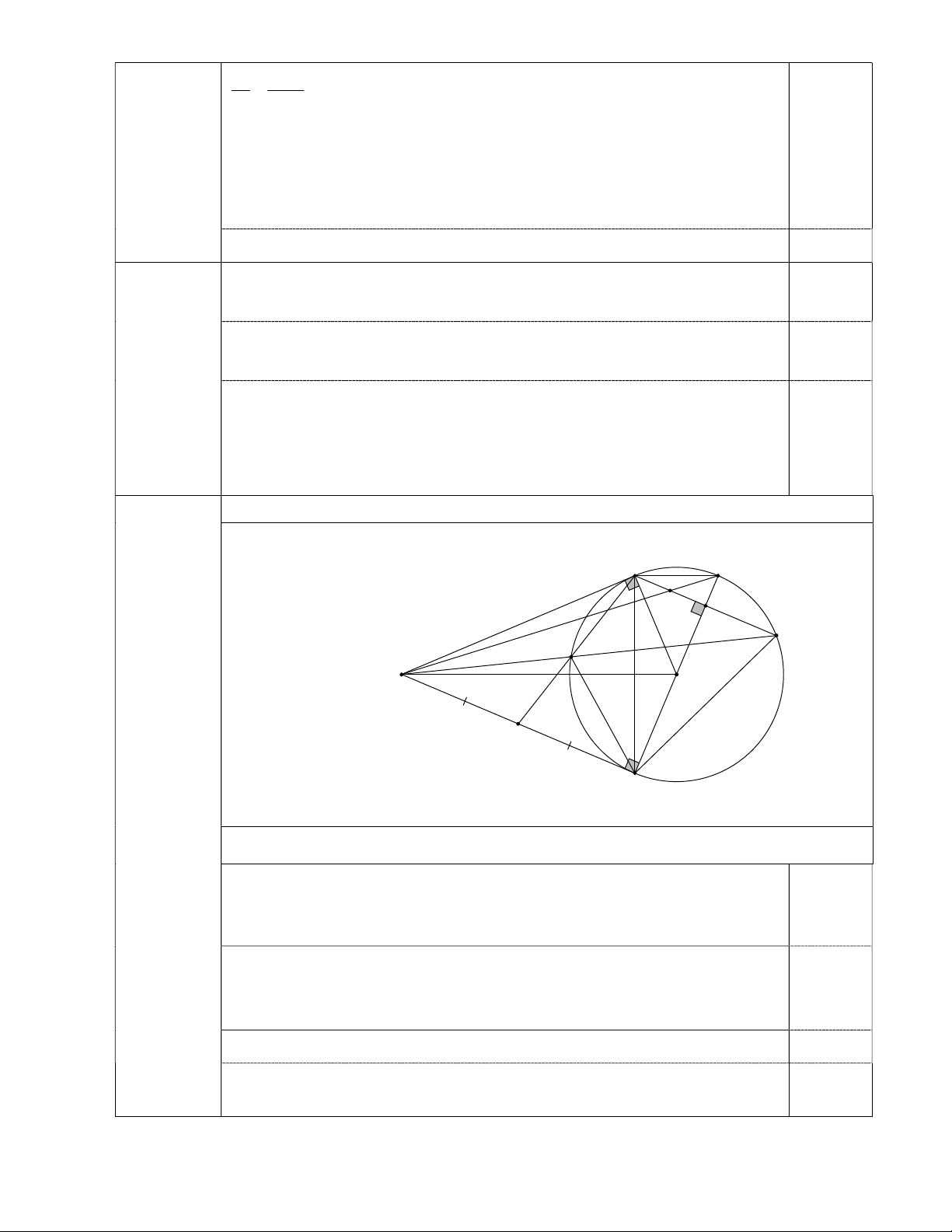
Vẽ hình đúng cho câu a; 0,25 A I K F D C M O E Bài 5 B (3,0 điểm) a) (1,0 điểm).
Ta có MA và MB là các tiếp tuyến của đường tròn (O) (A và B là
các tiếp điểm)  MA  OA, MB  OB (tính chất tiếp tuyến). 0,25   0  MAO  MBO  90 .
Xét tứ giác MAOB có   0 0 0
MAO  MBO  90  90  180 . Mà  MAO và 
MBO là hai góc đối của tứ giác MAOB . 0,25
Vậy tứ giác MAOB nội tiếp. Có  
MOB  MAB (cùng chắn cung MB của tứ giác MAOB nội tiếp) 0,25 Mà:  
ADB  MAB (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây 0,25
cung cùng chắn một cung). Trang 5/2 =>   MOB  ADB b) (1,0 điểm) Ta có:  
EBC  EAB (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây
cùng chắn cung BC của đường tròn (O)). 0,25 Xét E  BC và E  AB có:  AEB (chung);   EBC  EAB (cmt)  EBC  EAB BE EC (g.g) =>  => 2 BE  EC.EA. 0,25 EA BE Ta có 2 EB  EC.EA (cmt) EM EC Mà EB  EM (gt) 2  EM  EC.EA hay  EA EM EM EC 0,25 Xét M  EC và A  EM , có  MEA (chung);  (cmt) EA EM  M  EC  A  EM (c.g.c)    EMC  EAM Mà:  
EAM  ADM (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AC ). 0,25 =>  
EMC  ADM . Mà hai góc này ở vị trí so le trong  AD // MB . c) (0,75 điểm) Có  
DAB  MBA (hai góc so le trong). Mặt khác:  
ADB  MBA (góc nội tiếp và góc tạo bởi tia tiếp tuyến và 0,25
dây chắn cung AB của (O)) =>  
DAB  ADB => ABD cân tại B .
Gọi F là giao điểm của BI và AD . Vì BI  BM và AD // BM nên
BI  AD tại F . Mà ABD cân (cmt) có BF là đường cao đồng
thời là đường trung tuyến  F là trung điểm của đoạn AD . Có   MOB  ADB (câu a) Mà  
AIB  ADB (cùng chắn cung AB của (O)) 0,25 =>   AIB  MOD hay   AIF  MOD Xét A  FI và M  BO , ta có:   0 AFI  MBO  90 ;   AIF  MOB IF AF IF AF IF => A  FI  M  BO (g.g)      (1) OB MB 2OB 2MB IB IF KF 2KF Lại có KF // MB nên   (HQ định lý Thales) (2) IB MB 2MB 0,25
Từ (1) và (2) => AF  2KF => KD  3AK . (0,75 điểm) Bài 6
Vì a,b  0 nên áp dụng BĐT AM - GM ta có: 4 2 2 a  b  2a b . (0,75 4 2 2 2 2
 a b  2ab  2a b  2ab . 0,25 điểm) 1 1 1    . 4 2 2 2 2 a b  2ab 2a b  2ab 2a ( b a b) Trang 6/2 1 1 Tương tự:  . 2 4 2 a b  2a b 2a ( b a b) 1 1 1 Khi đó: T    . 2a ( b a b) 2a ( b a b) a ( b a b) 1 1 Theo đề bài 
 2  a b  2ab mà cũng theo BĐT AM-GM a b 0,25 1 1 1 1 1 1   2. .  2  2.   1. a b a b ab ab 1 1 1 Suy ra: T  
 . Dấu “=” xảy ra  a  b  1.  2 a ( b a b) 2(ab) 2 1
Vậy giá trị lớn nhất của T là  a  b  1. 0,25 2 Chú ý:
- Trên đây chỉ trình bày tóm tắt một cách giải, nếu thí sinh làm theo cách khác mà
đúng thì cho điểm tối đa ứng với điểm của câu đó trong biểu điểm.
- Thí sinh làm đúng đến đâu cho điểm đến đó theo đúng biểu điểm.
- Trong một câu, nếu thí sinh làm phần trên sai, dưới đúng thì không chấm điểm
- Bài hình học, thí sinh vẽ hình sai thì không chấm điểm. Thí sinh không vẽ hình mà
làm vẫn làm đúng thì cho nửa số điểm của các câu làm được.
- Bài có nhiều ý liên quan với nhau, nếu thí sinh công nhận ý trên để làm ý dưới mà thí
sinh làm đúng thì chấm điểm ý đó.
- Điểm của bài thi là tổng điểm các câu làm đúng và không được làm tròn. Trang 7/2