


Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
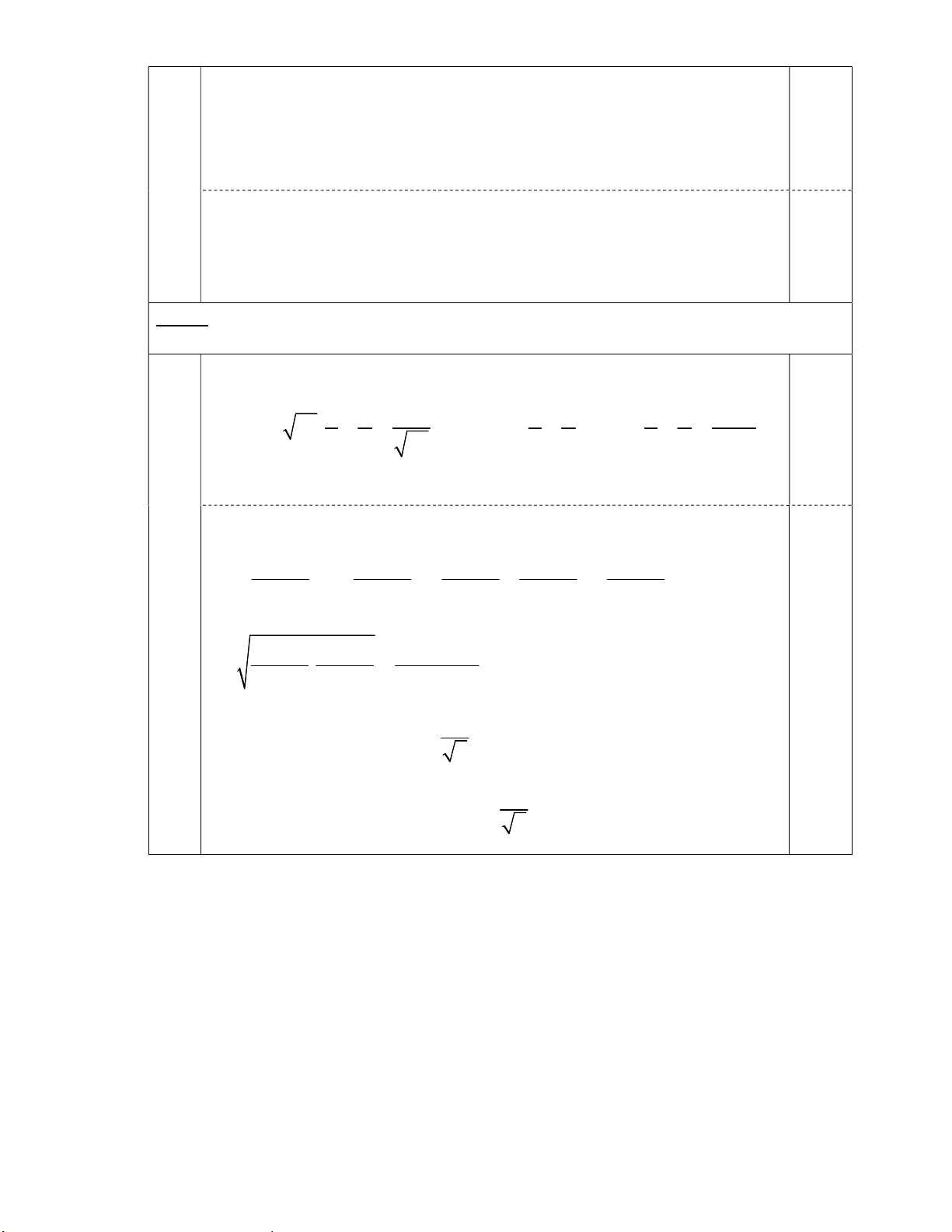
KỲ THI THỬ VÀO LỚP 10 THPT THÀNH PHỐ VINH NĂM HỌC 2023-2024 HƯỚNG DẪN CHẤM Môn: Toán Câu Nội dung Điểm Bài 1: (2,5 điểm ) A 2 48 3 75 2 108 a A 8 3 15 3 12 3 0,5 A 11 3 . 0,5 2x 3y 2 2 2x 3 2y 4 0,25 2x 2y 2 2x 2y 2 3 2 4 2y 6 y 4 0,25 2x 2y 2 2x 2y 2 b 3 2 y 4 0,25 1 x 4
Vậy hệ phương trình có nghiệm 1 3 2 ; . 0,25 4 4
Vì đồ thị hàm số y ax b cắt trục tung tại điểm có tung độ bằng 3 0,25 nên b 3.
Mặt khác, đồ thị hàm số y ax b đi qua điểm ( A 2; 5 ) nên ta có: c 5 2a b Hay 5 2a 3 0,25 a 4 Vậy a 4 ; b 3 Bài 2: (2,0 điểm ) 2
' 1 4.3 13 0 0,25
Suy ra phương trình có hai nghiệm phân biệt: 1 13 x 0,25 1 3 a 1 13 x 0,25 1 3 Vậy 1 13 1 13 S ; 0,25 3 3 b
Vì x là nghiệm của phương trình 2
2x 5x 2 0 , nên ta có: 0,25 2 2 2x 5x 2 0 2 2 Hay 2 2x 5 5x 3. 2 2 Khi đó 5x 3 5x 3 1 2 M . x x 2 1 0,25 5 2 2 x x 3 x x 5 x x 10x x 3 x x 1 2 1 2 1 2 2 1 2 1 2 M x x x x 1 2 1 2
Theo định lí Vi-ét ta có: 5 x x 1 2 2 0,25 x .x 1 1 2 2 5 5 5. 10. 1 3. 0,25 Suy ra: 2 2 135 M 1 4 Bài 3: (2,0 điểm)
Gọi giá cước mức 2, mức 3 của loại xe đó lần lượt là x(đồng/km), y 0,25
(đồng/km). ĐK: x 0; y 0 .
Cô Thủy đi 28 km bao gồm: 1 km mức 1; 24 km mức 2 và 3 km mức
3 hết số tiền 429500 nên ta có: 0,25
20000 24.x 3y 429500 24x 3y 409500 (1)
Chú Tuấn đi 33 km bao gồm: 1 km mức 1; 24 km mức 2; 8 km mức 3
hết số tiền 492000 nên ta có: 0,25 a
20000 24.x 8y 492000 24x 8 y 472000 (2)
Từ (1) và (2) ta có hệ phương trình 24x 3y 409500 0,25 24x 8y 472000 5 y 62500 x 15500 (TM) 0,25 24x 3y 409500 y 12500
Vậy giá cước mức 2: 15500 đồng/km; mức 3: 12500 đồng/km. 0,25
Diện tích xung quanh của cốc giấy hình trụ là: .6.7 131,88 (cm2) 0,25 Diện tích đáy cốc là: 2 .3 28, 26 (cm2) b
Diện tích giấy để làm 100 chiếc cốc là:
100.131,88 56,52 16014 (cm2) Đổi 16014 cm2 = 1,6014 m2. 0,25
Làm tròn kết quả đến chữ số thập phân thứ hai ta được 1,6 m2.
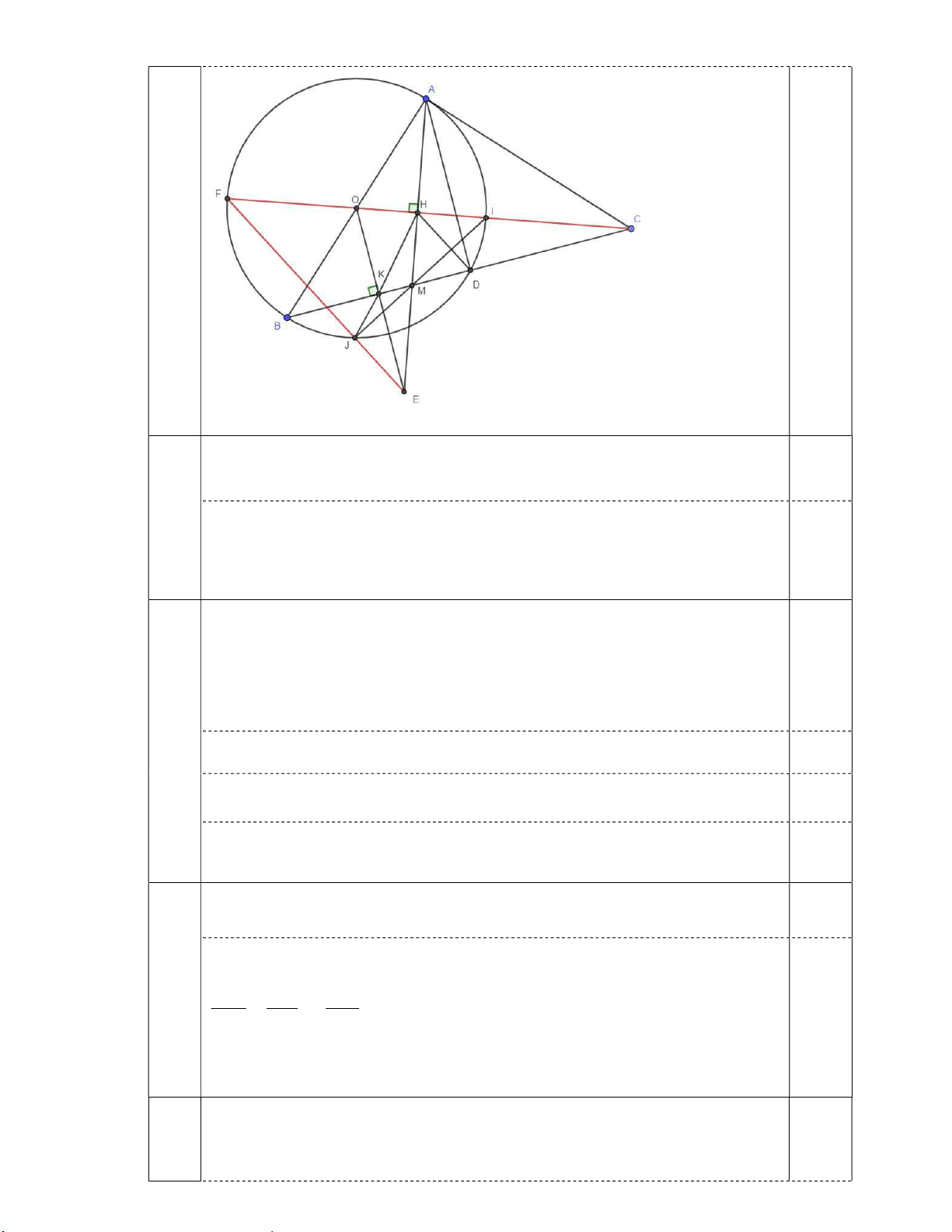
Vậy để làm 100 chiếc cốc cần 1,6 m2 giấy. Bài 4: (3,0 điểm) 0,5 Vẽ hình xong câu a) Xét tứ giác : 90o ACDH ADC
(vì AB là đường kính của đường tròn 0,5 (O)). a 90o ADC AHC 0,5
Suy ra tứ giác ACDH nội tiếp. + Xét O
AC vuông tại A, đường cao OH 2 CH.CO CA 0,25 + 2 CAD ∽ CBA CA C . D CB b Suy ra CH.CO C . D CB C HD ∽ C BO 0,25 CHD CBO HOBD nội tiếp. 0,25 Do đó CHD OBD ODB OHB BHM DHM hay HM là tia 0,25 phân giác của góc BHD.
Xét tam giác HBD có HM là phân giác trong và HM HC nên HC 0,25
là đường phân giác ngoài. Từ đó suy ra c MD CD HD MB CB HB 0,25 M . D BC M . B CD .
Gọi F là giao điểm của tia CO với đường tròn (O). d 0,25 Khi đó 2
HMC ∽ HOE HM .HE H . O HC HA HI.HF H MI ∽ H FE HFE HMI . Mà 180o HFJ HMI HMJ 0,25 HFE
HFJ F, J , E thẳng hàng. Từ đó suy ra ĐPCM. Bài 4: (0,5 điểm)
+ Áp dụng BĐT Cô si cho hai số dương x, y 1 1 2 x y xy x y 1 1 1 1 4 2 ; 4 0,25 x y xy x y x y x y (1)
+ Áp dụng (1) và BĐT Cô si 2 2 2 2 2 2 b c 4 b c a 3a 2 M a . 2 2 2 2 2 2 2 2 a b c a b c b c b c a 3 2 2 2 2 2 b c 2 . 5 2 2 2 2 2 a b c b c 0,25 a
Dấu bằng xảy ra khi b c . 2 a
Vậy M nhỏ nhất bằng 5 khi b c . 2
Lưu ý: Học sinh giải cách khác đúng vẫn cho điểm tối đa
Document Outline
- Doc1
- HDC thi thử môn Toán năm học 2022-2023-đã nén




