ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT
Năm học: 2023 - 2024 Môn: TOÁN Ngày thi: 17/05/2023
Thời gian làm bài: 120 phút, không kể thời gian giao đề
(Đề này gồm có 05 câu, 01 trang)
Câu 1. (2,0 điểm)
1) Giải phương trình: x  12  3x x  y  2
2) Giải hệ phương trình sau:  3
 x  4y  3
Câu 2. (2,0 điểm)     
1) Rút gọn biểu thức: A = 2a a 11 a 3 1    :
với a  0, a  4, a  9 a  5 a  6 a  2 a  3  
2) Trong mặt phẳng toạ độ Oxy , cho đường thẳng (d): y  2x – 3 và đường thẳng
(d’): y  2m  5 x  3 . Tìm m để (d) và (d’) cắt nhau tại điểm P có hoành độ bằng  2
Câu 3. (2,0 điểm)
1) Một tàu hoả đi từ A đến B dài 40 km. Khi đi đến địa điểm B, tàu dừng lại 20
phút rồi đi tiếp 30 km nữa để đến địa điểm C với vận tốc lớn hơn vận tốc khi đi từ A đến
B là 5 km/h. Tính vận tốc của tàu hoả khi đi trên quãng đường AB, biết thời gian kể từ
khi tàu hoả xuất phát từ địa điểm A đến khi tới địa điểm C hết tất cả 2 giờ. 2) Cho phương trình: 2
x  2(m 1)x  2m  3  0 (x là ẩn, m là tham số).
Xác định các giá trị của m để phương trình có 2 nghiệm phân biệt x ; x thỏa mãn 1 2 2 2 x x 1 2 
 5x  x . 2 1  x x 2 1
Câu 4. (3,0 điểm)
Cho tam giác ABC (AB < AC) có ba góc nhọn. Đường tròn tâm O đường kính BC
cắt các cạnh AC, AB lần lượt tại D, E. Gọi H là giao điểm của BD và CE; F là giao điểm của AH và BC.
1) Chứng minh ADHE là tứ giác nội tiếp được đường tròn.
2) Gọi M là trung điểm của AH; AF cắt ED tại K. Chứng minh MD là tiếp tuyến
của đường tròn (O) và MD2 = MK. MF
3) Chứng minh BK vuông góc với MC.
Câu 5 .(1,0 điểm)
Cho a, b, c là các số thực dương.  ab bc  1 1  a b c Chứng minh          a  b b  c   a  b b  c  b  c c  a a  b
---------- Hết --------- HƯỚNG DẪN CHẤM
ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT
Năm học: 2023 - 2024 Môn: TOÁN
( Đáp án gồm 05 trang ) Câu Phần Đáp án Điểm
Giải phương trình: x 12  3x 1 1,0
Điều kiện 3x  0  x  0 0,25
 x 12  3x
x 12  3x   0,25 x 12  3  x 1  2  x 12 x  6      0,25  4x 12  x  3
Đối chiếu với điều kiện kết luận nghiệm x = 3 0,25 Câu1
*Lưu ý: HS không tìm đk x  0 và giải ra được x = 6 ; x=3 là
nghiệm của PT hoặc chỉ có 1 nghiệm thì cho 0,5 điểm (2,0    đ x y 2 iểm)
Giải hệ phương trình sau:  1 1,0 3
 x  4y  3 x  y  2 x  y  2    3
 x  4y  3 3 
( y  2)  4 y  3 0,25 2 x  y  2 x  y  2     3
 y  6  4y  3  y  3  0,25 x  y  2 x  5      y  3  y  3 0,25
Vậy hệ phương trình có nghiệm (x; y) = (5; 3) 0,25
 2a  a 11 a  3  1  
Rút gọn biểu thức: A =  : a  5 a  6 a  2 a  3   1,0
với a  0,a  4, a  9 Câu2     a  a 
 a 3 a 3 2 11  1    (2,0 A = 
 a  2 a  3 :    đ a 2 a 3 iểm) 1  0,25
2a  a 11  a  9 1 = :
 a 2 a 3 a 3   a a 2 1 = : 0,25
( a  2).( a  3) a  3
( a  2).( a  1) = . a  3 0,25   ( a 2).( a 3)  a  1 0,25
Trong mặt phẳng toạ độ Oxy, cho đường thẳng (d): y  2x – 3
và đường thẳng (d’): y  2m  5 x  3 . Tìm m để (d) và (d’) 1,0
cắt nhau tại điểm P có hoành độ bằng  2 Để 3
(d) và (d’) cắt nhau thì 2m  5  2   m  0,25 2 2 Thay x  2
 vào PT đường thẳng (d) ta có y 1 0,25
Suy ra hai đường thẳng (d) và (d’) cắt nhau tại điểm P ( 2  ;1) Thay x  2
 ; y 1 vào PT đường thẳng (d’) ta được 0,25 1  4
 m 10  3  m  3
Đối chiếu với ĐK và kết luận m =3 thỏa mãn đề bài 0,25
Một tàu hoả đi từ A đến B dài 40 km. Khi đi đến địa điểm B, tàu
dừng lại 20 phút rồi đi tiếp 30 km nữa để đến địa điểm C với
vận tốc lớn hơn vận tốc khi đi từ A đến B là 5 km/h. Tính vận 1,0
tốc của tàu hoả khi đi trên quãng đường AB, biết thời gian kể từ
khi tàu hoả xuất phát từ địa điểm A đến khi tới địa điểm C hết tất cả 2 giờ.
Gọi vận tốc của tàu hỏa khi đi trên đoạn đường AB là
x(km / h) . ĐK x  0
Vận tốc của tàu hỏa trên đoạn đường BC là x  5(km / h) 40 0,25 1
Thời gian tàu đi trên đoạn đường AB là (h) (1,0) x 30 Câu3
Thời gian tàu đi trên đoạn đường BC là (h) x  5 2điểm
Vì tàu đi từ A đến C hết tất cả 2 giờ (tính cả thời gian nghỉ 20 40 30 1 0,25 phút) nên ta có PT    2 x x  5 3 2    40 30 5 120x 600 90x 5x 25x      x x  5 3 3x(x  5) 3x(x  5) 0,25 2 2          120x 600 90x 5x 25x 5x 185x 600 0
Giải PT được x  40(t/m) ; x  3 (loại) 1 2
Vậy vận tốc của tàu trên đoạn đường AB là 40 km/h 0,25 Cho phương trình: 2
x  2(m 1)x  2m  3  0 (x là ẩn, m là
tham số). Xác định các giá trị của m để phương trình có 2 1,0 2 2 x x 1 2
nghiệm phân biệt x ; x thỏa mãn 
 5x  x . 2 1  1 2 x x 2 1 Ta có   m 
 m   m  m   m  2 ' 2 2 ( 1) 2 3 4 4 2
Để phương trình có 2 nghiệm phân biệt thì ∆’ > 0  m  22 2  0  m  2  0,25
x  x  2m  2 Theo Vi-ét ta có 1 2 
x x  2m  3  1 2 2 2 Đẳ x x ng thức 1 2 
 5x  x có nghĩa khi 2 1  x x 2 1  0,25 x  0 3 1 
 x x  0  2m  3  0  m  1 2 x  0 2  2 2 2 x x Theo đề bài: 1 2 
 5x  x 2 1  x x 2 1 3 3 x x
5(x  x )x x 1 2 2 1 1 2    x x x x x x 1 2 1 2 1 2 0,25 3 3
 x  x  5(x  x )x x  0 1 2 2 1 1 2
  x  x  2 2
x  x x  x
 5(x  x )x x  0 1 2 1 1 2 2  1 2 1 2
 x  x  2 2
x  x  6x x  0 1 2 1 2 1 2 
Vì pt có 2 nghiệm phân biệt  x  x  x  x  0 1 2 1 2 Suy ra 2 2
x  x  6x x  0 1 2 1 2
 x  x 2  4x x  0 1 2 1 2
 2m  22  42m  3  0 0,25 2
 4m  8  0  m   2 TM 
Vậy m   2 là giá trị cần tìm
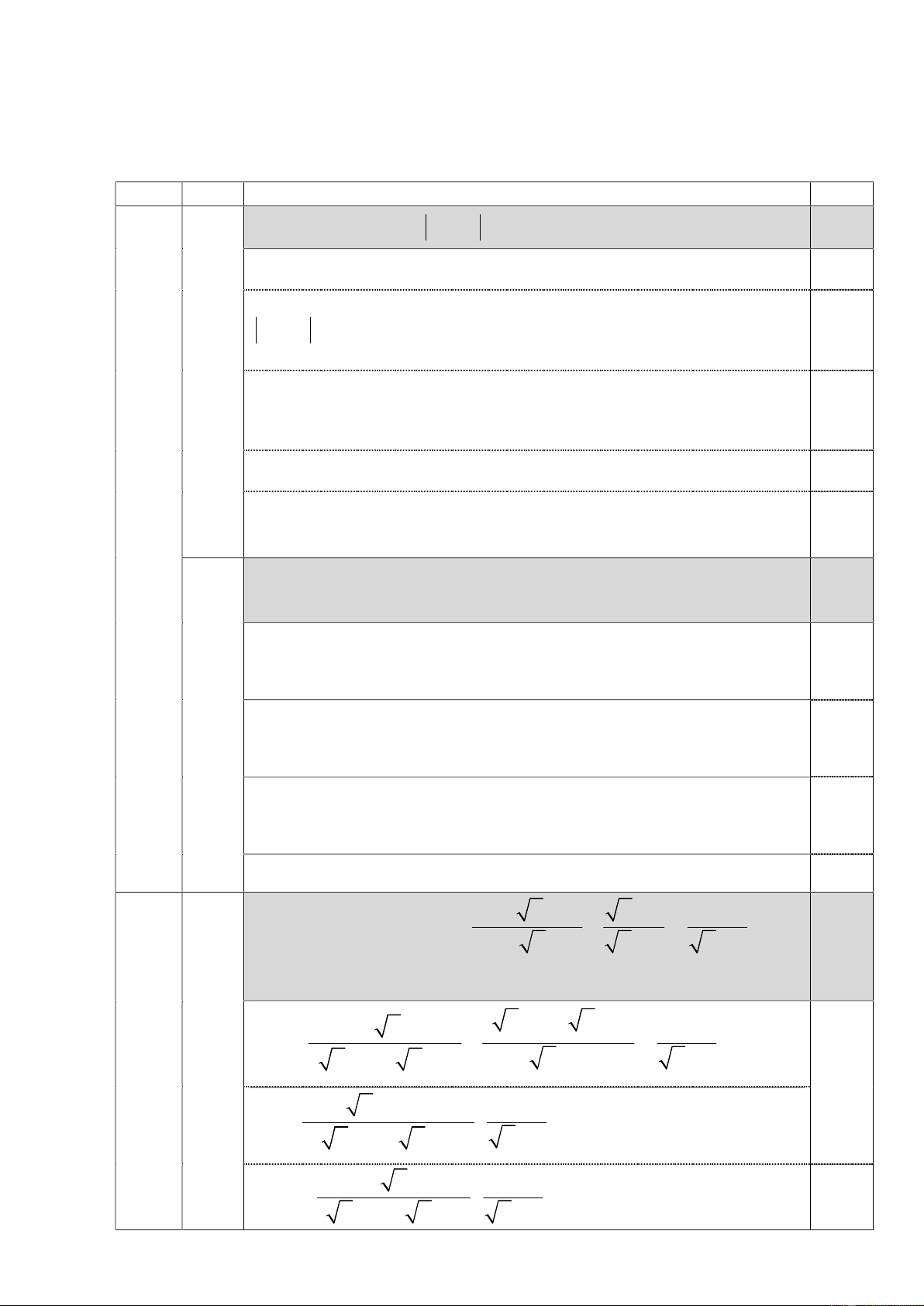
Cho tam giác ABC (AB < AC) có ba góc nhọn. Đường tròn tâm O đường
kính BC cắt các cạnh AC, AB lần lượt tại D, E. Gọi H là giao điểm của
BD và CE; F là giao điểm của AH và BC.
1) Chứng minh ADHE là tứ giác nội tiếp được đường tròn 3,0
2) Gọi M là trung điểm của AH, AF cắt ED tại K.
Chứng minh MD là tiếp tuyến của đường tròn (O) và MD2 = MK. MF
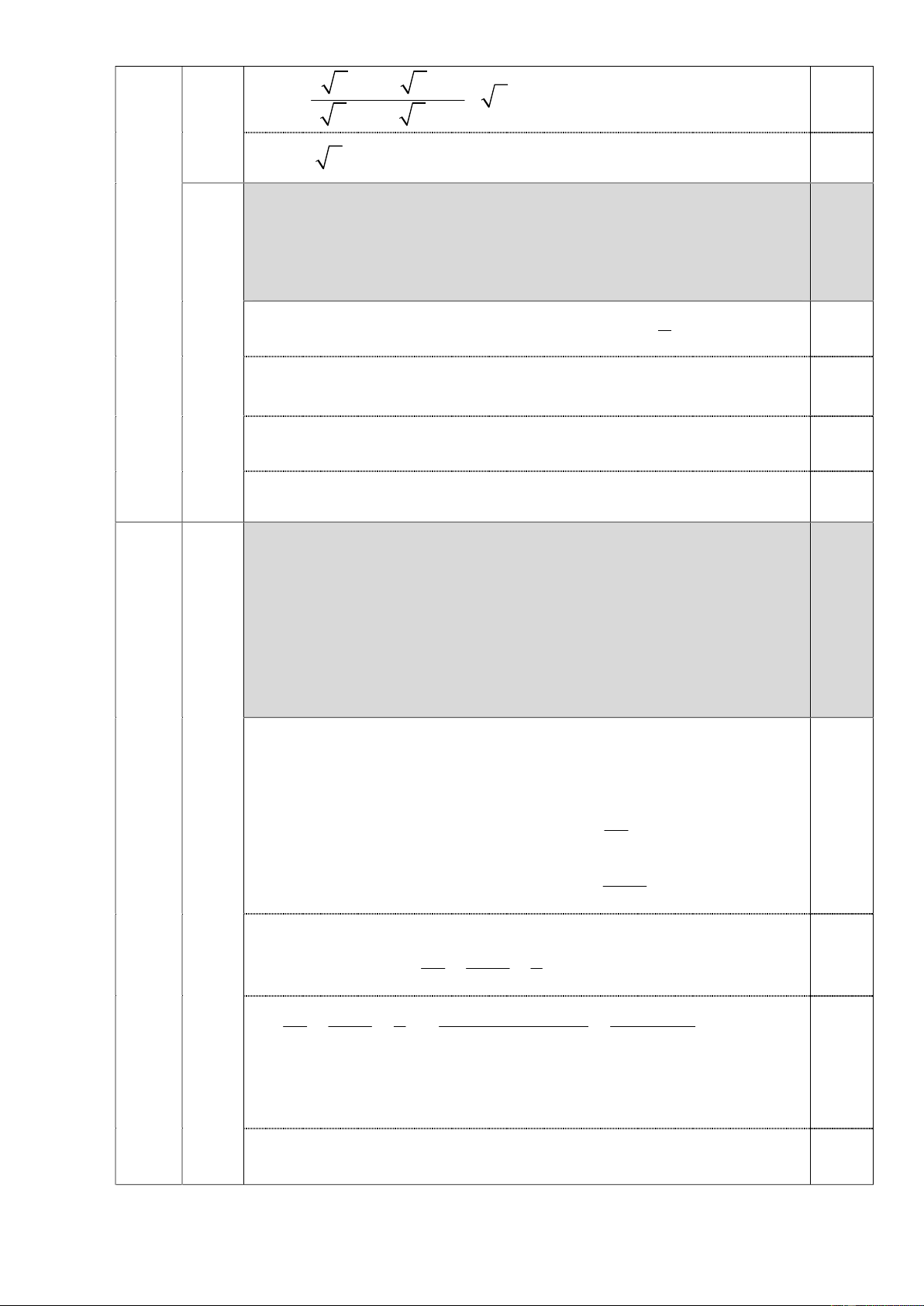
3) Chứng minh BK vuông góc với MC A D E H B C F O Câu4 (3,0
Vẽ hình ý 1 được 0,25đ điểm) A 0,25 M D I K E H B C F O  0   Ta có 0 BEC
90 , BFC  90 (góc nội tiếp chắn nửa đường tròn)  0   0,25 Suy ra 0 ADH 90 , AEH  90 1  ADH   0 0 0    Xét tứ giác ADHE có AEH 90 90 180 (0,75) 0,25
Mà hai góc này ở vị trí đối nhau nên tứ giác ADHE nội tiếp một đườ 0,25 ng tròn.
+) Xét tam giác ADH vuông tại D có DM là trung tuyến 0,25    MDH  
MD = MH = MA  MDH cân tại M MHD
Lại có tam giác BOD cân tại O nên  ODB   OBD
            0 MDH ODH MHD OBH BHF OBH  90  0,25 Do vậy 0 MDO  90 hay MD  OD 2
Lại có D thuộc (O) nên MD là tiếp tuyến của (O)
(1,0) +) Vì H là trực tam của tam giác ABC nên AF  BC    Ta có 0 HFC
HDC  180 nên HFCD là tứ giác nội tiếp  MDK   Lại có DCE (cùng chắn cung DE) 0,25  DCE   Mà MFD (cùng chắn cung HD)  MDK   Suy ra
MFD . Do đó MDK ∽ MFD(g.g) MD MK 2    MD  MF.MK 0,25 MF MD
Chứng minh BK vuông góc với MC
Gọi I là giao điểm của MC và (O) 0,25 C/m 2
MD  MI.MC  MI.MC  MK.MF 3 C/m MIK ∽ M C F (c.g.c) 0,25 (1,0)     0 MIK MFC  90  IK  MC (1) 0,25  Lại có 0 BIC  90  IB  MC (2) 0,25
Từ (1) và (2) suy ra B, I, K thẳng hàng. Hay BK  MC .
Cho a, b, c là các số thực dương. Chứng minh  1,0 ab bc  1 1  a b c          a  b b  c   a  b b  c  b  c c  a a  b Chứng minh được: ab bc  ab bc   a c    2   2b  .     a  b b  c  a  b b  c   a  b b  c  0,25 1 1 1 1  1 1  Mặt khác:     2  .   a  b b  c a  b b  c  a  b b  c  Câu5  a c  1 1   a c  b b  (1,0 VT  2 b    2    2.       đ
 a b bc a b bc
 a b bc a b bc 0,25 iểm) (1) a a 2a 2a Lại có:    b  c a b  c a  b  c a  b  c 0,25 a b c Tương tự ta suy ra VP     2 . (2) b  c c  a a  b
Dấu “=” của (2) không xảy ra nên VP > 2 (3) 0,25 Từ (1) và (3) suy ra đpcm
* Lưu ý: Học sinh làm bài đúng theo cách khác vẫn cho điểm tối đa.