TRƯỜNG THCS LÊ LỢI
KỲ THI THỬ VÀO LỚP 10 THPT
Năm học: 2023 – 2024 Đề A Môn thi: Toán
Thời gian làm bài: 120 phút không kể thời gian giao đề
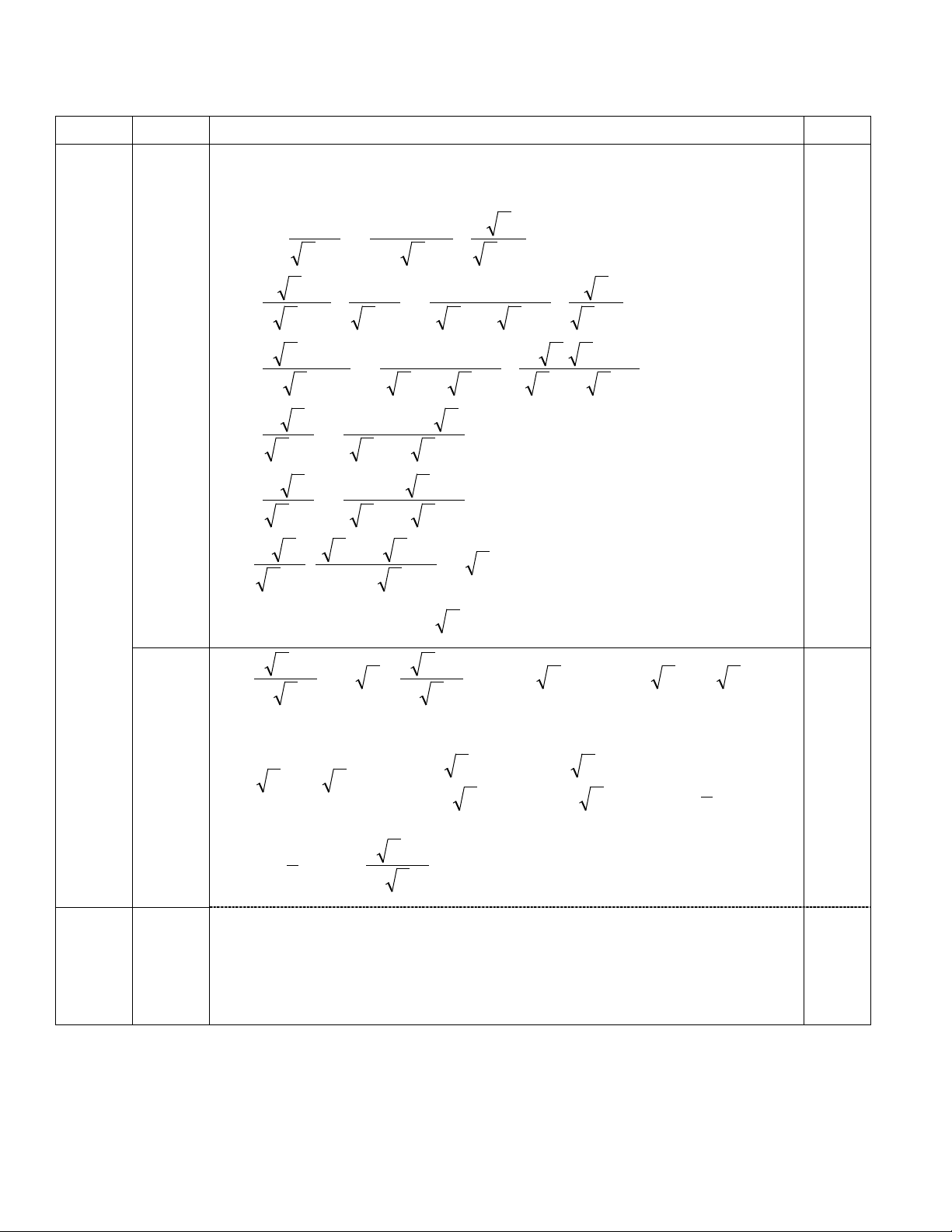
Câu 1: (2,0 điểm)  3   x + 2  = 3+  : x P  −   x 1    x x 2 x 2  − + − + 
1. Rút gọn biểu thức P
2. Tìm các giá trị của x để 4 x P −1 = x
Câu 2 (2,0 điểm).
1. Giải hệ phương trình sau: 3x + 2y = 9 
x − 4y = −11
2. Cho hàm số: y = ax +b. Tìm a, b biết đồ thị của hàm số đã cho song song với đường thẳng
(d ): y = 3x – 5 và đi qua giao điểm Q của hai đường thẳng (d ): y = 2x - 3; (d ): y = - 3x + 2. 1 2 3
Câu 3 (2,0 điểm)
1. Giải phương trình sau: 2x2 + 3x - 5 = 0
2. Tìm các giá trị của tham số m để phương trình 2 2
x − 2(m −1)x + m = 0 có hai nghiệm phân
biệt x ,x thỏa mãn hệ thức (x − x + 6m = x − 2x . 1 2 )2 1 2 1 2 Câu 4: (3,0 điểm)
Cho tam giác ABC nhọn (AB < AC). Đường cao BD, CE cắt nhau ở H. DE cắt BC ở F. M là
trung điểm của BC. Chứng minh rằng:
1) Tứ giác BEDC là tứ giác nội tiếp. 2) FE. FD = FB. FC. 3) FH vuông góc với AM.
Câu 5: (1,0 điểm ) Cho các số thực không âm x,y,z thỏa mãn: x2 + y2 + z2 ≤ 3y
Tìm GTNN của biẻu thức: 1 4 8 P = ( x + ) + + 2 1
(y + 2)2 (z + 3)2
-----------------------------------Hết--------------------------------- HƯỚNG DẪN CHẤM ĐỀ A Câu Ý
Lời giải (vắn tắt) Điểm I 1)
a) ĐKXĐ: x ≥ , 0 x ≠ 1 0.25 (2,0đ) (1.0đ)  3   x + 2  = 3 +  : x P  −   x 1    x x 2 x 2  − + − +   ( 3 x − ) 1 3   x + 2 x  P = + : −   x −1 x −1 
  ( x + 2)( x − ) 1 x + 2 
 3 x − 3 + 3  x + 2 x( x − )  P 1 = : − 0.25   x −1  
  ( x + 2)( x − )
1 ( x + 2)( x − ) 1 
 3 x   x + 2 − x + x  P = : 0.25   x −1 
  ( x + 2)( x − ) 1   3 x   2 + x  P = :   x −1 
  ( x + 2)( x − ) 1 
3 x ( x + 2)( x − ) P 1 = ⋅ = 3 x x −1 2 + x Vậy với x ≥ ,
0 x ≠ 1 thì P =3 x 0,25 4 x −1 4 x −1 P = ⇔ 3 x =
⇒ 3x − 4 x +1 = 0 ⇔ ( x − ) 1 (3 x − ) 1 = 0 0,25 x x x =  x −1 = 0  1 2) ( x 1 x − ) 1 (3 x − ) =  1 = 0 ⇔  ⇔  ⇔ 1 1,0 đ  3 x −1 = 0 3 x = 1 x =  0,5  9
x=1 không thỏa mãn ĐKXĐ. Vậy 1 4 − x x = P 1 = 9 thì x 0,25 2 1 3x + 2y = 9 6x + 4y = 18 7x = 7 x = 1 x = 1 (2,0đ) (1đ)  ⇔  ⇔  ⇔  ⇔  0.5
x − 4y = −11
x − 4y = −11 3x + 2y = 9  1 . 3 + 2y = 9 y = 3
Vậy hệ phương trình có một nghiệm duy nhất (x;y)=(1;3) 0.5
2)Vì đồ thị hàm số y = ax +b song song với đường thẳng (d ): y = 3x – 5 2 1 0.75 (1đ) Nên a = 3; b ≠ 5 −
Vì Q là giao điểm của hai đường thẳng (d ): y = 2x - 3; (d ): y = - 3x + 2 2 3
nên tọa độ của điểm Q là nghiệm của hệ phương trình  y = 2x − 3 x = 1  ⇔  y 3x 2  = − +  y = 1 − => Q( 1 ; -1)
Do đồ thị hàm số đã cho đi qua Q nên - 1 = 3 + b => b = - 4 thỏa mãn b ≠ 5 −
Vậy a = 3, b = - 4 thỏa mãn bài toán. 0,25 3 1 2 2 x + 3x − 5 = 0
(2,0đ) (1,0đ) Vì a=2;b=3;c=-5 nên a+b+c=2+3+(-5)=0 0,25 − 5 0,5
Vậy phương trình có hai nghiệm phân biệt x = x = 1 ; 1 2 2 0,25 2 2 2 x − 2(m −1)x + m = 0 (1,0đ) Ta có: ∆ = −  ( − ) 2 2 ' m 1  − m  2 2 = m − 2m +1− m =1− 2m
Phương trình có hai nghiệm phân biệt x ,x 1
⇔ ∆' > 0 ⇔ 1− 2m > 0 ⇔ m < 1 2 2 x + x = 2 m −1 0,25 1 2 ( ) Theo vi-ét ta có:  2 x x =  m 1 2 Theo đề bài ta có:
(x − x )2 + 6m = x − 2x ⇔ (x + x − 4x x + 6m = x − 2x 1 2 )2 1 2 1 2 1 2 1 2 ⇔ 4(m − )2 2
1 − 4m + 6m = x − 2x ⇔ 2m − + 4 = x − 2x 1 2 1 2 0,25
Khi đó kết hợp với x + x = 2 m −1 ta có hệ pt: 1 2 ( )  4  4 x = m − 2 x = m − 2  x + x = 2 m −1  3x = 4m − 6   1 2 ( ) 2 2  3  3 2  ⇔  ⇔  ⇔ Thay x − 2x = 2m − + 4 x + x = 2m − 2 4 2 1 2 1 2 x 2m 2 m 2  = − − + x = m 1 1  3  3 0,25  4 x = m − 2  2  3  vào 2 x x = m ta được: 2 1 2  x = m 1  3  4  2 1 − 4  1 4   m = 0 2 2 m − 2
. m = m ⇔ m − m = 0 ⇔ −m m + =  0 ⇔  (tm)  3  3 9 3  9 3   m = 12 − Vậy m = 0;m = 1
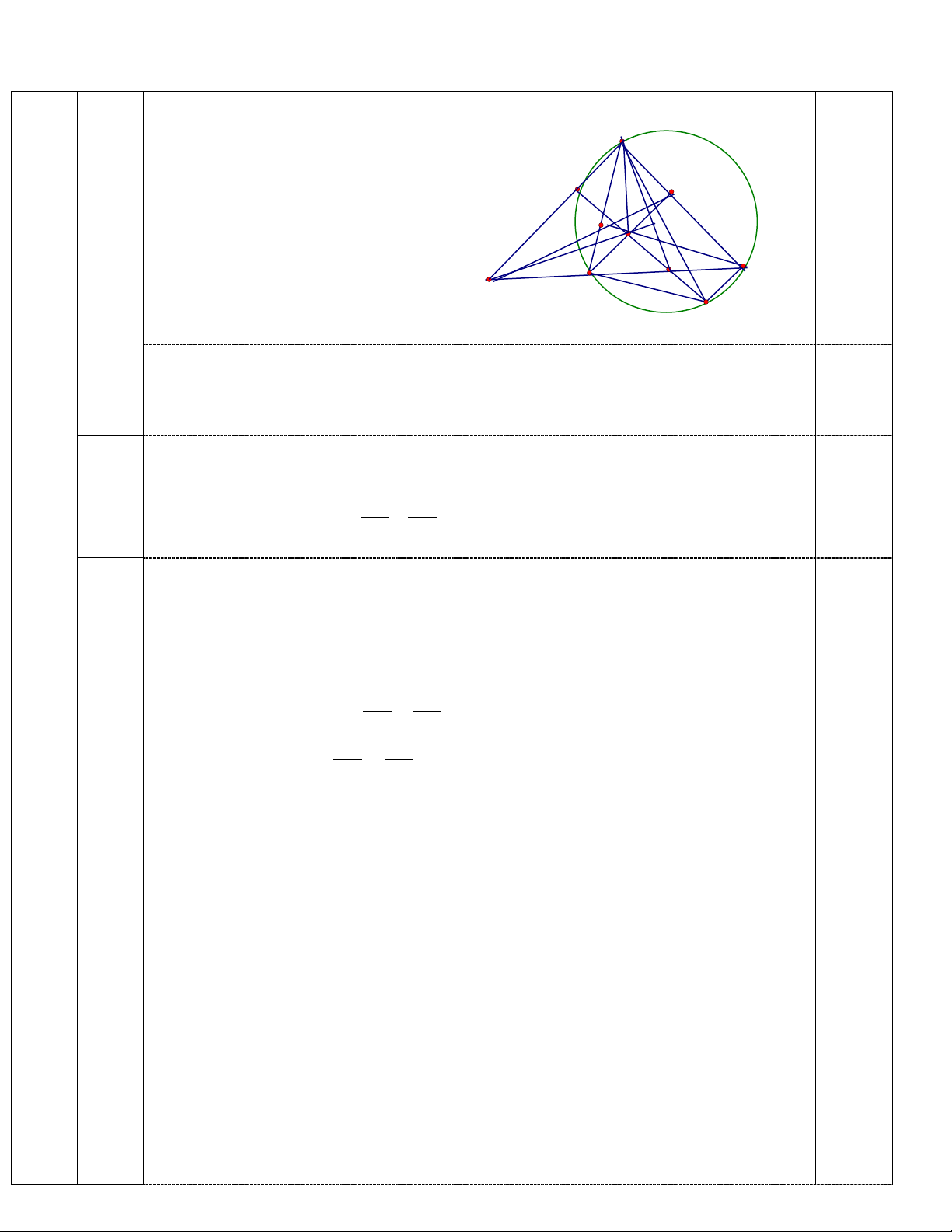
− 2 thỏa mãn yêu cầu đề bài. 0,25 4 (3,0đ) A K D E H M C B F N 1
(1.0đ) 1) Ta có BD ⊥ AC; CE ⊥ AB (GT)⇒  BDC =  0 BEC = 90
Hai điểm E, D cùng nhìn BC dưới một góc vuông
=>tứ giác BEDC nội tiế 1,0
2) Vì BEDC nội tiếp =>  FEB =  FCD 2 (1.0đ) Mà  EFB chung 1,0 => ΔFEB FE FC  ΔFCD (g.g) ⇒ = ⇒ F . D FE = FB.FC FB FD 3
3) Gọi giao điểm của FA với đường tròn
(1.0đ) ngoại tiếp tam giác ABC là K.
Ta có tứ giác AKBC nội tiếp =>  FKB =  FCA Lại có  KFB chung FK FC
=> ΔFKB  ΔFCA (g.g) ⇒ = ⇒ FK. FA = FB.FC FB FA ⇒
. FA = FE. FD ⇒ FK = FD FK FE FA Mà 
KFE chung => ΔFKE  ΔFDA (g.g) =>  FKE = 
FDA => tứ giác AKED nội tiếp. Mặt khác  ADH =  0 AEH = 90 ( GT)
=> A, E, D cùng thuộc đường tròn đường kính AH. 1,0
=>K thuộc đường tròn đường kính AH =>  AKH = 900.
Gọi N là giao điểm của HK và đường tròn ngoại tiếp tam giác ABC.
Ta có AN là đường kính ⇒  ABN =  0 ACN = 90
= > NC // BH; BN // CH => BHCN là hình bình hành => HN đi qua trung
điểm M của BC => MH vuông góc với FA.
Vì H là giao điểm hai đường cao BD, CE nên H là trực tâm của tam giác ABC
=> AH vuông góc với FM.
Trong tam giác FAM có hai đường cao AH, MK nên H là trực tâm của tam giác =>FH vuông góc với AM.
Cho các số thực không âm x,y,z thỏa mãn: x2 + y2 + z2 ≤ 3y
Tìm GTNN của biẻu thức: 1 4 8 P = ( x + ) + + 2 1 (y + 2)2 (z + )2 3
Sử dụng bất đẳng thức Cauchy-Schwarz ta có: 0,25 1 1 1  1 1 2  8 + ≥  +  ≥ ( ) 2 2 a b 2  a b  (a + b) * 2
Áp dụng bất đẳng thức (*) ta có: 0,25 Câu 5 1 1 8 8 8 64 0,25 (1đ) P = (x+ ) + + ≥ + ≥ 2 2 1  y  (z + 3)2 2  y  (z + 3)2 2 y  +1  x + + 2   x + + z + 5    2   2   2  2 Mặt khác: + − x + z ≤ 2( 2 2 x + z ) ≤ 2(3 2
y − y ) 2 3y y ≤ 2 64 64 P ≥ ≥ ≥1 0,25 2 2  y   1 2  6 + 2y − 8 − (y − 2)2    2   2  
Dấu “=” xảy ra khi x=1;y= 2;z=1 Vậy GTNN của P bằng 1
TRƯỜNG THCS LÊ LỢI
KỲ THI THỬ VÀO LỚP 10 THPT
Năm học: 2023 – 2024 Đề B Môn thi: Toán
Thời gian làm bài: 120 phút không kể thời gian giao đề    3 y + y 
Câu 1 (2,0 điểm). Q = 3+   2 : −      
y −1  y + y − 2 y + 2  1. Rút gọn biểu thức Q
2. Tìm các giá trị của y để 5 y − 2 Q = y Câu 2 (2,0 điểm).
1. Giải hệ phương trình sau: 2x + 3y =11 
x − 6y = −17 2.Cho hàm số: y = mx + n.
Tìm m, n biết đồ thị của hàm số đã cho song song với đường thẳng (d ): y = 2x – 3 1
và đi qua giao điểm T của hai đường thẳng (d ): y = 3x + 2; (d ): y = - 2x - 3. 2 3
Câu 3 (2,0 điểm)
1. Giải phương trình: 3x2 + 2x - 5 = 0
2. Tìm các giá trị của tham số n để phương trình 2 x − ( 2 n − ) 1 2
x + n = 0 có hai nghiệm phân biệt
x ,x thỏa mãn hệ thức (x − x + 6n = x − 2x . 1 2 )2 1 2 1 2 Câu 4: (3,0 điểm)
Cho tam giác MNP nhọn (MN > MP). Đường cao NH, PK cắt nhau ở D. HK cắt NP
tại Q. A là trung điểm của NP. Chứng minh rằng:
1) Tứ giác NKHP là tứ giác nội tiếp. 2) QK . QH = QP . QN. 3) QD vuông góc với AM.
Câu 5: (1,0 điểm ) Cho các số thực không âm a,b,c thỏa mãn: a2 + b2 + c2 ≤ b 3
Tìm GTNN của biẻu thức: 1 4 8 P = ( a + ) + + 2 1
(b + 2)2 (c + 3)2
.............................................................Hết............................................................ HƯỚNG DẪN CHẤM ĐỀ B Câu Ý
Lời giải (vắn tắt) Điểm 1 1 (2,0đ)
(1,0đ) a) ĐKXĐ: y ≥ ,0 y ≠ 1 1 0.25 (2,0đ)    3 y + y  Q = 3 +   2 : −      
y −1  y + y − 2 y + 2   ( 3 y − ) 1 3   y + 2 y  Q =  +  :  −    y −1 y −1 
  ( y + 2)( y − ) 1 y + 2 
 3 y − 3 + 3  y + 2 y( y − ) 1  Q =   :  −   0.25  y −1  
  ( y + 2)( y − )
1 ( y + 2)( y − ) 1 
 3 y   y + 2 − y + y  Q =   :    0.25  y −1 
  ( y + 2)( y − ) 1   3 y   2 + y  Q =   :     y −1 
  ( y + 2)( y − ) 1 
3 y ( y + 2)( y − ) 1 Q = ⋅ = 3 y y −1 2 + y Vậy với y ≥ ,
0 y ≠ 1 thì Q=3 y 0,25 2 5 y − 2 5 y − 2 (1,0đ) Q = ⇔ 3 y =
⇒ 3y − 5 y + 2 = 0 ⇔ ( y − ) 1 (3 y − 2)= 0 0,25 y y ( y ( 1 KTM ) y 1 0 y 1 y − ) 1 (3 y − 2)  =  − =  =  = 0 ⇔  ⇔  ⇔  4 3 y − 2 = 0 3 y = 2 y = 0.5   (tm)  9 − Vậy 4 5 y 2 y = Q = 9 thì y 0,25 2 1 (2,0đ) (1,0đ) 2x + 3y = 11 4x + 6y = 22 5x = 5 x = 1 x = 1 0,75  ⇔  ⇔  ⇔  ⇔ 
x − 6y = −17
x − 6y = −17 2x + 3y = 11 2 1 . + 3y = 9 y = 3
Vậy hệ phương trình có một nghiệm duy nhất (x;y)=(1;3) 0,25 2
Vì đồ thị hàm số y = mx +n song song với đường thẳng
(1,0đ) (d ): y = 2x – 3 Nên m= 2; n ≠ 3 − 1
Vì T là giao điểm của hai đường thẳng (d ): y = 3x + 2; 2 ( 0,5
d ): y = - 2x - 3 nên tọa độ của điểm T là nghiệm của hệ 3  y = 3x + 2 x = 1 − phương trình  ⇔  y 2x 3  = − −  y = 1 − => T( -1 ; -1) 0,25
Do đồ thị hàm số đã cho đi qua T nên -1 = - 2 + n => n = 1 thỏa mãn n ≠ 3 −
Vậy m = 2, n = 1 thỏa mãn bài toán 0,25 1 1) 3 2
x + 2x − 5 = 0 3
(1,0đ) Vì a=3;b=2;c=-5 nên a+b+c=3+2+(-5)=0 1,0 (2,0đ) − 5
Vậy phương trình có hai nghiệm phân biệt x = x = 1 ; 1 2 3 2 2 2 x − 2(n −1)x + n = 0 (1,0đ) Ta có: ∆ = −  ( − ) 2 2 ' n 1  − n = − + − = −  2 2 n 2n 1 n 1 2n 0,25
Phương trình có hai nghiệm phân biệt x ,x 1 2 1
⇔ ∆' > 0 ⇔ 1− 2n > 0 ⇔ n < 2 x + x = 2 n −1 1 2 ( ) Theo vi-ét ta có:  2 x x =  n 0,25 1 2 Theo đề bài ta có:
(x − x )2 + 6n = x − 2x ⇔ (x + x − 4x x + 6n = x − 2x 1 2 )2 1 2 1 2 1 2 1 2 ⇔ 4(n − )2 2
1 − 4n + 6n = x − 2x ⇔ 2n − + 4 = x − 2x 1 2 1 2
Khi đó kết hợp với x + x = 2 n −1 ta có hệ pt: 1 2 ( )  4  4 x = n − 2 x = n − 2  x + x = 2 m −1  3x = 4n − 6   1 2 ( ) 2 2  3  3 2  ⇔  ⇔  ⇔  x − 2x = 2m − + 4 x + x = 2n − 2 4 2 1 2 1 2 x 2n 2 n 2  = − − + x = n 0,25 1 1  3  3  4 x = n − 2  2 Thay  3  vào 2 x x = n ta được: 2 1 2  x = n 1  3  4  2 1 − 4  1 4   n = 0 2 2 n − 2
. n = n ⇔ n − n = 0 ⇔ −n n + =  0 ⇔  (tm)  3  3 9 3  9 3   n = 12 − Vậy n = 0;n = 1
− 2 thỏamãn yêu cầu đề bài. 0,25 4 (3,0đ) M L K H D P N A Q G 1
1) Ta có PK ⊥ MN ; NH ⊥ MP (GT)⇒  PKN =  0 PHN = 90 1,0
(1.0đ) Hai điểm K, H cùng nhìn NP dưới một góc vuông =>tứ giác PHKN nội tiếp
2) Vì PHKN nội tiếp =>  QHP =  QNK 1,0 2 (1,0đ) Mà  HQP chung nên ΔQHP QH QN  ΔQNK (g.g) ⇒ = ⇒ QK.QH = QP.QN QP QK
3) Gọi giao điểm của MQ với đường tròn
ngoại tiếp tam giác MNP là L. 1,0
Ta có tứ giác MLPN nội tiếp =>  QLP =  QNM 3 Lại có  LQP chung (1,0đ) => ΔQLP QL QN  ΔQNM (g.g) ⇒ = ⇒ . QL QM = QP.QN QP QM ⇒
. QK = QL. QM ⇒ QH = QM QH mà  LQH chung QL QK => ΔQLH  ΔQKM (g.g) =>  QLH = 
QKM => tứ giác MLHK nội tiếp. Mặt khác  MKD =  0 MHD = 90 ( GT)
=> H, M, K cùng thuộc đường tròn đường kính MD.
=> L thuộc đường tròn đường kính MD =>  MLD = 900.
Gọi G là giao điểm của LD và đường tròn ngoại tiếp tam giác MNP. Ta có 
MLD = 900 => MG là đường kính ⇒  MNG =  0 MPG = 90
= > ND // PG; GN // PD => PDNG là hình bình hành => GD đi
qua trung điểm A của NP => DA vuông góc với MQ.
Vì D là giao điểm hai đường cao NH, PK nên D là trực tâm của tam giác MNP
=> MD vuông góc với QN.
Trong tam giác MQA có hai đường cao MD, AD nên D là trực tâm của tam giác
=> QD vuông góc với AM. Câu 5
Cho các số thực không âm x,y,z thỏa mãn: 2 2 2
a + b + c ≤ 3b (1đ) 1 4 8 1,0đ
Tìm GTNN của biẻu thức: P = + + (a + )2 1 (b + 2)2 (c +3)2
Sử dụng bất đẳng thức Cauchy-Schwarz ta có: 0,25 2 1 1 1  1 1  8 + ≥ + ≥   * 2 2 2 ( ) x y
2  x y  (x + y)
Áp dụng bất đẳng thức (*) ta có: 0,25 1 1 8 8 8 64 P = + + ≥ + ≥ ( a + )2 2 1  b  (c +3)2 2  b  (c +3)2 2 1  a 2  b   a c 5 + + + + + +  2 2 2        0,25 Mặt khác: ( ) ( ) 2 2 2 2 2 3 2 2 3 b b a c a c b b + − + ≤ + ≤ − ≤ 2 64 64 P ≥ ≥ ≥1 2 2 2  b   1  6 + 2b −  8 − (b − 2)2 2  2    
Dấu “=” xảy ra khi a=1;b= 2;c=1 Vậy GTNN của P bằng 1 0,25