Đề thi thử Toán vào lớp 10 năm 2023 – 2024 trường THCS Nguyễn Trãi – Hà Tĩnh

ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT
TRƯỜNG THCS NGUYỄN TRÃI NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn thi: TOÁN 9
Thời gian làm bài: 90 phút Mã đề 01
Câu 1.(2 điểm) Rút gọn các biểu thức: a) A  32  50 .  1 1   2  b) B    .1 
 với x  0; x  4 .  x  2 x  2   x 
Câu 2.(1 điểm) Trong mặt phẳng toạ độ Oxy, cho biết đường thẳng (d): y  x  m  2
song song với đường thẳng (d’):   2 y
m  2 x  3 . Hãy tìm giá trị của m.
Câu 3.(2 điểm) x  y  3
a) Giải hệ phương trình:  .
2x  3y  4 b) Cho phương trình: 2 2
x  2mx  m  3m  6  0(m là tham số). Tìm m để phương trình
có hai nghiệm phân biệt x , x 2 x x  x
 x  7 x  x 12 1 2 thỏa mãn . 1  1 2  2  1 2
Câu 4.(1 điểm) Quãng đường từ Nghi Xuân (tỉnh Hà Tĩnh) đến Thanh Hoá có chiều dài
khoảng 150 km. Một người đi ô tô từ Nghi Xuân đến Thanh Hoá, nghỉ tại đó 3 giờ rồi trở
về Nghi Xuân hết tất cả 9 giờ 45 phút. Tính vận tốc của ô tô lúc đi, biết rằng vận tốc lúc đi
lớn hơn vận tốc lúc về là 10 km/h.
Câu 5.(1 điểm) Cho tam giác ABC vuông tại A, đường cao AH, đường phân giác AD(H, D
thuộc BC) có AB = 3 cm, AC = 4 cm. Tính độ dài AH và diện tích tam giác ABD.
Câu 6.(2 điểm) Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Kẻ AH vuông
góc với BC tại H và BE vuông góc với đường kính AD tại E.
a) Chứng minh tứ giác AEHB nội tiếp.
b) Gọi M là trung điểm của BC. Chứng minh HE vuông góc với AC và tam giác MHE cân.
Câu 7.(1 điểm) Cho hai số thực a, b thỏa mãn 2 2
a  b  2 . Tìm giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức Q  5a  b  2ab 12 .
- - - - - HẾT - - - - -
Lưu ý: - Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên: .................................................................................. Số báo danh: ........................
ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT
TRƯỜNG THCS NGUYỄN TRÃI NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn thi: TOÁN 9
Thời gian làm bài: 90 phút Mã đề 02
Câu 1.(2 điểm) Rút gọn các biểu thức: a) A  18  50 .  1 1   3  b) B    .1 
với x  0; x  9 .  x  3 x  3   x 
Câu 2.(1 điểm) Trong mặt phẳng toạ độ Oxy, cho biết đường thẳng (d): y  x  m  4
song song với đường thẳng (d’):   2 y
m  2 x  3 . Hãy tìm giá trị của m.
Câu 3.(2 điểm) x  y  4
a) Giải hệ phương trình:  .
2x  3y  7 b) Cho phương trình: 2 2
x  2mx  m  2m  4  0 (m là tham số). Tìm m để phương trình
có hai nghiệm phân biệt x , x 2 x x  x
 x  7 x  x 19 1 2 thỏa mãn . 1  1 2  2  1 2
Câu 4.(1 điểm) Quãng đường từ Nghi Xuân (tỉnh Hà Tĩnh) đến Thanh Hoá có chiều dài
khoảng 150 km. Một người đi ô tô từ Nghi Xuân đến Thanh Hoá, nghỉ tại đó 3 giờ rồi trở
về Nghi Xuân hết tất cả 9 giờ 45 phút. Tính vận tốc của ô tô lúc về, biết rằng vận tốc lúc đi
lớn hơn vận tốc lúc về là 10 km/h.
Câu 5.(1 điểm) Cho tam giác ABC vuông tại A, đường cao AH, đường phân giác AD (H, D
thuộc BC) có AB = 6 cm, AC = 8 cm. Tính độ dài AH và diện tích tam giác ABD.
Câu 6.(2 điểm) Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Kẻ AI vuông
góc với BC tại I và BE vuông góc với đường kính AD tại E.
a) Chứng minh tứ giác ABIE nội tiếp.
b) Gọi K là trung điểm của BC. Chứng minh IE vuông góc với AC và tam giác KIE cân.
Câu 7.(1 điểm) Cho hai số thực x, y thỏa mãn 2 2
x  y  2 . Tìm giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức Q  5x  y  2xy 12.
- - - - - HẾT - - - - -
Lưu ý: - Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên: .................................................................................. Số báo danh: ........................
HƯỚNG DẪN CHẤM MÔN TOÁN MÃ ĐỀ 01 Câu Nội dung Điểm Câu 1 2 2 1 đ
A  32  50  4 .2  5 .2  4 2  5 2  9 2 (2 điểm)  1 1  x  2
x  2  x  2 x   2 B   .  .  x  2 x  2  x
 x 2 x 2 x 2 x x   2 2  1 đ
x 2 x 2 .    x x  2 Câu 2 2
Câu 2.(d): y  x  m  2 song song với (d’): y  m  2 x  3 (1 1,0 đ điểm) 2 2 a   a '  1   m  2 m 1 m  1          m  1  b  b' m  2  3 m 1 m 1 Câu 3 x  y  3 x 1 1,0 đ
a) (1 điểm)   ...   .
 x  y   y   (2 2 3 4 2 điểm) b) Phương trình 2 2
x  2mx  m  3m  6  0có hai nghiệm x , x   '  0 1 2 0.25đ 2 2
 m  m  3m  6  0  3m  6  0  m  2 (*)
x  x  2m
Áp dụng hệ thức Vi – et ta có: 1 2  . 2
x x  m  3m  6  1 2 0.25đ Theo đề bài ta có:
x  x  x  2
 x  7x  x  2 2
12  x  x  x x  7 x  x 12 1 1 2 2 1 2 1 2 1 2  1 2
 x  x 2  3x x  7x  x  2
12  0  4m  3 2
m  3m  6  7.2m  12  0 1 2 1 2 1 2  2 2
 4m  3m  9m 18 14m 12  0 0.25đ 2 2
 m  5m  6  0  m  6m  m  6  0
 mm    m     m  m   m  6( * tm ) 6 6 0 6 1  0   . Vậy m  6 m  1  (k * tm ) 0.25đ Câu 4
Gọi vận tốc lúc về là x (km/h). ĐK: x > 0. (1 150 150 3 150 150 27 50 50 9 100x  500 9            0.5đ điể 3 9 m) x 10 x 4 x 10 x 4 x 10 x 4 x x 10 4
Đưa được PT về dạng: 2 9x  310x  2000  0 0.25đ
Giải phương trình được x = 40 (loại giá trị 50 
< 0). Vậy vận tốc đi là 40 + 10 = 50 km/h 0.25đ 9
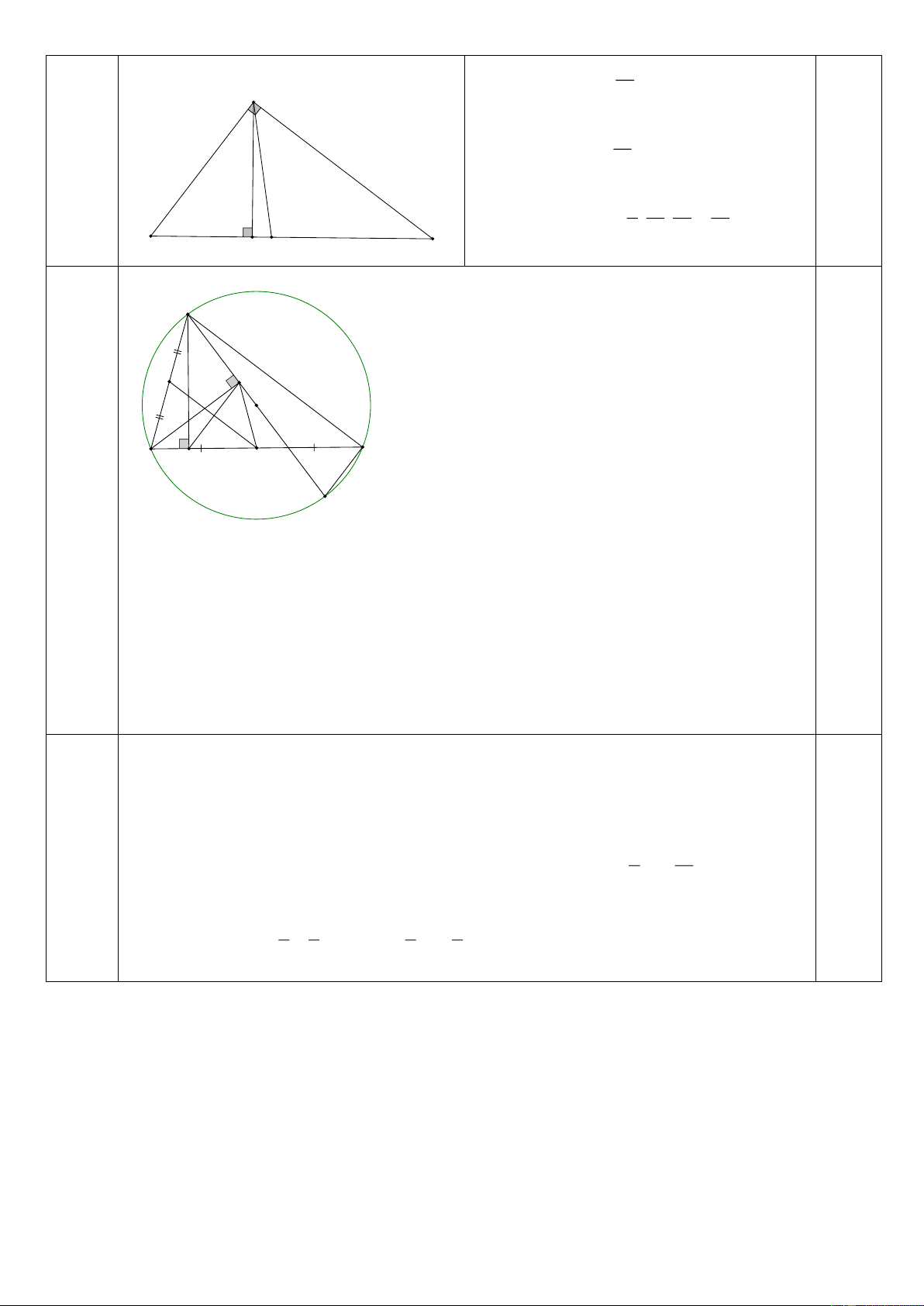
(Lưu ý HS có thể gọi vận tốc lúc đi) 12 Câu 5 - Tính được AH = (cm) 0.5đ A 5 (1 0.25đ điể 15 m) - Tính được BD  (cm) 7 1 15 12 18 0.25đ - Tính được: 2 S  . .  (cm ) ABD 2 7 5 7 B H C D Câu 6 A (2 (HV điểm) N E 0,25đ) O B C H M D 0.75đ
a) Chứng minh được tứ giác AEHB nội tiếp 0,25đ
b) - Chứng minh HE//CD( HED  ABC  ADC ).
- Chứng minh HE vuông góc với AC. 0,25 đ
- Gọi N là trung điểm của AB, chứng minh được NH = NE (= AB:2) và MN vuông
góc với HE suy ra MN là đường trung trực của HE
Suy ra MH = ME => tam giác MHE cân tại M 0.5đ Câu 7    2 2 2 2 2 0.25đ Ta co : a b  2(a  b )  4  2
  a  b  2; 2ab  a  b  2  Q  0. (1
 MaxQ  0 a  b 1. 0.25đ điểm) 2   Đặ 5 81 t 2 2 a  b  t  2
  t  2  2ab  t  2  Q  5t  t 14  t     .  0.25đ 2  4 2 5 1  5  1 Mà 2
  t  2  t    0  t 
  Q  20  Min Q  20  a  b  1.   0.25đ 2 2  2  4
HƯỚNG DẪN CHẤM MÔN TOÁN MÃ ĐỀ 02 Câu Nội dung Điểm Câu 1 2 2 1 đ
A  18  50  3 .2  5 .2  3 2  5 2  8 2 (2 điểm)  1 1  x  3
x  3  x  3 x   3 B   .  .  x  3 x  3  x
 x 3 x 3 x 2 x x   3 2  1 đ
x 3 x 3 .    x x  3 Câu 2 2
Câu 2.(d): y  x  m  4 song song với (d’): y  m  2 x  3 (1 điểm) 1,0 đ 2 2 a   a '  1   m  2 m 1 m  1          m 1 b  b' m  4  3 m  1  m  1  Câu 3 x  y  4 x 1 1,0 đ
a) (1 điểm)   ...   . (2 điể
 x  y   y   m) 2 3 7 3 b) Phương trình 2 2
x  2mx  m  2m  4  0 có hai nghiệm x , x   '  0 1 2 0.25đ 2 2
 m  m  2m  4  0  2m  4  0  m  2(*)
x  x  2m
Áp dụng hệ thức Vi – et ta có: 1 2  . 2
x x  m  2m  4  1 2 0.25đ Theo đề bài ta có:
x  x  x  2
 x  7x  x  2 2
12  x  x  x x  7 x  x 19 1 1 2 2 1 2 1 2 1 2  1 2
 x  x 2  3x x  7x  x  2
19  0  4m  3 2
m  2m  4  7.2m  19  0 1 2 1 2 1 2  2 2
 4m  3m  6m 12 14m 19  0 0.25đ 2 2
 m  8m  7  0  m  7m  m  7  0
 mm    m     m  m   m  7(tm) 7 7 0 7 1  0   . Vậy m  7 m 1(ktm) 0.25đ Câu 4
Gọi vận tốc lúc về là x (km/h). ĐK: x > 0. (1 điểm) 150 150 3 150 150 27 50 50 9 100x  500 9  0.5đ 3   9         x 10 x 4 x 10 x 4 x 10 x 4 x x 10 4
Đưa được PT về dạng: 2 9x  310x  2000  0 0.25đ
Giải phương trình được x = 40 (loại giá trị 50 
<0). Vậy vận tốc về là 40 km/h. 0.25đ 9
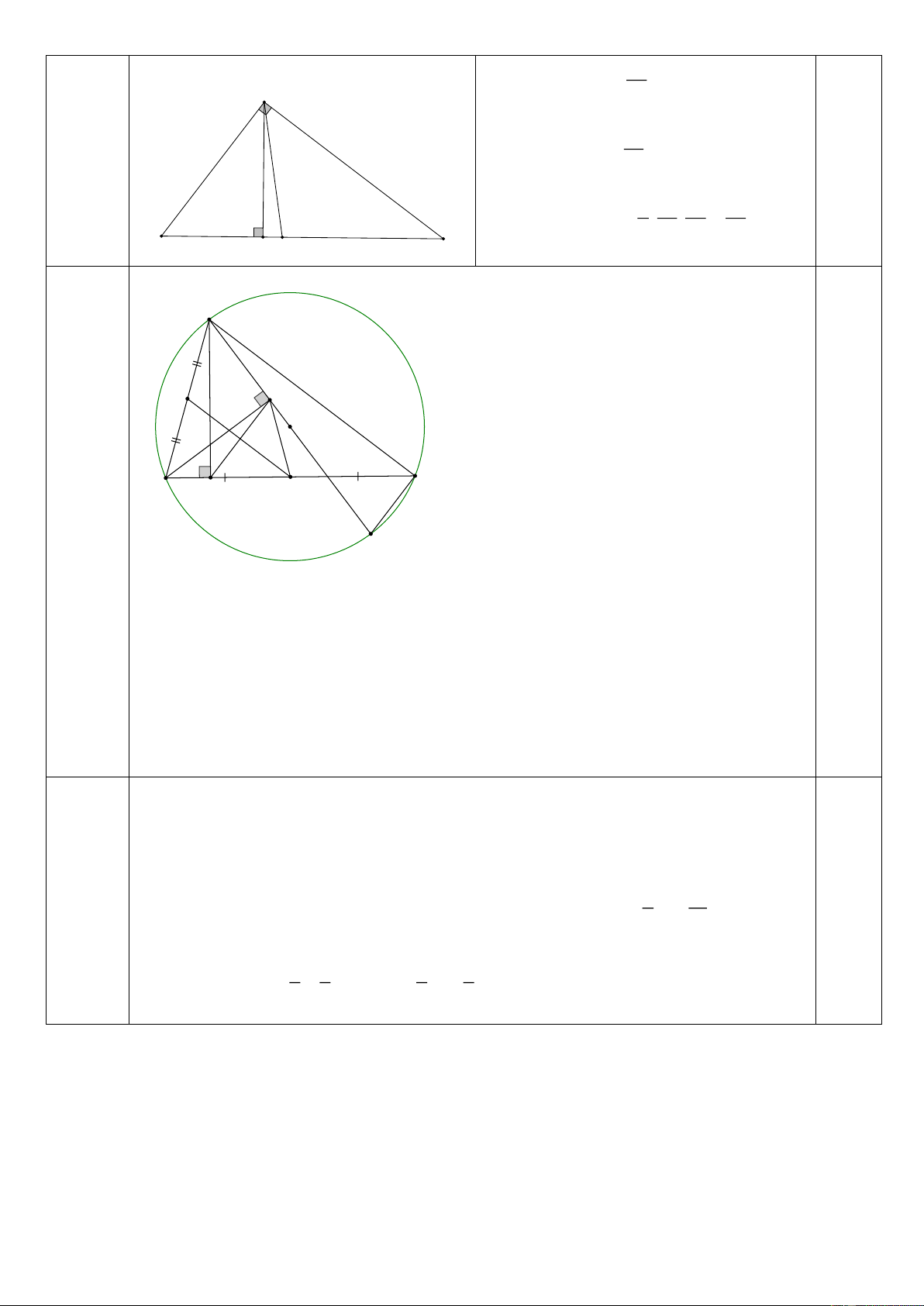
(Lưu ý HS có thể gọi vận tốc lúc đi) 24  Câu 5 - Tính được AH = (cm) 0.5đ A 5 (1 điể m) 0.25đ 30 - Tính được BD  (cm) 7 1 30 24 72 0.25đ - Tính được: 2 S  . .  (cm ) ABD 2 7 5 7 B H C D Câu 6 A (2 điểm) (HV 0,25đ) N E O B C I K D
c) Chứng minh được tứ giác ABIE nội tiếp 0.75đ 0,25đ
d) - Chứng minh IE//CD ( IED  ABC  ADC ).
- Chứng minh HE vuông góc với AC. 0,25 đ
- Gọi N là trung điểm của AB, chứng minh được NI = NE (= AB:2) và KN vuông
góc với IE suy ra KN là đường trung trực của IE
Suy ra KI = KE => tam giác KIE cân tại K 0.5đ Câu 7    2 2 2 2 2 0.25đ Ta co : x y  2(x  y )  4  2
  x  y  2; 2xy  x  y  2  Q  0.
(1 điểm)  MaxQ  0  x  y  1. 0.25đ 2   Đặ 5 81 t 2 2 x  y  t  2
  t  2  2xy  t  2  Q  5t  t 14  t     .  0.25đ 2  4 2 5 1  5  1 Mà 2
  t  2  t    0  t 
  Q  20  Min Q  20  x  y  1.   0.25đ 2 2  2  4