Đề thi thử Toán vào lớp 10 năm 2024 – 2025 phòng GD&ĐT Bình Giang – Hải Dương

UBND HUYỆN BÌNH GIANG
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024 - 2025 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề bài gồm 01 trang) MÃ ĐỀ 01
Câu 1 (2,0 điểm): Giải phương trình và hệ phương trình sau:
x + y = 3 5
1) 12 − 3x = x + 2 2) 
2x − 3y = 5 Câu 2 (2,0 điểm):  + − +  1) Rút gọn biểu thức: 2
a a a 2a 4 a  4 P   : 3  = − −
, với a ≥ 0,a ≠ 4.  a 2 a a 8   a 2  − + + 
2) Tìm số nguyên m để hai đường thẳng sau: y = −x + 3m và y = 0,5x +1,5 cắt nhau tại
một điểm có tọa độ ( ; x y) sao cho: 2 x + xy = 30 . Câu 3 (2,0 điểm):
1) Hai tỉnh A và B cách nhau 260(km) . Một ô tô dự định đi từ A đến B với thời gian đã
định. Sau khi đi được 80(km) với vận tốc dự định, người lái xe tăng vận tốc thêm 10(km / h), do
đó ô tô đã đến B sớm hơn dự định 54 phút. Tính vận tốc dự định của ô tô. 2) Cho phương trình: 2 x − (m − ) 2 2
1 x + m − 2m − 3 = 0 (với m là tham số). Tìm m để
phương trình đã cho có hai nghiệm x ; x x + 4 = x 1 2 thỏa mãn: 1 2 Câu 4 (3,0 điểm):
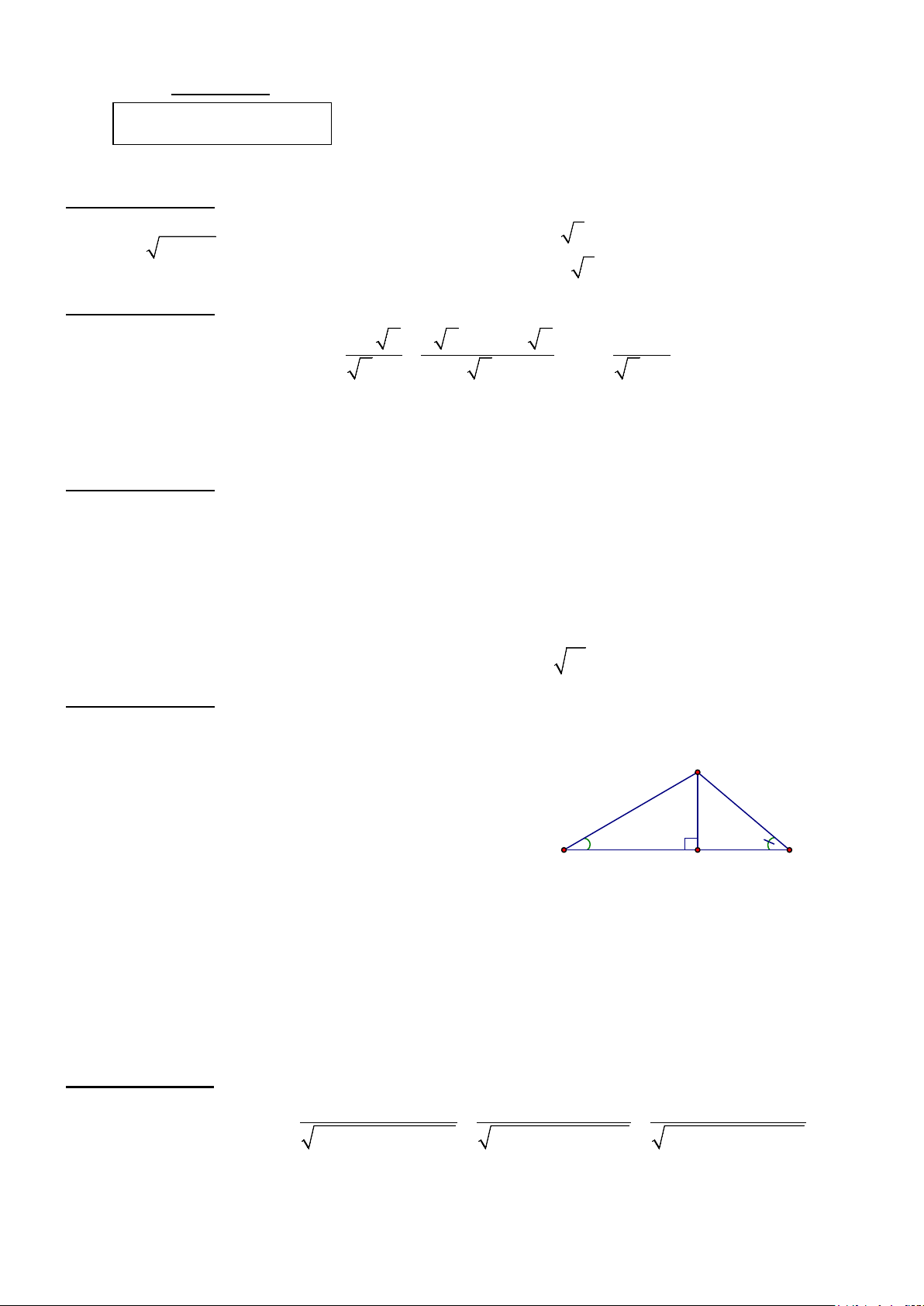
1) Điểm hạ cánh của một máy bay trực thăng
ở giữa hai người quan sát A và B. Biết máy bay M ( áy bay) C
cách mặt đất là 125(m), góc nhìn thấy máy bay tạo
với mặt đất tại vị trí A là 0 40 và tại vị trí B là 0 30 . 400 300
Hãy tìm khoảng cách giữa hai người quan sát A và B H A
B (kết quả làm tròn đến hàng đơn vị).
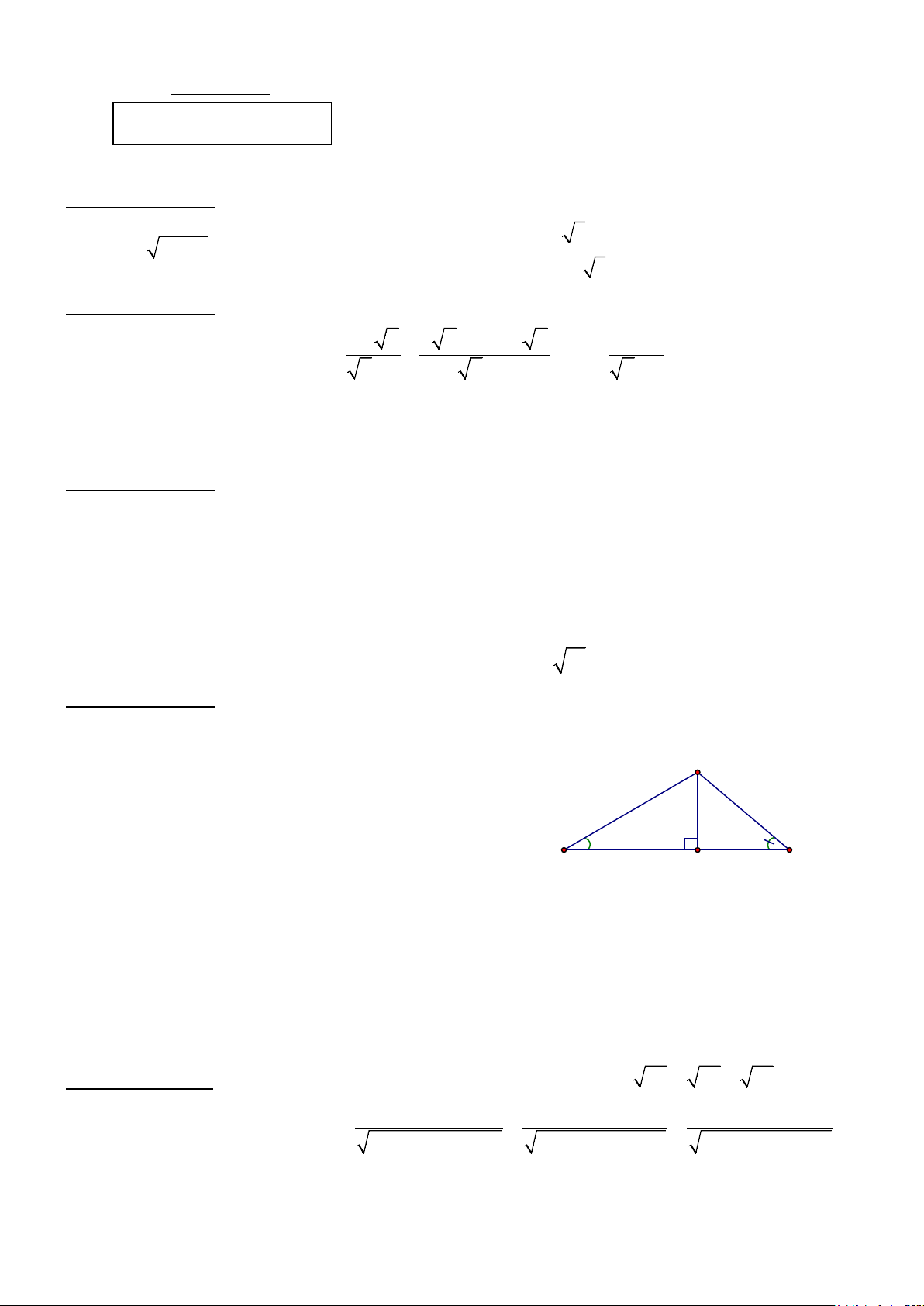
2) Cho tam giác ABC có ba góc nhọn, AB < AC nội tiếp đường tròn (O). Ba đường cao AD,
BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K (K ≠ A). Tiếp tuyến tại C của đường tròn
(O) cắt đường thẳng FD tại M. AM cắt đường tròn (O) tại I (I ≠ A), MD cắt BI tại N.
a) Chứng minh: Tứ giác ACDF nội tiếp và tam giác CMD cân. b) Chứng minh: 2
MD = MI.MA và ba điểm C, N, K thẳng hàng.
Câu 5 (1,0 điểm): Cho a, b, c là các số thực dương thay đổi thỏa mãn: 2 2 2
a + b + c = 3. Tìm giá trị
lớn nhất của biểu thức: ab bc ca M = + + 2 2 2 2 2 2
5a +10ab +10b
5b +10bc +10c
5c +10ca +10a
---------- HẾT ---------
Họ và tên thí sinh: ........................................... Số báo danh: ......................
Giám thị 1: ...................................................... Giám thị 2: ........................................ UBND HUYỆN BÌNH GIANG
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024 - 2025 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề bài gồm 01 trang) MÃ ĐỀ 02
Câu 1 (2,0 điểm): Giải phương trình và hệ phương trình sau:
x + y = 3 3
1) 31− x = x −1 2)  3
 x − 2y = 4 3 Câu 2 (2,0 điểm):  + − +  1) Rút gọn biểu thức: 3
x x x 3x 9 x  6 P   : 3  = − −
, với x ≥ 0, x ≠ 9 .  x 3 x x 27   x 3  − + + 
2) Tìm số dương m để hai đường thẳng sau: y = 3x − m và y = 2x + 5 cắt nhau tại một điểm có tọa độ ( ; x y) sao cho: 2 x − xy = 66 − . Câu 3 (2,0 điểm):
1) Hai tỉnh A và B cách nhau 260(km) . Một ô tô dự định đi từ A đến B với thời gian đã
định. Sau khi đi được 100(km) với vận tốc dự định, người lái xe giảm bớt vận tốc đi 10(km / h),
do đó ô tô đã đến B muộn hơn dự định 48 phút. Tính vận tốc dự định của ô tô. 2) Cho phương trình: 2 x − (m − ) 2 2
2 x + m − 4m − 5 = 0 (với m là tham số). Tìm m để
phương trình đã cho có hai nghiệm x ; x x + 6 = x 1 2 thỏa mãn: 1 2 Câu 4 (3,0 điểm):
1) Điểm hạ cánh của một máy bay trực thăng
ở giữa hai người quan sát A và B cách nhau M ( áy bay) C
300(m) . Góc nhìn thấy máy bay tạo với mặt đất tại vị trí A là 0 40 và tại vị trí B là 0 30 . Hãy tìm chiều 400 300
cao CH của máy bay so với mặt đất (kết quả làm B H A
tròn đến hàng đơn vị).
2) Cho tam giác MNP có ba góc nhọn, MN < MP nội tiếp đường tròn (O). Ba đường cao
MD, NE, PF cắt nhau tại H. Tia MD cắt đường tròn (O) ở I (I ≠ M). Tiếp tuyến tại P của đường
tròn (O) cắt đường thẳng FD tại K. MK cắt đường tròn (O) tại T (T ≠ M), KD cắt NT tại R.
a) Chứng minh: Tứ giác MPDF nội tiếp và tam giác PKD cân. b) Chứng minh: 2
KD = KT.KM và ba điểm P, R, I thẳng hàng.
Câu 5 (1,0 điểm): Cho a, b, c là các số thực dương thay đổi thỏa mãn: ab + ac + bc =15. Tìm 2 2 2
giá trị nhỏ nhất của biểu thức: M = a b c + + 2 2 2 2 2 2
3a + 8b +14ab
3b + 8c +14bc
3c + 8a +14ca
---------- HẾT ---------
Họ và tên thí sinh: ........................................... Số báo danh: ......................
Giám thị 1: ...................................................... Giám thị 2: ........................................ UBND HUYỆN BÌNH GIANG
HƯỚNG DẪN CHẤM THI THỬ VÀO LỚP 10 THPT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC: 2024 - 2025. MÔN: TOÁN
(Hướng dẫn chấm gồm 03 trang) MÃ ĐỀ 01 Câu Ý Nội dung Điểm
12 −3x = x + 2 (1). ĐK: 2 − ≤ x ≤ 4 0,25
Bình phương 2 vế của (1) ta được:
( 12−3x)2 =(x+2)2 2 2 1)
⇔ 12 − 3x = x + 4x + 4 ⇔ x + 7x −8 = 0 0,25
Vì a + b + c = 1 + 7 + (-8) = 0 nên x =1 c 1 ; x = = 8 − (loại). 2 0,25 a
Vậy phương trình (1) có nghiệm x =1 0,25 x + y =
x = 3 5 − y x = 3 5 − y 1 Ta có: 3 5   ⇔  ⇔  0,25
2x − 3y = 5
2x − 3y = 5 2
 (3 5 − y) − 3y =  5
x = 3 5 − y
x = 3 5 − y
x = 3 5 − y ⇔  ⇔  ⇔  0,25 2)
6 5 − 2y − 3y = 5  5 − y = 5 − 5 y = 5 x = 3 5 − 5 x = 2 5 ⇔  ⇔  0,25 y = 5 y = 5
Vậy nghiệm của hệ phương trình là: (x, y) = (2 5; 5) 0,25
 2 + a a a − 2a + 4 a   4 P   :   3  = − −
, với a ≥ 0,a ≠ 4 .  a − 2 a a + 8   a + 2   a 0,25 a (a−2 a + + 4 2 )  3 a +6−4 P =  −   a − 
( a +2)(a−2 a +4) : 2  a + 2  1)  2 + a a  a + 2 P =  − .  a 2 a 2  − + 3 a + 0,25   2
a + 4 a + 4 − a + 2 a a + 2 6 a + 4 a + 2 P = ( =
a − 2)( a + 2) . a +
( a −2)( a +2). 3 2 3 a + 2 0,25 2 2 P = . Vậy 2 P =
, với a ≥ 0,a ≠ 4 . 0,25 a − 2 a − 2
Đồ thị các hàm số y = −x + 3m và y = 0,5x +1,5 cắt nhau tại điểm có tọa độ (x;
y) nên (x; y) là nghiệm của hệ:
y = −x + 3m  x + = −x + m x = m − 0,25  0,5 1,5 3 2 1 ⇔  ⇔  y = 0,5x +1,5
y = −x + 3m y = m +1 2 2 + = ⇒ − + − + =
2) Theo bài ra: x xy 30
(2m )1 (2m )1(m )1 30 0,25 2
⇔ 2m − m −10 = 0 ⇔ (  = − m + )( m − ) m 2 2 2 5 = 0 ⇔  0,25 m = 2,5
Mà m là số nguyên, nên m = 2
− (TM); m = 2,5 (loại) 0,25
Vậy m = -2 thoả mãn yêu cầu đề bài.
Gọi vận tốc dự định của ô tô là x (km/h) (đk: x > 0) 3
1) Thời gian ô tô dự định đi từ A đến B là: 260 (giờ) 0,25 x
Thời gian ô tô đi hết 80 km đầu là: 80 (giờ) x
Quãng đường còn lại dài là 260 – 80 = 180 (km)
Vận tốc của ô tô đi trên đoạn đường còn lại là x +10 (km/h) 0,25
Thời gian ô tô đi hết đoạn đường còn lại là: 180 (giờ) x +10 Đổi 54 phút = 9 (giờ) 10 0,25
Theo bài ra ta có pt: 260  80 180  9 − + = x   x x 10  +  10 180 180 9 1 1 1 ⇔ − = ⇔ − = x x +10 10 x x +10 200
⇒ 200(x +10) − 200x = x(x +10) 2
⇔ x +10x − 2000 = 0 0,25 ⇔ (  = x − )(x + ) x 40 (tm) 40 50 = 0 ⇔ x = 50 − (ktm)
Vậy vận tốc dự định của ô tô là 40 km/h.
Xét phương trình: x2 – 2(m - 1)x + m2 - 2m - 3 = 0
Ta có: ∆ = (m − )2 −( 2 ' 1
m − 2m − 3) = 4 > 0 nên pt luôn có hai nghiệm phân biệt 0,25 x ; x 1 2 với mọi m.
Tính được hai nghiệm của phương trình là: x = m − 3; x = m +1 0,25
* Trường hợp 1: x = m − 3; x = m +1 1 2
, điều kiện bài toán trở thành: m ≥ 1 −  m ≥ 1 − m = 0 0,25
2) m +1 = m +1 ⇔ ( ⇔  ⇔ (TM)  m +  )2 1 − (m + ) 1 = 0 m  (m )1 0  + = m = 1 −
* Trường hợp 2: x = m +1; x = m − 3, điều kiện bài toán trở thành: 1 2 m ≥ 3  m ≥ 3
m + 5 = m − 3 ⇔ ( ⇔   m + 5 0,25  )2 −(m −3) 2 = 0
m + 9m + 28 = 0 Ta có: Phương trình 2
m + 9m + 28 = 0 vô nghiệm vì: ∆ = - 31< 0
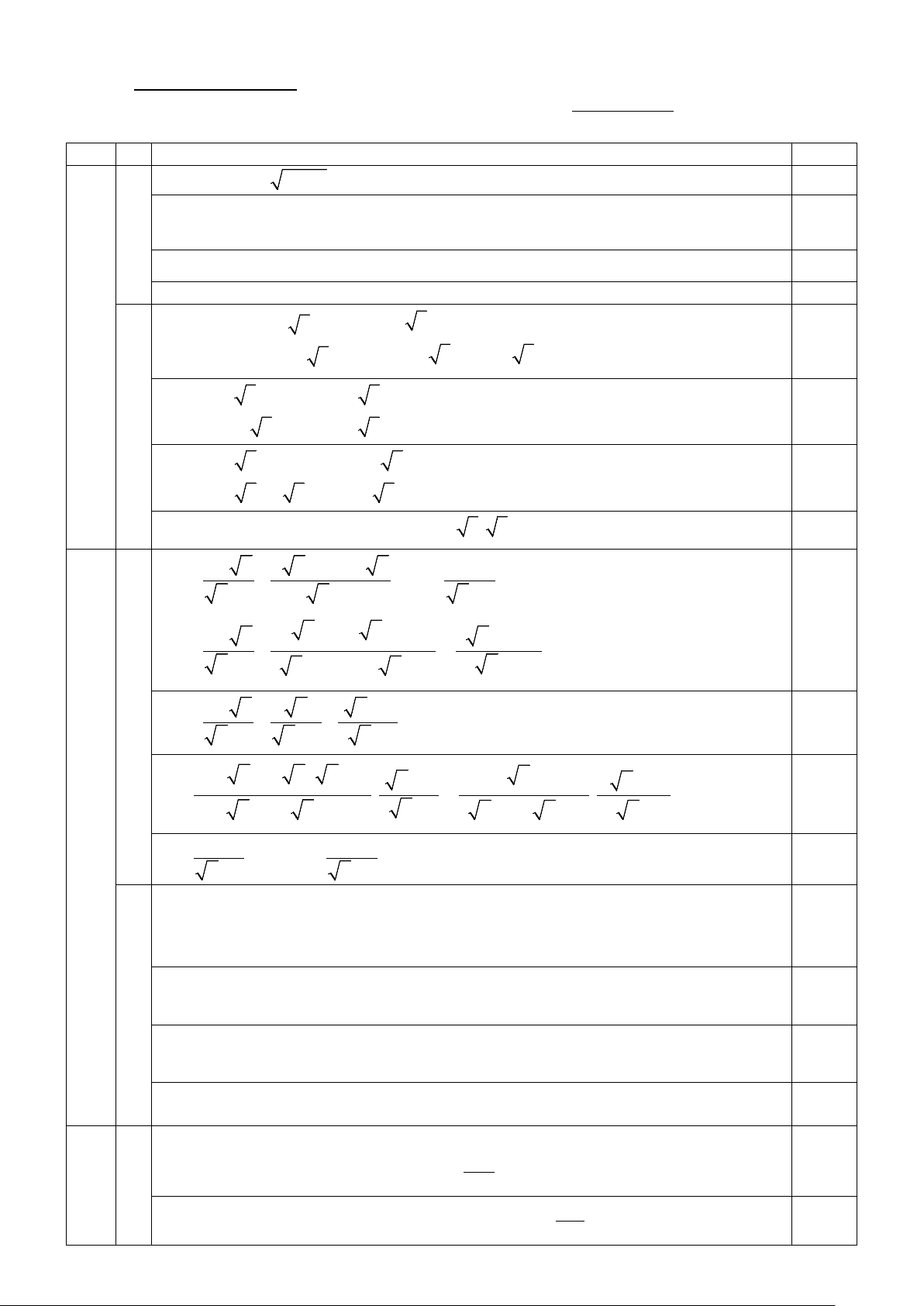
Vậy m = 0; m = -1 là giá trị cần tìm thỏa mãn điều kiện bài toán. C 1 Hình vẽ 300 400 A H B
Vì máy bay cách mặt đất 125m nên CH = 125m 0,25 4
Xét ∆ AHC vuông tại H ta có CH = AH.tan A => AH = CH = 125 0,25 tan A 0 tan 40
Xét ∆ CHB vuông tại H có CH = HB. tanB => BH = CH = 125 0,25 tanB 0 tan 30
AB = AH + HB = 125 + 125 ≈ 365m 0 tan 40 0 tan 30 0,25
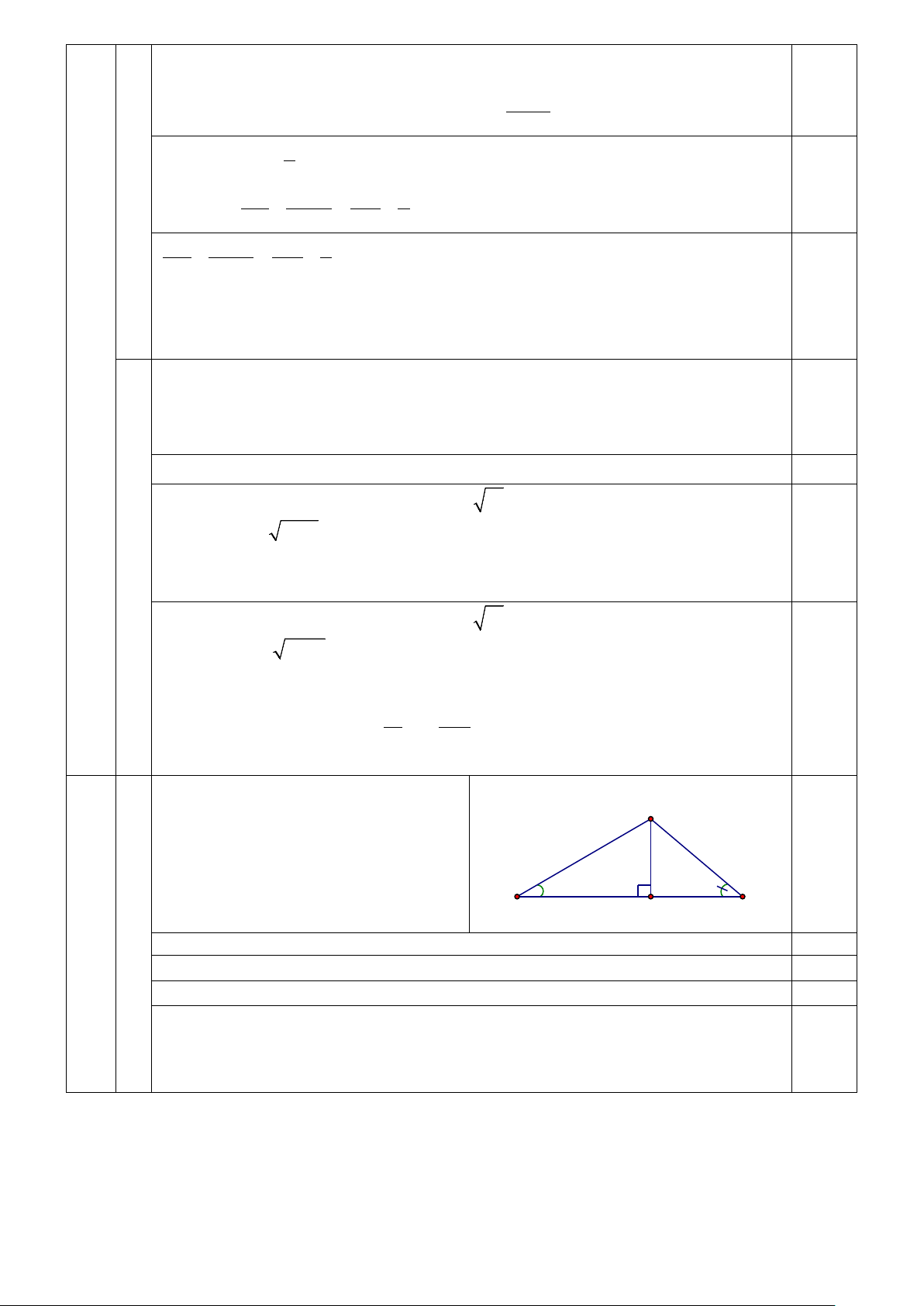
Vậy khoảng cách giữa hai người A và B khoảng 365 (m) A E F O H B D C Hình vẽ K N 0,25 I 2a) M 4
Chứng minh được tứ giác ACDF nội tiếp. 0,25
Vì tứ giác ACDF nội tiếp nên  =  CAB CDM Ta có  = 
CAB MCB (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng 0,25 chắn cung BC) Do đó  = 
MCD CDM ⇒ ∆CMD cân tại M. 0,25
Chứng minh được ∆MIC ∼ ∆MCA (g.g) MI MC ⇒ = ⇒ MC2 = MI.MA. 0,25 MC MA
∆CMD cân tại M => MC = MD => MD2 = MI.MA 0,25 Do MD2 = MI.MA và 
IMD chung ⇒∆MDI ∼ ∆MAD (c.g.c) 0,25 2b) ⇒  =  MDI DAM hay  =  KAI NDI. Mà  =  KAI KCI ⇒  =  KCI NDI (1)
* ∆CMD cân tại M nên  =  =  NDC MCD CAB ⇒  +  0 NIC NDC =180
⇒ tứ giác CIND nội tiếp ⇒  =  NCI NDI (2) 0,25 Từ (1) và (2) ⇒  = 
KCI NCI suy ra hai tia CK và CN trùng nhau.
Suy ra ba điểm C, N, K thẳng hàng. Ta có: 2 2 2 2 2
5a +10ab +10b = (2a + 3b) + (a −b) ≥ (2a + 3b) , dấu “=” có khi a = b Suy ra: 2 2
5a +10ab +10b ≥ 2a + 3b ab ab ⇒ ≤ . 0,25 2 2
5a +10ab +10b 2a + 3b Ta chứng minh: ab 3a + 2b ≤ (*) 2a + 3b 25 Thật vậy: (*) 2
⇔ 25ab ≤ (2a + 3b)(3a + 2b) ⇔ 6(a − b) ≥ 0 (luôn đúng) 0,25
Dấu “=” xảy ra khi a = b. Do đó: ab 3a + 2b ≤ 2 2
5a +10ab +10b 25 5 Tương tự: bc 3b + 2c + ≤ ; ca 3c 2a ≤ 2 2
5b +10bc +10c 25 2 2
5c +10ca +10a 25 0,25
Cộng các BĐT trên ta được:
3a + 2b 3b + 2c 3c + 2a 1 M ≤ + +
= (a + b + c) 25 25 25 5 2 2 2 2
(a + b + c) = a + b + c + (2ab + 2bc + 2ca) Ta có: 2 2 2 2 2 2 2 2 2
≤ a + b + c + (a + b ) + (b + c ) + (c + a ) = 2 2 2
3a + 3b + 3c = 9 . Do đó: a + b + c ≤ 3 . Suy ra 3 M ≤ . 0,25 5
Vậy giá trị lớn nhất của M bằng 3 khi a = b = c = 1. 5
Chú ý: HS làm theo cách khác đúng vẫn cho điểm tối đa UBND HUYỆN BÌNH GIANG
HƯỚNG DẪN CHẤM THI THỬ VÀO LỚP 10 THPT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC: 2024 - 2025. MÔN: TOÁN
(Hướng dẫn chấm gồm 03 trang) MÃ ĐỀ 02 Câu Ý Nội dung Điểm
Phương trình: 31− x = x −1. ĐK: 1≤ x ≤ 31 0,25
Bình phương hai vế, ta được: 1
− x = (x − )2 2 2 31
1 ⇔ x − 2x +1 = 31− x ⇔ x − x − 30 = 0 0,25
⇔ (x − 6)(x + 5) = 0 ⇔ x = 6 (TM) hoặc x = 5 − (loại) 0,25
Vậy PT đã cho có nghiệm: x = 6 0,25
x + y = 3 3 y = 3 3 − x Ta có:   ⇔  0,25 1 3
 x − 2y = 4 3 3  x − 2  (3 3−x)= 4 3
y = 3 3 − x
y = 3 3 − x ⇔  ⇔  0,25 2 5  x =10 3 x = 2 3 x = 2 3 x = 2 3 ⇔  ⇔  0,25 y = 3 3 − 2 3 y = 3
Vậy HPT đã cho có nghiệm: ( ; x y) = (2 3; 3) 0,25
 3+ x x x −3x + 9 x   6 P   :   3  = − −
, với x ≥ 0, x ≠ 9 .  x − 3 x x + 27   x + 3   x 0,25 x (x−3 x + + 9 3 )  3 x +9−6 P   = −  x − 
( x +3)(x−3 x +9) : 3  x + 3  1  3+ x x  x + 3 P =  − .  0,25 x 3 x 3  − + 3 x +   3 ( + x)2 3
− x ( x −3) x +3 9( x + )1 P = x + 3 ( = . 0,25
x − 3)( x +3) .3 x +3 ( x −3)( x +3) 3( x + )1 2 3 P = . Vậy 3 P =
, với x ≥ 0, x ≠ 9 0,25 x − 3 x − 3
Toạ độ giao điểm của hai đường thẳng y = 3x − m và y = 2x + 5 là nghiệm của y = 2x + 5 3
 x − m = 2x + 5 x = m + 5 HPT:  ⇔  ⇔ 0,25 y 3x m y 2x 5  = − = + y = 2m +15 Theo bài ra: 2 x − xy = 66 − , ta có: (m + )2
5 − (m + 5)(2m +15) = 66 − 2 0,25 2
⇔ m +15m −16 = 0 ⇔ (  = m − )(m + ) m 1 1 16 = 0 ⇔  0,25 m = 16 −
Vì m là số dương, nên m = 1 (TM); m = - 16 (loại)
Vậy m = 1 thoả mãn yêu cầu đề bài. 0,25
Gọi vận tốc dự định của ô tô khi đi từ A đến B là x (km/h); ĐK: x > 10
Thời gian ô tô dự định đi từ A đến B là: 260 (h) 0,25 3 1 x
Thời gian ô tô đi trên quãng đường 100 (km) đầu là: 100 (h) 0,25 x
Độ dài quãng đường còn lại là: 260 - 100 = 160 (km)
Vận tốc ô tô đi trên quãng đường 160 (km) còn lại là: x - 10 (km/h)
Thời gian ô tô đi trên quãng đường còn lại là: 160 (h) x −10 Đổi 48 (phút) = 4 (h) 5 0,25 Ta có PT: 100 160 260 4 + = + x x −10 x 5 100 160 260 4 2 + =
+ ⇒ x −10x − 2000 = 0 x x −10 x 5 ⇔ (  = x − )(x + ) x 50(TM ) 50 40 = 0 ⇔ 0,25  x = 40( − L)
Vậy vận tốc dự định của ô tô khi đi từ A đến B là: 50 (km/h) * PT: 2 x − (m − ) 2 2
2 x + m − 4m − 5 = 0 (1)
Ta có: ∆ = (m − )2 − ( 2 ' 2
1. m − 4m − 5) = 9 > 0 với mọi m. 0,25
=> PT luôn có hai nghiệm phân biệt x ; x với mọi m. 1 2
Tính được hai nghiệm: x = m − 5; x = m +1 1 2 0,25
* TH1: x = m − 5; x = m +1; mà + = 1 2 x 6 x 1 2
Ta có: m +1 = m +1 (ĐK: m ≥ 1 − ) 0,25 2 ⇔ (  =
m + )2 = m + ⇔ m(m + ) m 0 1 1 1 = 0 ⇔  (TM ) m = 1 −
* TH2: x = m − 5; x = m +1; mà + = 2 1 x 6 x 1 2
Ta có: m + 7 = m − 5 (ĐK: m ≥ 5 ) ⇔ (m + )2 2
7 = m − 5 ⇔ m +14m + 49 = m − 5 0,25 2 2  13  47
⇔ m +13m + 54 = 0 ⇔ m − + =  (vô lí) 2    4
Vậy m = 0; m = -1 thoả mãn yêu cầu đề bài. M ( áy bay) C Hình vẽ 400 300 B H A 4 1
Vì khoảng cách giữa hai người quan sát là 300 (m) nên AB = 300 (m) 0,25 Xét ∆ BHC vuông tại H 0
⇒ BH = CH.cot B = CH.cot 30 0,25 Xét ∆ CHA vuông tạ H 0
⇒ AH = CH.cot A = CH.cot 40 0,25
Ta có: AB = BH + AH ⇒ CH ( 0 0 . cot 30 + cot 40 ) = 300
⇒ CH ≈103(m) 0,25
Vậy máy bay cách mặt đất khoảng 103 (m) M E O F H Hình vẽ D P 0,25 N R I 2a T K
* Chứng minh tứ giác MPDF nội tiếp. 0,25
* Vì tứ giác MPDF nội tiếp  =  PDK PMN * Ta có:  = 
KPN PMN (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng 0,25 chắn cung PN). Do đó:  = 
PDK KPD nên tam giác KPD cân tại K. 0,25
* Chứng minh: ∆ KPT đồng dạng ∆ KMP (g.g) 2
⇒ KP = KT.KM 0,25
Mà ∆ KPD cân tại K => KP = KD 2
⇒ KD = KT.KM * Ta có: 2 = . KD KM KD KT KM ⇒ =
và ∆ KDT và ∆ KMD có  K chung KT KD
=> ∆ KDT đồng dạng với ∆ KMD 0,25 =>  =  ⇒  =  KDT KMD RDT TMI 2b Mà  = 
TMI TPI (cùng chắn cung IT) =>  =  RDT TPI (1)
* Tứ giác PMNT nội tiếp đường tròn (O) ⇒  +  0 PMN NTP =180 Mà  =  ⇒  +  0 PDK PMN PDR RTP =180
=> Tứ giác PDRT nội tiếp =>  =  TPR TDR (2) 0,25 Từ (1) và (2) ⇒  =  TPI TPR
=> Hai tia PI, PR trùng nhau.
=> Ba điểm P; I; R thẳng hàng. Ta có: 2 2
a + b + ab = (a + b)( a + b) 1 3 8 14 4 3 2 ≤ (4a + 6b) 2 2 2 a a 0,25 ⇒ ≥ 2 2
3a + 8b +14ab 2a + 3b 2 2 2 2 Tương tự: b b ≥ ; c c ≥ 0,25 2 2
3b + 8c +14bc 2b + 3c 2 2
3c + 8a +14ca 2c + 3a 2 2 2 5 Suy ra: a b c M = + + 2 2 2 2 2 2
3a + 8b +14ab
3b + 8c +14bc
3c + 8a +14ca 0,25 a b c
(a +b + c)2 2 2 2 a + b + c ≥ + + ≥ =
2a + 3b 2b + 3c 2c + 3a 5a + 5b + 5c 5 ab ac bc 15 M + + ⇒ ≥ = = 3 5 5 0,25
Dấu bằng xảy ra ⇔ a = b = c = 5
Vậy giá trị nhỏ nhất của M = 3 khi a = b = c = 5
Chú ý: HS làm theo cách khác đúng vẫn cho điểm tối đa.