

Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ VÀO THPT LẦN I HUYỆN VỤ BẢN NĂM HỌC 2024- 2025 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Không kể thời gian giao đề)
Phần I. Trắc nghiệm (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1. Điều kiện xác định của biểu thức 1 x − 2 + là 3 x − 4 x ≥ 2 A. x ≥ 4 . B. x > 4 . C. x ≥ 2 . D. . x ≠ 4
ax + 2y = b + 5
Câu 2. Biết hệ phương trình có nghiệm ( ; x y)=(2 )
;1 . Khi đó a +b bằng by
− ax = a + 2 A. 9. B. 18. C. 18 − . D. 9 − .
Câu 3. Hàm số nào sau đây nghịch biến trên R ? A. 2 y = 2x . B. y = ( − ) 2 1 3 x .
C. y =1− 3x .
D. y = 5x −1.
Câu 4. Cho phương trình 2
x + 4x −5=0 . Gọi x , x là hai nghiệm của phương trình. Giá trị của biểu 1 2 thức 2
A=(x − x ) là 1 2 A. −36 . B. 36. C. 16. D. 16 − .
Câu 5. Cho hàm số y = f (x) = ( 2 m − ) 2
4 x . Tất cả các giá trị của m để f (− ) 1 =5 là A. m=3 . B. m = − 3. C. m=4. D. m = ±3.
Câu 6. Cho tam giác ABC vuông tại A , đường cao AH . Cho AH = 4cm , BH = 2HC . Độ dài BH bằng A. 4 2 cm . B. 2 2 cm . C. 2 cm . D. 8cm .
Câu 7. Cho tam giác A
∆ BC vuông cân tại A , biết AB = 4cm . Bán kính đường tròn ngoại tiếp tam giác ABC bằng A. 4cm . B. 4 2 cm . C. 2cm . D. 2 2 cm .
Câu 8. Ngày 04 − 06 –1783, anh em nhà Mông–gôn–fi-ê (Montgolfier ) người Pháp phát minh ra
khinh khí cầu dùng không khí nóng. Coi khinh khí cầu này là hình cầu đường kính 11 m .
Diện tích mặt khinh khí cầu đó bằng A. 484π 2 π m . B. 121 2 m . C. 2 121π m . D. 2 121 m . 3 3
Phần II. Tự luận (8,0 điểm) Bài 1. (1,5 điểm)
a) Chứng minh đẳng thức: − ( − )2 2 3. 3 2 − 12 = 7 − 1− 3 b) Rút gọn biểu thức:
15 x −11 3 x − 2 2 x +3 A = + −
với x ≥ 0 và x ≠ 1.
x + 2 x − 3 1− x x + 3 2
Bài 2. (1,5 điểm) Cho phương trình 2 x − 2(2m+ ) 1 x − 3 = 0 ( ) 1 ( m là tham số). a) Giải phương trình ( ) 1 với m = 2 − .
b) Tìm tất cả các giá trị của m để phương trình ( )
1 có hai nghiệm phân biệt x , x thỏa mãn 1 2
x > x và 2 x = 1 + x 1 2 1 2 2
x − xy + 2= 0
Bài 3. (1,0 điểm) Giải hệ phương trình 2
y − xy − x −1=0 Bài 4. (3,0 điểm).
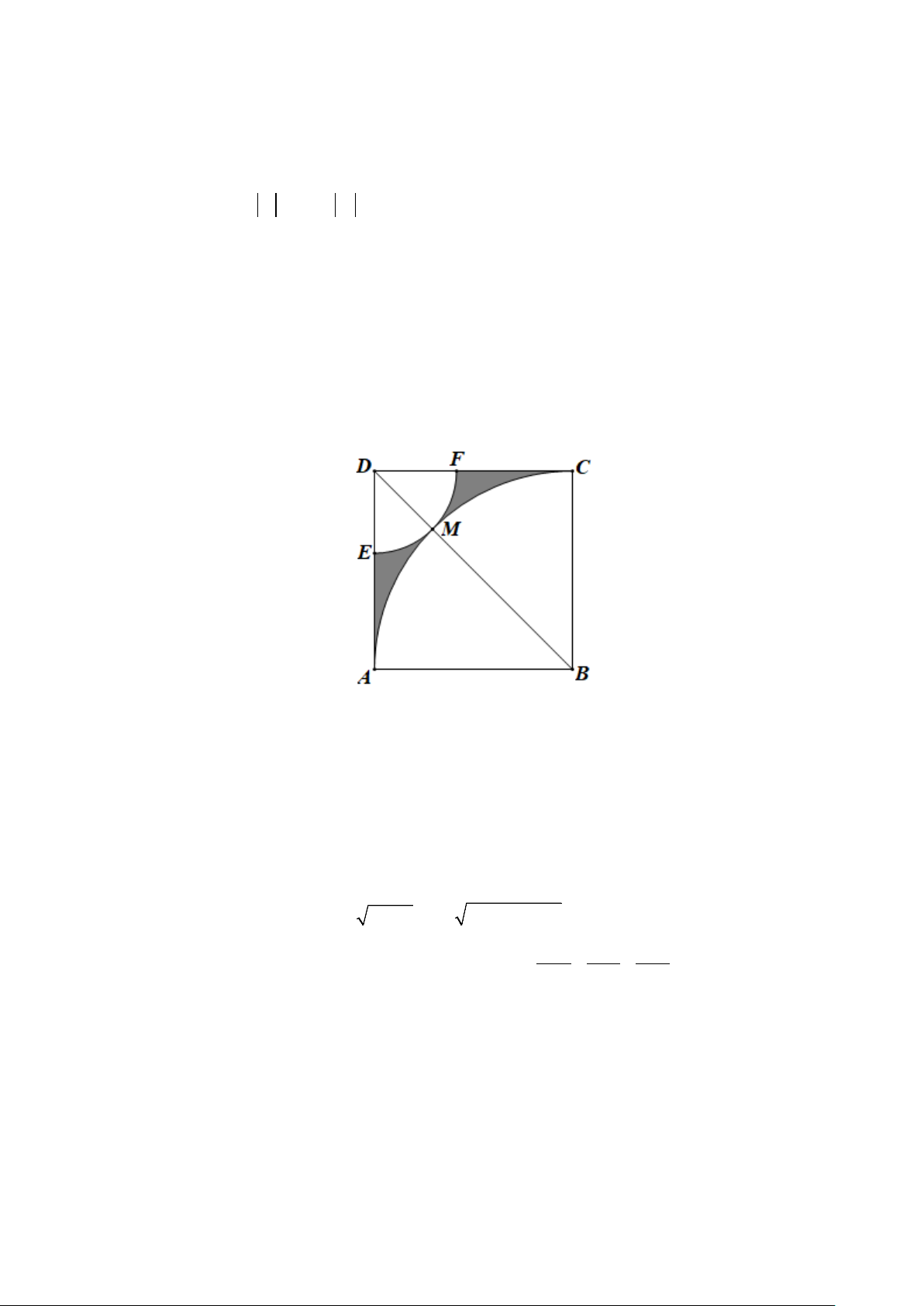
1. Cho hình vuông ABCD có chu vi là 40c . m Vẽ cung tròn ( ;
B BA) cắt đường chéo BD tại M , cung tròn ( ;
D DM ) cắt các cạnh ,
DA DC lần lượt tại E, F ( hình vẽ bên). Tính diện tích
phần hình vuông ABCD ở ngoài hai cung tròn. (phần tô đậm trong hình, kết quả làm tròn đến
chữ số thập phân thứ hai).
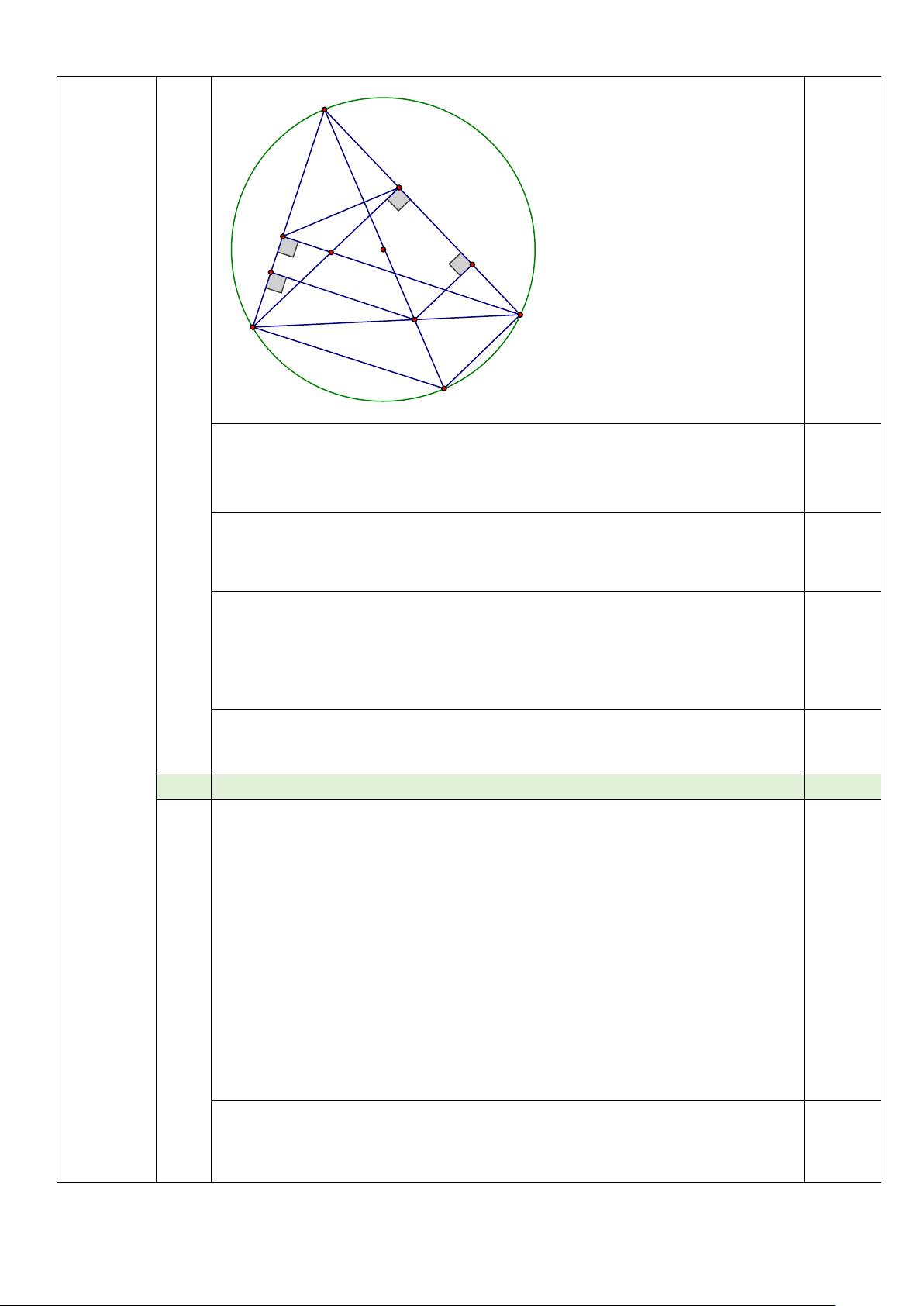
2. Cho tam giác nhọn ABC ( AB < AC) nội tiếp đường tròn tâm O,có 2 đường cao BE, CF
(E ∈AC,F ∈AB)cắt nhau tại H . Tia AO cắt BC tại M và cắt (O) tại N.
a) Chứng minh tứ giác B E
F C nội tiếp và = E A F ANC
b) Gọi P,Q lần lượt là hình chiếu của M trên AB, AC. Chứng minh H ∆ E F ∽ NCB ∆ và
HE.MQ.HB = HF .MP.NC Bài 5. (1,0 điểm) a) Giải phương trình: 2
x + 2x − 3 =1+ 5x −12x + 8
b) Cho a,b,c là các số thực dương thỏa mãn a b c + + = 2 . Chứng minh rằng :
a +1 b +1 c +1
ab + bc + ca ≥12
--------------------- HẾT--------------------- 3
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐÁP ÁN ĐỀ THI THỬ LẦN 1 TUYỂN SINH VÀO LỚP 10 THPT HUYỆN VỤ BẢN NĂM HỌC 2024-2025
I. Phần trắc nghiệm (2 điểm)
Mỗi câu lựa chọn đúng đáp án được 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án D C C B D A D C
II. Phần tự luận (8 điểm) BÀI Ý NỘI DUNG ĐIỂM
1.1 Chứng minh − ( − )2 2 3. 3 2 − 12 = 7 − 1− 3 0,5 − ( − )2 2 3 . 3 2 − 12 1− 3 2(1+ 3) = −3. 3 − 2 − 2 3 0,25 2 − = 1 − − 3 −3.(2− 3)−2 3 = 1 − − 3 −6+3 3 − 2 3 = 7 − 0,25 Vậy − ( − )2 2 3 3 2 − 12 = 7 − 1− 3 Bài 1 (1,5điểm) x − x − x +
1.2 Rút gọn biểu thức: 15 11 3 2 2 3 A = + −
với x ≥ 0 và x ≠ 1 1,0
x + 2 x − 3 1− x x + 3
15 x −11 3 x − 2 2 x +3 A = + −
với x ≥ 0 và x ≠ 1
x + 2 x − 3 1− x x + 3 15 x 0,25 −11 3 x − 2 2 x +3 A = ( − − x − ) 1 ( x +3) x −1 x + 3
(3 x −2)( x +3) (2 x +3)( x x − − )1 15 11 A = ( − −
x − )1( x +3) ( x − )1( x +3) ( x +3)( x − )1
15 x −11− 3x − 7 x + 6− 2x − x +3 A = 0,25 ( x − ) 1 ( x +3) 4 5
− x + 7 x − 2 A = ( x − ) 1 ( x +3) 0,25
( x − )1(2−5 x) A = ( x − ) 1 ( x +3) 2−5 x A = x + 3 0,25 −
Vậy với x ≥ 0 và x ≠ 1 thì 2 5 x A = x + 3
2.1 Giải phương trình ( ) 1 với m = 2 − . 0,5
Với m = − 2 , phương trình trở thành 2 x + 6x −3=0 0,25 ' ∆ =9 + 3 =12 >0
Phương trình có 2 nghiệm phân biệt: x = − 3+ 2 3 ; x = 3 − − 2 3 0,25
Vậy m = − 2 thì phương trình có hai nghiệm x = − 3+ 2 3 ; x = 3 − − 2 3
Tìm tất cả các giá trị của m để phương trình ( )
1 có hai nghiệm phân biệt x , x 2.2 1 2 1,0
thỏa mãn x > x và 2 x =1+ x 1 2 1 2 Ta có . a c =1.( 3 − ) = 3
− < 0 với mọi m
Vậy mọi m phương trình luôn có hai nghiệm trái dấu. 0,25
x + x = 2 2m +1 (2) 1 2 ( )
ÁP dụng hệ thức Viét ta có 0,25
x .x = − 3 (3) 1 2 Bài 2 x > 0 1 (1,5điểm)
Do mọi m phương trình luôn có hai nghiệm trái dấu, mà x > x ⇒ 1 2 x < 0 2
Nên 2 x =1+ x ⇔ 2 x =1− x
⇔ x =1− 2 x 1 2 1 2 2 1
Thay x =1− 2 x vào (3) ta được phương trình 2 2x − x −3=0 2 1 1 1
⇔ (x +1 . 2x −3 =0 1 ) ( 1 ) 0,25
x = −1 (ktm) 1 ⇔ 3 x = tm 1 ( ) 2 Với 3
x = ⇒ x = − 2 1 2 2 Thay 3
x = ; x = − 2 vào (2) tìm được 5 m − = 1 2 2 8 0,25 Vậy 5 m − = là giá trị cần tìm 8 2
x − xy + 2= 0 3
Giải hệ phương trình 1,0 2
y − xy − x −1=0 Bài 3 2 (1,0điểm)
x − xy + 2= 0 (1) 2
y − xy − x −1=0 (2) 0,25 Giải (2) : 2
y − xy − x −1=0 5 ⇔ ( y + )
1 ( y − x − ) 1 =0
⇔ y +1 =0 hoặc ⇔ y = x +1
Với y +1 =0 ⇔ y = −1.
Thay y = -1 vào phương trình ( )
1 ta được phương trình 2 x + x + 2 = 0 Phương trình này có 0,25 ∆ = 1– 4.2 = 7 − < 0
⇒ Phương trình vô nghiệm
Với y = x +1, thay y = x +1 vào (1) ta được 2
x − .x( x + ) 1 + 2=0 0,25 ⇔ x = 2 ⇒ y =3 Vậy hệ có nghiệm ( ; x y) = ( 2; 3 ) 0,25 4.1 1,0
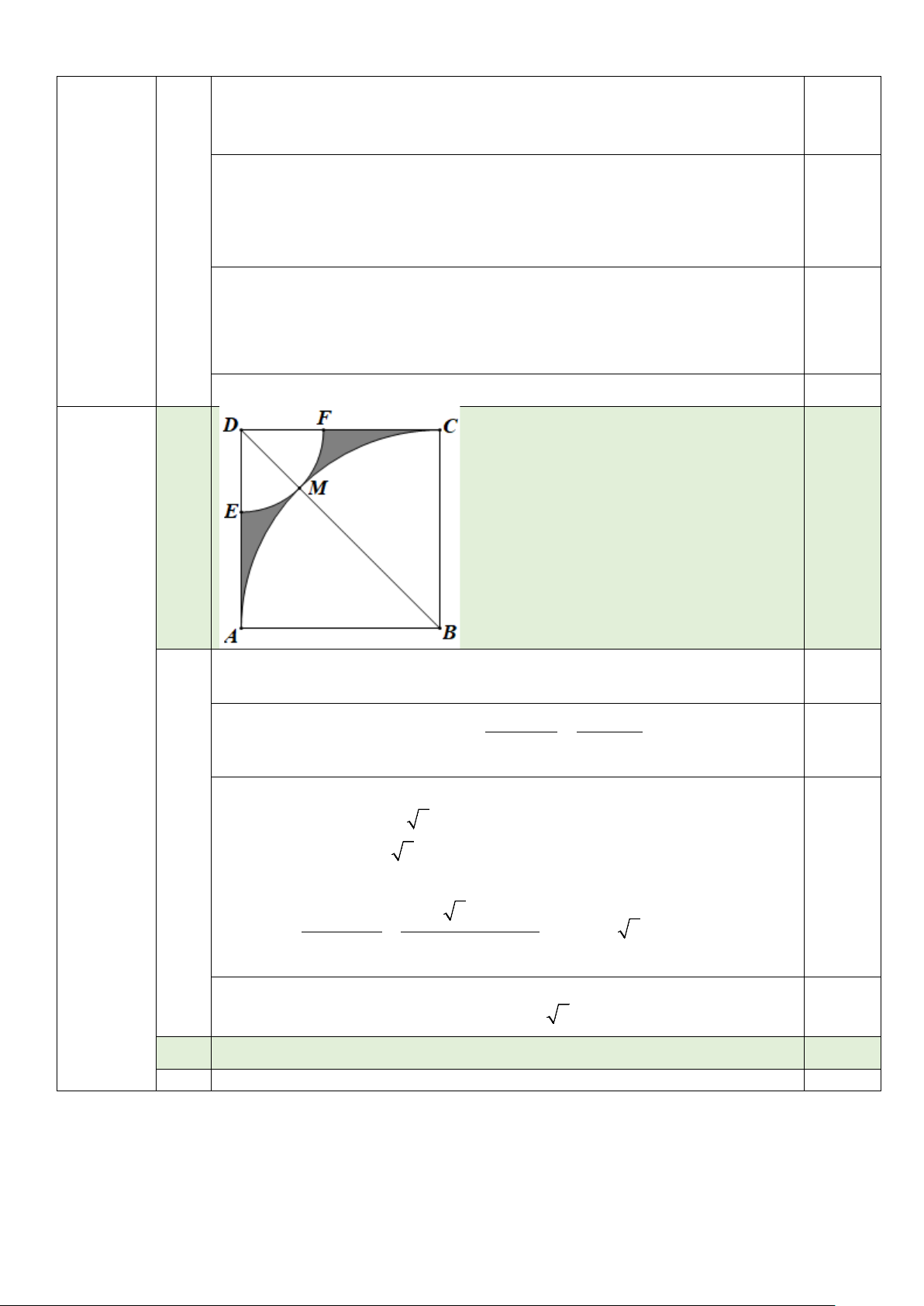
Độ dài cạnh hình vuông AB = 40 : 4 =10 cm
Diện tích hình vuông là 2 2 2
S = AB =10 =100(cm ) 0,25 1 2 2 π.AB .90 π.10 .90 2 Bài 4
Diện tích quạt tròn BAC là S = = = 25π cm 2 ( ) 360 360 0,25 (3,0điểm)
Xét tam giác ABD vuông tại A có 2 2 2 2
BD = AB + AD ⇒ BD =100+100
Từ đó tính được BD =10 2 (cm)
⇒ DM = BD− BM =10 2 −10 (cm)
Diện tích quạt DEF : 0,25 π π . DM (10 2 −10)2 2 .90 . .90 S = = = (75−50 2)π ( 2 cm 3 ) 360 360
Diện tích cần tính là:
S = S − S − S =100 − 25π − (75−50 2)π ≈ 7,98( 2 cm 0,25 1 2 3 )
4.2a Chứng minh tứ giác B E
F C nội tiếp và = AEF ANC . 1,0 6 A E F O H Q P C B M N
BE ⊥ AC ( gt) => 0 BEC =90 0,25
Chứng minh tương tự ta được 0 BFC =90 Xét tứ giác B E F C có = BEC BFC
Mà E, F là hai đỉnh kề 0,25 Vậy tứ giác B E
F C nội tiếp (dhnb) Vì tứ giác B E F C nội tiếp( cmt) ⇒ + 0 FBC E
F C =180 ( tc) Mà 0,25 + 0 E A F E
F C =180 ( hai góc kề bù) ⇒ = FBC AEF Mà
ABC = ANC ( Hai góc nội tiếp cùng chắn AC ) 0,25 ⇒ = AEF ANC
4.2b Chứng minh H ∆ E F ∽ NCB ∆ và HE.M .
Q HB = HF.M . P NC 1,0
Do AN là đường kính của (O) ⇒ 0
ABN = 90 ( góc nội tiếp chắn nửa đường tròn) ⇒ BN ⊥ AB
⇒ BN HC ( vì cùng vuông góc với AB )
Chứng minh tương tự ta được BH CN
⇒ tứ giác BHCN là hình bình hành 0,25
Do BN HC ⇒ = HCB
CBN ( hai góc so le trong)
Lại có tứ giác B E F C nội tiếp ⇒ = FCB E
F B ( hai góc nội tiếp cùng chắn BF ) ⇒ = = E F H CBN ( HCB)
Chứng minh tương tự ta được = EFH BCN Xét E HF ∆ và NCB ∆ 0,25 Có = E F H CBN 7 = EFH BCN ⇒ H ∆ E F ∽ NCB ∆ (g.g)
Xét tam giác ANC có MQ NC ( cùng vuông góc với AC ) MQ AM ⇒ = NC AN
Chứng minh tương tự ta được MP AM = 0,25 NB AN MQ MP MQ NC ⇒ = ⇒ = NC NB MP NB Mà ∆ E HF NC HF ∽ NCB ∆ ⇒ = HE NB MQ HF ⇒ = ⇒ MQ.HE = . MP HF 0,25 MP HE
Mà HB = NC ( Tứ giác BHCN là hình bình hành )
⇒ MQ.HE. HB = M . P HF.NC
5.1 Giải phương trình 2
x + 2x − 3 =1+ 5x −12x + 8 0,50 2
x + 2x − 3 =1+ 5x −12x + 8 ( ĐK: 3 x ≥ ) 2 ⇔ x − + x − = (x − )2 1 2 3 5 1 − (2x −3)
Đặt a = x −1;b = 2x −3 ( a > 0 vì 3
x ≥ ; b ≥0 ) 2 0,25 Phương trình trở thành 2 2
a +b = 5a −b ⇔ (a +b)2 2 2
= 5a −b ( vì a > 0,b ≥0 ⇒ a + b > 0)
⇔ (a −b)(2a +b) = 0 Bài 5
⇔ a = b ( vì a > 0,b ≥0 ⇒ 2a + b > 0 ) (1,0điểm)
Từ đó ta được 2x −3 = x −1
⇔ x − = (x − )2 2 3 1 ( vì 3
x ≥ ⇒ x −1 >0 ) 2 2 ⇔ x − 4x + 4=0 ( ) 0,25
⇔ x = 2 ( Thỏa mãn điều kiện)
Vậy phương trình có nghiệm x = 2
Cho a,b,c là các số thực dương thỏa mãn a b c + + = 2 . 5.2
a +1 b +1 c +1 0,50
Chứng minh rằng : ab + bc + ca ≥12
Từ giả thiết ta có: a b c 1 1 =1 − +1− = + a +1 b +1
c +1 b +1 c +1 0,25
Áp dụng bất đẳng thức Cauchy ta có 8 1 1 2 + ≥ a 2 ⇒ ≥ b +1 c +1 (b+ )1(c+ )1 a +1 (b+ )1(c+ )1
Tương tự ta được b 2 ≥ ; c 2 ≥ b +1
(a+ )1(c+ )1 c +1 (b+ )1(a+ )1 Khi đó ta được a.b 4 ( ≥ a + ) 1 .(b + ) 1 (c+ ) 1 (b + ) 1 (a + ) 1 4 (b+ ) 1 (a + ) 1 ⇒ a. b ≥ ( c + ) 1 4 (b+ ) 1 (c + ) 1 4 (a + ) 1 (c + ) 1
Tương tự ta được : b. c ≥ ( ; a. c ≥ a + ) 1 (b+ )1 4 (b+ ) 1 (a + ) 1 4 (b+ ) 1 (c + ) 1 4 (c + ) 1 (a + ) 1 ⇒ a.b + . b c + . c a ≥ ( + + c + ) 1 (a+ )1 (b+ )1
Mặt khác theo bất đẳng thức Cauchy ta có (b+ )1(a+ )1 (b+ )1(c+ )1 (c+ )1(a+ )1 ( + + ≥ c + ) (a+ ) (b+ ) 3 1 1 1 ⇒ a.b + . b c + .
c a ≥ 12 dấu bằng xảy ra khi và chỉ khi a = b = c = 2 0,25
Vậy với a,b,c là các số thực dương thỏa mãn a b c + + = 2
a +1 b +1 c +1
thì ab + bc + ca ≥12




