SỞ GD-ĐT BẮC NINH
KIỂM TRA KHẢO SÁT CHẤT LƯỢNG LẦN 1
TRƯỜNG THPT HÀM LONG NĂM HỌC 2022-2023 MÔN: VẬT LÍ 12 --------------------
Thời gian làm bài: 50 PHÚT
(Đề thi có 5 trang)
(không kể thời gian phát đề) Số báo
Họ và tên: ............................................................................ Mã đề 101 danh: .............
Câu 1. Một dòng điện có cường độ I chạy trong vòng dây dẫn hình tròn bán kính R đặt trong chân không.
Cảm ứng từ tại tâm của vòng dây do dòng điện này gây ra có độ lớn là A. - I - R - R - I 7 B = 2 . p 10 . B. 7 B = 2 . p 10 . C. 7 B = 2.10 . D. 7 B = 2.10 . R I I R
Câu 2. Đối với dao động tuần hoàn, khoảng thời gian ngắn nhất mà sau đó trạng thái dao động của vật
được lặp lại như cũ được gọi là
A. chu kì riêng của dao động.
B. tần số riêng của dao động.
C. tần số dao động.
D. chu kì dao động.
Câu 3. Một sóng cơ truyền với tần số 10 Hz, sau khoảng thời gian 2 phút thì quãng đường sóng truyền
bằng bao nhiêu lần bước sóng? A. 7200. B. 3600. C. 2400. D. 1200.
Câu 4. Giao thoa sóng ở mặt nước với hai nguồn kết hợp đặt tại A và B dao động điều hòa cùng pha theo
phương thẳng đứng. Sóng truyền trên mặt nước có bước sóng λ. Cực tiểu giao thoa nằm tại những điểm
có hiệu đường đi của hai sóng từ hai nguồn tới đó bằng.
A. 2kλ với k = 0, ±1, ±2,…
B. (𝑘 + 0,5)𝜆 với k = 0, ±1, ±2,…
C. kλ với k = 0, ±1, ±2,…
D. (2𝑘 + 1)𝜆 với k = 0, ±1, ±2,…
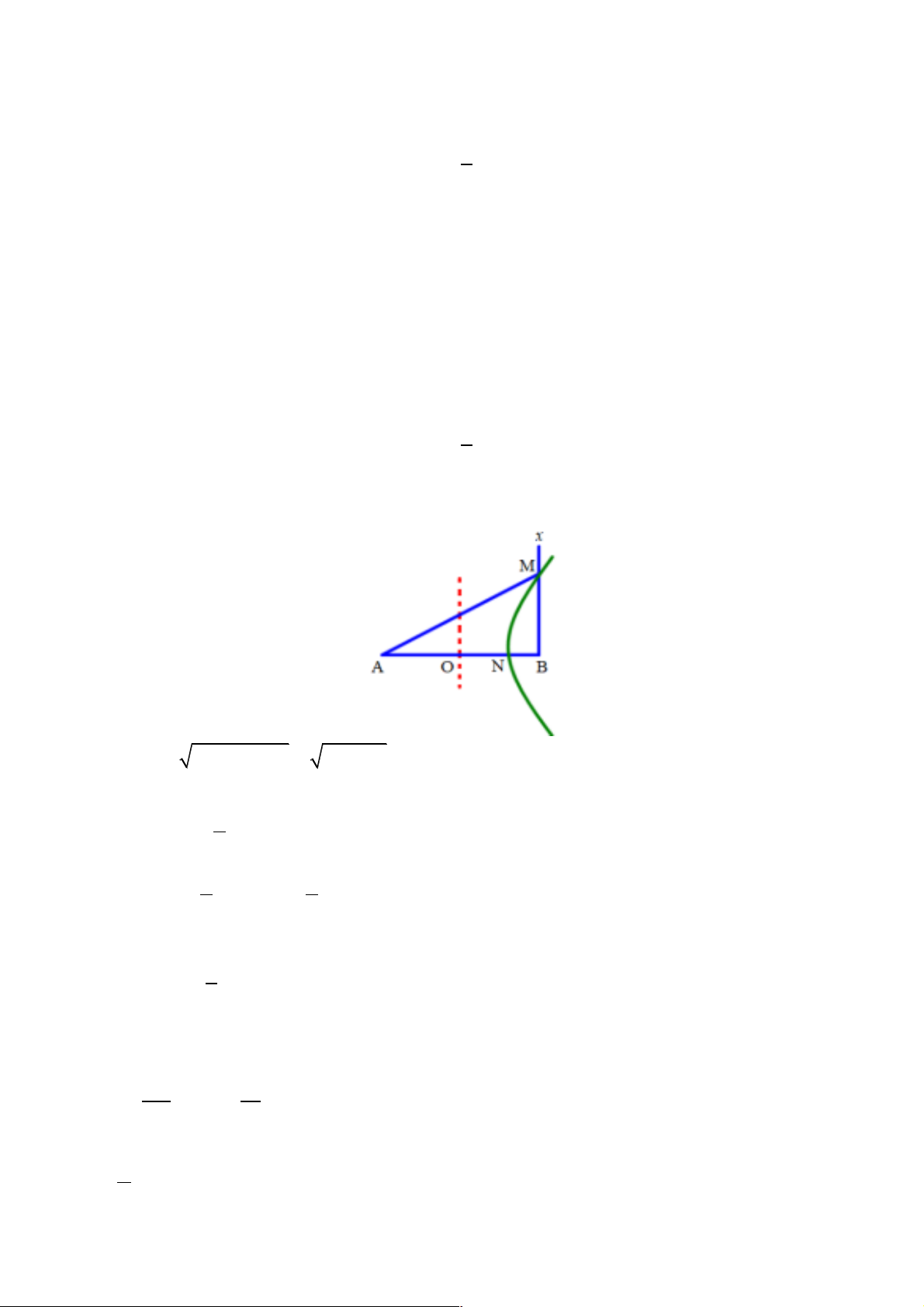
Câu 5. Tiến hành thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm A và B dao
động điều hòa cùng pha theo phương thẳng đứng. Biết AB = 12cm. Xét các điểm ở mặt nước nằm trên tia
Bx vuông góc với AB, M là điểm cực tiểu giao thoa gần B nhất và cách B một đoạn 5 cm. Trên tia Bx
khoảng cách từ điểm cực tiểu giao thoa gần B nhất đến điểm cực đại giao thoa xa B nhất là ℓ. Độ dài đoạn
ℓ gần nhất với giá trị nào sau đây? A. 11,5 cm. B. 7,5 cm. C. 5,5 cm. D. 4,5 cm.
Câu 6. Một con lắc lò xo gồm vật nặng và lò xo có độ cứng
k dao động điều hòa. Chọn gốc tọa độ O tại vị trí cân bằng, trục Ox song song với trục lò xo. Thế năng
của con lắc lò xo khi vật có li độ x là kx 2 kx 2 k x A. 2 W = kx B. W = C. W = . D. W = t t 2 t 2 t 2
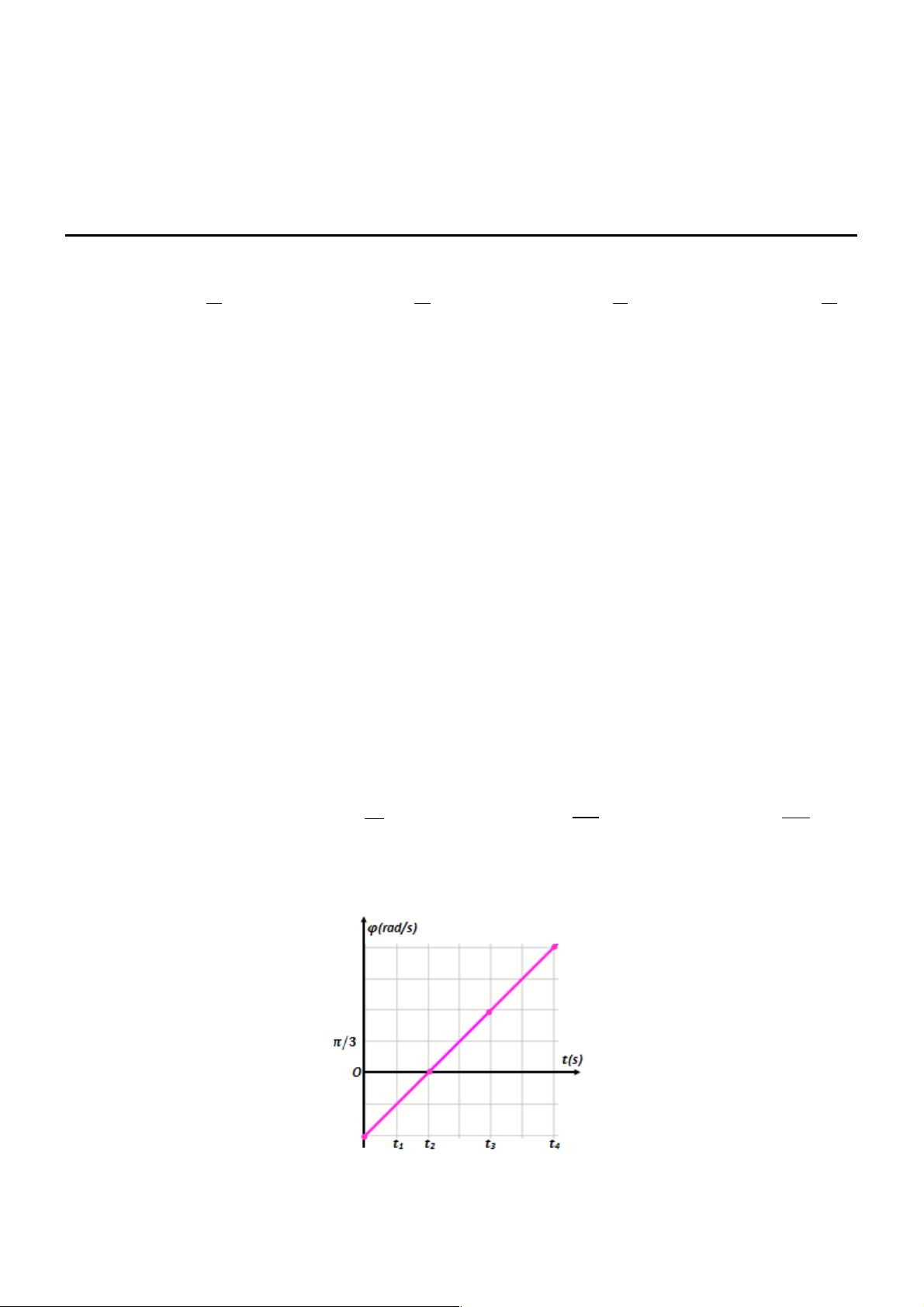
Câu 7. Một chất điểm dao động điều hòa có pha dao động của li độ quan hệ với thời gian được biễu diễn
như hình vẽ. Quãng đường chất điểm đi được từ thời điểm t3 đến thời điểm t4 là 10cm và t2 - t1= 0,5s. Độ
lớn gia tốc của chất điểm tại thời điểm t = 2018s gần giá trị nào nhất sau đây? A. 17cm/s2. B. 22cm/s2. C. 20m/s2. D. 14cm/s2.
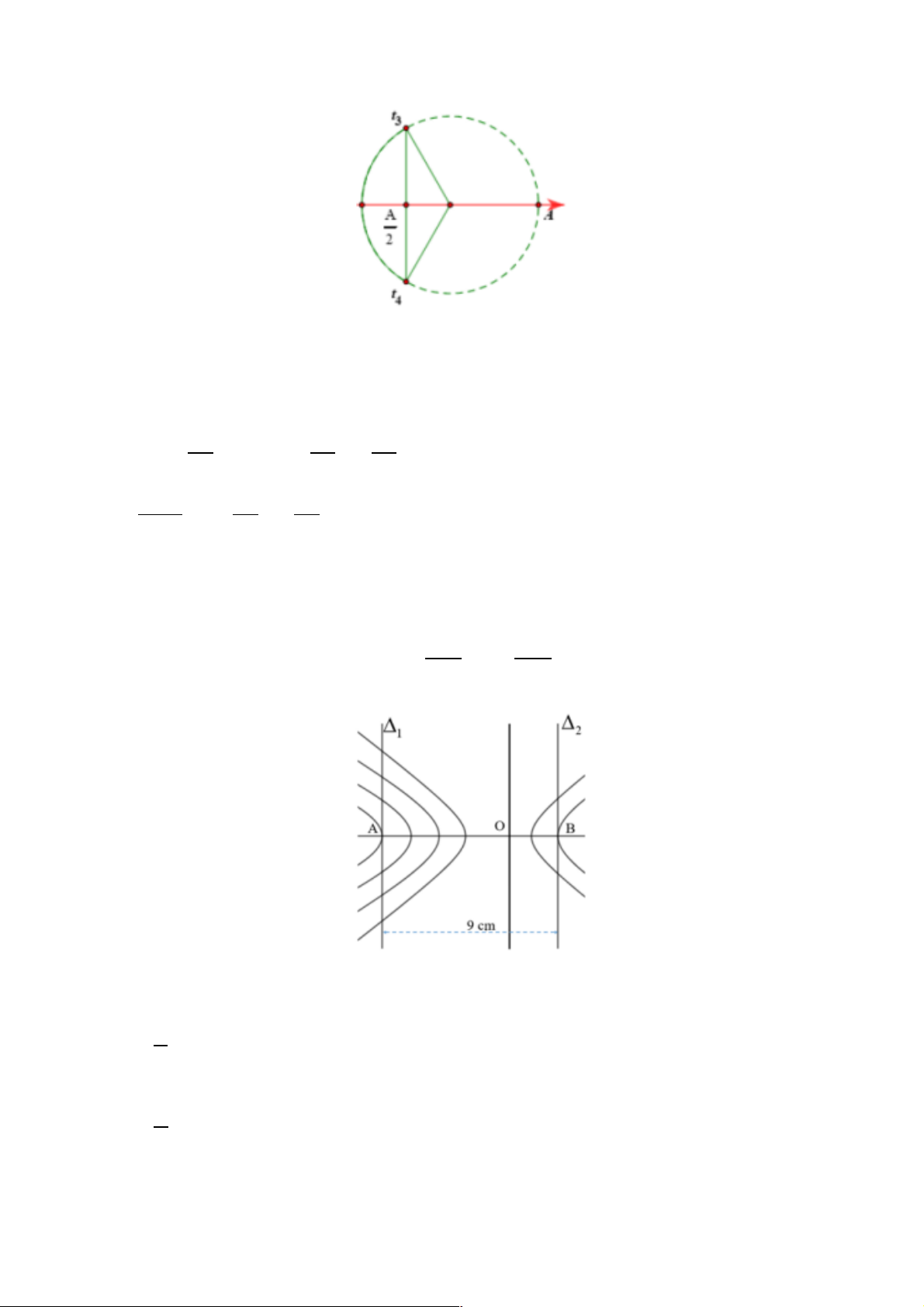
Câu 8. Ở mặt chất lỏng, tại hai điểm S và S cách nhau 28 cm có hai nguồn dao động cùng pha theo 1 2
phương thẳng đứng phát ra hai sóng kết hợp. Gọi D và D là hai đường thẳng ở mặt chất lỏng cùng 1 2 Trang 1
vuông góc với đoạn thẳng S S và cách nhau 9 cm. Biết số điểm cực đại giao thoa trên D và D tương 1 2 1 2
ứng là 7 và 3. Số điểm cực đại giao thoa trên đoạn thẳng S S là 1 2 A. 9. B. 17. C. 19. D. 7.
Câu 9. Một vật tham gia đồng thời hai dao động điều hòa cùng phương với li độ dao động lần lượt là x =
A1cos (ωt + φ1) và x2 = A2cos (ωt + φ2). Gọi φ là pha ban đầu của dao động tổng hợp, φ được tính theo
biểu thức nào dưới đây? A sin j - A sin j A sin j + A sin j A. 1 1 2 2 tan j = B. 1 1 2 2 tan j = A cos j - A cos j A cos j + A cos j 1 1 2 2 1 1 2 2 A cos j - A cos j A cos j + A cos j C. 1 1 2 2 tan j = D. 1 1 2 2 tan j = A sin j - A sin j A sin j + A sin j 1 2 2 2 1 2 2 2
Câu 10. Một vật có m = 500g dao động điều hoà với phương trình dao động x = 2cos10 p t(cm). Lấy 2 p
» 10. Năng lượng dao động của vật là A. 0,02J. B. 0,1mJ. C. 0,01J. D. 0,1J.
Câu 11. Một con lắc lò xo gồm vật nhỏ khối lượng m và lò xo nhẹ có độ cứng k đang dao động điều
hòa. Khi vật qua vị trí có li độ x thì lực kéo về là m
A. F = -mx B. 2 F = w - x C. F = - x D. 2
F = -mw x 2 w
Câu 12. Hiện tượng cộng hưởng cơ học xảy ra khi tần số của lực cưỡng bức
A. lớn hơn tần số dao động riêng của hệ.
B. nhỏ hơn tần số dao động riêng của hệ.
C. bằng tần số của dao động cưỡng bức.
D. bằng tần số dao động riêng của hệ.
Câu 13. Một dao động cưỡng bức với tần số riêng của hệ f0, lực cưỡng bức có biên độ F0, tần số f. Phát
biểu nào sau đây không đúng?
A. Tần số dao động là f0
B. Biên độ dao động không đổi.
C. Khi f càng gần f0 thì biên độ dao động càng lớn.
D. Biên độ dao động phụ thuộc F0.
Câu 14. Dòng điện có cường độ 2 A chạy qua một vật dẫn có điện trở 200Ω. Nhiệt lượng tỏa ra trên vật dẫn đó trong 40 s là A. 30 kJ. B. 20 kJ. C. 32 kJ. D. 16 kJ.
Câu 15. Mối liên hệ giữa tần số góc w và tần số f của một dao động điều hòa là 1 A. w = .
B. w = f .
C. w = 2pf . D. w = pf . 2pf 2p
Câu 16. Đối với con lắc đơn, đồ thị biểu diễn mối liên hệ giữa chiều dài ℓ của con lắc và chu kì dao động T của nó là
A. đường thẳng.
B. đường parabol.
C. đường elip. D. đường hyperbol.
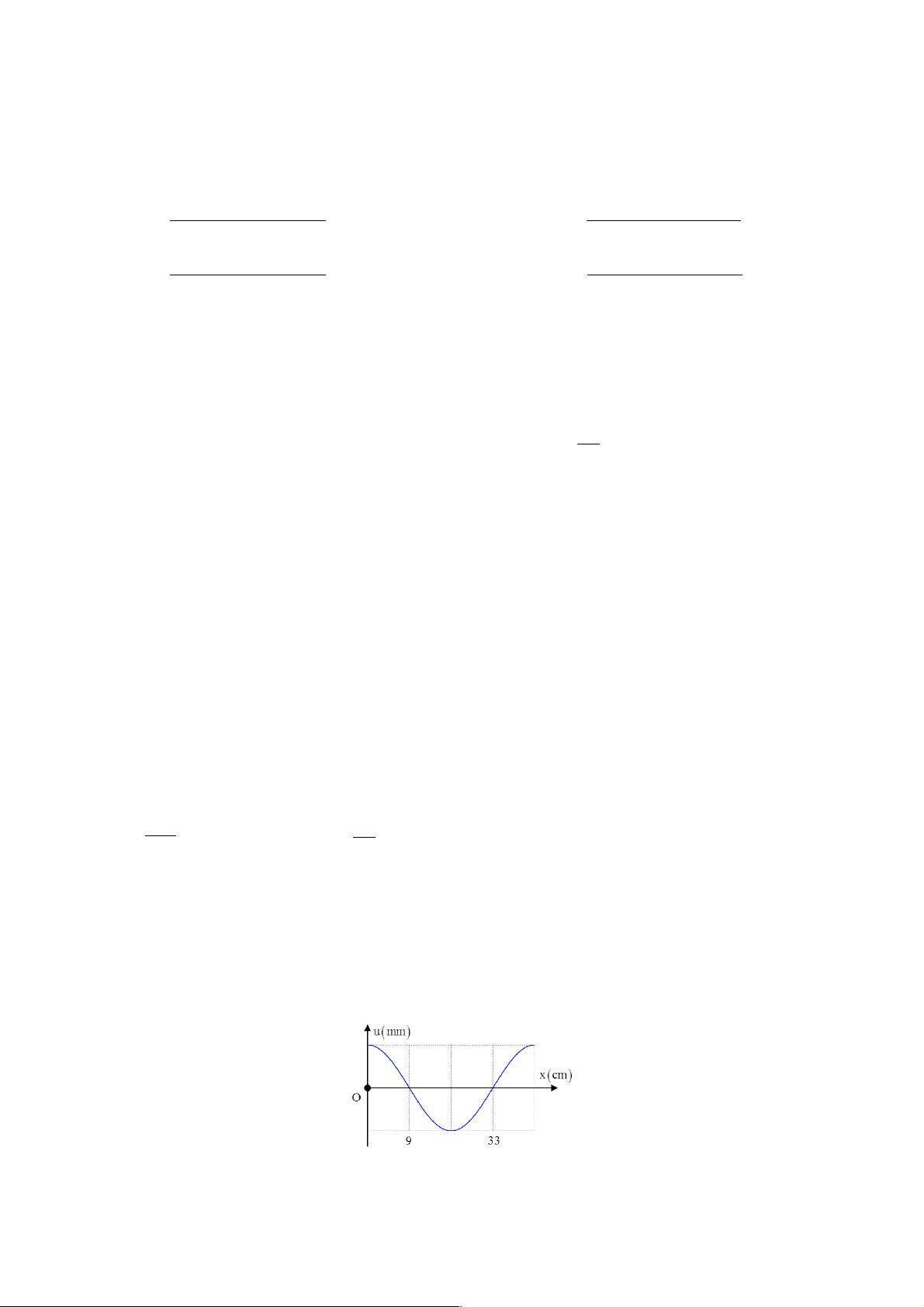
Câu 17. Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như
hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng A. 24 cm. B. 36 cm. C. 18 cm. D. 48 cm. Trang 2 æ p ö
Câu 18. Hai dao động điều hòa cùng phương, có phương trình x = Acos wt + và 1 ç ÷ è 3 ø æ 2p ö
x = Acos wt - là hai dao động 2 ç ÷ è 3 ø p p
A. ngược pha B. lệch pha . C. cùng pha. D. lệch pha . 2 3
Câu 19. Một con lắc đơn có chiều dài 0,5 m dao động điều hòa tại nơi có g = 9,8 2 m/s . Con lắc dao động với tần số góc là A. 9,8 rad/s. B. 28 rad/s. C. 4,4 rad/s. D. 0,7 rad/s.
Câu 20. Bước sóng là
A. quãng đường sóng truyền đi được trong thời gian một chu kỳ
B. quãng đường sóng truyền đi được trong một đơn vị thời gian.
C. khoảng cách giữa hai điểm của sóng có li độ bằng nhau
D. khoảng cách giữa hai gợn sóng gần nhau.
Câu 21. Con lắc lò xo gồm vật nhỏ nặng 1 kg thực hiện đồng thời hai dao động điều hoà theo phương
thẳng đứng, theo các phương trình: x = 5 2 cos10t cm và x = 5 2sin10t cm (Gốc tọa độ trùng với vị trí 1 2
cân bằng, t đo bằng giây và lấy gia tốc trọng trường g = 10 m/s2). Lực cực đại mà lò xo tác dụng lên vật là A. 10N. B. 20 N. C. 25 N. D. 0,25 N.
Câu 22. Hai dao động điều hòa cùng phương, cùng tần số có pha ban đầu là j và j . Hai dao động 1 2
ngược pha khi hiệu j -j có giá trị bằng 2 1 æ 1 ö A. (2n + ) 1 p với n = 0, 1 ± , 2, ± ... B. 2n + p với n = 0, 1 ± , 2, ± ... ç ÷ è 4 ø æ 1 ö C. 2n + p với n = 0, 1 ± , 2, ± ...
D. 2np với n = 0, 1 ± , 2, ± ... ç ÷ è 2 ø
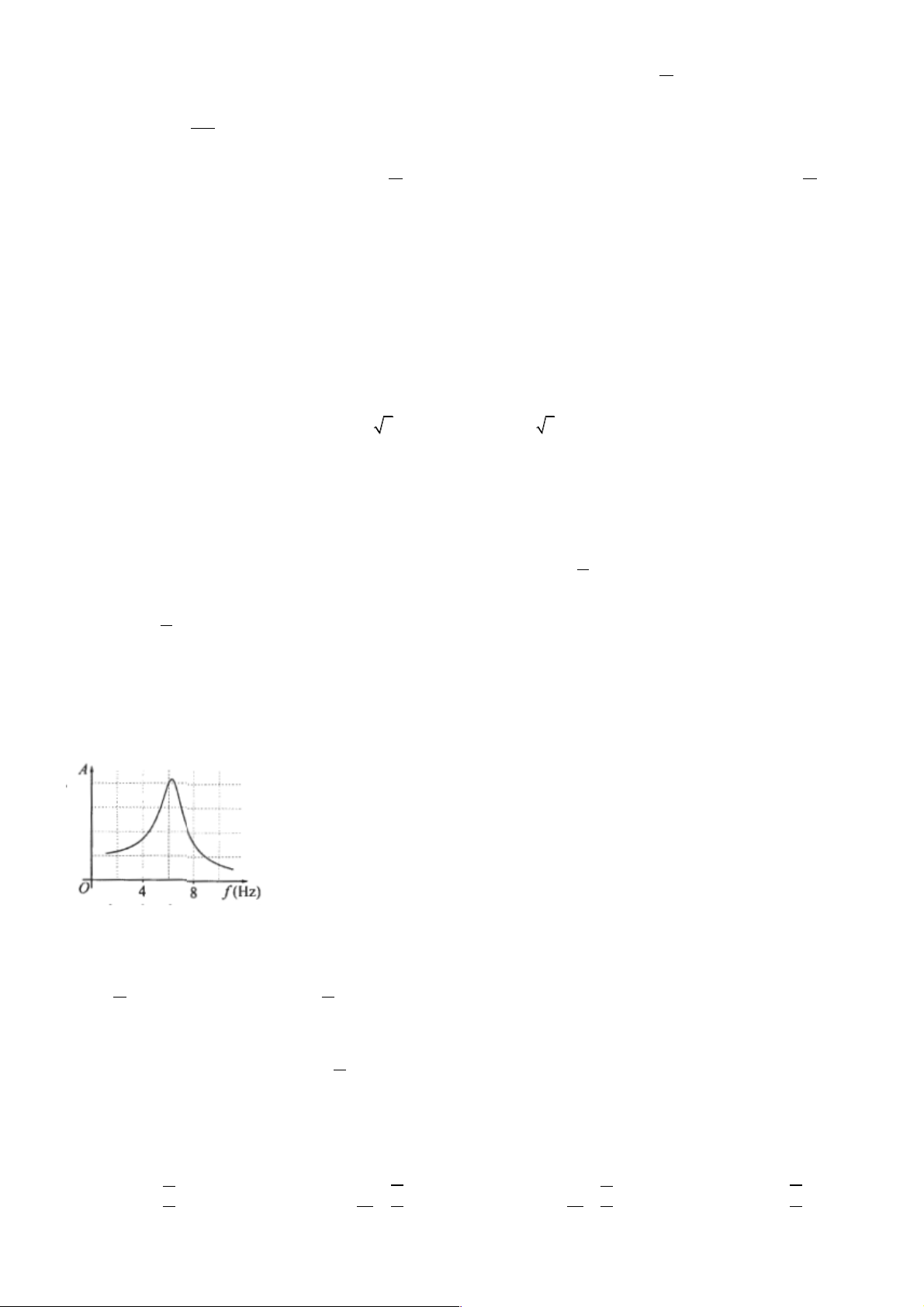
Câu 23. Tác dụng vào hệ dao động một ngoại lực cưỡng bức tuần hoàn có biên độ không đổi nhưng tần
số f thay đổi được, ứng với mỗi giá trị của f thì hệ sẽ dao động cưỡng bức với biên độ A. Hình bên là
đồ thị biểu diễn sự phụ thuộc của A vào f . Chu kì dao động riêng của hệ gần nhất với giá trị nào sau đây? A. 0,25 s. B. 0,45 s. C. 0,35 s. D. 0,15s.
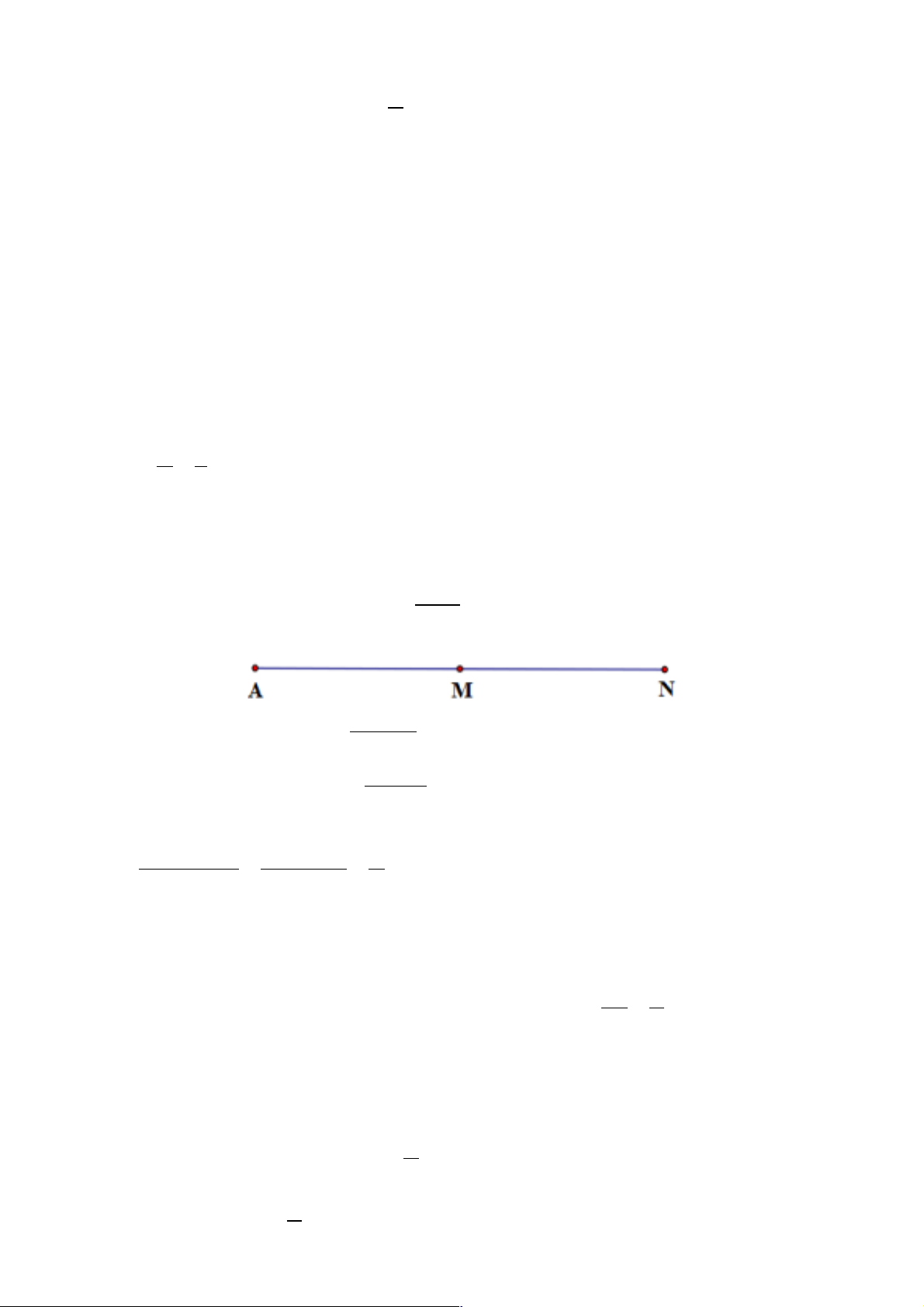
Câu 24. Cho ba điểm A, M, N theo thứ tự trên một đường thẳng với AM = MN. Đặt điện tích q tại điểm
A thì cường độ điện trường tại M có độ lớn là E. Cường độ điện trường tại N có độ lớn là E E A. B. C. 4E D. 2E 2 4
Câu 25. Một vật dao động điều hòa với phương trình x = A cos (2t + φ) cm. Tại thời điểm t1 vật có vận p
tốc là v = 5 cm/s; tại thời điểm t + s thì vận tốc của vật là 12 cm/s. Tốc độ trung bình mà vật đi được 2 4
trong một chu kì có giá trị gần nhất: A. 7,0 cm/s B. 9,0 cm/s C. 8,0 cm/s D. 9,5 cm/s
Câu 26. Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo nhẹ có độ cứng k, dao động điều hòa
với tần số góc là A. 𝜔 = .!.
B. 𝜔 = # . " . C. 𝜔 = # .!. D. 𝜔 = ." . " $% ! $% " !
Câu 27. Ứng dụng quan trọng nhất của con lắc đơn là Trang 3
A. xác định chiều dài con lắc
B. khảo sát dao động điều hòa của một vật
C. xác định chu kì dao động
D. xác định gia tốc trọng trường
Câu 28. Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là
A. biên độ và tốc độ.
B. li độ và tốc độ.
C. biên độ và gia tốc.
D. biên độ và năng lượng.
Câu 29. Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ có độ cứng 100 N / m dao động điều hoà. Khi qua vị
trí cân bằng thì động năng cực đại của vật là 0,5J. Biên độ dao động của vật là A. 10 cm. B. 5cm. C. 0,1cm. D. 1cm.
Câu 30. Nối một điện trở vào hai cực của một nguồn điện có suất điện động E thì dòng điện chạy trong
mạch có cường độ I. Trong thời gian t, công mà nguồn điện sinh ra bằng A. xIt B. 2 It x C. 0,5 I x t D. 2 xI t
Câu 31. Một nguồn dao động đặt tại điểm A trên mặt chất lỏng nằm ngang phát ra dao động điều hòa
theo phương thẳng đứng với phương trình u0 = Acos ωt. Sóng do nguồn dao động này tạo ra truyền trên
mặt chất lỏng có bước sóng λ tới điểm M cách A một khoảng x. Coi biên độ sóng và vận tốc sóng
không đổi khi truyền đi thì phương trình dao động tại điểm M là: A. uM = Acos wt B. uM = Acos(wt -px/l)
C. uM = Aacos(wt + px/l)
D. uM = Acos(wt -2px/l)
Câu 32. Một vật có khối lượng m dao động điều hòa với tần số góc w và biên độ dao động A. Mốc thế
năng tại vị trí cân bằng. Khi vật có li độ x = A thì thế năng của vật bằng 1 1 1 A. 0 B. 2 m A w C. 2 2 mw A D. 2 mw A 2 2 2
Câu 33. Con lắc đơn dao động điều hoà tại nơi có gia tốc trọng trường 9,81 m/s2, với chu kỳ T = 2s.
Chiều dài của con lắc là A. l = 0,040 m B. l = 96,60 cm C. l = 3,120 m D. l = 0,993 m æ p
Câu 34. Một chất điểm dao động điều hòa với phương trình ö x = 5cos 10t + (cm), trong đó x(cm), ç ÷ è 6 ø
t(s). Tại thời điểm vật có li độ 2,5cm thì tốc độ của vật là:
A. 2,5 3cm / s B. 25cm / s C. 25 3cm / s D. 25 2cm / s
Câu 35. Hệ thống giảm xóc ở ô tô là ứng dụng của
A. hiện tượng cộng hưởng cơ.
B. dao động tắt dần.
C. dao động duy trì.
D. dao động cưỡng bức.
Câu 36. Cho hai chât điểm dao động điều hòa cùng phương, chu kì 2 s với biên độ lần lượt là 3 cm và 4 2
cm. Biết khoảng thời gian trong một chu kì để x1x2 < 0 là t = (với x1 và x2 lần lượt là li độ của vật 1 và 3
vật 2). Biên động dao động tổng hợp của hai vật là A. 5 cm. B. 6,1 cm. C. 6,8 cm. D. 7 cm.
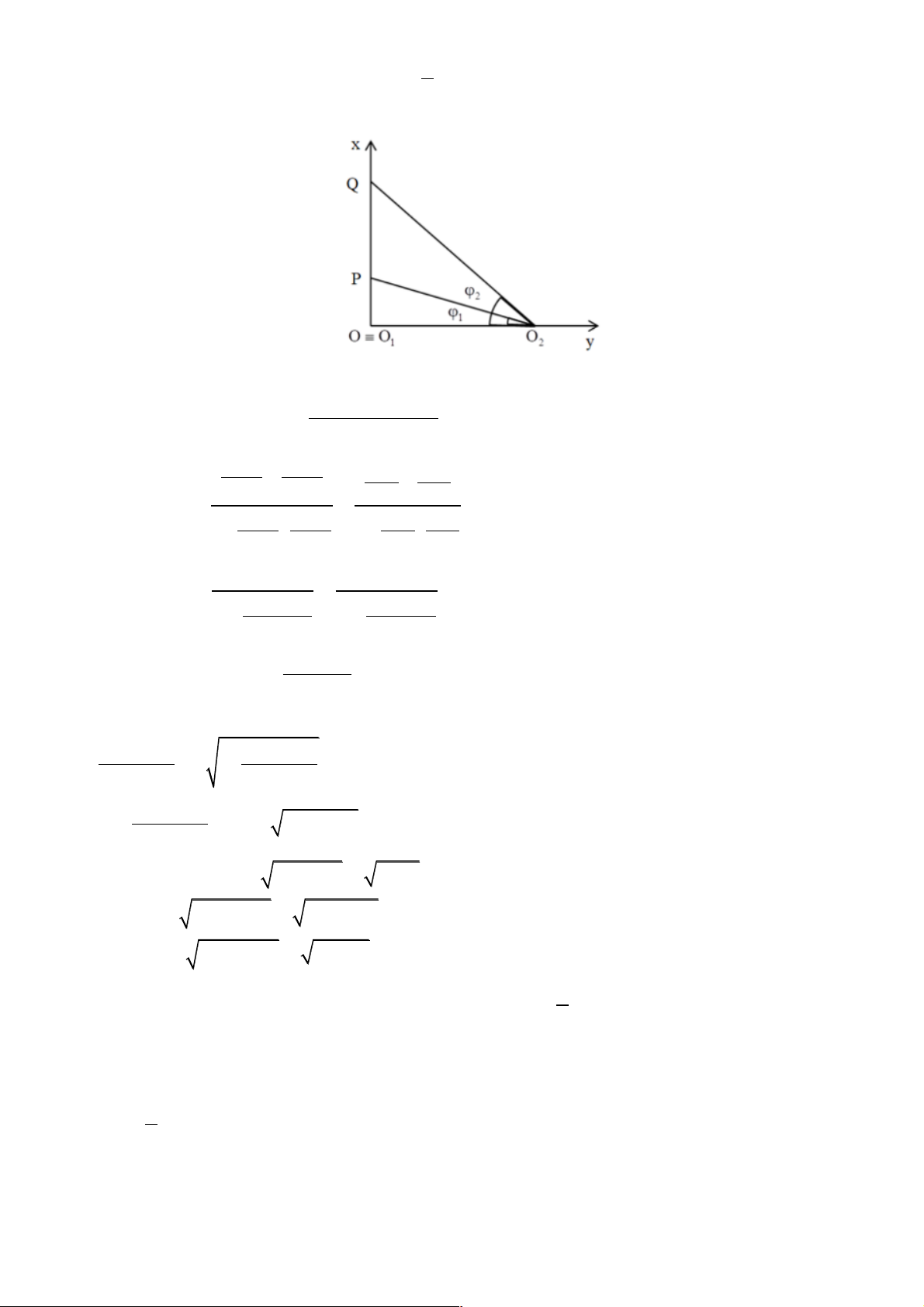
Câu 37. Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp 𝑂# và 𝑂$ dao động cùng
pha, cùng biên độ. Chọn hệ tọa độ vuông góc xOy (thuộc mặt nước) với gốc tọa độ là vị trí đặt nguồn 𝑂#
còn nguồn 𝑂$ nằm trên trục Oy. Hai điểm P và Q nằm trên Ox có OP = 4,5 cm và OQ = 8 m. Dịch
chuyển nguồn 𝑂$ trên trục Oy đến vị trí sao cho góc 𝑃𝑂$𝑄
2 có giá trị lớn nhất thì phần tử nước tại P
không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại
nào khác. Trên đoạn OP, điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn là A. 2,5 cm. B. 1,1 cm. C. 2,0 cm. D. 3,4 cm.
Câu 38. Trong giao thoa của hai sóng trên mặt nước từ hai nguồn kết hợp cùng pha nhau, những điểm
dao động với biên độ cực đại có hiệu khoảng cách tới hai nguồn (với k = 0; 1; 2; 3;...) là kl æ 1 ö k + l ç ÷ A. 2 B. 2kl C. è 2 ø D. kl
Câu 39. Con lắc đơn gồm sợi dây có chiều dài l và vật có khối lượng m, dao động điều hòa ở nơi có gia
tốc trọng trường g, khi sợi dây hợp với phương thẳng đứng góc α thì lực kéo về của biểu thức là Trang 4 mg a
A. P = -mgl . B. P = - .
C. P = -mga . D. P = - . t t a t t mg
Câu 40. Một vật dao động điều hòa theo phương trình x = Acos(ωt+φ) (với A > 0; w > 0). Đại lượng w được gọi là
A. li độ của dao động.
B. pha của dao động.
C. tần số dao động.
D. tần số góc của dao động.
------ HẾT ------ ĐÁP ÁN 1.A 2.D 3.D 4.B 5.C 6.C 7.B 8.C 9.B 10.D
11.D 12.D 13.A 14.C 15.C 16.B
17.D 18.A 19.C 20.A 21.B
22.A 23.D 24.B
25.C 26.D 27.D 28.D 29.A 30.A
31.D 32.C 33.D 34.C 35.B 36.B
37.C 38.D 39.C 40.D Câu 1 (NB): Phương pháp: - I
Cảm ứng từ tại tâm của dòng điện chạy trong dây dẫn uốn thành vòng tròn: 7 B = 2p.10 . R Cách giải: - I
Cảm ứng từ tại tâm của vòng dây do dòng điện này gây ra có độ lớn là: 7 B = 2p.10 . R Chọn A. Câu 2 (TH): Phương pháp:
Sử dụng lí thuyết về dao động. Cách giải:
Đối với dao động tuần hoàn, khoảng thời gian ngắn nhất mà sau đó trạng thái dao động của vật
được lặp lại như cũ được gọi là chu kì dao động. Chọn D. Câu 3 (VD): Phương pháp:
Bước sóng: λ = vT.
Quãng đường sóng truyền: S = v. t Cách giải:
Quãng đường sóng truyền sau 2 phút là:
S = vt = v. 2 . 60 = 120v 1 1 Bước sóng: l = . v T = . v = . v = 0,1v f 10 S 120v => = = 1200 => S = 1200l l 0,1v Chọn D. Trang 5
Câu 4 (NB): Phương pháp
Giao thoa sóng hai nguồn cùng pha:
+ Điều kiện có cực đại giao thoa: d - d = kl 2 1 æ 1 ö
+ Điều kiện có cực tiểu giao thoa: d - d = k + l 2 1 ç ÷ è 2 ø Cách giải:
Cực tiểu giao thoa nằm tại những điểm có hiệu đường đi của hai sóng từ hai nguồn tới đó bằng (k
+ 0,5) λ với k = 0, ±1, ±2, … Chọn B. Câu 5 (VDC): Phương pháp:
* Giao thoa sóng hai nguồn cùng pha:
+ Điều kiện có cực đại giao thoa: d - d = kl 2 1 æ 1 ö
+ Điều kiện có cực tiểu giao thoa: d - d = k + l 2 1 ç ÷ è 2 ø
* Vẽ hình, sử dụng các công thức toán học. Cách giải: Ta có: 2 2 2 2
AM = AB + BM = 12 + 5 = 13cm
Xét điểm M trên Bx là cực tiểu giao thoa gần B nhất, có: æ 1 ö
AM - BM = k + l ç ÷ è 2 ø æ 1 ö æ 1 ö Û 13 - 5 = k + l Þ k + l = 8cm(1) ç ÷ ç ÷ è 2 ø è 2 ø
Xét điểm N trên AB thuộc cực tiểu giao thoa cùng dãy với M, có: æ 1 ö
AN - BN = k + l = 8cm(2) ç ÷ è 2 ø
Mà: AN - BN = (AO + ON) - (OB -ON) = 2.ON(3)
Từ (2) và (3) Þ 2.ON = 8cm Þ ON = 4cm AB 12 Þ NB = - ON = - 4 = 2cm 2 2
Do N thuộc cực tiểu ngoài cùng nên: l NB <
Þ l2.NB Þ l > 4cm(4) 2 Trang 6 æ 1 ö ék = 0 (loai ) Từ (1) và (4) Þ k + < 2 Þ ç ÷ è 2 ê ø ëk = 1 8 8 16 Þ l = = = cm 1 1 3 k + 1+ 2 2
Gọi C là cực đại xa B nhất → C thuộc cực đại ứng với k = 1 Ta có: 2 2
AC - BC = l Û AB + BC - BC = l 2 2 16
Û 12 + BC - BC = Þ BC = 10,83cm 3
Þl = BC - BM =10,83-5 = 5,83cm Chọn C. Câu 6 (NB): Phương pháp:
Cơ năng, thế năng, động năng của con lắc lò xo dao động điều hòa: 1 1 1 2 2 2
W = kA ;W = kx ;W = mv 2 t 2 d 2 Cách giải: 2 kx
Thế năng của con lắc lò xo khi vật có li độ x là: W = t 2 Chọn C. Câu 7 (VDC): Phương pháp:
Khai thác thông tin từ đồ thị và sử dụng VTLG xác định phương trình li độ: x = A×cos( t w +j) Gia tốc: 2 a = w - x Cách giải:
Ta có: t - t = 0,5s Þtrên Ot mỗi khoảng tương ứng với 0,5s 2 1
Pha của dao động: j = (wt +j0 ) 2p + Khi t = 0 Þ j = - 3 2p 2p Þ w.0 +j = - Þ j = - 0 0 3 3 2p + Khi t t 1s j 0 w æ ö = = Þ = Þ .1+ - = 0 2 ç ÷ è 3 ø 2p æ 2p 2p ö Þ w =
rad / s Þ T = 3s x = Accos ×t - cm ç ÷ 3 è 3 3 ø Phương trình dao động: ì 2p t = t Þ j = ï 3 ï 2p + Khi 3 í
Þ Góc quét tương ứng: Δj = 4p 3 t ï = t Þ j = 4 ïî 3 Trang 7
Vì t - t =1s < T ÞVị trí ứng với 3tvà 4tđược biểu diễn trên đường tròn: 4 3
Quãng đường chất điểm đi được từ thời điểm t3 đến thời điểm t4 là 10cm
→ Từ VTLG ta tính được: S = A = 10cm
→ Phương trình dao động: Gia tốc của vật là: 2 2p 2p 2p 2 a w æ ö æ ö = - x = - ×10×cos ×t - ç ÷ ç ÷ è 3 ø è 3 3 ø 2 40p æ 2p 2p ö Þ a = - ×cos ×t - ç ÷( 2 cm / s ) 2 » 21,9cm / s 9 è 3 3 ø 2 | Þ a |= 21,9cm / s Chọn B.
Câu 8 (VDC): Phương pháp: S S S S
Số cực đại trên đoạn thẳng nối hai nguồn: 1 2 1 2 - < k < l l Cách giải: 10
O là trung điểm của S S 1 2
Từ hình vẽ ta thấy, để trênΔ1có 7 cực đại thì tại A là cực đại bậc 4 l Þ OA = 4 = 2l 2
Trên Δ2 có 3 cực đại thì tại B là cực đại bậc 2 l Þ OB = 2 = l 2
Khoảng cách giữa Δ1và Δ2 là:
AB = OA + OB Û 9 = 3l Þ l = 3cm
Số cực đại trên đoạn S S bằng số giá trị k nguyên thỏa mãn: 1 2 Trang 8 S S S S 28 28 1 2 1 2 - < k < Û - < k < l l 3 3 Û 9,
- 3 < k < 9,3 Þ k = 9 - ; 8 - ; ; … 9
Có 19 giá trị k nguyên thỏa mãn → Trên đoạn S S có 19 cực đại giao thoa. 1 2 Chọn C. Câu 9 (NB): Phương pháp: 2 2
ìA = A + A + 2A A ×cosΔj 1 2 1 2 ï
Biên độ và pha ban đầu của dao động tổng hợp: í
A ×sinj + A ×sinj 1 1 2 2 tanj = ï
A × cosj + A × cosj î 1 1 2 2 Cách giải:
Pha ban đầu của dao động tổng hợp là:
A ×sinj + A ×sinj 1 1 2 2 tanj =
A × cosj + A × cosj 1 1 2 2 Chọn B. Câu 10 (TH): Phương pháp: 1
Năng lượng của vật dao động điều hòa: 2 2
W = mw A 2 Cách giải: w ì = 10p rad / s
Ta có: x = 2cos10pt(cm) Þ í îA = 2cm = 0,02m
Năng lượng dao động của vật là: 1 2 2 1 2 2
W = mw A = × 0,5× (10p ) × 0,02 = 0,1J 2 2 Chọn D. Câu 11 (NB): Phương pháp:
Biểu thức lực kéo về: 2 F = k - x = m - w x Cách giải:
Khi vật qua vị trí có li độ x thì lực kéo về là: 2 F = m - w x Chọn D. Câu 12 (NB): Phương pháp:
Điều kiện xảy ra hiện tượng cộng hưởng cơ: Tần số của lực cưỡng bức bằng tần số dao động riêng của hệ. Cách giải:
Hiện tượng cộng hưởng cơ học xảy ra khi tần số của lực cưỡng bức bằng tần số dao động riêng của hệ. Chọn D. Câu 13 (TH): Phương pháp:
Sử dụng lí thuyết về dao động cưỡng bức. Trang 9 Cách giải:
f là phát biểu không
Tần số của dao động cưỡng bức bằng tần số của lực cưỡng bức → Tần số dao động là 0 đúng. Chọn A. Câu 14 (TH): Phương pháp:
Công thức tính nhiệt lượng tỏa ra: 2 Q = I Rt Cách giải:
Nhiệt lượng tỏa ra trên vật dẫn đó trong 40s là: 12 2 2
Q = I Rt = 2 × 200 × 40 = 32000J = 32kJ Chọn C. Câu 15 (NB): Phương pháp: 2p
Công thức liên hệ giữa w,T, f là: w = = 2p f T Cách giải:
Mối liên hệ giữa tần số góc ωvà tần số f của một dao động điều hòa là: w = 2p f Chọn C. Câu 16 (VD): Phương pháp:
Sử dụng công thức liên hệ giữa chiều dài và chu kì.
Sử dụng lí thuyết về đồ thị hàm số. Cách giải: l l g Ta có: 2 2 2 T = 2p
Þ T = 4p × Þ l = ×T 2 g g 4p g
Đặt: y = l;a = ; x = T 2 4p g 2 2 Þ l =
×T Þ y = a × x 2 4p
→ Đồ thị biểu diễn mối liên hệ giữa chiều dài l của con lắc và chu kì dao động T của nó là đường parabol. Chọn B. Câu 17 (VD): Phương pháp:
Sử dụng kĩ năng khai thác thông tin từ đồ thị. Cách giải: Từ đồ thị ta có:
l = Δx = 33-9 = 24cm Þ l = 48cm 2 Chọn D. Câu 18 (TH): Phương pháp:
Hai dao động cùng pha: Δj = 2kp Trang 10
Hai dao động ngược pha: Δj = (2k +1)p p
Hai dao động vuông pha: Δj = (2k +1) 2 Cách giải: æ p ö æ 2p ö
Độ lệch pha của hai dao động: Δj = wt + - wt - = p ç ÷ ç ÷ è 3 ø è 3 ø
→ Hai dao động ngược pha. Chọn A. Câu 19 (TH): Phương pháp: g
Tần số góc dao động điều hòa của con lắc đơn: w = l Cách giải:
Con lắc dao động với tần số góc là: g 9,8 w = = » 4,4rad / s l 0,5 Chọn C. Câu 20 (NB): Phương pháp:
Sử dụng định nghĩa bước sóng. Cách giải:
Bước sóng là quãng đường sóng truyền đi được trong thời gian một chu kì. Chọn A. Câu 21 (VD): Phương pháp:
Lực cực đại mà lò xo tác dụng lên vật: F
= k × Δl + A max ( 0 )
Biên độ dao động tổng hợp: 2 2
A = A + A + 2A A × cosΔj 1 2 1 2 Cách giải: ìx = 5 2 cos10 c t m 1 ï Ta có: í æ p ö
x = 5 2 sin10t = 5 2 cos 10t - cm ï 2 ç ÷ î è 2 ø
Biên độ dao động tổng hợp là: 2 2 2 2
A = A + A + 2A A ×cosΔj = (5 2) + (5 2) =10cm = 0,1m 1 2 1 2 g g 10 Ta có: w = Þ Δl = = = 0,1m 0 2 2 Δl w 10 0
Lực cực đại mà lò xo tác dụng lên vật: F
= k × Δl + A = mw × Δl + A =1×10 ×(0,1+ 0,1) = 20N max ( 0 ) 2 ( 0 ) 2 Chọn B. Câu 22 (NB): Phương pháp:
Hai dao động cùng pha: Δj = 2kp Trang 11
Hai dao động ngược pha: Δj = (2k +1)p p
Hai dao động vuông pha: Δj = (2k +1) 2 Cách giải:
Hai dao động ngược pha khi hiệu j -j có giá trị bằng (2n +1)π với n = 0, 1 ± , 2, ± … 2 1 Chọn A. Câu 23 (VD): Phương pháp:
Con lắc có biên độ cực đại khi có cộng hưởng: chu kì của lực cưỡng bức bằng chu kì riêng của con lắc. Cách giải:
Từ đồ thị ta thấy với giá trị f » 6(Hz)con lắc có biên độ cực đại. Khi
đó con lắc dao động cộng hưởng, chu kì của lực cưỡng bức bằng chu kì dao động riêng của con 1 1 lắc là: T = = » 0,167(s) f 6 Chọn D. Câu 24 (VD): Phương pháp: k× | q |
Công thức tính cường độ điện trường: E = 2 er Cách giải: k× | q |
Cường độ điện trường tại M: E = = E M 2 e × AM k× | q |
Cường độ điện trường tại N là: E = N 2 e × AN
Mà: AM = MN Þ AN = 2.AM k× | q | k× | q | E Þ E = = = N 2 2 e ×(2× AM ) 4 ×e × AM 4 Chọn B. Câu 25 (VD): Phương pháp: 4A 2
Tốc độ trung bình của vật dao động điều hòa trong 1 chu kì:: v = = .wA tb T p Cách giải:
Phương trình vận tốc: v = x¢ = w - A×sin(2t +j)
Tại thời điểm t1 có: v = w - A×sin 2t +j 1 ( 1 ) é æ p ö ù
Tại thời điểm t2 có: v = w - A×sin 2 t + +j 2 ê ç 1 ÷ ë 4 ú è ø û æ p ö Þ v = w - A×sin 2t +j + 2 ç 1 ÷ è 2 ø Trang 12 2 2 v v 1 2 Þ v ^ v Þ + = 1 1 2 2 2 2 2 w A w A 2 2 2 2
Þ wA = v + v = 5 +12 = 13(cm / s) 1 2 4A 2 2
Tốc độ trung bình của vật trong 1 chu kì: v =
= .wA = .13 » 8,28cm / s tb T p p Chọn C. Câu 26 (NB): Phương pháp: k 1 k m
Tần số góc, tần số, chu kì dao động điều hòa của con lắc lò xo: w = ; f = ;T = 2p m 2p m k Cách giải: k
Tần số góc dao động điều hòa của con lắc lò xo: w = m Chọn D. Câu 27 (TH): Phương pháp: l
Chu kì dao động của con lắc đơn: T = 2p g Cách giải: 2 l 4p l Ta có:T = 2p Þ g = 2 g T
Sử dụng đồng hồ đo được T, dùng thước đo được l → xác định được gia tốc trọng trường. Chọn D. Câu 28 (NB): Phương pháp:
Sử dụng lí thuyết về dao động tắt dần. Cách giải:
Dao động tắt dần có biên độ và năng lượng giảm dần theo thời gian. Chọn D. Câu 29 (VD): Phương pháp: 1 1 1
Cơ năng của con lắc lò xo dao động điều hòa: 2 2 2
W = W +W Û kA = kx + mv t d 2 2 2 Cách giải:
Ta có: W = W +W t d 2 k ×0
VTCB có x = 0 Þ W = = 0 t 2 1 2
Þ W = 0 +W Û kA = 0,5 d 2 2.0,5 1 Þ A = = = 0,1m = 10cm k 100 Chọn A. Trang 13 Câu 30 (NB): Phương pháp:
Công thức tính công nguồn điện sinh ra: A It = ξ Cách giải:
Trong thời gian t, công mà nguồn điện sinh ra bằng ξ It Chọn A. Câu 31 (NB): Phương pháp:
Sử dụng lí thuyết về phương trình sóng. Cách giải:
Phương trình sóng tại nguồn: u = Acos t w 0 æ 2p x ö
Phương trình dao động tại điểm M cách nguồn một khoảng x là: u = Acos wt - M ç l ÷ è ø Chọn D. Câu 32 (TH): Phương pháp: 1
Công thức tính thế năng: 2 2
W = mw x t 2 Cách giải: 1 Thế năng: 2 2
W = mw x t 2 1 Khi 2 2
x = A Þ W = mw A t 2 Chọn C. Câu 33 (VD): Phương pháp: l
Chu kì dao động của con lắc đơn: T = 2p g Cách giải: l Ta có: T = 2p g 2 2 T × g 2 ×9,81 Þ l = = = 0,99396(m) 2 2 4p 4p Chọn D. Câu 34 (VD): Phương pháp: Tốc độ của vật: 2 2
v = w A - x Cách giải: æ p ö ìA = 5cm
Ta có: x = 5cos 10t + (cm) Þ ç ÷ í è 6 ø w î =10rad / s
Khi x = 2,5 cm thì tốc độ của vật là: 2 2 2 2
v = w A - x =10 5 - 2,5 = 25 3cm / s Trang 14 Chọn C. Câu 35 (TH): Phương pháp:
Sử dụng lí thuyết về các loại dao động. Cách giải:
Hệ thống giảm xóc ở ô tô là ứng dụng của dao động tắt dần. Chọn B. Câu 36 (VDC): Phương pháp:
ìx = A cos( t w )
Phương trình dao động của hai chất điểm: 1 1 í
x = A cos( t w + Δj) î 2 2
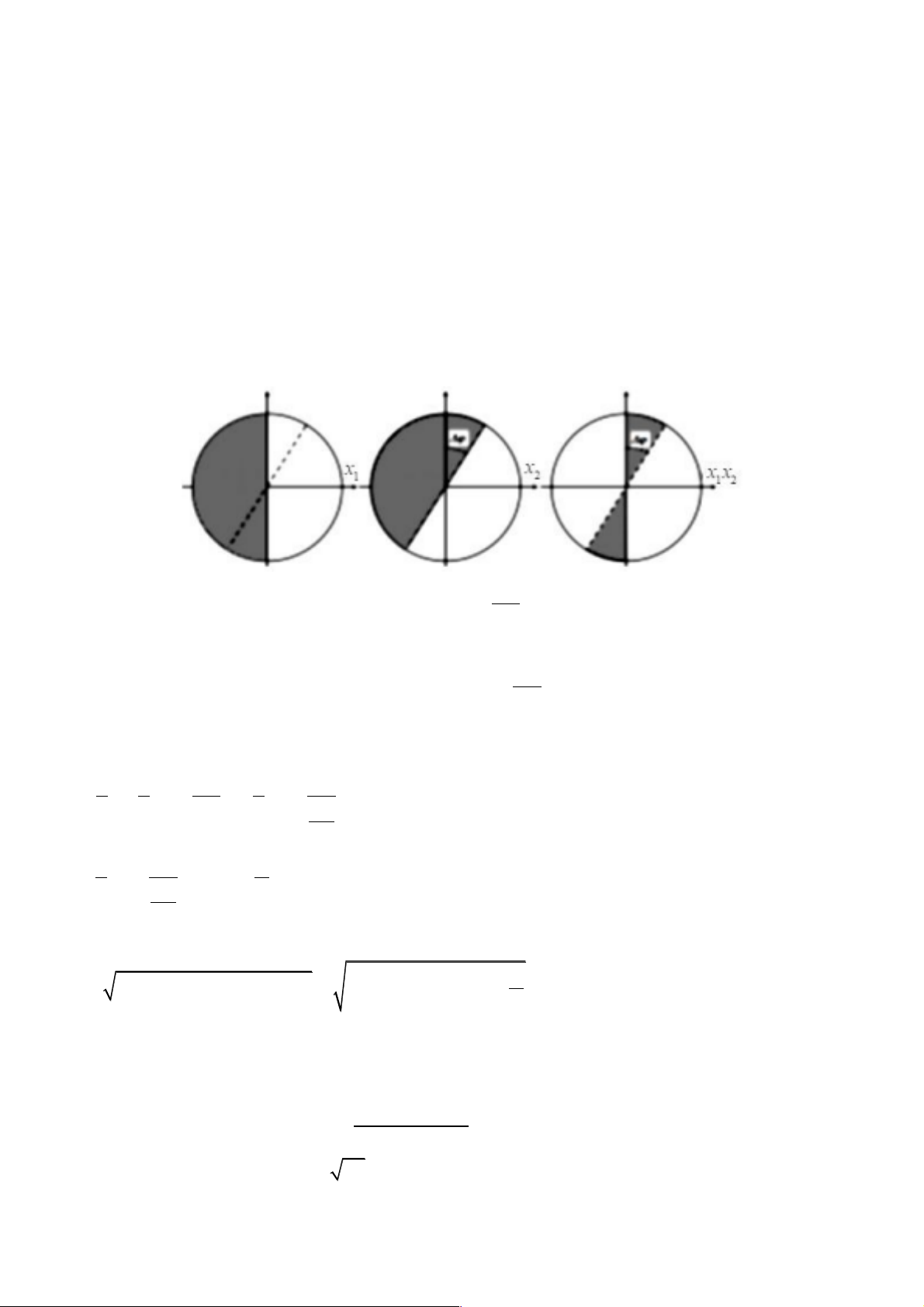
Dấu của x , x và x x được biểu diễn như trên hình vẽ: 1 2 1 2 Δj
Khoảng thời gian trong 1 chu kì để x x < 0 là t = 2 × 1 2 w Cách giải: Δj
Khoảng thời gian trong một chu kì để x x < 0 là t = 2 × 1 2 w
Với Δϕ là độ lệch pha của hai dao động. Theo đề bài ta có: 2 2 Δj 2 Δj t = Þ = 2× Û = 2× 3 3 w 3 2p T 2 Δj p Û = 2× Þ Δj = 3 2p 3 2
Biên độ dao động tổng hợp là: p 2 2 2 2
A = A + A + 2A A × cosΔj = 3 + 4 + 2 ×3× 4 × cos » 6,1cm 1 2 1 2 3 Chọn B. Câu 37 (VDC): Phương pháp: tan a - tan b
Công thức lượng giác: tan(a - b) =
1+ tan a × tan b
Bất đẳng thức Cô – si: a + b ³ 2 ab (dấu “=” xảy ra ⇔ a = b)
Điều kiện cực đại giao thoa: d - d = kl 2 1 Trang 15 æ 1 ö
Điều kiện cực tiểu giao thoa: d - d = k + l 2 1 ç ÷ è 2 ø Cách giải: 19 Ta có: PO Q = j -j 2 2 1 tanj - tanj
Þ tan PO Q = tan j -j = 2 ( 2 1) 2 1 1+ tanj × tanj 2 1 O Q O P 1 1 O Q O P - 1 1 - O O O O Þ tan ( a a j -j = = 2 1 ) 1 2 1 2 O Q O P O Q O P 1 1 1 1 1+ × 1+ × O O O O a a 1 2 1 2 O Q O P PQ tan (j j - Þ - = = 2 1 ) 1 1 O . Q O P O . Q O P 1 1 1 1 a + a + a a O . Q O P Để tan (j j æ ö - Û a + 2 1 ) 1 1 max ç ÷ è a ømin
Áp dụng bất đẳng thức Cô – si, ta có: O Q ×O P O Q ×O P 1 1 1 1 a + ³ 2 a × a a æ O Q ×O P ö 1 1 Þ a + = 2 O Q ×O P ç ÷ 1 1 è a ømin
(Dấu “=” xảy ra Û a = O . Q O P = 4,5.8 = 6(cm)) 1 1 Ta có: 2 2 2 2
O P = a + O P = 6 + 4,5 = 7,5(cm) 2 1 Lại có: 2 2 2 2
O Q = a + O Q = 6 + 8 = 10(cm) 2 1 æ 1 ö
Điểm P không dao động, ta có: PO - PO = 7,5 - 4,5 = k + l 2 1 ç ÷ è 2 ø
Điểm Q dao động với biên độ cực đại: QO - QO =10 - 8 = kl 2 1 Ta có hệ phương trình: ì 1 3 ï = (k + )l ìk = 1 í 2 Þ í ï îl = 2(cm) î2 = kl
→ Q là cực đại bậc 1, giữa P và Q không có cực đại nào khác. Trang 16
Trên OP, gọi N là điểm gần nhất dao động với biên độ cực đại → N là cực đại bậc 2 ứng với k = 2, ta có: 2 2
ON + a - ON = 2l 2 2
Þ ON + 6 -ON = 2.2 Þ ON = 2,5(cm)
Þ PN = O P - ON = 4,5 - 2,5 = 2(cm) 1 Chọn C. Câu 38 (NB): Phương pháp:
Trong giao thoa sóng hai nguồn cùng pha:
+ Điều kiện có cực đại giao thoa: d - d = kl 2 1 æ 1 ö
+ Điều kiện có cực tiểu giao thoa: d - d = k + l 2 1 ç ÷ è 2 ø Cách giải:
Trong giao giao thoa sóng hai nguồn cùng pha, những điểm dao động với biên độ cực đại có hiệu
khoảng cách tới hai nguồn là kλ . Chọn D. Câu 39 (TH): Phương pháp:
Công thức tính lực kéo về: 2
P = -mw × s t Cách giải:
Biểu thức xác định lực kéo về: 2 P = m - w s t ì g w ï = g Với: í
l Þ P = -m × ×a ×l = -mga t l ïîs =a ×l Chọn C. Câu 40 (NB): Phương pháp:
Phương trình dao động điều hòa: x = Acos( t w +j)
Trong đó: x là li độ của dao động; A là biên độ dao động; ωlà tần số góc; ϕlà pha ban đầu; ( t
w +j)là pha của dao động. Cách giải:
Đại lượng ωtrong phương trình x = Acos( t
w +j)được gọi là tần số góc của dao động. Chọn D. Trang 17