Đề thi thử tốt nghiệp THPT 2025 môn Toán bám sát đề minh họa - Đề 33
Lễ kỷ niệm 30 năm thành lập trường THPT Chu Văn An – Biên Hòa (1994-2024), nhà trường có cho dựng 1 cổng chào hình parabol với điểm cao nhất là 6m và khoảng cách giữa hai chân cổng chào là 8m. Hỏi diện tích của cổng chào là bao nhiêu mét vuông? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2022 75 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
ĐỀ ÔN THI TỐT NGHIỆP THPT 2025 ĐỀ 33 MÔN: TOÁN Thời gian: 90 phút
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1.
Họ tất cả các nguyên hàm của hàm số f x sin 2x là 1 1
A. cos 2x C .
B. cos 2x C . C.
cos 2x C .
D. cos 2x C . 2 2 Câu 2.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y e và các đường thẳng y 0 , x 0 , x 2 bằng 2 2 2 2 A. x e dx . B. 2 x e dx . C. 2 x e dx . D. x e dx . 0 0 0 0 Câu 3.
Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một
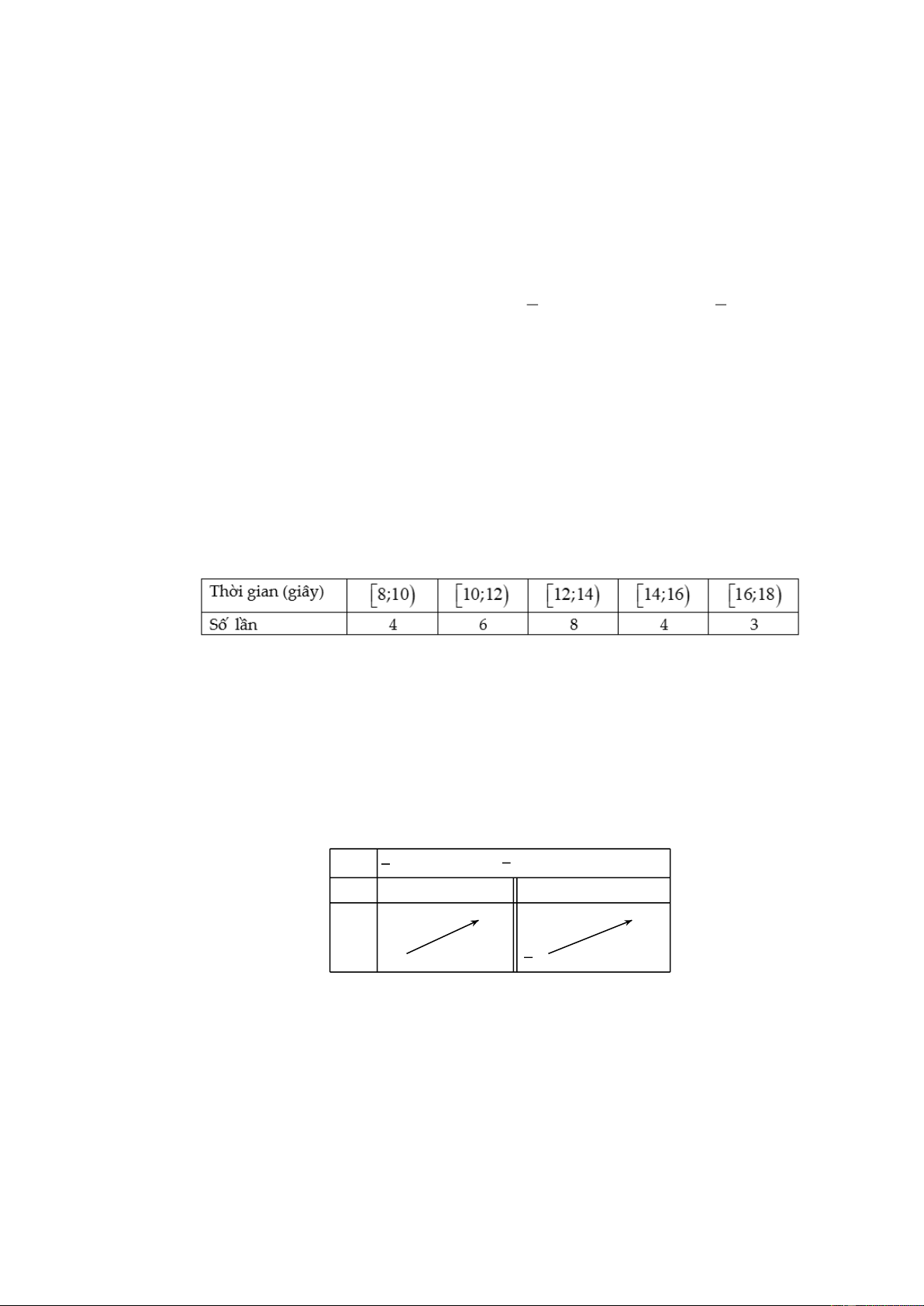
lần tập luyện giải khối rubik 3×3, bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần
giải liên tiếp ở bảng sau:
Độ lệch chuẩn của mẫu số liệu nêu trên gần với giá trị nào sau đây nhất? A. 5,98. B. 6. C. 2,44. D. 2,5. Câu 4.
Trong hệ tọa độ Oxyz, phương trình nào sau đây là phương trình mặt phẳng Oyz ?
A. x y 0 .
B. z 0.
C. x 0 . D. y 0 . Câu 5.
Cho hàm số f xcó bảng biến thiên: x ∞ 1 +∞ y' + + +∞ +∞ y 2 ∞
Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số? A. x 1 . B. y 1 .
C. y 2 . D. x 2 . Câu 6.
Tìm tập nghiệm của bất phương trình 2x x6 2 2 . A. ;6 .
B. 0; . C. 0; 1 . D. 1; . x 1 Câu 7.
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : y 2 3t ; t . Véctơ chỉ z 5t
phương của d là: A. u 0;3; 1 B. u 1;3; 1 C. u 1; 3 ; 1 D. u 1; 2;5 4 3 2 1 Câu 8.
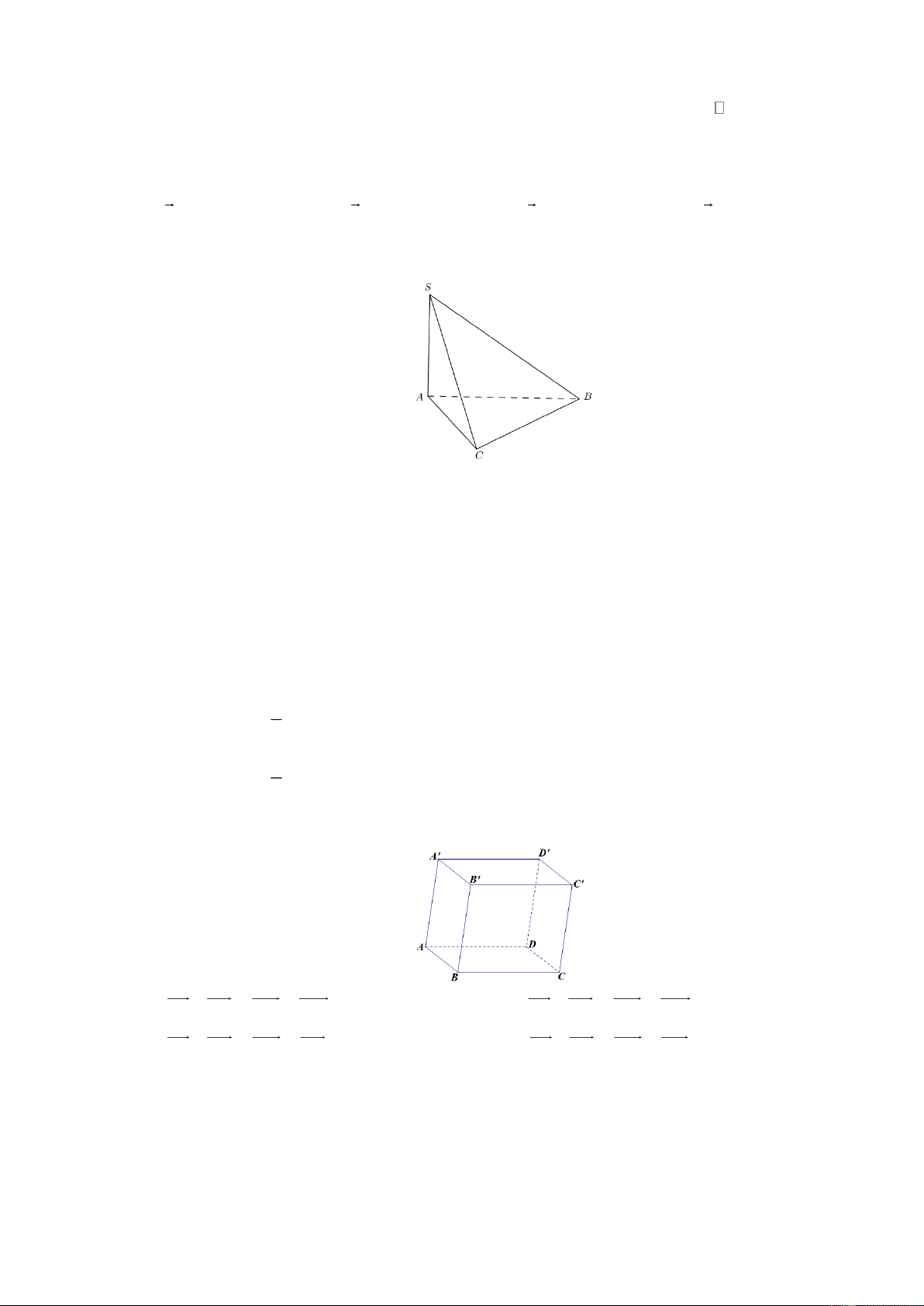
Cho hình chóp S.ABC (như hình vẽ) có SA ABC , góc giữa SB và mặt phẳng ABC là A. SBA . B. SAB . C. SBC . D. SCB . Câu 9.
Nghiệm của phương trình logx 1 0 là
A. x 11.
B. x 10 .
C. x 2 . D. x 1.
Câu 10. Cho dãy số 729, 486, 324, 216,144, 96, 64,... là một cấp số nhân với:
A. Công bội q 3 .
B. Công bội q 2 . C. Công bội 2 q . 3 D. Công bội 1 q . 2
Câu 11. Cho hình hộp ABC .
D A' B 'C ' D' . Đẳng thức nào sau đây là đẳng thức đúng?
A. BA BC BB ' BC ' .
B. BA BC BB ' BD ' .
C. BA BC BB ' BD .
D. BA BC BB ' BA' .
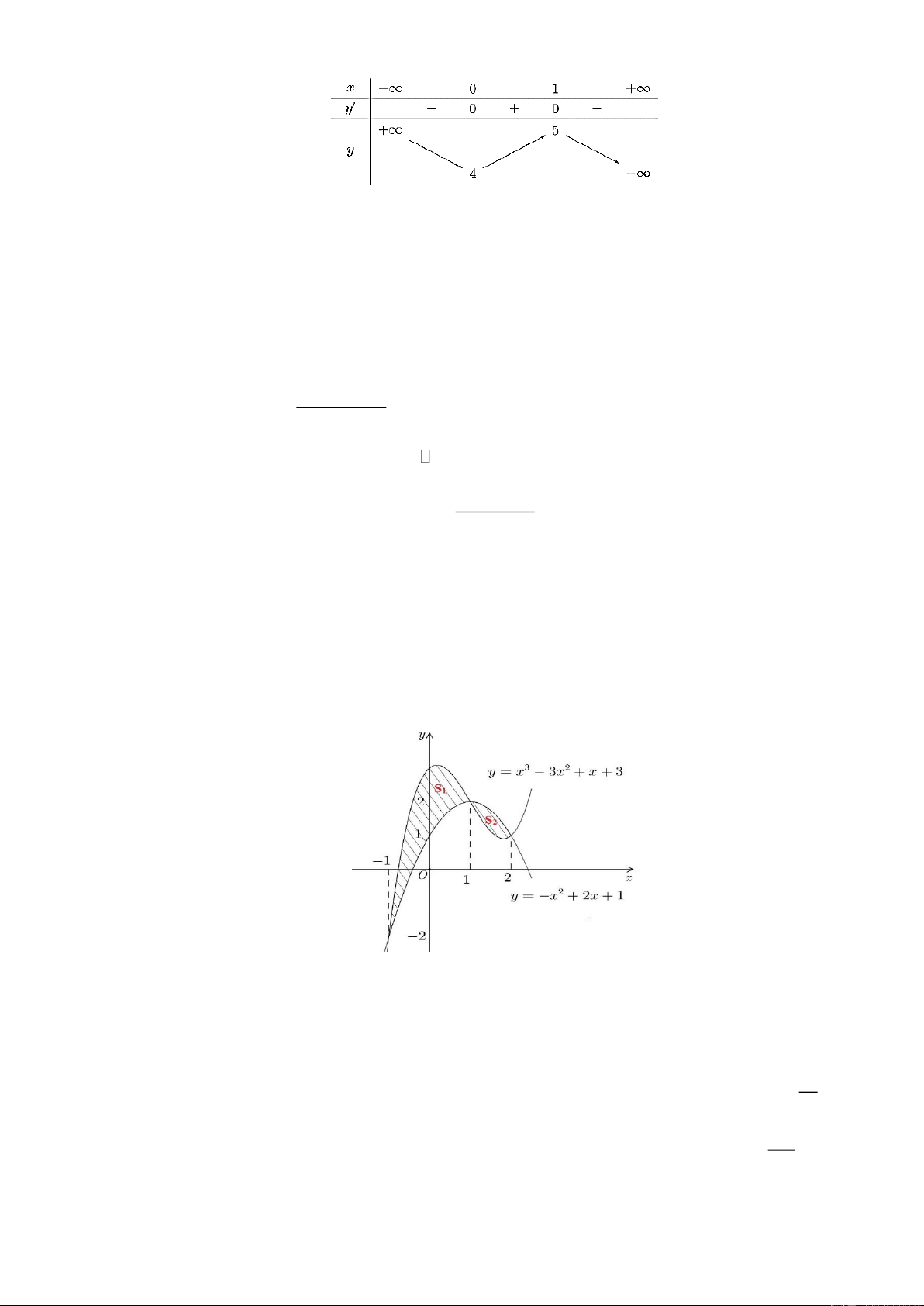
Câu 12. Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây
Hàm số đã cho nghịch biến trên khoảng
A. 0; .
B. ;0 . C. 0; 1 . D. ;5 .
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. x x Câu 1.
Cho hàm số f x 2 2 6 . x 1
a) Tập xác định của hàm số f x là . 2
b) Đạo hàm của hàm số x 2x 8
f x là f x . x 2 1
c) Giá trị cực đại của hàm số f x bằng 2.
d) Giá trị nhỏ nhất của hàm số y f x trên 4 ; 2 là 10. Câu 2. Cho hàm số 3 2
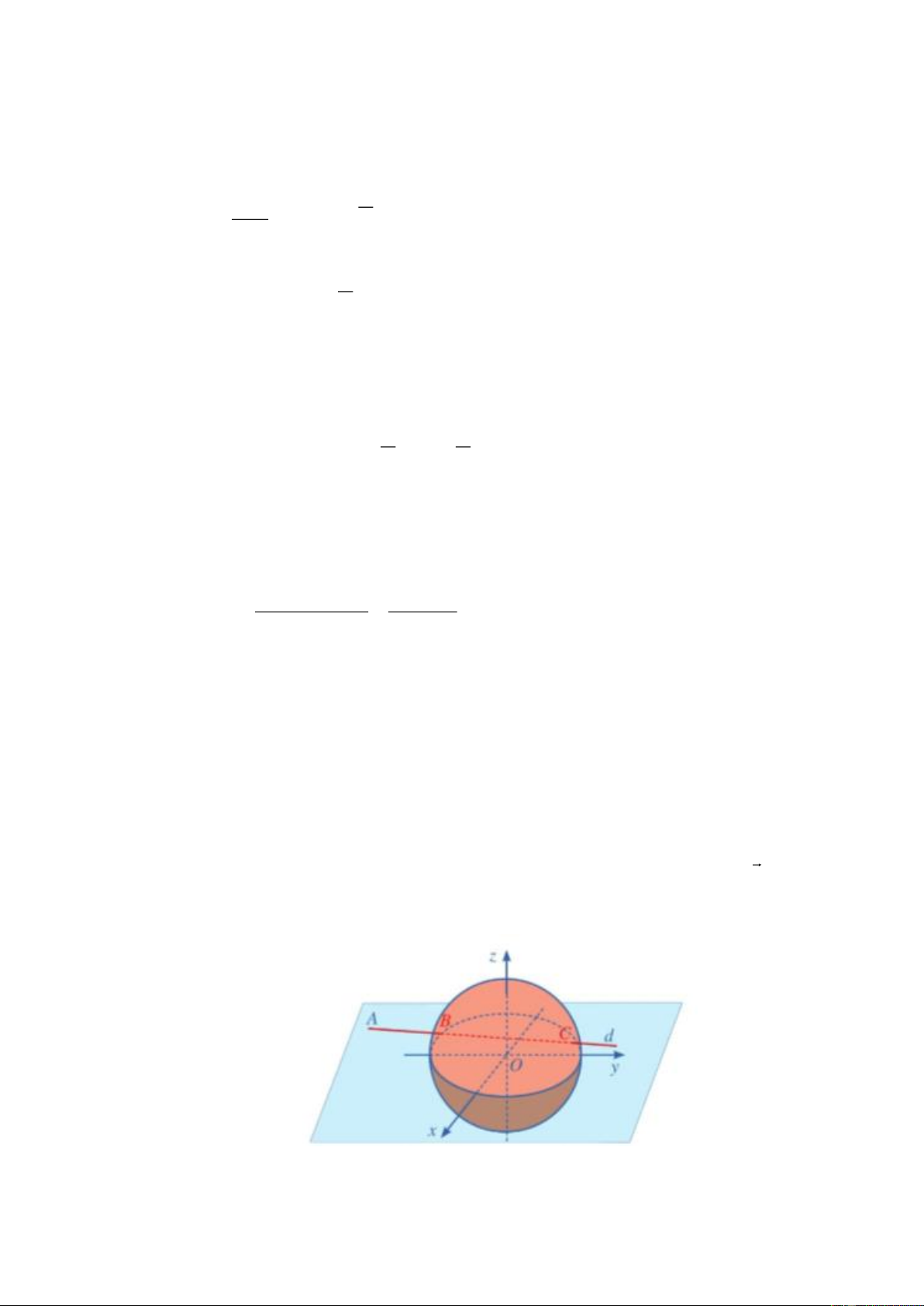
y x 3x x 3 có đồ thị là P và 2
y x 2x 1 có đồ thị là H . Gọi
S , S là diện tích hình phẳng giới hạn bởi đồ thị P và H như hình vẽ. 1 2 2
a) Diện tích phần hình phẳng E được gạch sọc tính theo công thức 3 2
x 2x x 2dx 1 b) S 3S . 1 2
c) Diện tích hình phẳng giới hạn bởi 10
H , trục hoành và hai đường thẳng x 0, x 2 là . 3
d) Khi quay hình phẳng E quanh trục Ox ta được khối tròn xoay có thể tích 185 V . 21 Câu 3.
Một trường năng khiếu có 1000 học sinh. Trong đó có 200 học sinh tham gia câu lạc bộ âm
nhạc, và có 85% học sinh biết chơi đàn guitar. Ngoài ra, có 10% số học sinh không tham gia
câu lạc bộ âm nhạc cũng biết chơi đàn guitar. Chọn ngẫu nhiên 1 học sinh của trường.
a) Xác suất chọn được học sinh không tham gia câu lạc bộ âm nhạc là 0,9.
b) Xác suất chọn được học sinh vừa tham gia câu lạc bộ âm nhạc vừa biết chơi đàn ghi ta là 0,17.
c) Xác suất chọn được học sinh biết chơi đàn ghi ta là 0, 25.
d) Giả sử học sinh đó biết chơi đàn guitar. Xác suất chọn được học sinh thuộc câu lạc bộ âm nhạc là 0, 7 . Câu 4.
Hệ thống Kiểm soát không lưu, còn gọi là kiểm soát không lưu (tiếng anh: air traffic control,
viết tắt là ATC), hay Điều khiển không lưu là hệ thống chuyên trách đảm nhận việc gửi các
hướng dẫn đến máy bay nhằm giúp các máy bay tránh va chạm, đồng thời đảm bảo tính hoạt
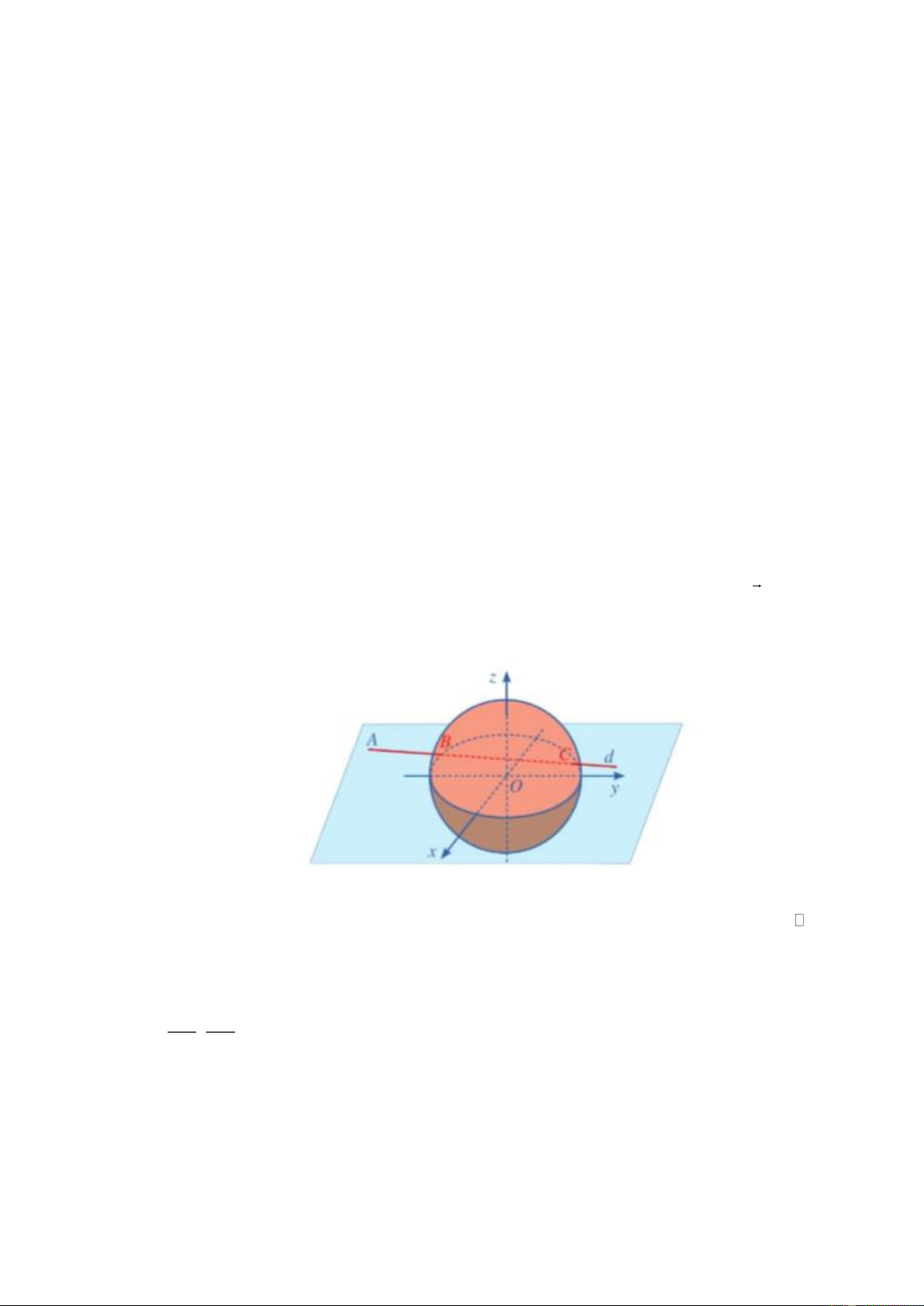
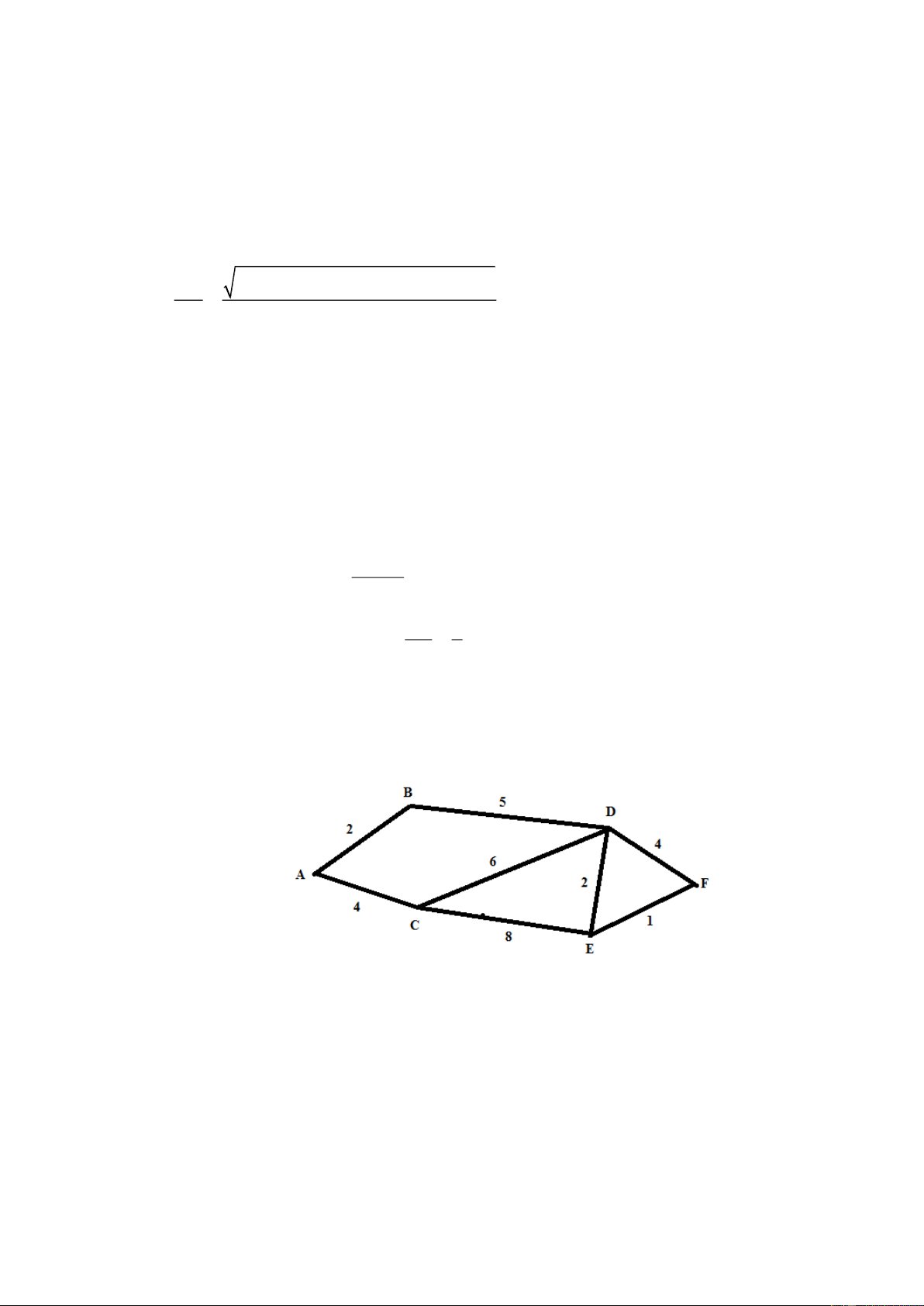
động hiệu quả của nền tảng không lưu. Trong không gian với hệ tọa độ Oxyz , xét một đài kiểm
soát không lưu sân bay có tọa độ O0;0;0 , mỗi đơn vị trên trục ứng với 1 km. Máy bay bay
trong phạm vi cách đài kiểm soát 417 km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A 6
88;185;8chuyển động theo đường thẳng d có vectơ chỉ phương là u 91;75;0
và hướng về đài kiểm soát không lưu (Hình hình mô tả dưới). x 6 88 91t
a) Phương trình đường thẳng mô tả đường bay của máy bay trên là y 1
85 75t ,t . z 8
b) Xác định tọa độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất là điểm 375 455 ; ;8 . 2 2
c) Vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa có tọa độ 8 8;415;8 .
d) Giả sử suốt quá trình được theo dõi bở đài kiểm soát không lưu này máy bay luôn giữ vận
tốc không đổi là 800 km / h thì mất 0, 62 giờ (làm tròn đến hàng phần trăm)?
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
PHẦN III: TRẢ LỜI NGẮN Câu 1.
Cho hình chóp S.ABC có thể tích bằng 3
20a và diện tích tam giác ABC là 2 10a . Biết
SC 12 a . Tính số đo góc tạo giữa đường thẳng SC và ABC . Câu 2.
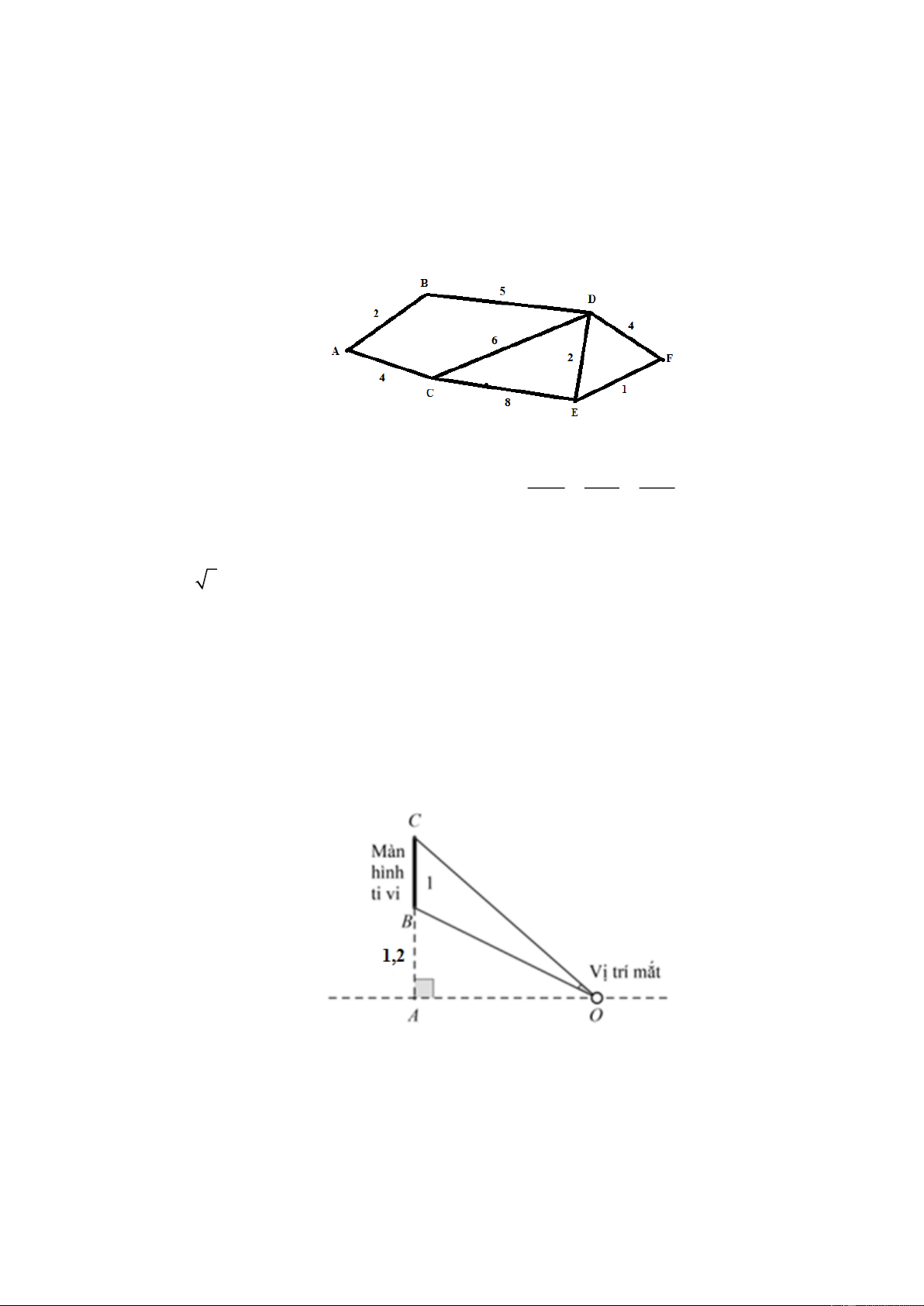
Trong 1 trò chơi thực tế, người ta thiết kế, bố trí số lượng cạm bẫy cho người chơi phải gặp trên
đoạn đường đi như mô tả trên hình. Người chơi sẽ xuất phát từ điểm A và về đích ở điểm F .
Hãy cho biết số cạm bẫy cần vượt qua ít nhất là bao nhiêu khi người chơi về tới đích. x y z Câu 3.
Trong không gian Oxyz , cho đường thẳng d 2 1 5 : và 2 điểm A 2 ;1; 1 , 1 3 2 B 3 ; 1
;2 . Điểm M ; a ;
b c (với c 0 ) thuộc đường thẳng d sao cho MA B có diện tích
bằng 3 5 . Khi đó, tổng a + b + c bằng bao nhiêu ? Câu 4.
Lễ kỷ niệm 30 năm thành lập trường THPT Chu Văn An – Biên Hòa (1994-2024), nhà trường
có cho dựng 1 cổng chào hình parabol với điểm cao nhất là 6m và khoảng cách giữa hai chân
cổng chào là 8m . Hỏi diện tích của cổng chào là bao nhiêu mét vuông ? Câu 5.
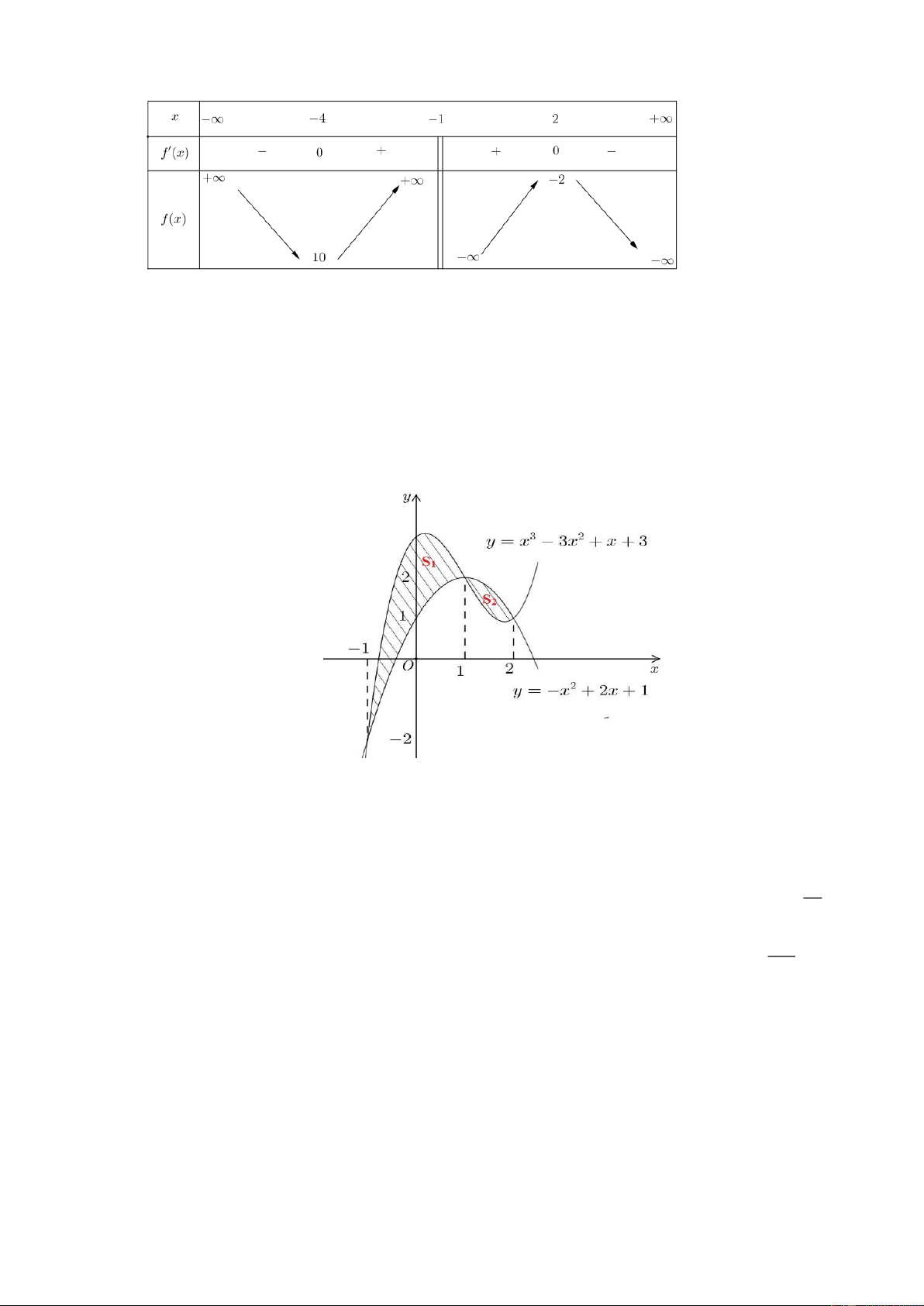
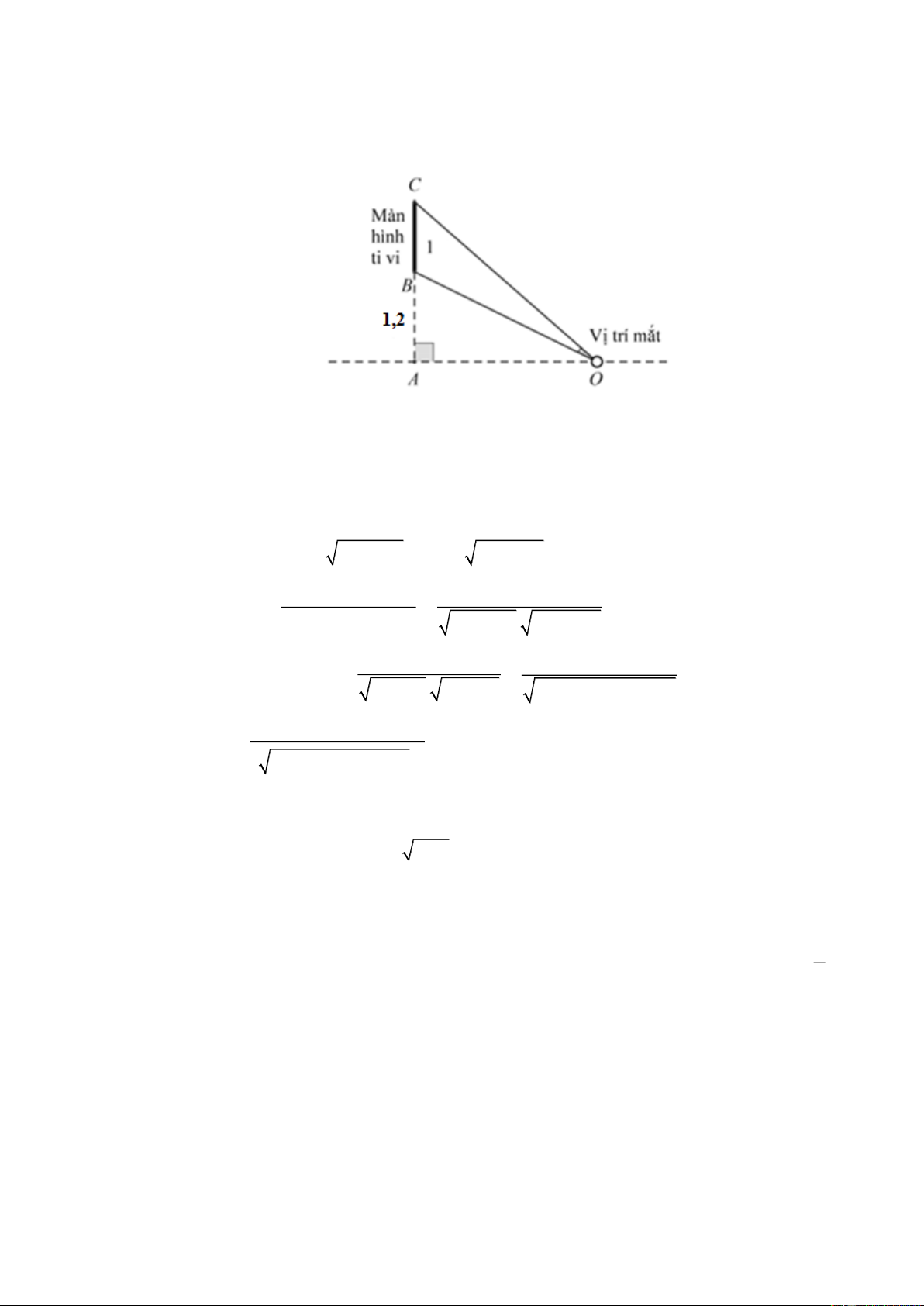
Trong lớp học, màn hình tivi hình chữ nhật có chiều cao 1m được đặt ở độ cao 1, 2m so với tầm
mắt của học sinh (tính từ đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí ngồi
sao cho góc nhìn lớn nhất ( BOC là góc nhìn).
Nếu xét học sinh Nam ngồi nhìn thẳng màn hình thì học sinh Nam ngồi bàn thứ mấy nhìn được
rõ nhất, biết vị trí ngồi bàn đầu tiên cách tivi 1, 2m và mỗi bàn kế tiếp nhau cách nhau 0,4m (giả
sử khoảng cách các bàn như nhau). Câu 6.
Gọi S là tập hợp các số tự nhiên có ba chữ số phân biệt lấy từ các chữ số 1;2;3;4;5;6;7 . Chọn
ngẫu nhiên một số từ S . Biết rằng xác suất chọn được số chẵn là phân số tối giản a , hãy tính b a b . HẾT ĐÁP ÁN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn D D C C A A A A C C B B
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Thí sinh chỉ lựa chọn chính xác 01 ý trong 01 câu hỏi được 0,1 điểm;
Thí sinh chỉ lựa chọn chính xác 02 ý trong 01 câu hỏi được 0,25 điểm;
Thí sinh chỉ lựa chọn chính xác 03 ý trong 01 câu hỏi được 0,5 điểm;
Thí sinh lựa chọn chính xác cả 04 ý trong 01 câu hỏi được 1 điểm. Câu 1 2 3 4 a) Sai a) Sai a) Sai a) Đúng b) Đúng b) Đúng b) Đúng b) Đúng Đáp án c) Sai c) Đúng c) Đúng c) Sai d) Sai d) Đúng d) Sai d) Đúng
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.Mỗi câu trả lời đúng thí sinh được 0,5 điểm. Câu 1 2 3 4 5 6 Đáp án 30 10 -30 32 2 10
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Lời giải Chọn D 1
Ta có: sin 2xdx cos 2x C . 2 Câu 2. Lời giải Chọn D Ta có x e 0, x 0; 2 .
Do đó diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y e và các đường thẳng y 0 , x 0 , 2 x 2 là x
S e dx . 0 Câu 3. Lời giải Chọn C
4.9 6.11 8.13 4.15 3.17 Ta có x 12,68 . 25 1 s
4.9 x 2 6.11 x 2 8.13 x 2 4.15 x 2 3.17 x 2 2 5,9776 25 . s 2, 44 . Câu 4. Lời giải Chọn C
Mặt phẳng Oyz có phương trình là x 0 . Câu 5. Lời giải Chọn A
Vì lim y ; lim y nên đồ thị hàm số đã cho nhận đường thẳng x 1 làm tiệm cận x 1 x 1 đứng. Câu 6. Lời giải Chọn A Ta có: 2x x6 2 2
2x x 6 x 6.
Vậy tập nghiệm của bất phương trình đã cho là ;6 . Câu 7. Lời giải Chọn A x 1
Đường thẳng d : y 2 3t ; (t ) nhận véc tơ u 0;3; 1 làm VTCP z 5t Câu 8. Lời giải Chọn A
Vì SA ABC nên hình chiếu của SB lên ABC là AB SB; ABC SBA . Câu 9. Lời giải Chọn C x 0 log
1 0 x 1 10 x 2 . Câu 10. Lời giải Chọn C u 2 Ta có: u 729 , 2
u 486 q . 1 2 u 3 1
Vậy dãy số đã cho là cấp số nhân với công bội 2 q
và số hạng đầu là u 729 . 3 1 Câu 11. Lời giải Chọn B
Áp dụng quy tắc hình bình hành ta có: BA BC BD .
Suy ra BA BC BB ' BD BB ' BD ' . Câu 12. Lời giải Chọn B
Dựa vào BBT, ta thấy hàm số đã cho nghịch biến trên các khoảng ;0
và 1;.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. x x Câu 1.
Cho hàm số f x 2 2 6 . x 1
a) Tập xác định của hàm số f x là . 2
b) Đạo hàm của hàm số x 2x 8
f x là f x . x 2 1
c) Giá trị cực đại của hàm số f x bằng 2.
d) Giá trị nhỏ nhất của hàm số y f x trên 4 ; 2 là 10. Lời giải a) Sai.
Hàm số f x 2 x 2x 6
xác định khi x 1 0 x 1 . x 1
Do đó hàm số f x có tập xác định là \ 1 . b) Đúng. 2
x 2x 6 x 1 2
x 2x 6x f x 2 1 x 2x 8 . x 1 x 2 1 c) Sai. f x 2 x 2x 8 x 2 2 0 . x 0 x 2x 8 0 2 1 x 4 Bảng biến thiên:
Vậy hàm số f x có giá trị cực đại bằng 2 . d) Sai. Trên 4 ;
2 , hàm số không có giá trị nhỏ nhất. Câu 2. Cho hàm số 3 2
y x 3x x 3 có đồ thị là P và 2
y x 2x 1 có đồ thị là H . Gọi
S , S là diện tích hình phẳng giới hạn bởi đồ thị P và H như hình vẽ. 1 2 2
a) Diện tích phần hình phẳng E được gạch sọc tính theo công thức 3 2
x 2x x 2dx 1 b) S 3S . 1 2
c) Diện tích hình phẳng giới hạn bởi 10
H , trục hoành và hai đường thẳng x 0, x 2 là . 3
d) Khi quay hình phẳng E quanh trục Ox ta được khối tròn xoay có thể tích 185 V . 21 Lời giải a) Sai
+ Phần S : phần diện tích hình phẳng giới hạn bởi các đồ thị hàm số 1 f x 3 2
x 3x x 3, g x 2
x 2x 1 và các đường thẳng x 1 , x 1.
+ Phần S : phần diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 f x 3 2
x 3x x 3, g x 2
x 2x 1và các đường thẳng x 1, x 2 . 1 2
Do đó: S S S 3 2
x 2x x 2 dx 3 2
x 2x x 2dx . 1 2 1 1 1 2
Vậy S S S 3 2
x 2x x 2 dx 3 2
x 2x x 2dx . 1 2 1 1 b) Đúng 1 1 8 S
f x g x dx 3 2
x 2x x 2dx . 1 3 1 1 2 2 5
S g x f x dx 3 2
x 2x x 2dx . 2 12 1 1 Do đó: 32 S S . 1 2 5 c) Đúng 2 2 S g
xdx 10 2
x 2x 1 dx . 3 0 0 d) Đúng
Gọi V ,V lần lượt là thể tích khối tròn xoay khi quay hình phẳng E quanh trục Ox với 1 2
các đường thẳng x 1
; x 1 và x 2 . 1 160 +) 2 V f x 2 g x d x ; 1 21 1 2 25 +) 2 V g x 2 f x dx . 2 21 1 Vậy 185
V V V . 1 2 21 Câu 3.
Một trường năng khiếu có 1000 học sinh, trong đó có 200 học sinh tham gia câu lạc bộ âm
nhạc, trong số học sinh đó có 85% học sinh biết chơi đàn guitar. Ngoài ra, có 10% số học sinh
không tham gia câu lạc bộ âm nhạc cũng biết chơi đàn guitar. Chọn ngẫu nhiên 1 học sinh của trường.
a) Xác suất chọn được học sinh không tham gia câu lạc bộ âm nhạc là 0,9.
b) Xác suất chọn được học sinh vừa tham gia câu lạc bộ âm nhạc vừa biết chơi đàn ghi ta là 0,17.
c) Xác suất chọn được học sinh biết chơi đàn ghi ta là 0, 25.
d) Giả sử học sinh đó biết chơi đàn guitar. Xác suất chọn được học sinh thuộc câu lạc bộ âm nhạc là 0, 7 . Lời giải
Xét các biến cố: A : "Chọn được học sinh thuộc câu lạc bộ âm nhạc";
B : "Chọn được học sinh sinh biết chơi đàn guitar”; a) Sai A 200 P
0, 2 P A 0,8. 1000 b) Đúng
P B∣ A 0,85; P B∣ A 0,1. Xác suất cần tìm là P AB ta có theo công thức nhân xác
suất P AB PB A P A .PB∣
A 0, 2.0,85 0,17 . c) Đúng
Theo công thức xác suất toàn phần, ta có:
P B P A P B∣ A P A PB∣ A 0,20,85 0,80,1 0,25 . d) Sai
Theo công thức Bayes, xác suất chọn được học sinh thuộc câu lạc bộ âm nhạc, biết học sinh
đó chơi được đàn guitar, là: ∣ A∣ B
P A P B A 0, 2 0,85 P . Mệnh đề sai. B 0, 68 P 0, 25 Câu 4.
Hệ thống Kiểm soát không lưu, còn gọi là kiểm soát không lưu (tiếng anh: air traffic control,
viết tắt là ATC), hay Điều khiển không lưu là hệ thống chuyên trách đảm nhận việc gửi các
hướng dẫn đến máy bay nhằm giúp các máy bay tránh va chạm, đồng thời đảm bảo tính hoạt
động hiệu quả của nền tảng không lưu. Trong không gian với hệ tọa độ Oxyz , xét một đài kiểm
soát không lưu sân bay có tọa độ O0;0;0 , mỗi đơn vị trên trục ứng với 1 km. Máy bay bay
trong phạm vi cách đài kiểm soát 417 km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A 6
88;185;8chuyển động theo đường thẳng d có vectơ chỉ phương là u 91;75;0
và hướng về đài kiểm soát không lưu (Hình hình mô tả dưới). x 6 88 91t
a) Phương trình đường thẳng mô tả đường bay của máy bay trên là y 1
85 75t ,t . z 8
b) Xác định tọa độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất là điểm 375 455 ; ;8 . 2 2
c) Vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa có tọa độ 8 8;415;8 .
d) Giả sử suốt quá trình được theo dõi bởi đài kiểm soát không lưu này máy bay luôn giữ vận
tốc không đổi là 800 km / h thì mất 0, 62 giờ (làm tròn đến hàng phần trăm)?. Lời giải a) Đúng
Phương trình tham số của đường thẳng d đi qua điểm A 6
88;185;8 và có vectơ chỉ x 6 88 91t
phương u 91;75;0 là: y 1
85 75t (t là tham số). z 8 b) Đúng
Gọi H là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Khi đó, khoảng cách
OH phải ngắn nhất, điều này xảy ra khi và chỉ khi OH d .
Vì H d nên H 6
8891t;185 75t;8 . Ta có OH 6
88 91t;185 75t;8.
OH d OH.u 0 6
8891t.91 1
85 75t.758.0 0 13906t 76483 11 0 t 2 Do đó 375 455 H ; ;8 . 2 2 c) Sai
Lưu ý rằng, M bay từ A hướng về ATC khi và chỉ khi t lớn dần từ 0
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vì Bd nên B 6
8891t ;185 75t ;8 .
B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa khi OB 417 . t2 t2 2 688 91 185 75 8 417. 2
13906t 152966t 333744 0 .
t 3 hoặc t 8 (loại t 8)
Với t 3, ta có B 4 15;40;8 . d) Sai
Vị trí đầu tiên và cuối cùng của M trên màn hình ra đa là B 4
15;40;8 vàC40;415;8 .
Do đó thời gian xuất hiện trên màn hình ra đa là BC 2 2 2 40 415 415 40 8 8 0,74 (giờ). 800 800
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1.
Trong không gian, cho hình chóp S.ABC có thể tích bằng 3
20a và diện tích tam giác ABC là 2
10a . Biết SC 12 a . Tính số đo góc tạo giữa đường thẳng SC và ABC . Lời giải Trả lời: 30
Gọi H là hình chiếu của S lên ABC 3V
Ta có: SH d S,(ABC) S . ABC 6 a S ABC SH Ta có: SC SBC 1 sin , ( ) sin SCA SC 2
Vậy góc giữa đường thẳng SC và ABC bằng 300 Câu 2.
Trong 1 trò chơi thực tế, người ta thiết kế, bố trí số lượng cạm bẫy cho người chơi phải gặp trên
đoạn đường đi như mô tả trên hình. Người chơi sẽ xuất phát từ điểm A và về đích ở điểm F .
Hãy cho biết số cạm bẫy cần vượt qua ít nhất là bao nhiêu khi người chơi về tới đích. Lời giải Trả lời: 10
Tính toán các khả năng di chuyển, ta tính được số cạm bẫy ít nhất cần vượt qua là 2 5 2 1 10 . x y z Câu 3.
Trong không gian Oxyz , cho đường thẳng 2 1 5 : và 2 điểm A 2 ;1; 1 , 1 3 2 B 3 ; 1
;2 . Điểm M ; a ;
b c (với c 0 ) thuộc đường thẳng sao cho MA B có diện tích
bằng 3 5 . Khi đó, tổng a + b + c bằng bao nhiêu ? Lời giải Trả lời: -30
M , suy ra tọa độ M 2
t;13t; 5 2t
Khi đó: AM t;3t; 6
2t và AB 1 ; 2 ; 1
AM , AB t
12;t 6;t Do S t 2 t 2 2 3 5 12 6 t 180 MAB t 0 M ( 2 ;1; 5 ) <=> 2
t 12t 0 t 1 2 M ( 1 4; 3 5;19)
Do c > 0 nên nhận M 1 4; 3 5;19
Khi đó: a b c 30 Câu 4.
Trong lễ kỷ niệm 30 năm thành lập trường THPT Chu Văn An – Biên Hòa (1994-2024), nhà
trường có cho dựng 1 cổng chào hình parabol với điểm cao nhất là 6m và chiều rộng giữa hai
chân cổng chào là 8m . Hỏi diện tích của cổng chào là bao nhiêu mét vuông ? Lời giải Trả lời: 32
Đặt hệ quy chiếu Oxy , vào 1 điểm chân cổng chào.
Khi đó, ta cần xác định hàm số 2
y ax bx c , biết parabol có đỉnh I 4;6 và đi qua gốc tọa độ O0;0 .
Thay tọa độ điểm O vào hàm số, suy ra: c 0 3 1
6a 4b 6 a
Ta có hệ phương trình: 8 8
a b 0 b 3 Suy ra hàm số 3 2 y x 3x 8
Diện tích của cổng chào: 8 3 2 S
x 3x dx 32 2 m 8 0 Câu 5.
Trong lớp học, màn hình tivi hình chữ nhật có chiều cao 1m được đặt ở độ cao 1, 2m so với tầm
mắt của học sinh (tính từ đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí ngồi
sao cho góc nhìn lớn nhất ( BOC là góc nhìn).
Nếu xét những học sinh ngồi nhìn thẳng màn hình thì học sinh ngồi bàn thứ mấy nhìn được rõ
nhất, biết bàn đầu tiên cách tivi 1, 2m và mỗi bàn kế tiếp nhau cách nhau 0,4m. Lời giải Trả lời: 2
Đặt OA x , ta có 2 OB x 1, 44 , 2 OC x 4,84 2 2 2
OB OC BC 2 x 2, 64 Ta có: cos BOC 2.O . B OC 2 2
x 1, 44. x 4,84 t 2, 64 Đặt t 2, 64 2
t x ,t 0 . Xét f (t)
t 1, 44. t 4,84 2
t 6, 28t 6, 9696 0,5t 1,32 Ta có: f ( t)
t 6, 28t 6,9696 3 2 Khi đó: f (
t) 0 t 2,64
Suy ra: cos BOC lớn nhất khi x 2, 64 1, 62 .
Do đó, học sinh ngồi bàn thứ 2 theo hướng nhìn thẳng màn hình sẽ có góc nhìn tốt nhất. Câu 6.
Gọi S là tập hợp tất cả các số tự nhiên gồm ba chữ số phân biệt được chọn từ các chữ số
1; 2;3; 4;5;6;7 . Chọn ngẫu nhiên một số chẵn từ tập S . Khi đó xác suất tìm được có dạng a b
(phân số tối giản). Tính a b . Lời giải Trả lời: 10
Số lượng không gian mẫu: n 3 A 210 7
Gọi A là biến cố lấy được số chẵn từ tập S. Ta có: n A 3.6.5 90
Khi đó: P A n A 90 3 n 210 7
Vậy a + b = 3 + 7 = 10.