Đề thi thử tốt nghiệp THPT 2025 môn Toán bám sát đề minh họa - Đề 34
Cho hình chóp tứ giác . SABCD có đáy ABCD là hình thoi tâm O, SOvuông góc với mặt đáy. Biết cạnh hình thoi bằng 2024, góc BAD bằng 120, khoảng cách từ điểm C đến mặt phẳng SBD bằng bao nhiêu? Một chiếc máy quay phim có trọng lượng. Tài liệu giúp bạn tham khảo, ôn tập và dạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2025 340 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
ĐỀ ÔN THI TỐT NGHIỆP THPT 2025 ĐỀ 34 MÔN: TOÁN Thời gian: 90 phút
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án. Câu 1.
Nghiệm của phương trình 3x 81 là A. 4 . B. 27 . C. 3 . D. 9 . Câu 2.
Cấp số nhân u có u 2 và u 4
. Số hạng u của cấp số nhân là n 1 2 6 A. 64 . B.128. C. 128 . D. 64 . Câu 3.
Trong không gian Oxyz , cho điểm M 1;2;
1 và mặt phẳng P : x 2y z 0 . Mặt phẳng
Q qua M và song song với Pcó phương trình là
A. x 2 y z 4 0 .
B. x 2 y z 1 0 .
C. x 2 y z 6 0 .
D. x 2 y z 4 0 . Câu 4.
Cho hình lập phương ABC . D A B C D
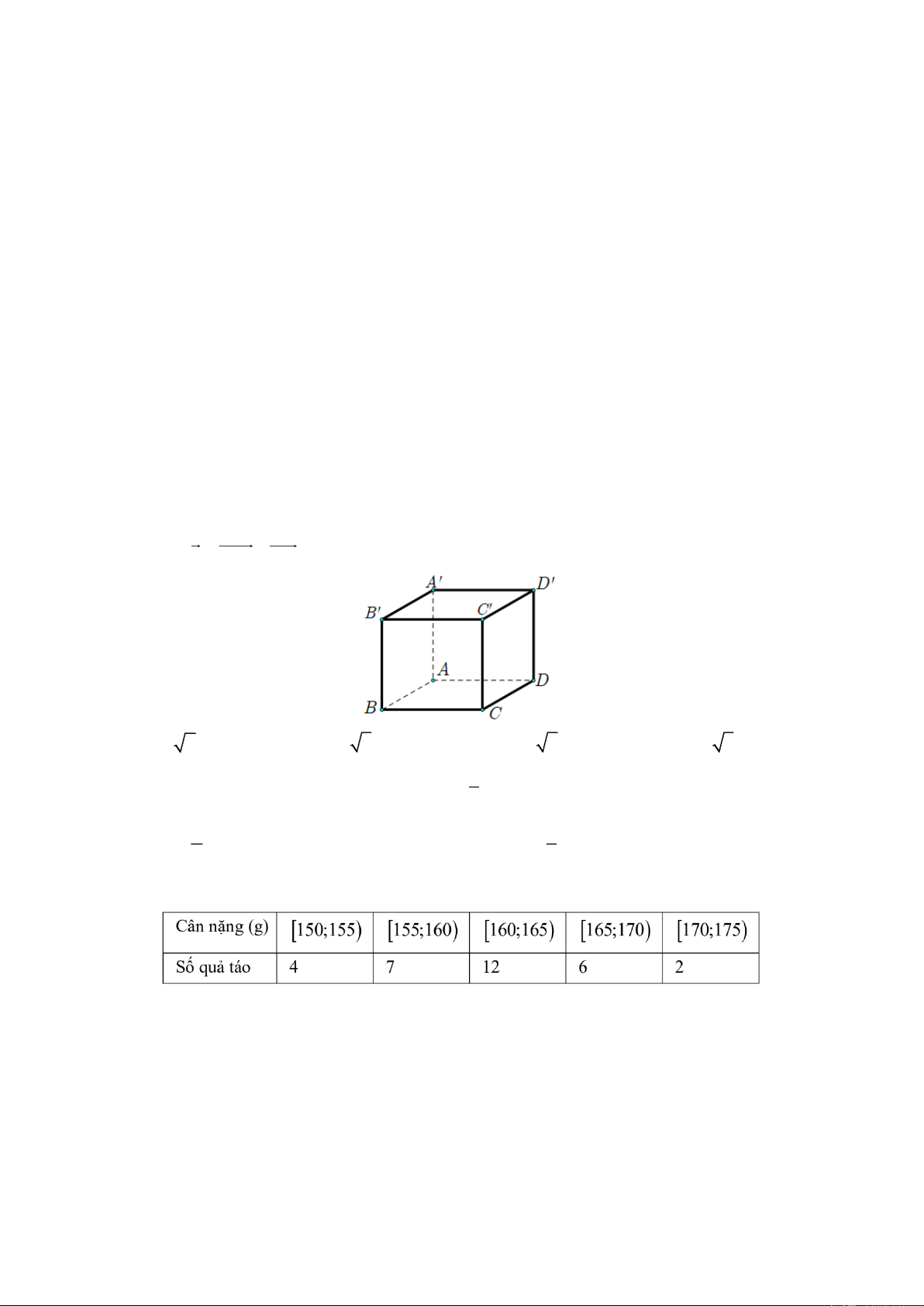
có cạnh 2 (tham khảo hình vẽ bên dưới). Độ dài của vectơ u A C A A bằng A. 2 2 . B. 3 . C. 2 6 . D. 2 3 . 1 Câu 5.
Tọa độ điểm cực tiểu của đồ thị hàm số 3 2 y
x 2x 3x 1 là 3 7 7 A. 4; . B. 3; 1 . C. 1; . D. 0; 1 . 3 3 Câu 6.
Kết quả khảo sát cân nặng của từng quả táo ở một lô hàng cho trong bảng sau:
Khoảng biến thiên R của mẫu số liệu ghép nhóm trên là A. R 5. B. R 24 . C. R 10 . D. R 25 . Câu 7.
Tập nghiệm của bất phương trình ln9 x 0 là A. 8; . B. 8;9 . C. ;8 . D. ;9 . Câu 8.
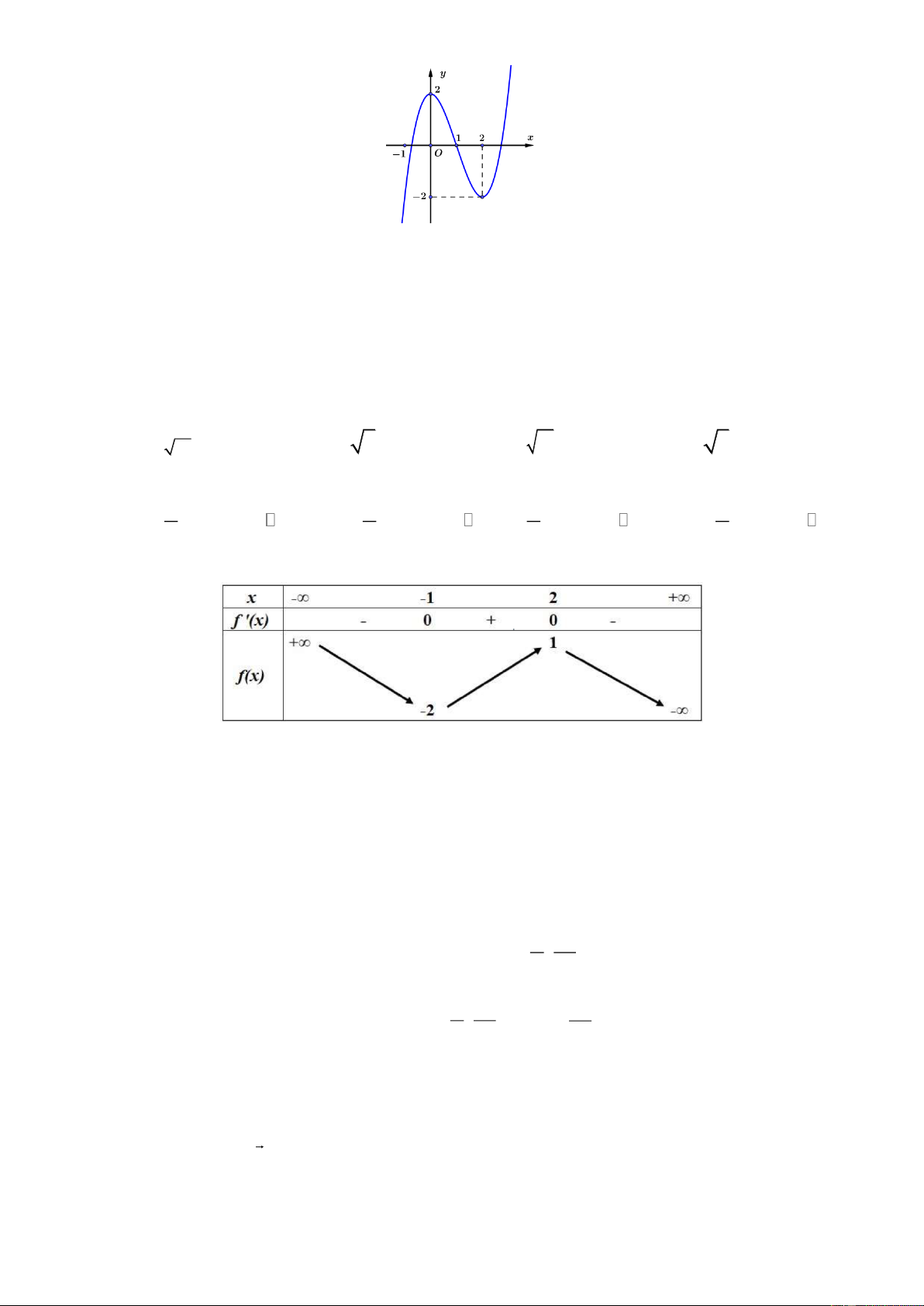
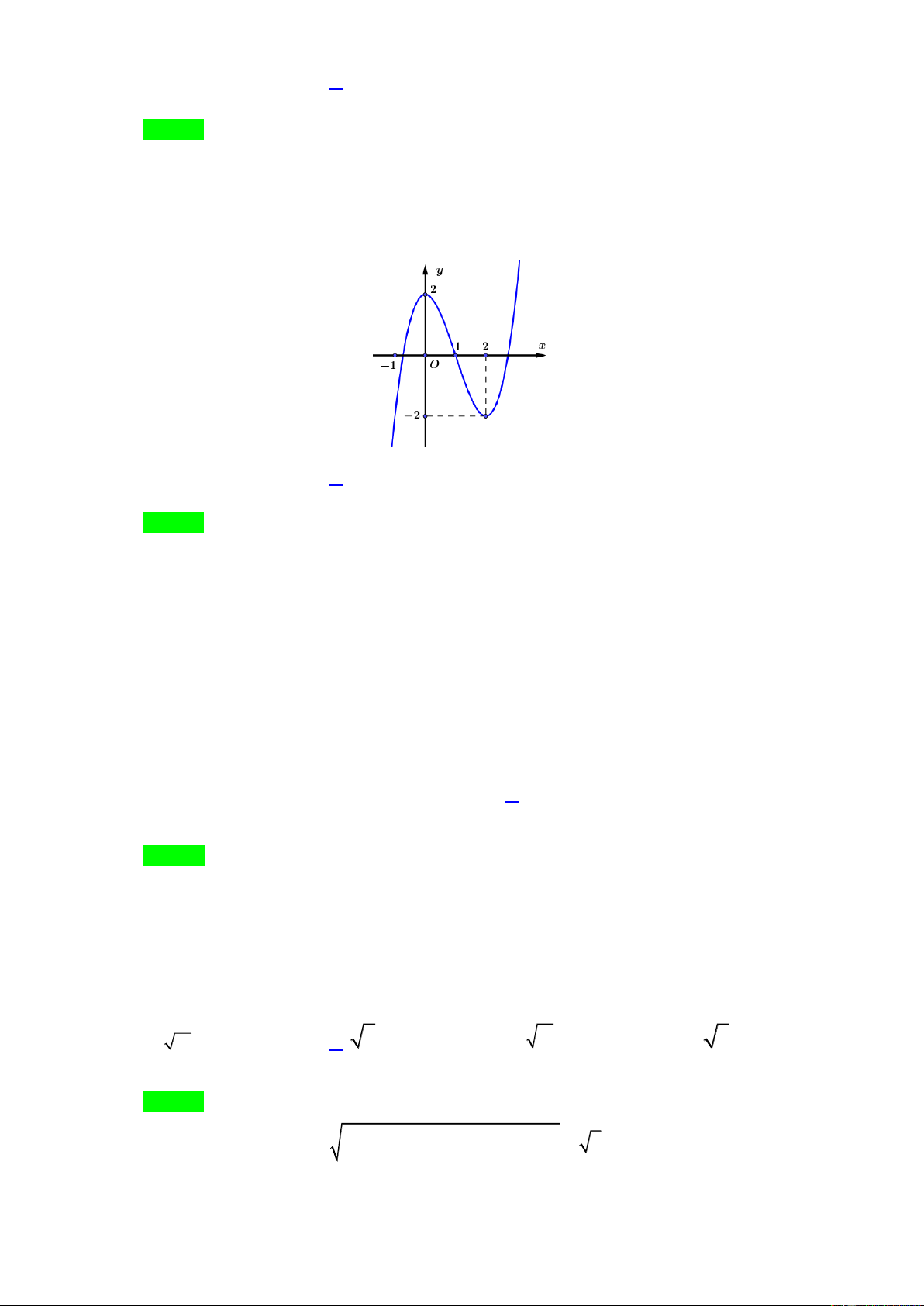
Đường cong ở hình sau là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3
y x 3x 2 . B. 3 2
y x 3x 2 . C. 3
y x 6x 2 . D. 3 2
y x 3x 2 . Câu 9.
Một người gửi tiết kiệm 10 triệu đồng vào một ngân hàng với lãi suất 7% /một năm. Biết rằng
tiền lãi được tính theo hình thức lãi kép. Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là
A.14, 026 triệu đồng.
B. 50, 7 triệu đồng.
C. 4, 026 triệu đồng.
D. 3,5 triệu đồng.
Câu 10. Trong không gian Oxyz , cho hai điểm A 1 ;2; 3 , B0;1;
1 . Độ dài đoạn AB bằng A. 12 . B. 6 . C. 10 . D. 8 .
Câu 11. Phương trình tan x 1
có tất cả các nghiệm là A.
k2 k . B.
k2 k . C. k k . D.
k k . 4 4 4 4
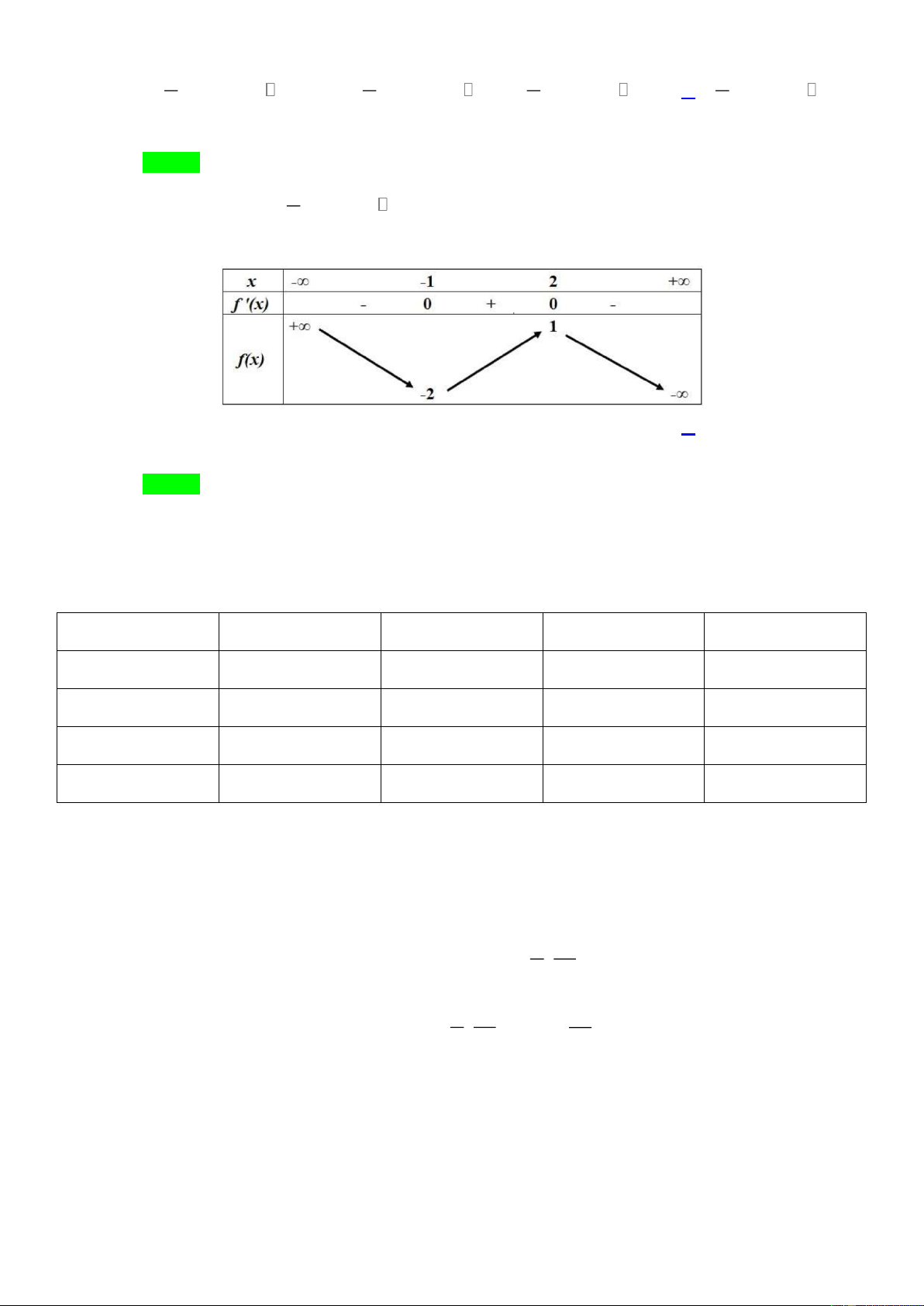
Câu 12. Cho hàm số bậc ba có bảng biến thiên như hình vẽ dưới đây. Giá trị cực tiểu của hàm số là A. 2 . B.1. C. 1. D. 2 .
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai. Câu 1.
Cho hàm số f x sin x x .
a) Đạo hàm của hàm số đã cho là f x cos x 1.
b) Nghiệm của phương trình f x 0 trên đoạn 3 ; là . 2 2 3
c) Giá trị nhỏ nhất của f x trên đoạn 3 ; là 1 . 2 2 2
d) f 0 0; f . Câu2.
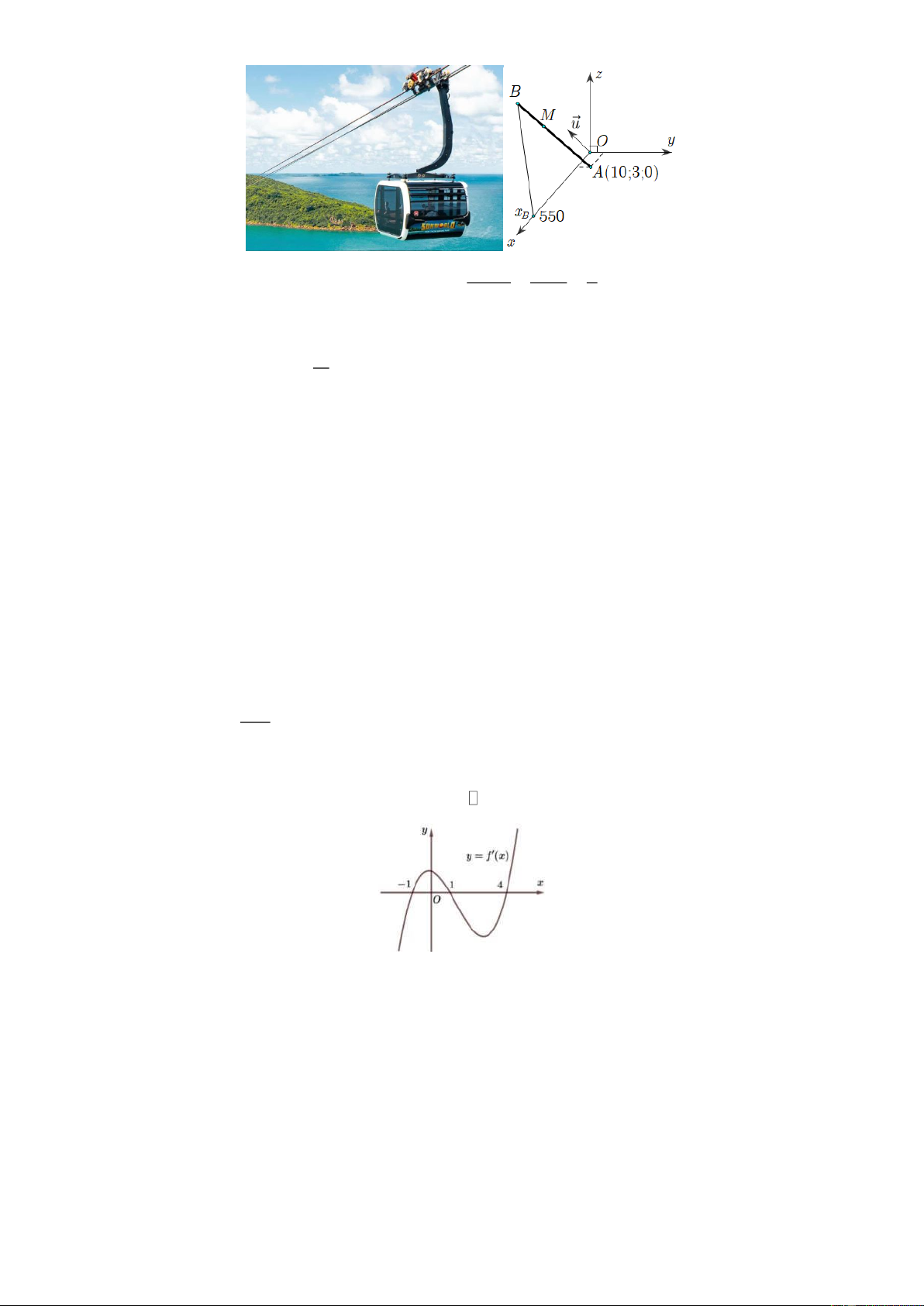
Một cabin cáp treo xuất phát từ điểm (10 A
;3; 0) và chuyển động đều theo đường cáp có véctơ
chỉ phương là u = 2; 2 ;
1 với tốc độ là 4,5 (m/s) (đơn vị trên mỗi trục tọa độ là mét) được mô
hình hóa như các hình vẽ sau: x 10 y 3 z
a) Phương trình chính tắc của đường cáp là 2 2 1
b) Giả sử sau t giây kể từ lúc xuất phát (t 0), cabin đến vị trí điểm M. Khi đó tọa độ của điểm 3t
M là 3t 10; 3 t 3; 2
c) Cabin dừng ở điểm B có hoành độ x = 550. Quãng đường AB B có độ dài bằng
810 (m) (làm tròn kết quả đến hàng đơn vị của mét).
d) Đường cáp AB tạovớimặt Oxy một góc 22 (làm tròn đến hàng đơn vị của độ). Câu 3.
Một hạt chuyển động trên một đường thẳng có gắn một trục toạ độ với gốc toạ độ là vị trí bắt
đầu chuyển động. Toạ độ của hạt trên trục tại thời điểm t (đơnvị: giây) kể từ khi xuất phát được
cho bởi công thức xt 2t 3lnt 1
(đơnvị:mét), t 0 . Hàm số vt xt (đơn vị:
mét/giây) biểu thị vận tốc chuyển động của hạt.
a) Quãng đường mà hạt đi được trong 3 giây đầu tiên là 1,84m (làm tròn kết quả đến hàng phần trăm).
b) Hạt đứng yên tại thời điểm t 0,5s . c) v t 3 2 t . 1
d) Vận tốc ban đầu của hạt là 1 m / s . Câu 4.
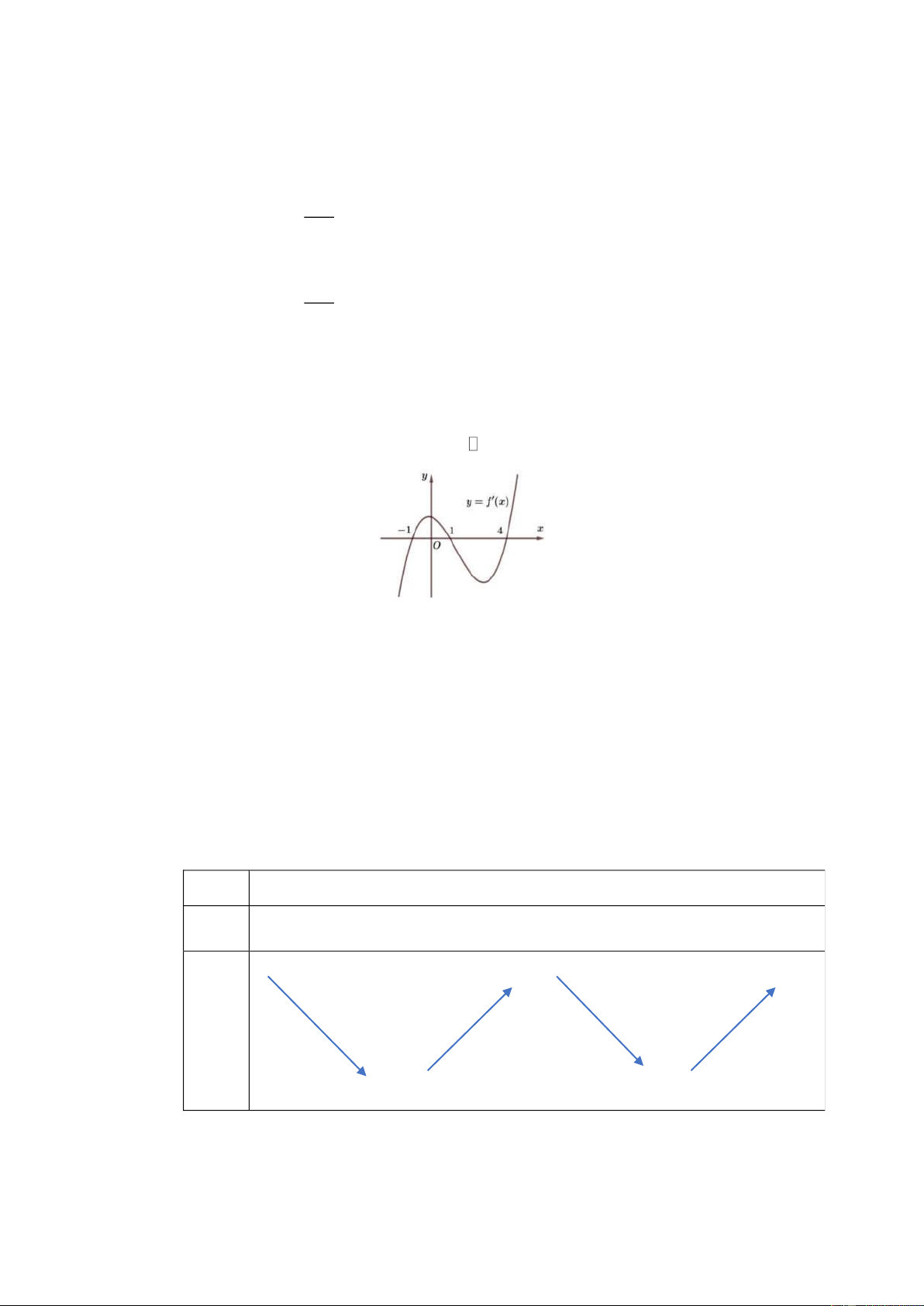
Cho hàm số y f x có đạo hàm liên tục trên
. Hàm số y f x có đồ thị như hình dưới đây.
a) Hàm số y f x đồng biến trên khoảng 1;. b) Trên đoạn 1
;4thì giá trị lớn nhất của hàm số y f xlà f 1 . c) f
1 f 2 f 4 .
d) Hàm số y f x có hai cực trị.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN Câu 1.
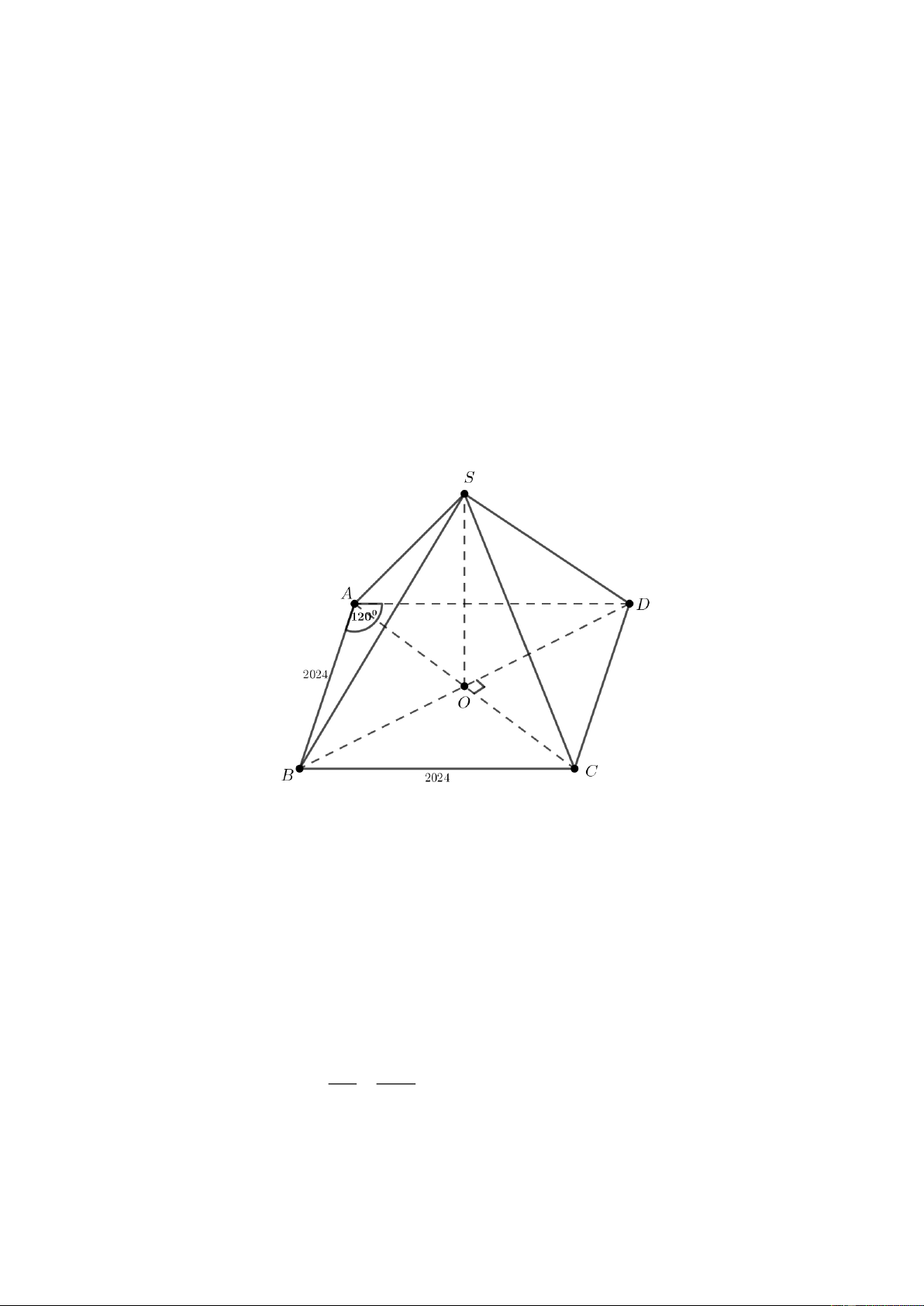
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thoi tâm O , SO vuông góc với mặt đáy.
Biết cạnh hình thoi bằng 2024, góc BAD bằng 120, khoảng cách từ điểm C đến mặt phẳng
SBD bằng bao nhiêu? Câu 2.
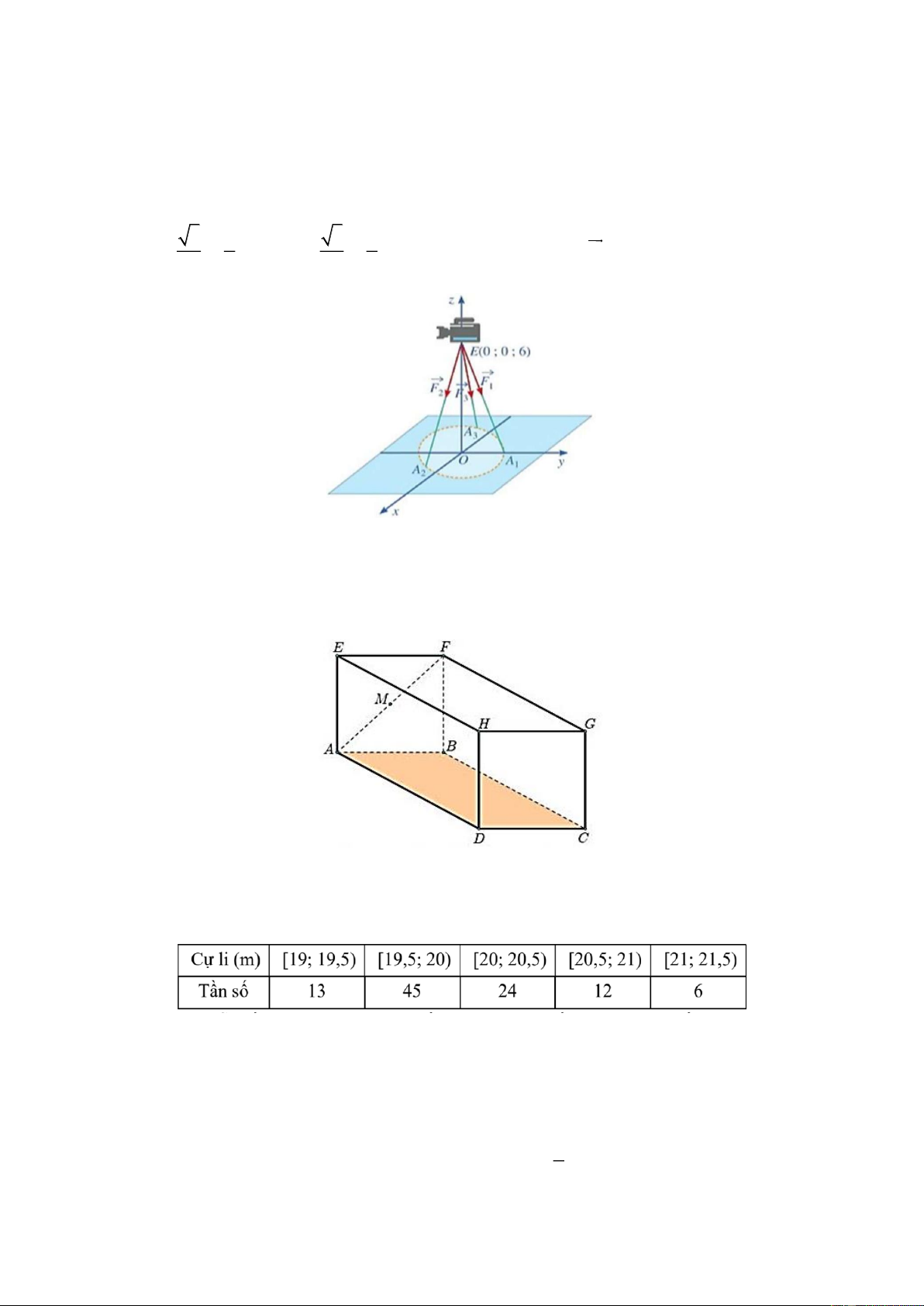
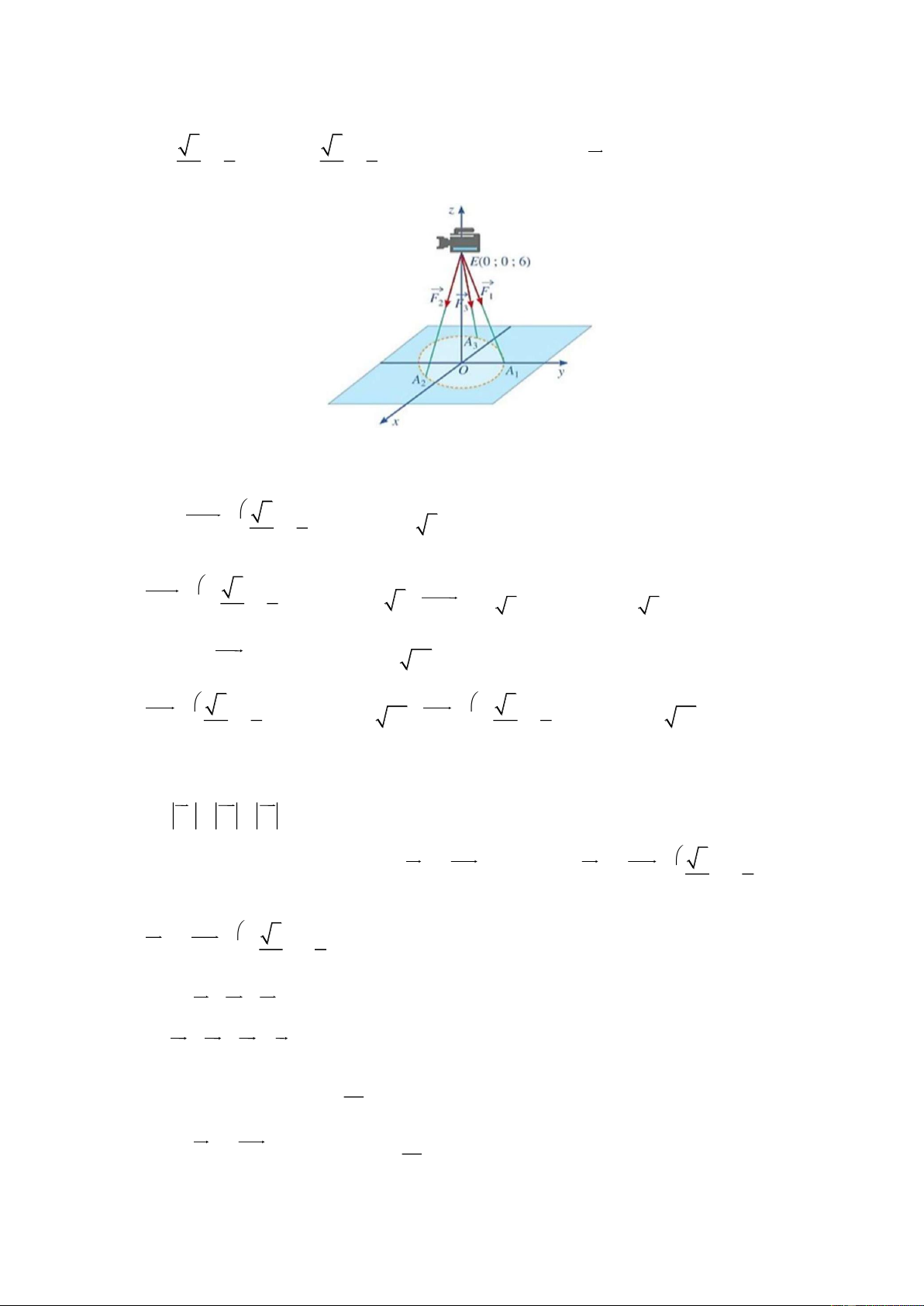
Một chiếc máy quay phim có trọng lượng 300N được đặt trên một giá đỡ ba chân với điểm
đặt E 0;0;6 và các điểm tiếp xúc với mặt đất của ba chân lần lượt là A 0;1;0 , 1 3 1 3 1 A ; ; 0 A
; ;0 (Hình bên dưới). Giả sử F a, ,
b c khi đó a 3b c bằng 1 2 , 2 2 3 2 2 Câu3.
Một bể cá đầy nước có dạng hình hộp chữ nhật ABC . D EFGH với
AB 6dm , AD 8dm và cạnh bên bằng 10dm .Một chú cá con bơi theo những đoạn
thẳng từ điểm G đến chạm mặt đáy của hồ, rồi từ điểm đó bơi đến vị trí điểm M là trung điểm
của AF được mô hình hóa như hình vẽ sau:
Để đường đi ngắn nhất thì chú cá bơi đến điểm dưới đáy hồ cách BA và BC những đoạn
bằng a và b . Khi đó tổng D 3a 6b bằng bao nhiêu? Câu 4.
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
Phương sai của mẫu số liệu ghép nhóm trên bằng bao nhiêu? (kết quả làm tròn đến hàng phần trăm)
Câu 5. Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:
Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ
và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích 1 ). 4
Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác,
mỗi tam giác có diện tích 1 ). 2 4
Cứ tiếp tục quá trình như vậy (ở bước thứ n , bỏ đi 1
3n tam giác, mỗi tam giác có diện tích 1 ). 4n
Tổng diện tích các tam giác đã bỏ đi bằng bao nhiêu? Câu 6.
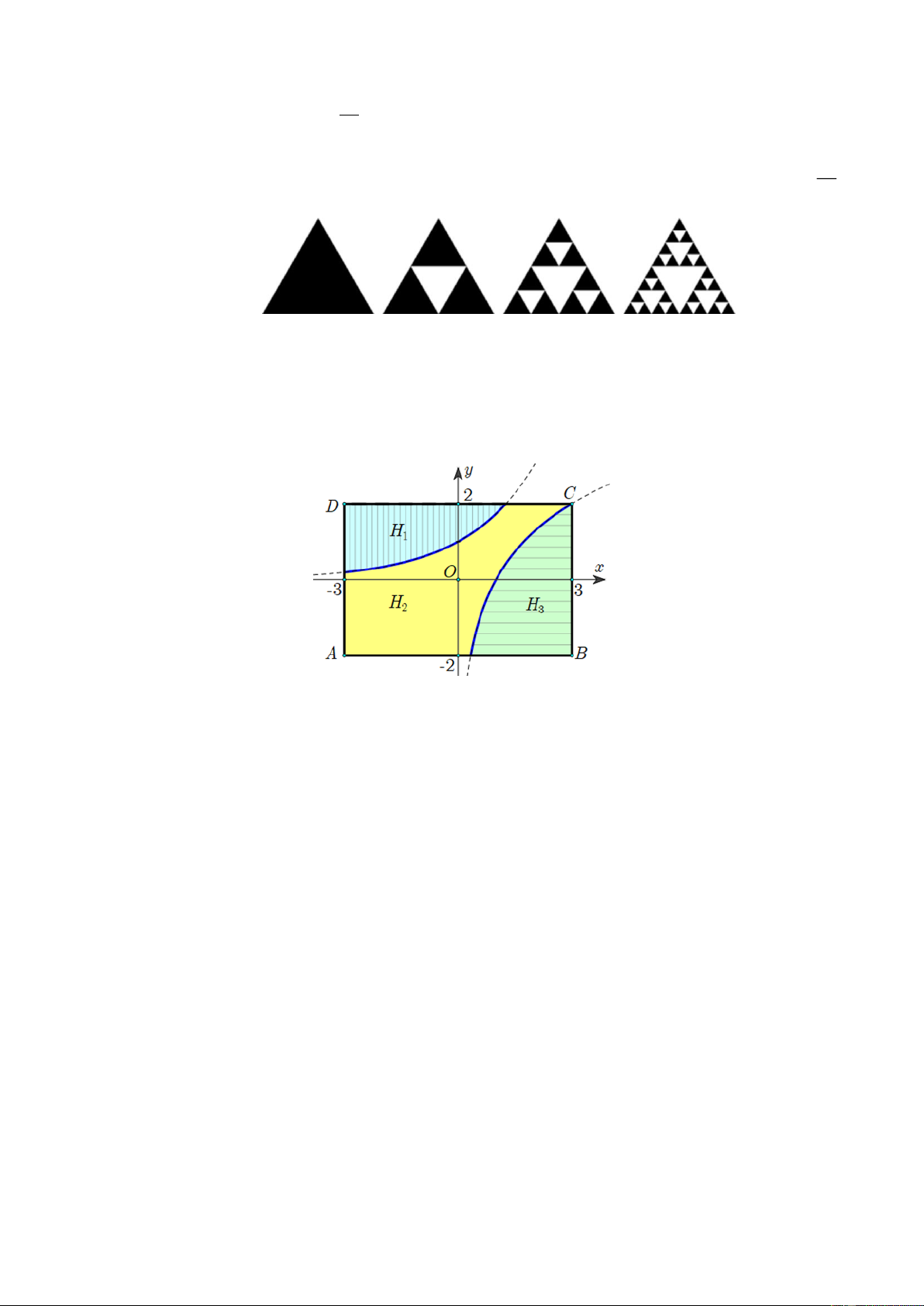
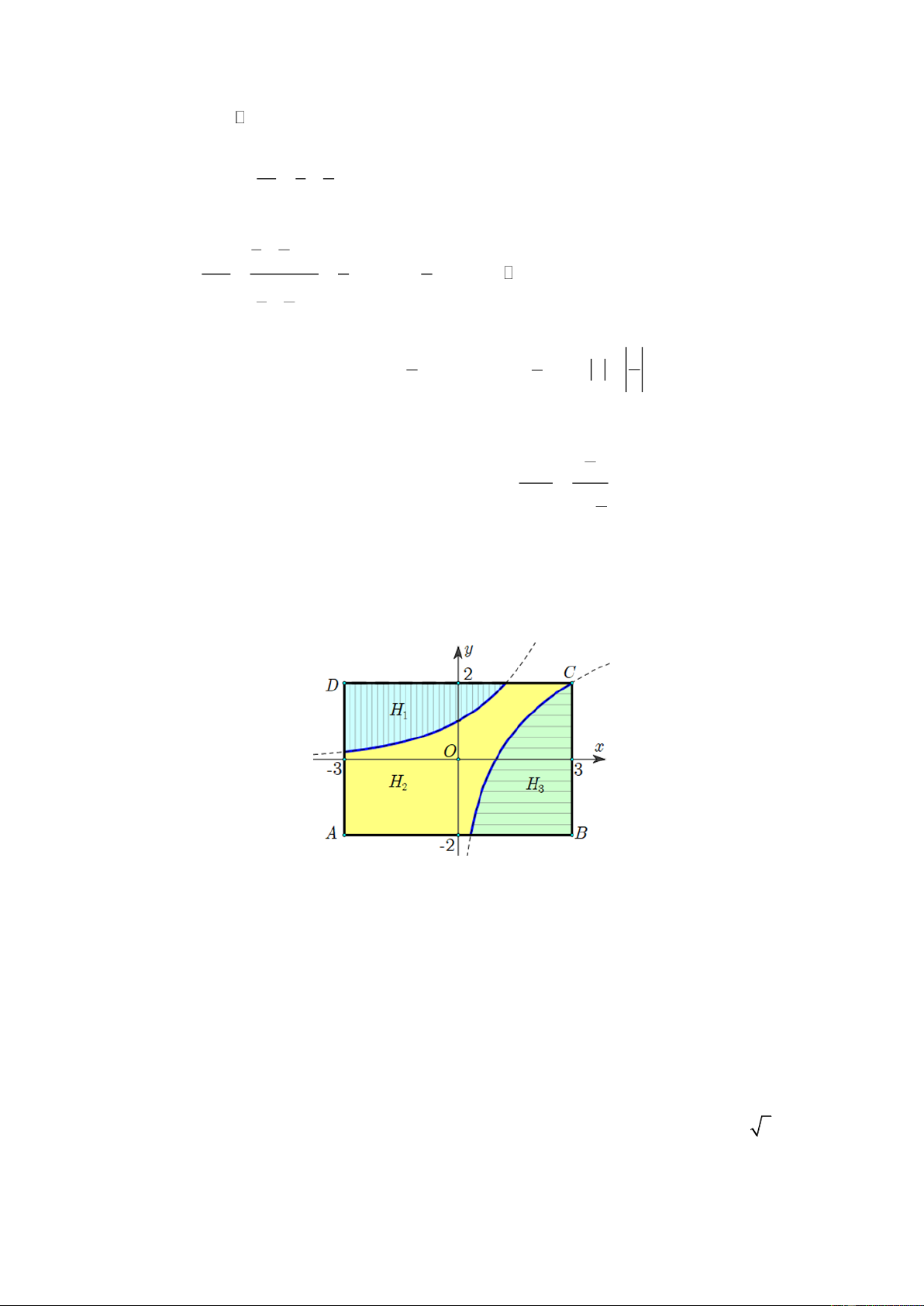
Một bức tường hình chữ nhật ABCD có kích thước 6m4m được bạn An trang trí bằng
cách vẽ hai đồ thị f x x
a , g x log x đối xứng nhau qua đường thẳng d : y x và chia b
thành ba phần (tham khảo hình vẽ bên).
Phần H được sơn màu xanh da trời, phần H được sơn màu vàng, phần H được sơn màu 1 2 3
xanh lá cây. Biết rằng mỗi hộp sơn các màu chỉ sơn được 2
3 m tường, đồng thời giá của hộp
sơn màu xanh da trời là 100.000đồng / hộp, hộp sơn vàng là 140.000đồng / hộp, hộp sơn xanh
lá cây là 130.000 đồng / hộp. Tính giá tiền bạn An mua để sơn bức tường này? (đơn vị là triệu
đồng và cửa hàng sơn chỉ bán số nguyên của hộp). ĐÁP ÁN
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A A D D B D B B C B D D
Hướng dẫn giải chi tiết Câu 1.
Nghiệm của phương trình 3x 81 là A. 4 . B. 27 . C. 3 . D. 9 . Lời giải Chọn A Ta có x x 4
3 81 3 3 x 4 . Câu 2.
Cấp số nhân u có u 2 và u 4
. Số hạng u của cấp số nhân là n 1 2 6 A. 64 . B.128. C. 128 . D. 64 . Lời giải Chọn A Ta có công bội u 4 2 q 2 . u 2 1
Do đó u u .q 2. 2 5 5 6 4 . 6 1 Câu3.
Trong không gian Oxyz , cho điểm M 1;2;
1 và mặt phẳng P : x 2y z 0 . Mặt
phẳng Q qua M và song song với P có phương trình là
A. x 2 y z 4 0 .
B. x 2 y z 1 0 .
C. x 2 y z 6 0 .
D. x 2 y z 4 0 . Lờigiải ChọnD
Ta có Q // P nên n Q nP 1;2; 1 .
Do đó phương trình mặt phẳng Q qua M và có vectơ pháp tuyến n P 1;2 ;1 : 1 x
1 2 y 2 1 z
1 0 x 2y z 4 0 Câu4.
Cho hình lập phương ABC . D A B C D
có cạnh 2 (tham khảo hình vẽ bên dưới). Độ dài của vectơ u A C A A bằng A. 2 2 . B. 3 . C. 2 6 . D. 2 3 . Lờigiải ChọnD Ta có 2 2 2 2 2 2 u A C A A
AC AA AB AD 2 2 2 12 2 3 . 1 Câu 5.
Tọa độ điểm cực tiểu của đồ thị hàm số 3 2 y
x 2x 3x 1 là 3 7 7 A. 4; . B. 3; 1 . C. 1; . D. 0; 1 . 3 3 Lời giải Chọn B 1 Ta có 3 2 2 y
x 2x 3x 1 y x 4x 3 . 3 1 1 3 2
x 1 y .1 2.1 3.11 2 3 3
y 0 x 4x 3 0 . 1 3 2
x 3 y .3 2.3 3.3 1 1 3 Bảng biến thiên x ∞ 1 3 +∞ y' + 0 0 + 1 +∞ y 3 ∞ 1
Vậy điểm cực tiểu của đồ thị hàm số là 3; 1 . Câu 6.
Kết quả khảo sát cân nặng của một thùng táo ở một lô hàng cho trong bảng sau:
Khoảng biến thiên R của mẫu số liệu ghép nhóm trên là A. R 5. B. R 24 . C. R 10 . D. R 25 . Lời giải Chọn D
Khoảng biến thiên R 175150 25. Câu 7.
Tập nghiệm của bất phương trình ln9 x 0 là A. 8; . B. 8;9 . C. ;8 . D. ;9 . Lời giải Chọn B
Điều kiện: 9 x 0 x 9 . x 0 ln 9
0 9 x e 9 x 1 x 8.
Kết hợp điều kiện x 9 ta được tập nghiệm của bất phương trình ln9 x 0 là 8;9. Câu 8.
Đường cong ở hình sau là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3
y x 3x 2 . B. 3 2
y x 3x 2 . C. 3
y x 6x 2 . D. 3 2
y x 3x 2 . Lời giải Chọn B
Từ đồ thị hàm số, dựa vào nhánh ngoài cùng bên phải ta suy ra a 0 nên loại phương án D .
Ta thấy đồ thị hàm số đi qua điểm A1;0 và điểm B2; 2
nên ta thế vào từng phương án.
Xét phương án A . Thế x 2 vào 3
y x 3x 2 ta được 3
y 2 3.2 2 4 2 nên sai.
Xét phương án B . Thế x 2 vào 3 2
y x 3x 2 ta được 3 2
y 2 3.2 2 2 . Thế x 1 vào 3 2
y x 3x 2 ta được 3 2
1 3.1 2 0 nên đúng.
Xét phương án C . Thế x 1 vào 3
y x 6x 2 ta được 3 1 6.1 2 3 0 nên sai. Câu9.
Một người gửi tiết kiệm 10 triệu đồng vào một ngân hàng với lãi suất 7% /một năm. Biết rằng
nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được cập nhật vào vốn
ban đầu. Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là
A.14, 026 triệu đồng.
B. 50, 7 triệu đồng.
C. 4, 026 triệu đồng.
D. 3,5 triệu đồng. Lời giải Chọn C
Ta có số tiền vốn lẫn lãi sau 5 năm của một người đã gửi vào ngân hàng là:
T T 1 r 5 5 10 1 0, 07 14,026 triệu đồng. 5 0
Vậy Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là 14,026 10 4,026 triệu đồng.
Câu 10. Trong không gian Oxyz , cho hai điểm A 1 ;2; 3 , B0;1;
1 . Độ dài đoạn AB bằng A. 12 . B. 6 . C. 10 . D. 8 . Lời giải Chọn B 2 Độ dài đoạn thẳng 2 2
AB là 0
1 1 2 13 6 . Câu11.
Phương trình tan x 1
có tất cả các nghiệm là A.
k2 k . B.
k2 k . C. k k . D.
k k . 4 4 4 4 Lờigiải ChọnD tan x 1
x k k . 4
Câu12. Cho hàm số bậc ba có bảng biến thiên như hình vẽ dưới đây. Giá trị cực tiểu của hàm số là A. 2 . B.1. C. 1. D. 2 . Lờigiải ChọnD
Giá trị cực tiểu của hàm số là y 2 . CT
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI Câu 1 Câu 2 Câu 3 Câu 4 A Đ Đ Đ S B S Đ Đ Đ C Đ Đ Đ Đ D Đ S S S
Hướng dẫn giải chi tiết Câu 1.
Cho hàm số f x sin x x .
a) Đạo hàm của hàm số đã cho là f x cos x 1.
b) Nghiệm của phương trình f x 0 trên đoạn 3 ; là . 2 2 3
c) Giá trị nhỏ nhất của f x trên đoạn 3 ; là 1 . 2 2 2
d) f 0 0; f . Lời giải a) Đúng.
Ta có : f x sin x x f x cos x 1 b) Sai.
Ta có: f x cos x 1 khi đó f x 0 cos x 1 0 cos x 1 x k2 k . 3 3 1 3 Do x ; nên k2 , k
k , k . Suy ra phương trinh f x 0 2 2 2 2 4 4
không có nghiệm trên đoạn 3 ; 2 2 c) Đúng. Do f x 3
cos x 1 0, x ;
nên hàm số đã cho nghịch biến trên đoạn 3 ; 2 2 2 2
Khi đó hàm số đạt GTNN là 3 1 tại 3 x 2 2 d) Đúng.
Do f x sin x x nên ta có:
f 0 sin 0 0 0 và f sin Câu2.
Một cabin cáp treo xuất phát từ điểm (10 A
;3; 0) và chuyển động đều theo đường cáp có véctơ
chỉ phương là u = 2; 2 ;
1 với tốc độ là 4,5 (m/s) (đơn vị trên mỗi trục tọa độ là mét) được mô
hình hóa như các hình vẽ sau: x 10 y 3 z
a) Phương trình chính tắc của đường cáp là 2 2 1
b) Giả sử sau t giây kể từ lúc xuất phát (t 0), cabin đến vị trí điểm M. Khi đó tọa độ của điểm 3t
M là 3t 10; 3 t 3; 2
c) Cabin dừng ở điểm B có hoành độ x = 550. Quãng đường AB B có độ dài bằng
810 (m) (làm tròn kết quả đến hàng đơn vị của mét).
d) Đường cáp AB tạovớimặt Oxy một góc 22 (làm tròn đến hàng đơn vị của độ). Lời giải a) Đúng.
Đường cáp đi qua điểm A10;3;0 và có véctơ chỉ phương là u = 2; 2 ; 1 nên có phương trình chính tắ x 10 y 3 z c là 2 2 1 b) Đúng. Gọi M ; x ;
y z ta có AM x 10; y 3; z , u = 3 .
Giả sử sau t giây kể từ lúc xuất phát (t 0), cabin đến vị trí điểm M.
x 10 3t 4, 5t Khi đó AM
.u AM = 1, 5t.u y 3 3t u 3 z t 2 3t
Suy ra tọa độ của điểm M là 3t 10; 3 t 3; 2 c) Đúng.
Cabin dừng ở điểm B có hoành độ x = 550. B x 10 y 3 z
Từ phương trình chính tắc là
và x = 550 suy ra y = 5
37và z = 270 . 2 2 1 B B B AB x
y 2 z 2 2 2 2 2 ( 10) 3 (540 10) 537 3 270 810 B B B
Quãng đường AB có độ dài bằng 810 (m) . d) Sai.
Đường cáp AB có véctơ chỉ phương là u = 2; 2 ; 1
Mặt phẳng Oxycó phương trình z 0, có vectơ pháp tuyến n = 0;0 ;1 AB O xy . u n 2.0 2.0 1.1 1 sin , = . u . n 5.1 5
Đường cáp AB tạo với mặt Oxymột góc 27(làm tròn đến hàng đơn vị của độ). Câu 3.
Một hạt chuyển động trên một đường thẳng có gắn một trục toạ độ với gốc toạ độ là vị trí bắt
đầu chuyển động. Toạ độ của hạt trên trục tại thời điểm t (đơnvị: giây) kể từ khi xuất phát được
cho bởi công thức xt 2t 3lnt 1
(đơnvị:mét), t 0 . Hàm số vt xt (đơn vị:
mét/giây) biểu thị vận tốc chuyển động của hạt.
a) Quãng đường mà vật đi được trong 3 giây đầu tiên là 1,84m (làm tròn kết quả đến hàng phần trăm).
b) Hạt đứng yên tại thời điểm t 0,5s . c) v t 3 2 t . 1
d) Vận tốc ban đầu của hạt là 1 m / s . Lời giải a) Đúng. Vì: x
3 x 0 6 3ln 4 6 6ln 2 1,84m. Nên quãng đường mà vật đi được trong 3 giây
đầu tiên là 1,84m . b) Đúng.
Vì: v t xt 3 2
và v 0,5 0 nên hạt đứng yên tại thời điểm t 0,5s t 1 c) Đúng.
Vì: v t xt 3 2 t 1 d) Sai. Vì: v 0 1
m / s nên vận tốc ban đầu của hạt là 1m / s (dấu âm biểu thị hạt di chuyển ngược chiều dương) Câu 4.
Cho hàm số y f x có đạo hàm liên tục trên
. Hàm số y f x có đồ thị như hình dưới đây.
a) Hàm số y f x đồng biến trên khoảng 1;. b) Trên đoạn 1
;4thì giá trị lớn nhất của hàm số y f xlà f 1 . c) f
1 f 2 f 4 .
d) Hàm số y f x có hai cực trị. Lời giải a) Sai.
Từ đồ thị hàm số y f x ta có bảng biến thiên của hàm số y f x như sau: x 1 1 4
f x 0 0 0 f 1 f x f 1 f 4
Dựa vào bảng biến thiên hàm số y f x đồng biến trên các khoảng 1 ; 1 và 4; . b) Đúng.
Dựa vào bảng biến thiên, trên đoạn 1
;4thì giá trị lớn nhất của hàm số y f x là f 1 . c) Đúng.
Dựa vào bảng biến thiên, hàm số y f x nghịch biến trên đoạn1; 4 , do vậy f
1 f 2 f 4 . d) Sai.
Dựa vào bảng biến thiên, hàm số y f x có ba điểm cực trị.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN Câu 1.
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thoi tâm O , SO vuông góc với mặt đáy.
Biết cạnh hình thoi bằng 2024, góc BAD bằng 120, khoảng cách từ điểm C đến mặt phẳng
SBD bằng bao nhiêu? Lời giải Đáp số:1012.
Xét tam giác ABC có:
AB BC (tứ giác ABCD là hình thoi)
ABC 180 DAB 180 120 60
tam giác ABC đều
AB BC AC 2024.
Ta có: CO BD (tứ giác ABCD là hình thoi)
CO SO (do SO ABCD )
CO SBD
d C SBD AC 2024 , CO 1012 . 2 2 Câu 2.
Một chiếc máy quay phim có trọng lượng 300N được đặt trên một giá đỡ ba chân với điểm
đặt E 0;0;6 và các điểm tiếp xúc với mặt đất của ba chân lần lượt là A 0;1;0 , 1 3 1 3 1 A ; ; 0 A
; ;0 (Hình bên dưới). Giả sử F a, ,
b c khi đó a 3b c bằng 1 2 , 2 2 3 2 2 Lời giải Đáp số: 150. 3 3 Ta có A A
; ;0 A A 3 1 2 1 2 2 2 3 3 A A
; ;0 A A 3 1 3 1 3 ; A A 3; 0; 0 A A 3 2 3 2 2 2 3
Mặt khác EA 0;1; 6 EA 37 1 1 3 1 3 1 EA
; ; 6 EA 37 EA ; ; 6 EA 37 2 2 ; 2 2 3 3 2 2
Suy ra tam giác A A A là tam giác đều và hình chóp .
E A A A là hình chóp đều 1 2 3 1 2 3 nên F 1 F F . 2 3 3 k
Vì thế tồn tại hằng số k 0 sao cho F k EA 0;k; 6
k ; F k EA k; ; 6 k 1 1 2 2 2 2 3 k
F k EA k; ; 6 k 3 3 2 2
Suy ra F F F 0;0; 1 8k . 1 2 3
Mà F F F P 0;0; 3
00 là vectơ trọng lượng máy quay. 1 2 3 Do đó 50 18 k 30 0 k 3 50
Suy ra F k EA 0; k; 6 k 0; ; 10 0 1 1 3 Do đó 50
a 3b c 0 3. 10 0 150. 3 Câu3.
Một bể cá đầy nước có dạng hình hộp chữ nhật ABC . D EFGH với
AB 6dm , AD 8dm và cạnh bên bằng 10dm .Một chú cá con bơi theo những đoạn
thẳng từ điểm G đến chạm mặt đáy của hồ, rồi từ điểm đó bơi đến vị trí điểm M là trung điểm
của AF được mô hình hóa như hình vẽ sau:
Để đường đi ngắn nhất thì chú cá bơi đến điểm dưới đáy hồ cách BA và BC những đoạn
bằng a và b . Khi đó tổng D 3a 6b bằng bao nhiêu? Lời giải Đáp số: 20 .
Chọn hệ trục tọa độ như hình vẽ
Tacó: G 8;6;10 , M 0;3;5 .
Gọi M là điểm đối xứng với điểm M qua mặt phẳng Oxysuy ra M0;3; 5 .
Phương trình đường thẳng M G qua M0;3; 5 nhận M G
8;3;15làm vectơ chỉ phương x 8t
là: y 3 3t t . z 5 15t Gọi 8
P là giao điểm của đường thẳng M G
và mặt phẳng Oxy suy ra P ;4;0 . 3 8 a
Điểm P cách BA một khoảng bằng 8 và cách BC một khoảng bằng 2. Do đó: 3 . 3 b 2 Vậy 8
D 3a 6b 3. 6.2 20 . 3 Câu 4.
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
Phương sai của mẫu số liệu ghép nhóm trên bằng bao nhiêu? (kết quả làm tròn đến hàng phần trăm) Lời giải Đáp số: 0, 28 .
Ta có bảng các giá trị đại diện
Ta có giá trị trung bình của mẫu số liệu là
13.19, 25 45.19, 75 24.20, 25 12.20, 75 6.21, 25 x 20,015 13 45 24 12 6
Phương sai của mẫu số liệu là:
13.19, 25 20, 0152 45.19, 75 20, 0152 24.20, 25 20, 0152 12.20, 75 20, 0152 6.21, 25 20, 0152 2 s 13 45 24 12 6 0,28
Câu 5. Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:
Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ
và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích 1 ). 4
Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác,
mỗi tam giác có diện tích 1 ). 2 4
Cứ tiếp tục quá trình như vậy (ở bước thứ n , bỏ đi 1
3n tam giác, mỗi tam giác có diện tích 1 ). 4n
Tổng diện tích các tam giác đã bỏ đi bằng bao nhiêu? Lời giải Đáp số: 1. Gọi u ( * n
) là diện tích tam giác bỏ đi ở bước thứ n . n n n 1 1 3 Ta có 1 u 3 . . . n 4n 3 4 n 1 1 3 . Do đó: u n 3 4 3 3 1
u u , * n n n 1 n u n 1 3 4 4 . 3 4 1
Suy ra u là cấp số nhân có u , công bội 3 q thỏa 3 q
1. Vậy u là cấp số n n 1 4 4 4 nhân lùi vô hạn. 1
Do đó tổng diện tích các tam giác đã bỏ đi là: u1 4 S 1. 1 q 3 1 4 Câu 6.
Một bức tường hình chữ nhật ABCD có kích thước 6m4m được bạn An trang trí bằng
cách vẽ hai đồ thị f x x
a , g x log x đối xứng nhau qua đường thẳng d : y x và chia b
thành ba phần (tham khảo hình vẽ bên).
Phần H được sơn màu xanh da trời, phần H được sơn màu vàng, phần H được sơn màu 1 2 3
xanh lá cây. Biết rằng mỗi hộp sơn các màu chỉ sơn được 2
3 m tường, đồng thời giá của hộp
sơn màu xanh da trời là 100.000đồng / hộp, hộp sơn vàng là 140.000đồng / hộp, hộp sơn xanh
lá cây là 130.000 đồng / hộp. Tính giá tiền bạn Hà mua để sơn bức tường này? (đơn vị là triệu
đồng và cửa hàng sơn chỉ bán số nguyên của hộp). Lời giải Đáp số:1,15 .
Hai đồ thị f x x
a , g x log x đối xứng nhau qua đường thẳng d : y x . b khi a b
Điểm 3;2 thuộc đồ thị hàm số g x log x nên 2
log 3 2 b 3 a b 3 . b b Tac ó: S
S S S 6.4 24 . 1 H H2 H3 ABCD log 2 3 x x
Xét 3 2 x log 2 S 2 3 dx 5, 23
nên cần mua 2 hộp sơn màu 3 H1 3 xanh da trời. 3 1 Xét log x 2
x S log x 2 dx 7,14
nên cần mua 3 hộp sơn màu xanh lá 3 3 3 3 H 1 3 cây. S 24 S S Ta có: H H H 2 1 3
3,87 S 11,61 nên cần mua 4 hộp sơn màu vàng. H2 3 3
Số tiền mua sơn là: 2.0,1 3.0,13 4.0,14 1,15 (triệu đồng).