Đề thi thử tốt nghiệp THPT 2025 môn Toán bám sát đề minh họa - Đề 44

ĐỀ BÁM SÁT CẤU TRÚC
ĐỀ LUYỆN THI TỐT NGHIỆP THPT NĂM 2025 ĐỀ THAM KHẢO 2025 Môn: TOÁN ĐỀ 44
Thời gian làm bài: 90 phút, không kể thời gian phát đề
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. 1
Câu 1. Cho cấp số nhân u có u  ;u  9
 . Công bội q của cấp số nhân là n  1 4 3 1 A. . 3 1 B.  . 3 C. 3  . D. 3. 1
Câu 2. Nghiệm của phương trình log x  5  là: 16   2
A. x  3. B. x  1  . C. x  3  . D. x  27 .
Câu 3. Họ tất cả các nguyên hàm của hàm số f  x  2x  6 là A. 2
x  C . B. 2
x  6x  C . C. 2
2x  C . D. 2
2x  6x  C . 2x  3
Câu 4: Tiệm cận ngang của đồ thị hàm số y  x  là 1 A. y  1. B. y  2 . C. x  1. D. x  2 .
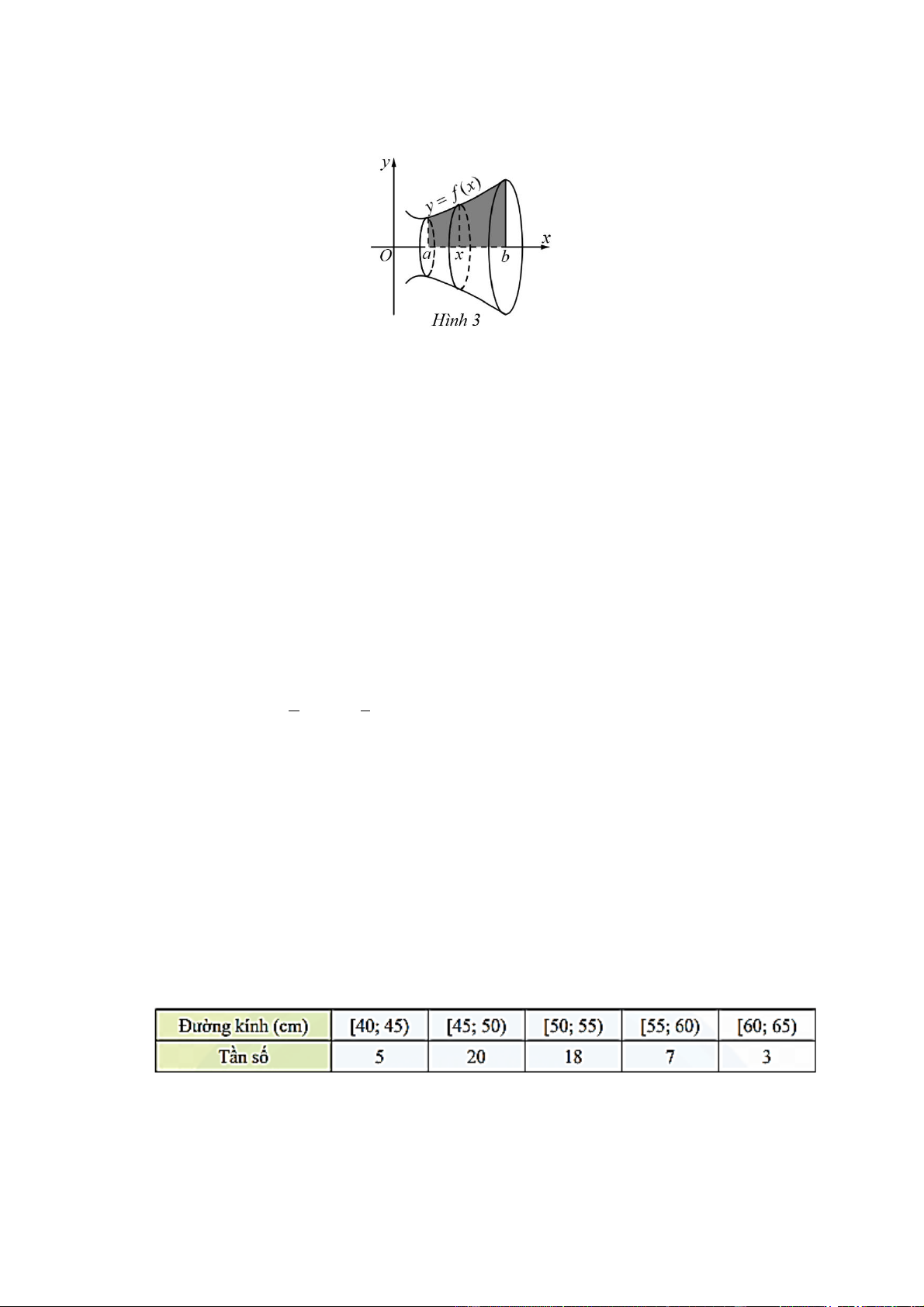
Câu 5. Cho hàm số y  f (x) liên tục, không âm trên đoạn [a; b] như Hình 3. Hình phẳng (H ) giới hạn
bởi đồ thị hàm số y  f (x), trục hoành và hai đường thẳng x  a, x  b quay quanh trục Ox tạo thành
một khối tròn xoay có thể tích bằng: a
A. V   f (x)d . x  b b
B. V  |f (x) | d . x  a b C. 2
V  [ f (x)] d . x  a b D. 2
V   [ f (x)] d . x  a 2 x 2 x  1  1
Câu 6. Bất phương trình    có tập nghiệm là  2  8 A. 3;. B.  ;    1 . C.  1  ;  3 . D.  1  ;3. Câu 7.
Một người công nhân của một nông trường thống kê lại đường kính thân gỗ của một số cây
keo lá tràm 7 năm tuổi được trồng ở một lâm trường ở bảng mẫu số liệu ghép nhóm sau
Khoảng biến thiên của mẫu số liệu ghép nhóm bằng A. 25 cm .
B. 5 cm .
C. 20 cm . D. 10 cm .
Câu 8. Trong không gian với hệ trục tọa độ Oxyz, vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng
(P) : 2x  y  z  3  0 ? A. n  (2; 1  ; 1 ). 1 B. n  (2; 1 ; 1 ). 2 C. n  (2; 1  ; 3). 3 D. n  ( 1  ; 1 ; 3). 4
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA vuông góc với đáy. Gọi M là
trung điểm AC . Khẳng định nào sau đây sai? A. BM ^ AC.
B. (SBM )^ (SAC).
C. (SAB)^ (SBC).
D. (SAB)^ (SAC).
Câu 10.Trong không gian Oxyz , cho mặt cầu (S ) có tâm I (2;3; 0) và bán kính bằng 2. Phương trình của (S ) là A. 2 2 2
(x  2)  ( y  3)  z  4 . B. 2 2 2
(x  2)  ( y  3)  z  2 . C. 2 2 2
(x  2)  ( y  3)  z  4 . D. 2 2 2
(x  2)  ( y  3)  z  2 .
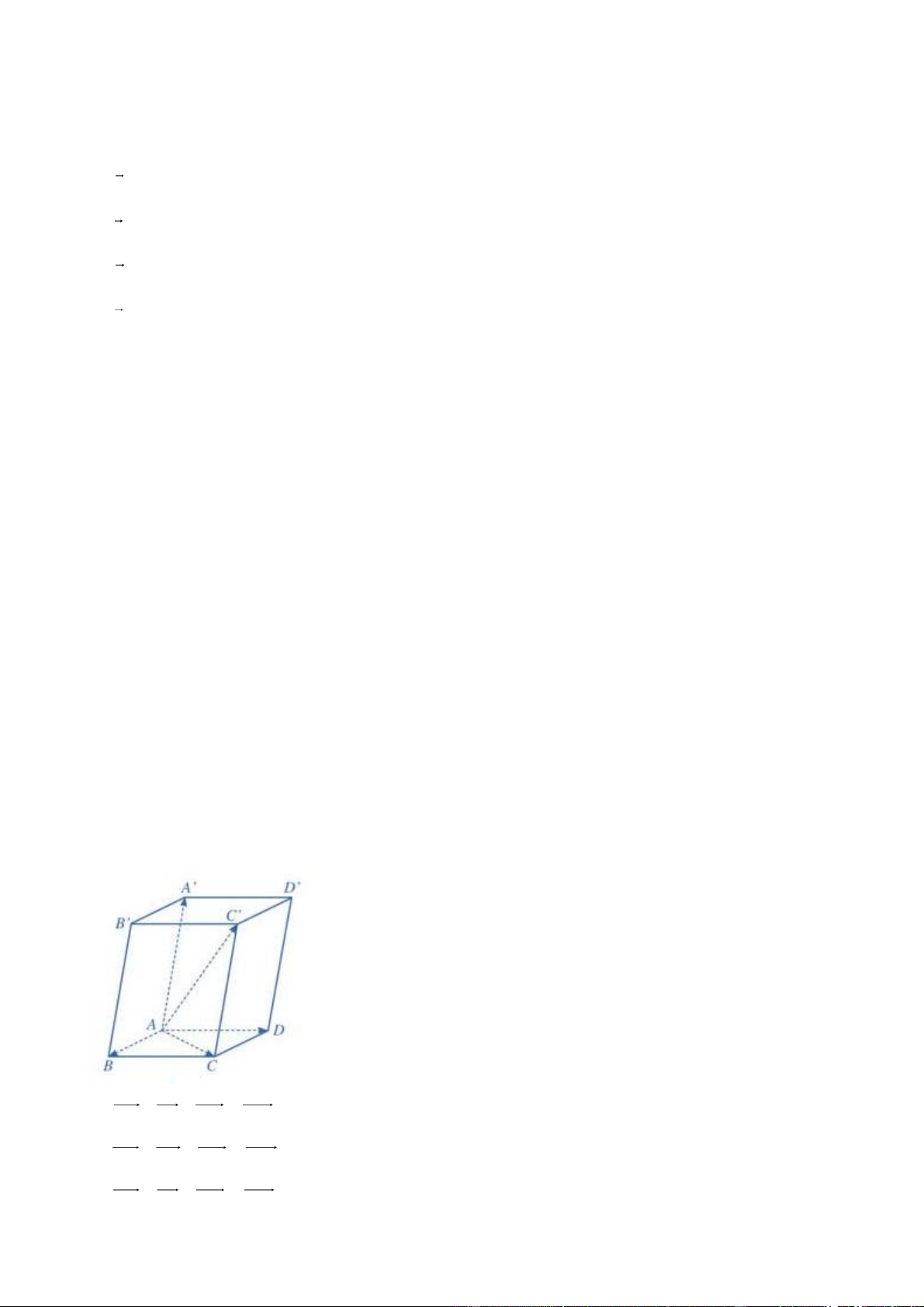
Câu 11. Cho hình hộp ABC .
D A B C D . Chọn đẳng thức đúng? 1 1 1 1
A. BC  BA  BB '  BC ' .
B. AD  AB  AA'  AC ' .
C. BD  BA  BB '  BD ' .
D. BA  BB '  BD  BD ' .
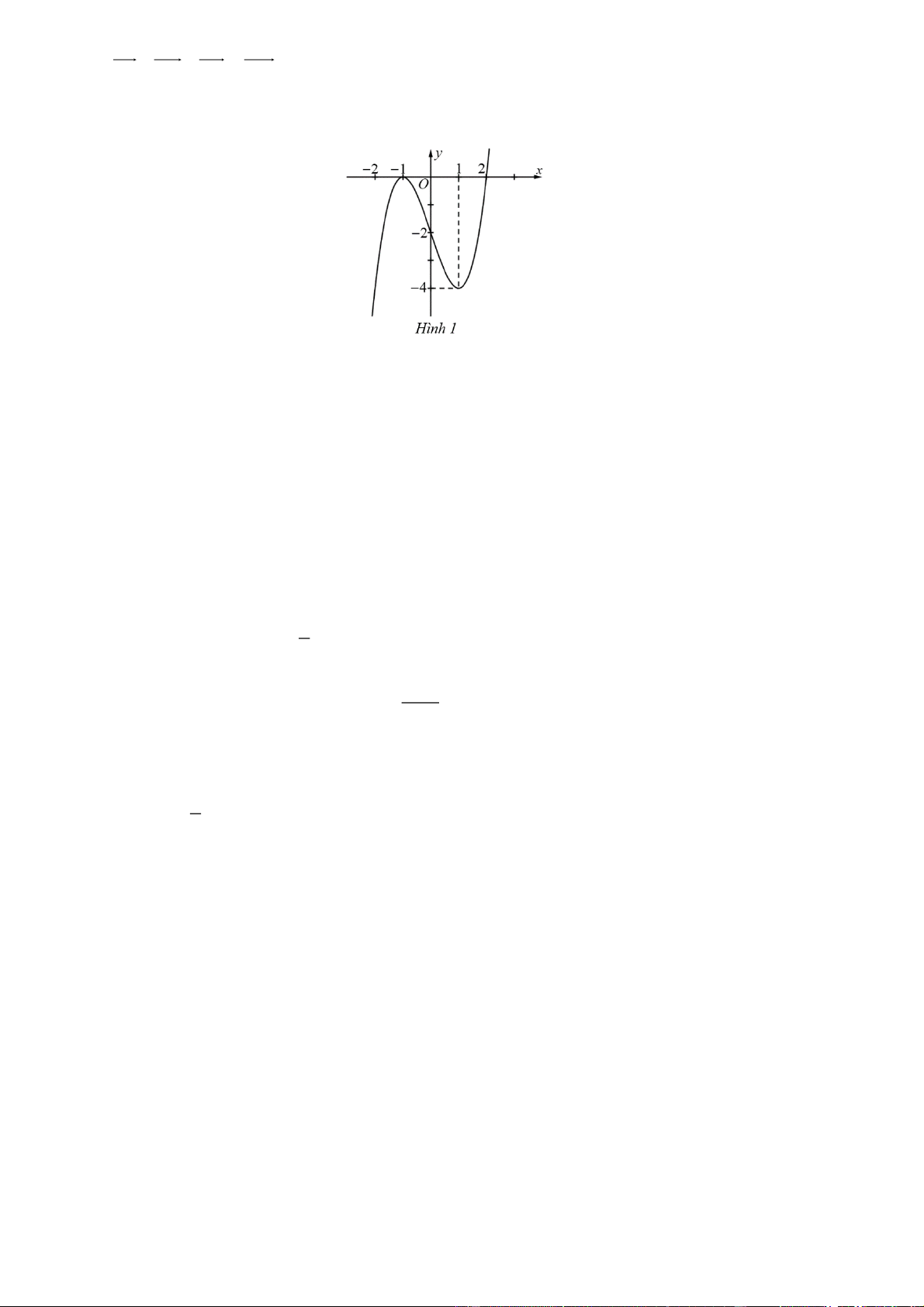
Câu 12. Cho hàm số y  f (x) có đồ thị như Hình 1.
Điểm cực tiểu của hàm số đã cho là: A. x  1  . B. x  1. C. x  2 . D. x  4  .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. 1
Câu 1. Cho hàm số f  x 2
 x  x  6ln x  2. 2
a) Đạo hàm của hàm số là f  x 6 '  x 1 . x  2 b) Trên đoạn  1  ; 
2 , phương trình f ' x  0 có hai nghiệm phân biệt. c) f   1 1  
và f 2  4 12ln 2. 2
d) Giá trị nhỏ nhất của f  x trên đoạn  1  ;2 lớn hơn 5. 
Câu 2. Một xe ô tô đang chạy với vận tốc 65 km / h thì người lái xe bất ngờ phát hiện chướng ngại vật
trên đường cách đó 50 m . Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm
này, ô tô chuyển động chậm dần đều với tốc độ vt   1
 0t  20 m / s, trong đó t là thời gian tính
bằng giây kể từ lúc đạp phanh. Gọi s t  là quảng đường xe ô tô đi được trong t (s) kể từ lúc đạp phanh.
a) Quãng đường s t  mà xe ô tô đi được trong thời gian t (s) là một nguyên hàm của hàm số vt.
b) s t  2  5  t  20t .
c) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 20 s.
d) Xe ô tô đó không va vào chướng ngại vật ở trên đường.
Câu 3. Một kho hàng có 85% sản phẩm loại I và 15% sản phẩm loại II, trong đó có 1% sản phẩm loại I
bị hỏng, 4% sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách
hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
A: “Khách hàng chọn được sản phẩm loại I”, B: “Khách hàng chọn được sản phẩm không bị hỏng”.
a) P A  0,85 .
b) PB | A  0,99 .
c) PB  0,9855 .
d) P A| B  0,95 .
Câu 4. Trong không gian với hệ tọa độ Oxyz, mỗi đơn vị trên trục có độ dài 10 .
km Một trạm theo dõi
được đặt ở gốc tọa độ và có thể phát hiện được các vật thể cách nó một khoảng không quá 30 . km Một vệ  1 7 
tinh do thám di chuyển từ vị trí A4;2;  1 đến vị trí B 1  ; ; 
 với vận tốc 80km | h theo một đường  2 2  thẳng. a) Hai điểm ,
A B nằm ngoài tầm phát hiện của trạm theo dõi.
x  4  2t 
b) Phương trình đường thẳng AB là  y  2  t ,t  . z 1t 
c) Vị trí đầu tiên vệ tinh do thám bị trạm theo dõi phát hiện là M 0;0;  3 .
d) Vệ tinh do thám bay qua vùng bị phát hiện trong khoảng thời gian ít hơn 15 phút.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1.
Cho hình chóp đều S.ABC có SA  a. Gọi D, E lần lượt là trung điểm của S ,
A SC , biết BD 3 a m
vuông góc với AE . Biết thể tích khối chóp S.ABC theo a là
. Tính m  n n
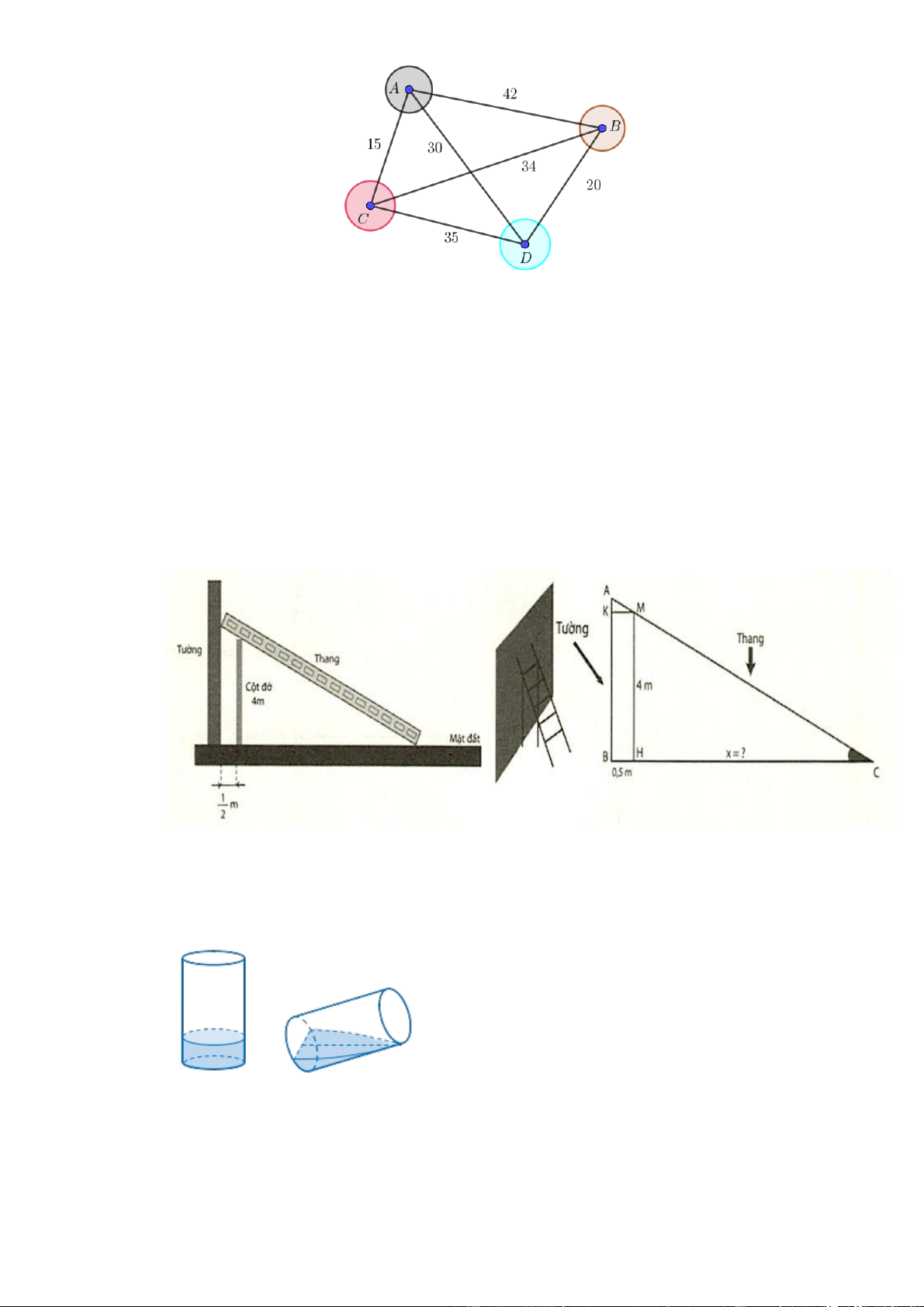
Câu 2. Trường THPT A tổ chức chuyến đi về nguồn cho học sinh tham quan 4 địa điểm A, B, C, D; Thời
gian (đơn vị: phút) di chuyển qua lại giữa các điểm tham quan được mô tả ở hình bên. Đoàn học
sinh của trường sẽ tham quan một địa điểm nào đó đầu tiên, rồi đi qua tất cả các địa điểm còn
lại, mỗi khi đã tham quan địa điểm nào rồi thì sẽ không quay lại đó nữa nhưng phải về địa điểm
ban đầu để trở về. Hỏi tổng thời gian tham quan các địa điểm thỏa mãn điều kiện trên nhận giá
trị nhỏ nhất là bao nhiêu?
Câu 3. Hai chiếc khinh khí cầu cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc khinh khí cầu
thứ nhất cách điểm xuất phát về phía Đông 100km và về phía Nam 80km , đồng thời cách mặt đất
1km. Chiếc khinh khí cầu thứ hai cách điểm xuất phát về phía Bắc 70km và về phía Tây 60km ,
đồng thời cách mặt đất 0,8km . Xác định khoảng cách giữa chiếc khinh khí cầu thứ nhất và chiếc khinh
khí cầu thứ hai ( kết quả làm tròn đến hàng đơn vị).
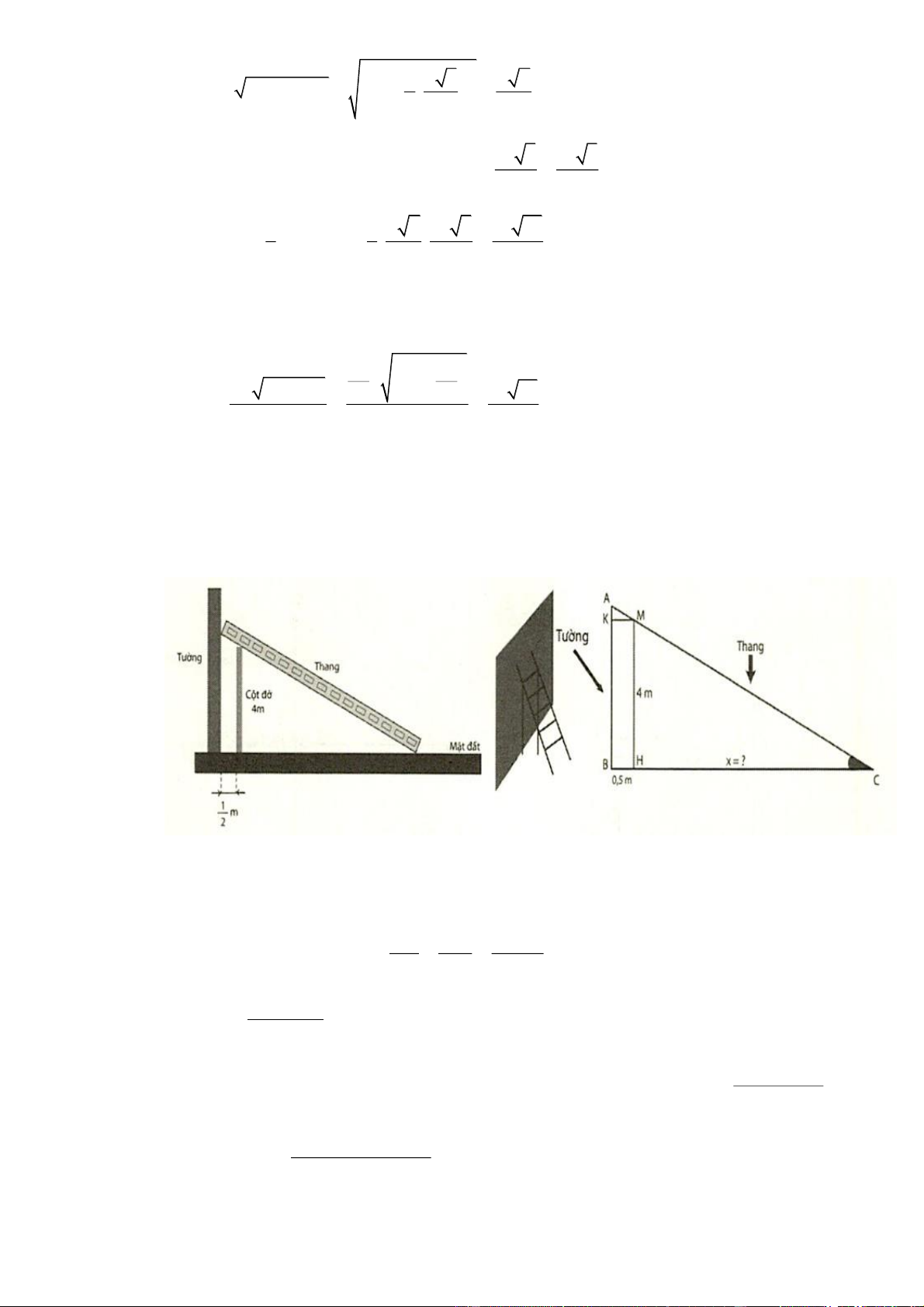
Câu 4. Tìm chiều dài bé nhất của cái thang để nó có thể tựa vào tường và mặt đất, ngang qua cột đỡ cao
4m , song song và cách tường 0,5m kể từ gốc của cột đỡ như hình vẽ (kết quả làm tròn đến hàng phần trăm).
Câu 5. Cho một cái cốc thủy tinh hình trụ bán kính đáy là 6 cm, chiều cao là 10 cm đang đựng một lượng
nước. Tính thể tích lượng nước trong cốc (cm3), biết khi nghiêng cốc nước vừa lúc khi nước chạm miệng
cốc thì ở đáy mực nước trùng với đường kính đáy? (Kết quả được làm tròn đến hàng đơn vị).
Câu 6. Có hai hộp đựng bi: hộp I có 6 viên bi vàng và 4 viên bi đỏ; hộp II có 7 viên bi vàng và 3 viên bi
đỏ. Chọn ngẫu nhiên một viên bi từ hộp I và chuyển nó sang hộp II. Sau đó, chọn ngẫu nhiên một viên bi
từ hộp II. Tính xác suất để viên bi được chọn từ hộp II là viên bi đã được chuyển từ hộp I, biết rằng viên bi
đó là viên bi vàng (làm tròn kết quả đến hàng phần trăm) Đáp án Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C B B B D C C A D C B B Câu 1 Câu 2 Câu 3 Câu 4 a) Đ Đ Đ Đ b) S Đ S Đ c) Đ S Đ S d) Đ Đ S S Câu 1 2 3 4 5 6 Đáp án 75 99 219 5,59 240 0,08 Đúng/Sai 1
Câu 1. Cho hàm số f  x 2
 x  x  6ln x  2. 2
a) Đạo hàm của hàm số là f  x 6 '  x 1 . x  2 b) Trên đoạn  1  ; 
2 , phương trình f ' x  0 có hai nghiệm phân biệt. c) f   1 1  
và f 2  4 12ln 2. 2
d) Giá trị nhỏ nhất của f  x trên đoạn  1  ;2 lớn hơn 5.  Lời giải: a) Đ x 1
b) S f ' x 2
 0  x  3x  4  0   x  4  [ 1;2] c) Đ d) Đ f  f   1 (1) 0; 1  
và f 2  4 12ln 2. 2
Câu 2. Một xe ô tô đang chạy với vận tốc 65 km / h thì người lái xe bất ngờ phát hiện chướng ngại vật
trên đường cách đó 50 m . Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm
này, ô tô chuyển động chậm dần đều với tốc độ vt  1
 0t  20 m / s, trong đó t là thời gian tính
bằng giây kể từ lúc đạp phanh. Gọi s t là quảng đường xe ô tô đi được trong t (giây) kể từ lúc đạp phanh.
a)Quảng đường s t mà xe ô tô đi được trong thời gian t (giây) là một nguyên hàm của hàm số vt .
b) s t  2  5  t  20t .
c) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 20 giây.
d) Xe ô tô đó không va vào chướng ngại vật ở trên đường. Lời giải Do s (
 t)  v(t) nên quãng đường s(t) mà xe ô tô đi được trong thời gian t (giây) là một nguyên hàm của
hàm số v(t) . Ta có: 2 ( 10
 t  20)dt  5
 t  20t  C 
với C là hằng số. Khi đó, ta gọi hàm số 2 s(t)  5
 t  20t  C .
Do s(0)  0 nên C  0 . Suy ra 2 s(t)  5  t  20t .
Xe ô tô dừng hẳn khi v(t)  0 hay 1
 0t  20  0  t  2 . Vậy thời gian kể từ lúc đạp phanh đến khi xe
ô tô dừng hẳn là 2 giây.
Ta có xe ô tô đang chạy với tốc độ 65 km / h 18 m / s .
Do đó, quãng đường xe ô tô còn di chuyển được kể từ lúc đạp phanh đến khi xe dừng hẳn là: 2 s(2)  5  2  202  20( ) m .
Vậy quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến
khi xe ô tô dừng hẳn là: 18  20  38( ) m .
Do 38  50 nên xe ô tô đã dừng hẳn trước khi va chạm với chướng ngại vật trên đường.
Đáp án: a) Đ, b) Đ, c) S, d) Đ.
Câu 3. [NB-TH-TH-VD] Một kho hàng có 85% sản phẩm loại I và 15% sản phẩm loại II, trong đó có
1% sản phẩm loại I bị hỏng, 4% sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như
nhau. Một khách hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
A: "Khách hàng chọn được sản phẩm loại I ";
: "Khách hàng chọn được sản phẩm không bị hỏng".
Các mệnh đề sau đúng hay sai?
a) P A  0,85 .
b) PB | A  0,99 .
c) PB  0,9855 .
d) P A| B  0,95 . Lời giải. a) Đúng b) Đúng c) Đúng d) Sai a) Đúng
Ta có: P A  0,85 . b) Đúng
Ta có: P B | A  1 P B | A 1 0,01 0,99 . c) Đúng
Ta có: P  A   0,15.
P B | A 1 PB | A 1 0,04  0,96
Theo công thức xác suất toàn phần, ta có:
P B  P  A.P B | A  P  A.PB | A  0,85.0,99  0,15.0,96  0,9855 . d) Sai
P A .P B | A 0,85.0, 99
Theo công thức Bayes, ta có: P  A | B        . P  B 0,854 0, 9855
Câu 4. Trong không gian với hệ tọa độ Oxyz, mỗi đơn vị trên trục có độ dài 10 .
km Một trạm theo dõi
được đặt ở gốc tọa độ và có thể phát hiện được các vật thể cách nó một khoảng không quá  1 7  30 .
km Một vệ tinh do thám di chuyển từ vị trí A4;2;  1 đến vị trí B 1  ; ;   với vận tốc  2 2 
80 km | h theo một đường thẳng. a) Hai điểm ,
A B nằm ngoài tầm phát hiện của trạm theo dõi.
x  4  2t 
b) Phương trình đường thẳng AB là  y  2  t ,t  . z 1t 
c) Vị trí đầu tiên vệ tinh do thám bị trạm theo dõi phát hiện là M 0;0;  3 .
d) Vệ tinh do thám bay qua vùng bị phát hiện trong khoảng thời gian ít hơn 15 phút. Lời giải: 3 6 a) OA  21;OB  . ,
A B cách trạm theo dõi lần lượt là10 21  45,8k ;1
m 5 6  36, 7km => Đúng 2 5 5 b) AB  ( 5
 ; ; ) => vectơ chỉ phương của AB là (2;1; 1  ) => Đúng 2 2
c) 30km = 3 đơn vị đọ dài trên trục Phương trình mặt cầu 2 2 2
(S) : x  y  z  9
Toạ độ giao điểm của AB và (S) là M (2;1;2); N(0;0;3)
Vệ tinh đi từ A đến B nên vị trí đầu tiên vệ tinh bị trạm do thám phát hiện là M (2;1;2) => Sai
d) MN  6 . Quãng đường vệ tinh bay trong vùng bị phát hiện là 10 6km nên thời gian
10 6 / 80h  18, 37 phút Sai Trả lời ngắn Câu 1.
Cho hình chóp đều S.ABC có SA  a. Gọi D, E lần lượt là trung điểm của S ,
A SC , biết BD 3 a m
vuông góc với AE . Biết thể tích khối chóp S.ABC theo a là
. Tính m  n n Trả lời: 75 Lời giải S F D E A C B
Gọi F là trung điểm SE  BD  DF ; gọi AB  x 2 2 2 2 2 2 2 2
2AS  2AC  SC
2a  2x  a a  2x 2 2 2
Ta có BE  BD  AE    4 4 4 2 2 2 a  2x a 2   2 2 2 2a 2 2
2BS  2BE  SE 9a  4x 2 2 4 BF    4 4 16 2 5BD 2 2 2 2
BF  BD  DF  BF  4 2 2 2 2 9a  4x 5 a  2x 2 2 2 2 2 2 2   .
 9a  4x  5a 10x  4a  6x  x  a 16 4 4 3
Gọi H là hình chiếu của S lên  ABC khi đó H là tâm đường tròn ngoại tiếp ABC  2  2 x 3  a 7 2 2 2
 SH  SA  AH  a   .    3 2  3   2 2 x 3 a 3
Tam giác ABC đều có cạnh là x  S   ABC  4 6 2 3 1 1 a 7 a 3 a 1 2 Vậy V  SH.S  . .  S . ABC  3 ABC 3 3 6 54
Hoặc sử dụng công thức tính thể tích chóp tam giác ABC đều có cạnh bên bằng a , cạnh đáy bằng x 2 2 2a 2a 2  2 2 2 3a 3
x . 3a  x 3 3 a 21 V    S . ABC 12 12 54
Câu 4. Tìm chiều dài bé nhất của cái thang để nó có thể tựa vào tường và mặt đất, ngang qua cột đỡ cao
4m , song song và cách tường 0,5m kể từ gốc của cột đỡ như hình vẽ (kết quả làm tròn đến hàng phần trăm). Lời giải
Đặt HC  x  0 . Suy ra BC  x  0,5 . HC MH x
Áp dụng định lí Thales, ta có   . BC AB x  0,5 4(x  0, 5) Vậy AB  . x 2 16(x  0,5)
Do tam giác ABC vuông tại B nên suy ra 2 2 2 2
AC  AB  BC  (x  0,5)  . 2 x 2 (x  0, 5)  2 x 16 2  Ra rút ra AC  . 2 x 65 4 3 2 x  x  x 16x  4 Đặt 4 f (x)  (x  0) . 2 x
Bài toán trở thành tìm min f (x) với x  0 . Ta có  65   65  3 2 2 4 3 2 4x  3x 
x 16 x  2x x  x  x 16x  4       2   4  f (x)  4 x 4 3 
2x  x 16x  8  f (x)  . 3 x x  2  0 Vậy 
f  (x)  0  (x  2)(2x 1)  2
x  2x  4  0  1  x    0.  2
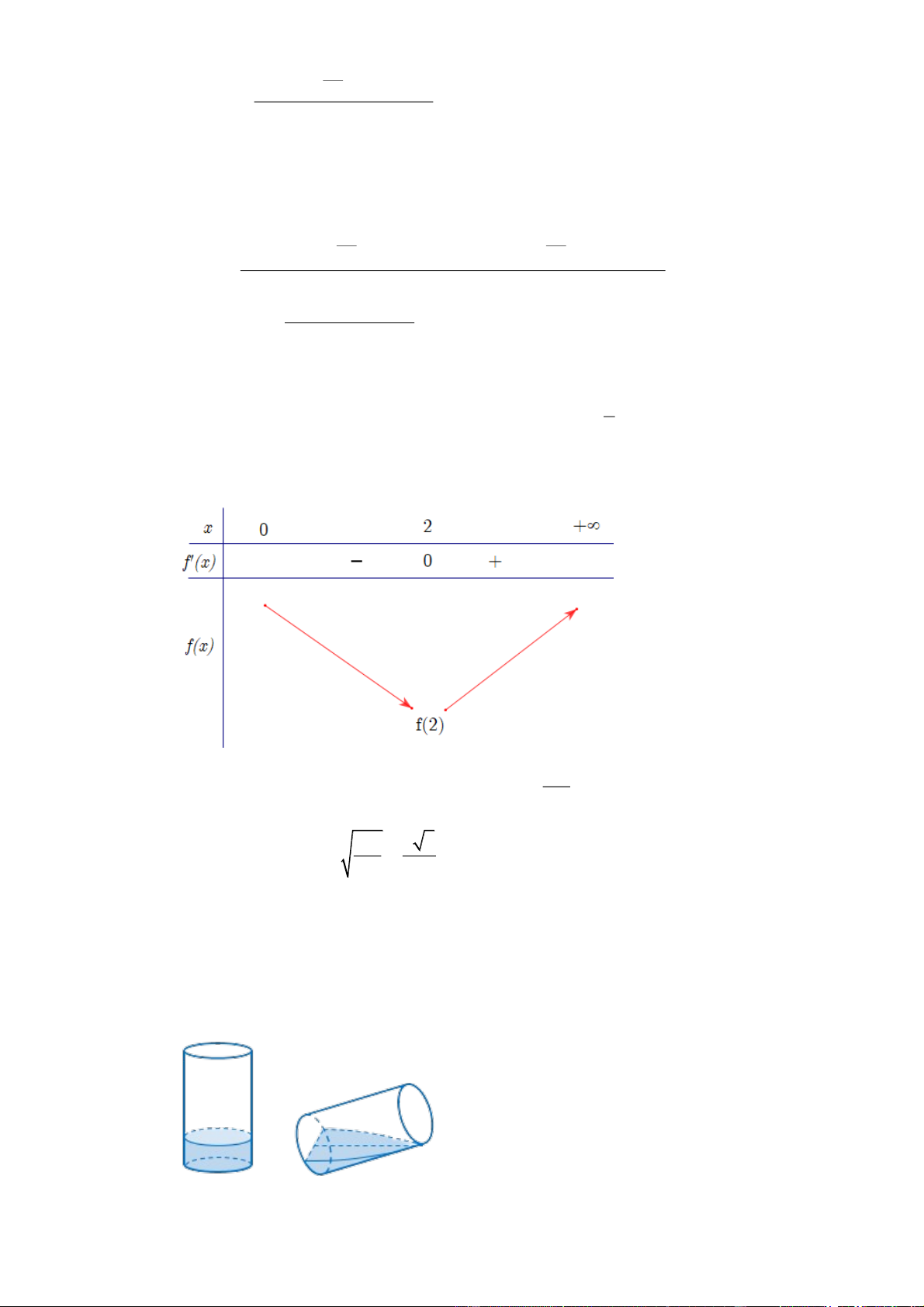
Lập bảng biến thiên, ta có 125
Dựa vào bảng biến thiên, ta có min f (x)  f (2)  . (0;) 4 125 5 5
Do đó, ta có min AC    5,59 . 4 2
Câu 5. Cho một cái cốc thủy tinh hình trụ bán kính đáy là 6 cm, chiều cao là 10 cm đang đựng một lượng
nước. Tính thể tích lượng nước trong cốc, biết khi nghiêng cốc nước vừa lúc khi nước chạm miệng cốc thì
ở đáy mực nước trùng với đường kính đáy? (kết quả được làm tròn đến hàng đơn vị). Hướng dẫn giải
Cốc hình trụ có bán kính R  6 cm, chiều cao h 10 cm.
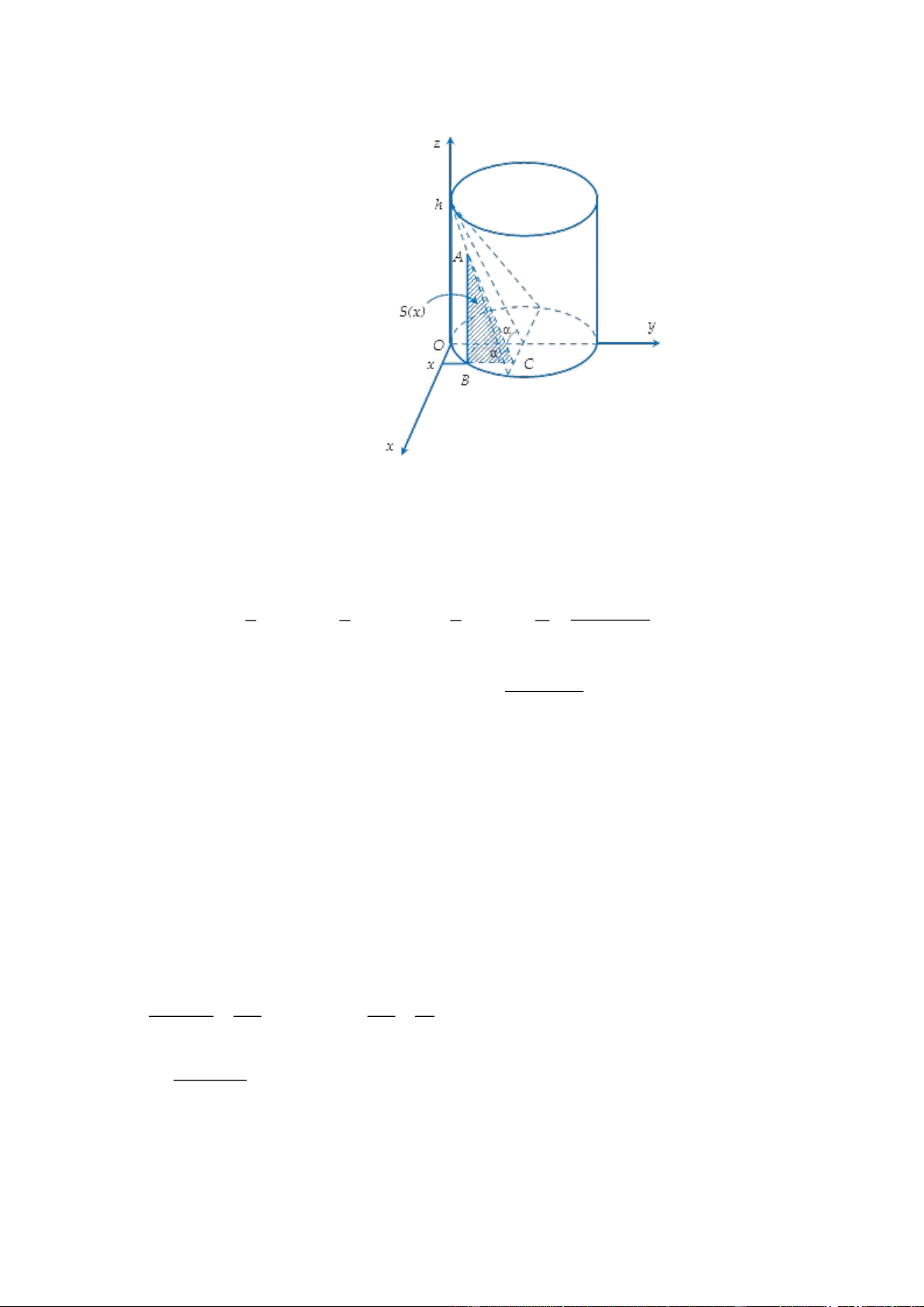
Gán hệ trục tọa độ như hình vẽ bên
Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x ( 6
  x  6 ) cắt vật thể theo thiết diện có diện
tích là S  x .
Ta thấy thiết diện đó là một tam giác ABC vuông tại B như trong hình vẽ.  2 5 36  x  1 1 h
Ta có S  x  1 S  AB  BC 2  BC tan   2 2 R  x   . ABC 2 2 2 R 6 5 2 6 6 36  x 
Vậy thể tích lượng nước trong cốc là V  S
 xdx  dx  240  3 cm . 6 6  6 
Câu 6. Có hai hộp đựng bi: hộp I có 6 viên bi vàng và 4 viên bi đỏ; hộp II có 7 viên bi vàng và 3 viên bi
đỏ. Chọn ngẫu nhiên một viên bi từ hộp I và chuyển nó sang hộp II. Sau đó, chọn ngẫu nhiên một viên bi
từ hộp II. Tính xác suất để viên bi được chọn từ hộp II là viên bi đã được chuyển từ hộp I, biết rằng viên bi
đó là viên bi vàng (làm tròn kết quả đến hàng phần trăm).
Ta có n()  10.11  110
Gọi A à biến cố “lấy được quả bóng từ hộp II mà quả đó được chuyển từ hộp I sang”
C là biến cố “lấy được quả bóng màu vàng từ hộp II” 6.8  4.7 76 6.1 3 P(C)  
; P( A  C)   110 110 110 55
P( A  C)
P( A / C)   0,08 P(C)
Document Outline