16 trang 96 lượt tải

Đề Thi Thử Tốt Nghiệp THPT 2025 Môn Toán Sở GD Quảng Bình Giải Chi Tiết

192

Hai bạn Bảo và Nam của lớp 12A cùng tham gia giải bóng bàn đơn nam do nhà trường tổ chức. Hai bạn đó không cùng một bảng đấu vòng loại và mỗi bảng đấu  vòng loại chỉ chọn một người vào vòng chung kết. Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và bạn Nam. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Chủ đề: Đề thi THPTQG môn Toán năm 2025 385 tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Mỹ Châu

2 tuần trước
Danh sách Quiz
/16
Trang 1
SỞ GD&ĐT
QUẢNG BÌNH
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2025
MÔN: TOÁN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Nguyên hàm của hàm số
5
()f x x
là
A.
6
( ) .
6
x
F x C
B.
6
( ) 5 .F x x C
C.
4
( ) 5 .F x x C
D.
4
( ) .
4
x
F x C
Câu 2. Cho hàm số
liên tục trên . Biết
9
5
( ) 25f x dx
thì
5
9
()f x dx
bằng
A.
9.
B.
5.
C.
25.
D.
25.
Câu 3. Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A.
4,84
. B.
2,10
. C.
2,09
. D.
6,94
.
Câu 4. Trong không gian với hệ trục tọa độ
Oxyz
, cho tam giác
ABC
có ba đỉnh
2;1; 3A
,
4;2;1B
,
3;0;5C
. Tọa độ trọng tâm
G
của tam giác
ABC
là
A.
3;1; 1G
. B.
3;1;1G
. C.
1;3;1G
. D.
1;3;1G
.
Câu 5. Cho hàm số
, 0, 0
ax b
y c ad bc
cx d
có đồ thị như hình bên.
Tiệm cận đứng của đồ thị hàm số đã cho là
A.
1y 
. B.
2y
. C.
1x 
. D.
2x
.
Câu 6. Tập nghiệm của bất phương trình
log 1 1x
là
A.
11; 
. B.
; 11
. C.
11;
. D.
1; 
.
Câu 7. Trong không gian
Oxyz
, cho hai vectơ
1; 2;1a 
và
2; 4; 2b
. Khi đó
.ab
bằng
A.
8
B.
8
C.
12
D.
12
Câu 8. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
M
và
N
theo thứ tự là trung
điểm của cạnh
SA
và
SD
. Mặt phẳng nào sau đây song song với mặt phẳng
MNO
?
Trang 2
A.
SAB
B.
SBC
C.
SCD
D.
SAD
Câu 9. Nghiệm của phương trình
2
log 3x
là:
A.
2
3x
. B.
3
2x
. C.
3x
. D.
2x
.
Câu 10. Cho cấp số nhân
n
u
biết
26
. 64uu
. Giá trị của
35
.uu
bằng:
A.
8
. B.
64
. C.
64
. D.
8
.
Câu 11. Cho hình hộp
.ABCD EFGH
(minh họa như hình bên). Vectơ nào sau đây bằng vectơ
FH
?
A.
DB
. B.
BD
. C.
BA
. D.
AB
.
Câu 12. Cho hàm số có đồ thị như hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
;1
. B.
0;
. C.
1;1
. D.
0;1
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Câu 1. Cho hàm số
( ) sin2f x x x
.
a)
;
2 2 2 2
ff
b) Đạo hàm của hàm số đã cho là
( ) cos2 1f x x

c) Phương trình
( ) 0fx
có hai nghiệm trên đoạn
;
22




là
6
x

và
6
x
.
d) Giá trị nhỏ nhất của hàm số
()y f x
trên đoạn
;
22




là
2
.
A
F
G
H
B
D
C
E
Trang 3
Câu 2. Một sợi dây kim loại dài
6 cm
. Người ta cắt sợi dây đó thành hai đoạn. Đoạn có độ dài
x cm
được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông
0 6 .x
a) Bán kính đường tròn là
2
x
r
.
b) Diện tích hình vuông là
2
6
4
x



.
c) Tổng diện tích hai hình là
2
(4 ) 12 36
16
xx
d) Khi
6
2
x
thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
Câu 3. Hai bạn Bảo và Nam của lớp 12A cùng tham gia giải bóng bàn đơn nam do nhà trường tổ chức. Hai bạn
đó không cùng một bảng đấu vòng loại và mỗi bảng đấu vòng loại chỉ chọn một người vào vòng
chung kết. Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và bạn Nam lần lượt là
0,8
và
0,6
.
Gọi A là biến cố ” Có ít nhất một bạn lọt vào vòng chung kết”.
Gọi B là biến cố “ Chỉ có bạn Bảo lọt vào vòng chung kết”.
a) Xác suất để bạn Nam không lọt vào vòng chung kết là
0,4
.
b) Xác suất để cả hai bạn lọt vào vòng chung kết là
0,8
.
c) Xác suất của biến cố A là
0,48
.
d) Xác suất của biến cố B là
0,32
.
Câu 4. Cho hàm số
32
34y f x x x
a) Hàm số
y f x
nghịch biến trên khoảng
0;2
.
b) Giới hạn
lim
x
fx


.
c) Gọi
,AB
lần lượt là hai điểm cực trị của hàm số. Khi đó độ dài
AB
bằng
5
.
d) Đồ thị hàm số
1x
y
fx
có đúng hai đường tiệm cận đứng.
PHẦN III. Thí sinh trả lời từ câu 19 đến câu 22
Câu 1. Cho hình chóp tứ giác đều
.S ABCD
, có cạnh đáy bằng 2, cạnh bên bằng
22
. Tính khoảng cách
giữa hai đường thẳng
AB
và
SD
(kết quả làm tròn đến hàng phần mười)
Câu 2. Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hinh vẽ bên durớt). Chi phí di
chuyển giữa các thảnh phố được mô tả trên hình (đơn vi tinh: triệu đồng). Xe giao hàng cưa công ty xuất
phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần sau đó
trở lại thành phố ban đầu. Tìm chi phí thấp nhất cùa xe giao hàng.
Trang 4
Câu 3. Một máy bay không người lái bay lên tại 1 điểm. Sau một thời gian bay, cách điểm xuất phát về phía Bắc
50 km
và về phía Tây
20 km
, đồng thời cách mặt đất
1 km
. Lúc đó máy bay cách vị trí tại điểm
xuất phát của nó là
a km
, giá trị cùa
a
là bao nhiêu? ( kết quả làm tròn đến hàng phần mười).
Câu 4. Cho
fx
là hàm số liên tục trên , biết
2
32
1
16 15 2 21f x x x x f t t
d
. Giá trị của
2f
bằng bao nhiêu?
Câu 5. Người ta muốn lắp đặt một ống dẫn dầu từ nhà máy lọc dầu ở vị trí A đến kho chứa dầu đặt ở vị trí B qua
một con sông rộng
2km
, dài
6km
. Chi phí lắp đặt đường ống dẫn dầu trên mặt đất để nối từ nhà máy lọc
dầu đến trạm trung chuyển tại vị trí P là
4
tỷ VNĐ/ 1km và chi phí lắp đặt ống dẫn dầu dưới dòng sông để
nối từ P đến kho chứa dầu tại vị trí B là 8 tỷ VNĐ/1km (như hình vẽ dưới). Hỏi để chi phí lắp đặt ít nhất
cần
đặt vị trí P cách nhà máy lọc dầu là bao nhiêu kilômét? (làm tròn kết quả đến hàng phần trăm)
Câu 6. Trong đợt củng hộ sách giáo khoa cho những học sinh bị ảnh hưởng do trận lũ lụt vừa qua, lớp 12A nhận
được
20
cuốn sách gồm
5
cuốn sách toán học,
7
cuốn sách Vật lí,
8
cuốn sách Hóa học, các sách cùng
môn học là giống nhau. Số sách này được chia đều cho 10 học sinh, mỗi học sinh chỉ được nhận đúng 2
cuốn sách khác môn học. Trong số
10
học sinh nhận sách đợt này có bạn Hưng và bạn Thành. Tính xác
suất để 2 cuốn sách mà bạn Hưng nhận đươc giống
2
cuốn sách của bạn Thành (làm tròn kết quả đến
hàng phần trăm)
HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Nguyên hàm của hàm số
5
()f x x
là
A.
6
( ) .
6
x
F x C
B.
6
( ) 5 .F x x C
C.
4
( ) 5 .F x x C
D.
4
( ) .
4
x
F x C
9
14
13
11
10
8
12
14
A
B
C
D
E
Trang 5
Lời giải
Áp dụng công thức, ta có nguyên hàm của
5
()f x x
là:
5 1 6
5
()
5 1 6
xx
F x x dx C C
.
Vậy đáp án đúng là A.
Câu 2. Cho hàm số
()y f x
liên tục trên . Biết
9
5
( ) 25f x dx
thì
5
9
()f x dx
bằng
A.
9.
B.
5.
C.
25.
D.
25.
Lời giải
Ta có:
95
59
( ) 25 ( ) 25.f x dx f x dx

Câu 3. Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A.
4,84
. B.
2,10
. C.
2,09
. D.
6,94
.
Lời giải
Cỡ mẫu:
3 8 7 12 7 1 1 39n
.
2 20
Qx
1 10
4;5Qx
1
39
3
155
4
4 .1 4,84375
8 32
Q
.
Câu 4. Trong không gian với hệ trục tọa độ
Oxyz
, cho tam giác
ABC
có ba đỉnh
2;1; 3A
,
4;2;1B
,
3;0;5C
. Tọa độ trọng tâm
G
của tam giác
ABC
là
A.
3;1; 1G
. B.
3;1;1G
. C.
1;3;1G
. D.
1;3;1G
.
Lời giải
Trọng tâm
G
của tam giác
ABC
là
3;1;1G
.
Câu 5. Cho hàm số
, 0, 0
ax b
y c ad bc
cx d
có đồ thị như hình bên.
Trang 6
Tiệm cận đứng của đồ thị hàm số đã cho là
A.
1y 
. B.
2y
. C.
1x 
. D.
2x
.
Lời giải
Dựa vào đồ thị ta có tiệm cận đứng của đồ thị hàm số là
2x
.
Câu 6. Tập nghiệm của bất phương trình
log 1 1x
là
A.
11; 
. B.
; 11
. C.
11;
. D.
1; 
.
Lời giải
Ta có
1
log 1 1 1 10 11x x x
.
Câu 7. Trong không gian
Oxyz
, cho hai vectơ
1; 2;1a 
và
2; 4; 2b
. Khi đó
.ab
bằng
A.
8
B.
8
C.
12
D.
12
Lời giải
Ta có
. 1.2 2 . 4 1. 2 8ab
.
Câu 8. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
M
và
N
theo thứ tự là
trung điểm của cạnh
SA
và
SD
. Mặt phẳng nào sau đây song song với mặt phẳng
MNO
?
A.
SAB
B.
SBC
C.
SCD
D.
SAD
Lời giải
Vì
ABCD
là hình bình hành nên
O
là trung điểm của
AC
và
BD
. Lại có
M
và
N
theo thứ tự là
trung điểm của
SA
và
SD
//OM SC
và
//ON SB
//OMN SBC
.
Câu 9. Nghiệm của phương trình
2
log 3x
là:
A.
2
3x
. B.
3
2x
. C.
3x
. D.
2x
.
O
A
D
B
C
S
N
M
Trang 7
Lời giải
Ta có:
3
2
log 3 2xx
.
Câu 10. Cho cấp số nhân
n
u
biết
26
. 64uu
. Giá trị của
35
.uu
bằng:
A.
8
. B.
64
. C.
64
. D.
8
.
Lời giải
Gọi
q
là công bội của cấp số nhân
n
u
. Ta có
2 6 2 4
2 6 1 1 1 3 5
. . . . . . 64u u u q u q u q u u
Câu 11. Cho hình hộp
.ABCD EFGH
(minh họa như hình bên). Vectơ nào sau đây bằng vectơ
FH
?
A.
DB
. B.
BD
. C.
BA
. D.
AB
.
Lời giải
Nhận xét: Tứ giác
BDHF
là hình bình hành nên
BD FH
.
Câu 12. Cho hàm số có đồ thị như hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
;1
. B.
0;
. C.
1;1
. D.
0;1
.
Lời giải
Nhận xét: Trên khoảng
0;1
nhìn từ trái qua phải đồ thị đi lên nên hàm số đồng biến.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Câu 1: [ NB-TH-TH-TH] Cho hàm số
sin2f x x x
.
a)
;
2 2 2 2
ff
.
b) Đạo hàm của hàm số đã cho là
' cos2 1f x x
.
A
F
G
H
B
D
C
E
Trang 8
c) Phương trình
0fx
có hai nghiệm trên đoạn
;
22




là
6
x

và
6
x
.
d) Giá trị nhỏ nhất của hàm số
y f x
trên đoạn
;
22




là
2
.
Lời giải
Đáp án:
Câu 1
a. Đúng
b. Sai
c. Đúng
d. Đúng
a)
;
2 2 2 2
ff
.
Ta có:
sin ; sin
2 2 2 2 2 2
ff

.
Chọn Đúng
b) Đạo hàm của hàm số đã cho là
cos2 1f x x

.
Ta có:
sin 2 2cos2 1f x x x x
.
Chọn Sai.
c) Phương trình
0fx
có hai nghiệm trên đoạn
;
22




là
6
x

và
6
x
.
Ta có:
1
0 2cos2 1 0 cos2 cos 2 2
2 3 3
f x x x x k

6
x k k
.
Do
;
22
x




nên
6
x

và
6
x
.
Chọn Đúng.
d) Giá trị nhỏ nhất của hàm số
y f x
trên đoạn
;
22




là
2
.
Trang 9
1
0 2cos2 1 0 cos2 cos 2 2
2 3 3 6
f x x x x k x k

Do
;
22
x




nên
6
x

và
6
x
.
Mà :
1,57
22
1,57
22
3
0,34
6 2 6
3
0,34
6 2 6
f
f
f
f

















Suy ra giá trị nhỏ nhất của hàm số
y f x
trên đoạn
;
22




là
2
.
Chọn Đúng
Câu 2. [ NB-TH-TH-VD] Một sợi dây kim loại dài
6 cm
. Người ta cắt sợi dây đó thành hai đoạn. Đoạn
có độ dài
x cm
được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông
06x
.
a) Bán kính đường tròn là
x
r
.
b) Diện tích hình vuông là
2
6
4
x



.
c) Tổng diện tích hai hình là
2
4 . 12 36
16
xx
.
d) Khi
6
2
x
thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
Lời giải
a) Sai
b) Đúng
c) Đúng
d) Sai
a) Đúng.
Do chu vi của đường tròn là
x cm
nên bán kính đường tròn là
2
x
r
.
b) Đúng.
Chu vi của hình vuông là:
6 0 6x cm x
Độ dài một cạnh của hình vuông là:
6
4
x
cm
Diện tích hình vuông là:
2
6
4
x



.
Trang 10
c) Đúng.
Tổng diện tích của 2 hình là:
22
22
2
2
22
6 36 12
..
2 4 4 16
4 12 36
4 36 12
16 16
x x x x x
xx
x x x




d) Đúng.
Xét hàm số
2
4 12 36
, 0 6
16
xx
yx
1
. 2. 4 12
16
yx



12 6
0
2. 4 4
yx



BBT:
Vậy tổng diện tích của hai hình bé nhất khi
6
4
x
Câu 3. Hai bạn Bảo và Nam của lớp 12A cùng tham gia giải bóng bàn đơn nam do nhà trường tổ chức.
Hai bạn đó không cùng một bảng đấu vòng loại và mỗi bảng đấu vòng loại chỉ chọn một người
vào vòng chung kết. Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và bạn
Nam lần lượt là
0,8
và
0,6
.
Gọi A là biến cố ” Có ít nhất một bạn lọt vào vòng chung kết”.
Gọi B là biến cố “ Chỉ có bạn Bảo lọt vào vòng chung kết”.
a) [NB] Xác suất để bạn Nam không lọt vào vòng chung kết là
0,4
.
b) [TH] Xác suất để cả hai bạn lọt vào vòng chung kết là
0,8
.
c) [TH] Xác suất của biến cố A là
0,48
.
d) [VD] Xác suất của biến cố B là
0,32
.
Lời giải
Đáp số: a) Đúng; b) Sai; c)Sai; d)Đúng.
a) [NB] Đúng vì: Xác suất để bạn Nam lọt vào vòng chung kết là
0,6
.
Xác suất để bạn Nam không lọt vào vòng chung kết là
1 0,6 0,4
.
b) [TH] Sai vì:
Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và Nam lần lượt là
0,8
và
0,6
.
Xác suất để cả hai bạn lọt vào vòng chung kết là
0,8.0,6 0,48
.
c) [TH] Sai vì:
Trang 11
Ta có xác suất để cả hai bạn không lọt vào vòng chung kết là
1 0,8 . 1 0,6 0,08
.
Xác suất của biến cố A là
1 0,08 0,92
.
d) [VD] Đúng vì:
Xác suất để chỉ có bạn Bảo lọt vào vòng chung kết là
0,8. 1 0,6 0,32
Xác suất của biến cố B là
0,32
.
Câu 4. Cho hàm số
32
34y f x x x
a) Hàm số
y f x
nghịch biến trên khoảng
0;2
.
b) Giới hạn
lim
x
fx


.
c) Gọi
,AB
lần lượt là hai điểm cực trị của hàm số. Khi đó độ dài
AB
bằng
5
.
d) Đồ thị hàm số
1x
y
fx
có đúng hai đường tiệm cận đứng.
Lời giải
a) Đúng, vì:
+ Tập xác định của hàm số
y f x
là:
D
.
+
2
36y x x

.
+
2
0
0 3 6 0
2
x
y x x
x
.
+ Bảng xét dấu:
+ Vậy hàm số
y f x
nghịch biến trên khoảng
0;2
.
b) Đúng, vì:
+
3 2 3
3
34
lim lim 3 4 lim 1
x x x
f x x x x
xx
  




.
c) Sai, vì:
+ Tọa độ điểm cực trị:
0;4 , 2;0AB
+
25AB
.
d) Sai, vì:
+ Xét hàm số
32
11
34
xx
y
f x x x



.
+ Tập xác định:
\ 1;2D 
.
+ Trường hợp 1:
Trang 12
3 2 2
22
1 1 1 1
1 1 1 1 1
lim lim lim lim
3 4 4 4 9
1 4 4 1 4 4
x x x x
x x x
x x x x
x x x x x x
 
.
Nên trường hợp này, đồ thị của hàm số không có tiệm cận đứng.
+ Trường hợp 2:
3 2 3 2
22
11
lim ; lim
3 4 3 4
xx
xx
x x x x



 
Nên trường hợp này, đồ thị của hàm số nhận
2x
làm tiệm cận đứng.
PHẦN III. Thí sinh trả lời từ câu 19 đến câu 22
Câu 1: Cho hình chóp tứ giác đều
.S ABCD
, có cạnh đáy bằng 2, cạnh bên bằng
22
.
Tính khoảng cách giữa hai đường thẳng
AB
và
SD
(kết quả làm tròn đến hàng phần mười)
Lời giải
Đáp án: 1,8
Chọn hệ trục tọa độ như hình vẽ, ta có
2;0;0 ; 0; 2;0 , 0; 2;0A B D
,
0;0; 6S
.
Đường thẳng
AB
qua
A
và có vecto chỉ phương
2; 2;0AB 
Đường thẳng SD qua
D
và có vecto chỉ phương
0; 2; 6SD 
2; 2;0 .AD
, 2 ;2 3;23 .AB SD


;
2 6 2 6 0
42
; 1,8
12 12 4
;
66
2 7 7
AD AB SD
d AB SD
AB SD






.
Câu 2: Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hinh vẽ bên durớt). Chi phí di
chuyển giữa các thảnh phố được mô tả trên hình (đơn vi tinh: triệu đồng). Xe giao hàng cưa công ty
xuất phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần
sau đó trở lại thành phố ban đầu. Tìm chi phí thấp nhất cùa xe giao hàng.
2
x
y
z
2
2
O
B
A
D
C
S
Trang 13
Lời giải
Đáp án: 53
Đường đi
Tống số chi phí
A B C E D A
9 14 12 14 11 60
A B E C D A
9 8 12 13 11 53
A E B C D A
10 8 14 13 11 56
A E D C B A
10 14 13 14 9 60
A D C E B A
11 13 12 8 9 53
A D E C B A
11 14 12 14 9 60
A B C D E A
9 14 13 14 10 60
A D C B E A
11 13 14 8 10 56
Vậy chi phí nhỏ nhất của xe giao hàng là 53.
Câu 3. Một máy bay không người lái bay lên tại 1 điểm. Sau một thời gian bay, cách điểm xuất phát về
phía Bắc
50 km
và về phía Tây
20 km
, đồng thời cách mặt đất
1 km
. Lúc đó máy bay cách
vị trí tại điểm xuất phát của nó là
a km
, giá trị cùa
a
là bao nhiêu? ( kết quả làm tròn đến
hàng phần mười).
Lời giải
Đáp án:
53,9
.
Chọn hệ trục toạ độ sao cho vị trí ban đầu của máy bay là
0;0;0O
, vị trí cần tính là
20;50;1A
. Khi đó độ dài
AB
là khoảng cách của máy bay đến điểm xuất phát.
Nên
2 2 2
20 50 1 2901 53,9AB a
9
14
13
11
10
8
12
14
A
B
C
D
E
Trang 14
Câu 4. Cho
fx
là hàm số liên tục trên , biết
2
32
1
16 15 2 21f x x x x f t t
d
. Giá trị của
2f
bằng bao nhiêu?
Lời giải
Đáp án:
39
.
Giả sử
2
1
f t t a
d
và
32
16 15 2 21f x x x ax
.
Khi đó ta có:
2 2 2
3 2 3 2
1 1 1
16 15 2 21 2 16 15 21 3 4 2t t at t a at t t t t a a a
d d d
.
Do đó:
32
16 15 4 21f x x x x
nên
2 39f
.
Câu 5. Người ta muốn lắp đặt một ống dẫn dầu từ nhà máy lọc dầu ở vị trí A đến kho chứa dầu đặt ở vị
trí B qua một con sông rộng
2km
, dài
6km
. Chi phí lắp đặt đường ống dẫn dầu trên mặt đất để
nối từ nhà máy lọc dầu đến trạm trung chuyển tại vị trí P là
4
tỷ VNĐ/ 1km và chi phí lắp đặt
ống dẫn dầu dưới dòng sông để nối từ P đến kho chứa dầu tại vị trí B là 8 tỷ VNĐ/1km (như
hình vẽ dưới ). Hỏi để chi phí lắp đặt ít nhất cần đặt vị trí P cách nhà máy lọc dầu là bao nhiêu
kilômét? (làm tròn kết quả đến hàng phần trăm)
Lời giải
Đáp số:
4,85
Đặt
, 0 6AP x km x
.Khi đó
2
22
6 2 12 40PB x x x
Chi chí lắp đặt ống dẫn là:
2
4 8 12 40C x x x x
(tỷ)
2
2
4 2 12
18 2 3
4 , 0 12 40 12 2 0;6
3
12 40
x
C x C x x x x x
xx


Trang 15
18 2 3
0 16 10, 6 40, 24 8 3
3
C C C




0;6
18 2 3
min 24 8 3
3
C x C




Vậy chi phí lắp đặt ít nhất khi đặt vị trí
P
cách nhà máy lọc dầu
18 2 3
4,85
3
km
Câu 6. Trong đợt củng hộ sách giáo khoa cho những học sinh bị ảnh hưởng do trận lũ lụt vừa qua, lớp
12A nhận được
20
cuốn sách gồm
5
cuốn sách toán học,
7
cuốn sách Vật lí,
8
cuốn sách Hóa
học, các sách cùng môn học là giống nhau. Số sách này được chia đều cho 10 học sinh, mỗi học
sinh chỉ được nhận đúng 2 cuốn sách khác môn học. Trong số
10
học sinh nhận sách đợt này
có bạn Hưng và bạn Thành. Tính xác suất để 2 cuốn sách mà bạn Hưng nhận đươc giống
2
cuốn sách của bạn Thành (làm tròn kết quả đến hàng phần trăm)
Lời giải
Đáp số:
0,31
Cách 1
Gọi
x
là số học sinh nhận sách Toán và Lí
y
là số học sinh nhận sách Lí và Hóa
z
là số học sinh nhận sách Hóa và Toán
Theo bài ra ta có hệ;
72
85
53
x y x
y z y
z x z





Ta chia 20 cuốn sách thành 10 bộ trong đó có 2 bộ sách Toán và Lí,
5
bộ sách Lí và Hóa,
3
bộ Toán
và Hóa được trao.
Bạn Thành và Hưng nhận
2
bộ sách trong số
10
bộ được trao
+) Số phần tử của không gian mẫu:
2
10
45nC
+) Gọi A là biến cố; “Hưng nhận
2
cuốn sách giống bạn Thành”
TH1: Thành và Hưng nhận sách Toán và Lí có
2
2
C
cách
TH2: Thành và Hưng nhận sách Hóa và Lí có
2
5
C
cách
TH3: Thành và Hưng nhận sách Toán và Hóa có
2
3
C
cách
222
2 5 3
14n A C C C
+) Xác suất của biến cố A là:
14
0,31
45
PA
Cách 2:
Gọi
x
là số học sinh nhận sách Toán và Lí
y
là số học sinh nhận sách Lí và Hóa
z
là số học sinh nhận sách Hóa và Toán
Trang 16
Theo bài ra ta có hệ;
72
85
53
x y x
y z y
z x z





+) Số phần tử của không gian mẫu :
5 3 2
10 5 2
. . 2520n C C C
+) Gọi
A
là biến cố: “Hưng nhận
2
cuốn sách giống bạn Thành”
TH1: Thành và Hưng nhận sách Toán và Lí có
53
83
1. . 56CC
cách
TH2: Thành và Hưng nhận sách Hóa và Lí có
3 3 2
8 5 2
1. . . 560CCC
cách
TH3: Thành và Hưng nhận sách Toán và Hóa có
1 5 2
8 7 2
1. . . 168C C C
cách
56 560 168 784nA
+) Xác suất của biến cố
A
là:
784
0,31
2520
PA

Tài liệu khác của Toán

Preview text:

SỞ GD&ĐT
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2025 QUẢNG BÌNH MÔN: TOÁN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Nguyên hàm của hàm số 5
f (x)  x là 6 x 4 x
A. F (x)   C. B. 6
F(x)  5x  . C C. 4
F(x)  5x  . C
D. F (x)   C. 6 4 9 5
Câu 2. Cho hàm số y f (x) liên tục trên . Biết
f (x)dx  25  thì f (x)dx  bằng 5 9 A. 9. B. 5. C. 25. D. 25. 
Câu 3. Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là A. 4,84 . B. 2,10 . C. 2, 09 . D. 6,94 .
Câu 4. Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC có ba đỉnh A2;1;  3 , B4;2;  1 ,
C 3;0;5. Tọa độ trọng tâm G của tam giác ABC là
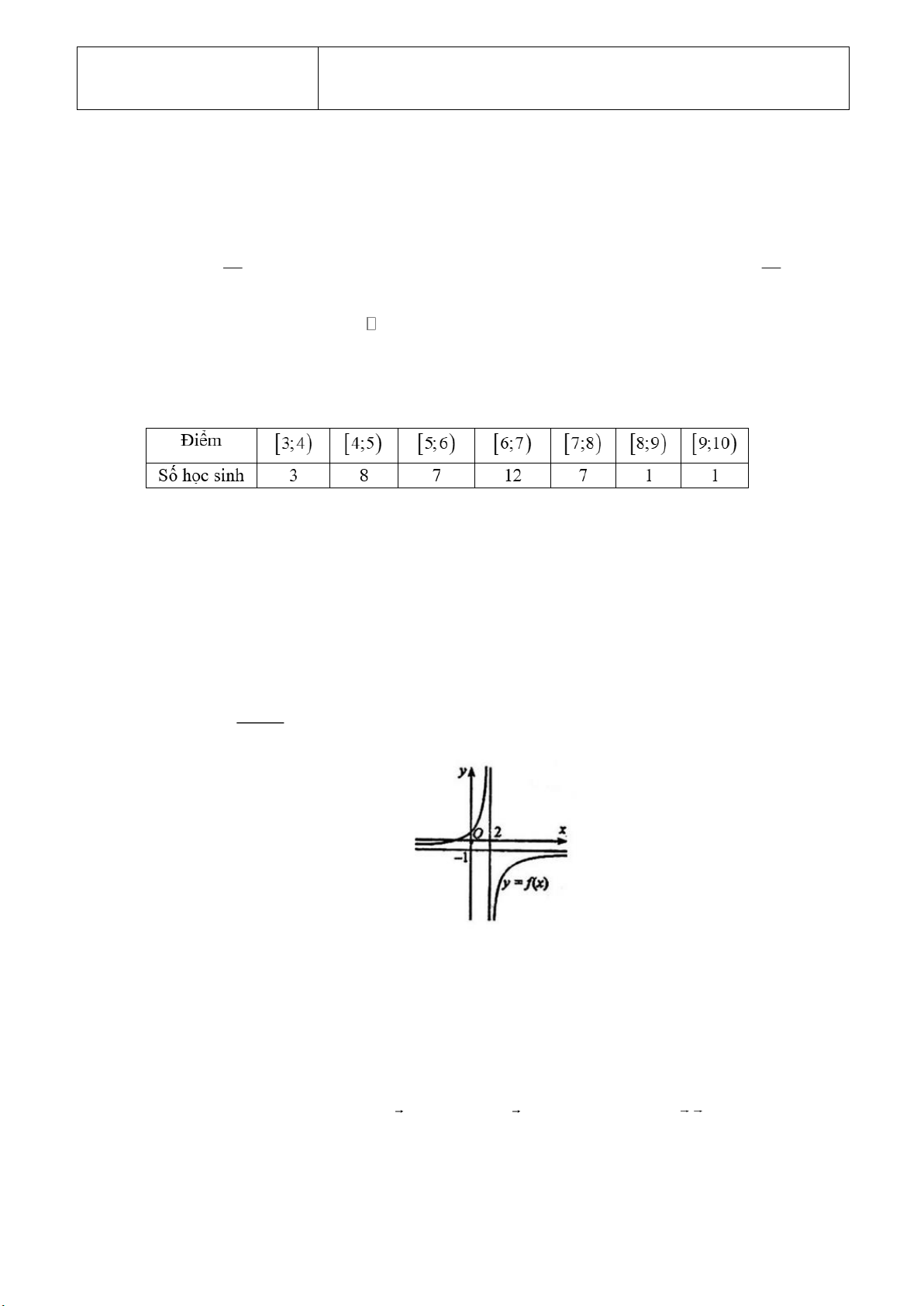
A. G3;1;  1 . B. G 3;1;  1 . C. G 1;3;  1 . D. G 1  ;3;  1 . ax b
Câu 5. Cho hàm số y
, c  0, ad bc  0 cx
có đồ thị như hình bên. d
Tiệm cận đứng của đồ thị hàm số đã cho là A. y  1  .
B. y  2 . C. x  1  . D. x  2 .
Câu 6. Tập nghiệm của bất phương trình log  x   1 1 là
A. 11;   . B.  ;  1  1 .
C. 11;  .
D. 1;  .
Câu 7. Trong không gian Oxyz , cho hai vectơ a  1; 2   ;1 và b  2; 4  ; 2  . Khi đó . a b bằng A. 8 B. 8  C. 12 D. 12 
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M và N theo thứ tự là trung
điểm của cạnh SA và SD . Mặt phẳng nào sau đây song song với mặt phẳng MNO ? Trang 1
A. SAB
B.SBC
C.SCD D.SAD
Câu 9. Nghiệm của phương trình log x  3 là: 2 A. 2 x  3 . B. 3 x  2 .
C. x  3. D. x  2 .
Câu 10. Cho cấp số nhân u biết u .u  64 . Giá trị của u .u bằng: n  2 6 3 5 A. 8  . B. 64  . C. 64 . D. 8 .
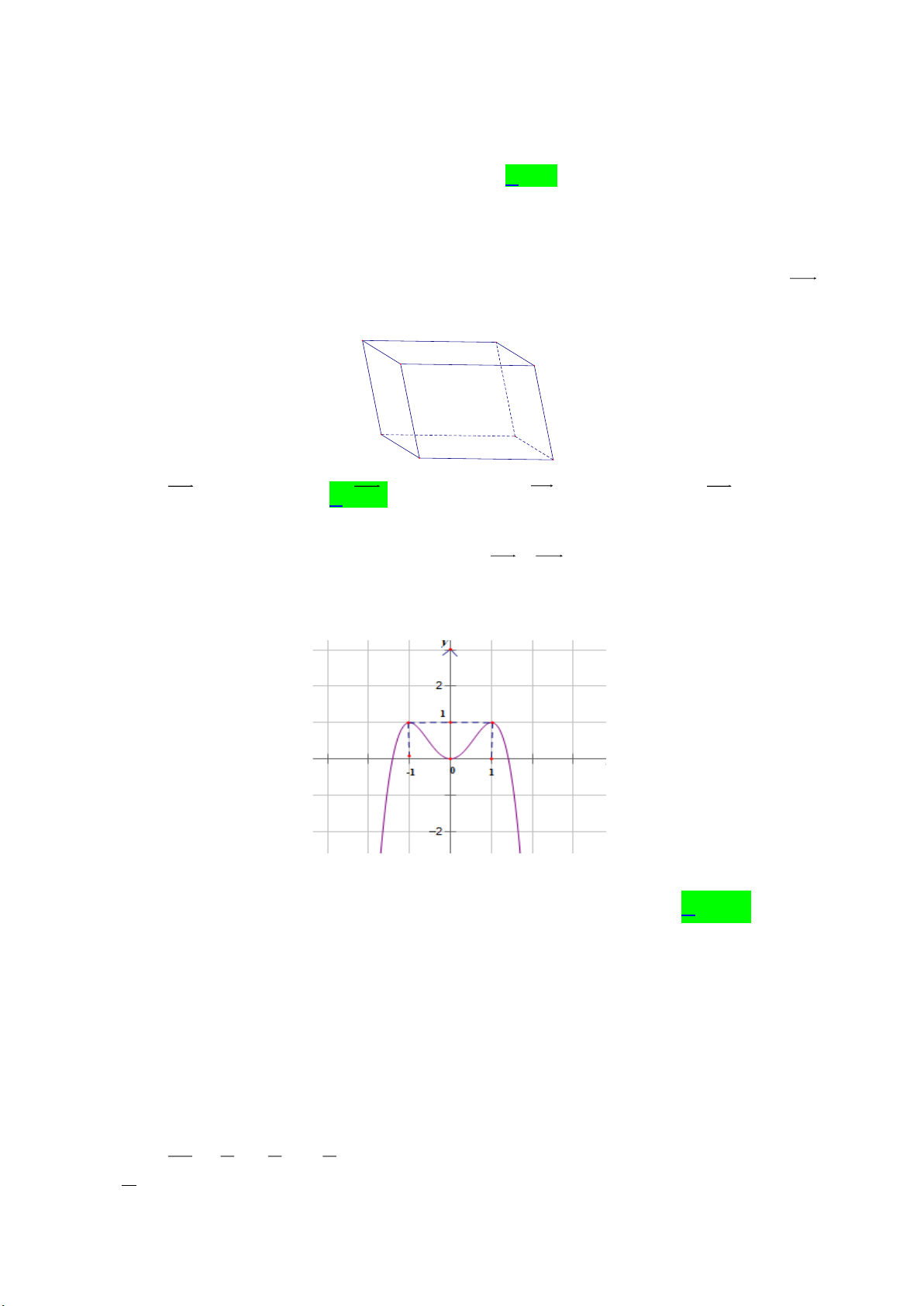
Câu 11. Cho hình hộp ABC .
D EFGH (minh họa như hình bên). Vectơ nào sau đây bằng vectơ FH ? A B D C F E H G A. DB . B. BD . C. BA . D. AB .
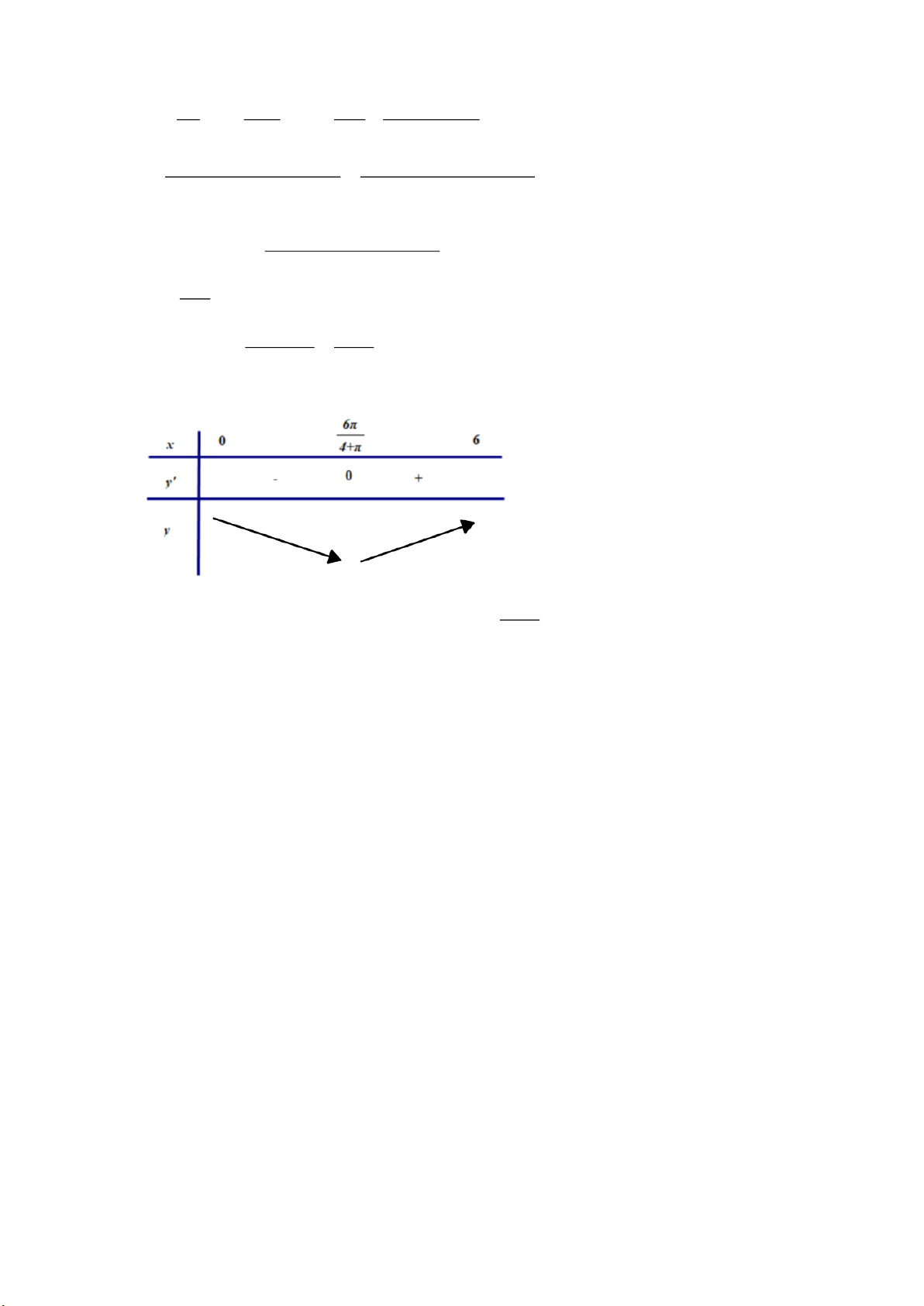
Câu 12. Cho hàm số có đồ thị như hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.   ;1  . B. 0; . C.  1  ;  1 . D. 0;  1 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Câu 1. Cho hàm số f (x)  sin 2x x .         a) f   ; f        2  2  2  2 b) Đạ 
o hàm của hàm số đã cho là f (x)  cos 2x 1      
c) Phương trình f (x)  0 có hai nghiệm trên đoạn  ; 
 là x   và x  .  2 2  6 6     
d) Giá trị nhỏ nhất của hàm số y f (x) trên đoạn  ;   là  .  2 2  2 Trang 2
Câu 2. Một sợi dây kim loại dài 6cm . Người ta cắt sợi dây đó thành hai đoạn. Đoạn có độ dài  xcm
được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông 0  x  6. a) Bán kính đườ x ng tròn là r  . 2 2  6  x
b) Diện tích hình vuông là   .  4  2
(4   )x 12 x  36
c) Tổng diện tích hai hình là 16 6 d) Khi x
thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất. 2  
Câu 3. Hai bạn Bảo và Nam của lớp 12A cùng tham gia giải bóng bàn đơn nam do nhà trường tổ chức. Hai bạn
đó không cùng một bảng đấu vòng loại và mỗi bảng đấu vòng loại chỉ chọn một người vào vòng
chung kết. Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và bạn Nam lần lượt là 0,8 và 0, 6 .
Gọi A là biến cố ” Có ít nhất một bạn lọt vào vòng chung kết”.
Gọi B là biến cố “ Chỉ có bạn Bảo lọt vào vòng chung kết”.
a) Xác suất để bạn Nam không lọt vào vòng chung kết là 0, 4 .
b) Xác suất để cả hai bạn lọt vào vòng chung kết là 0,8 .
c) Xác suất của biến cố A là 0, 48 .
d) Xác suất của biến cố B là 0, 32 .
y f x 3 2
x 3x  4 Câu 4. Cho hàm số 0;2
a) Hàm số y f x nghịch biến trên khoảng .
lim f x  
b) Giới hạn x . c) Gọi ,
A B lần lượt là hai điểm cực trị của hàm số. Khi đó độ dài AB bằng 5 . x 1
y f x d) Đồ thị hàm số
có đúng hai đường tiệm cận đứng.
PHẦN III. Thí sinh trả lời từ câu 19 đến câu 22
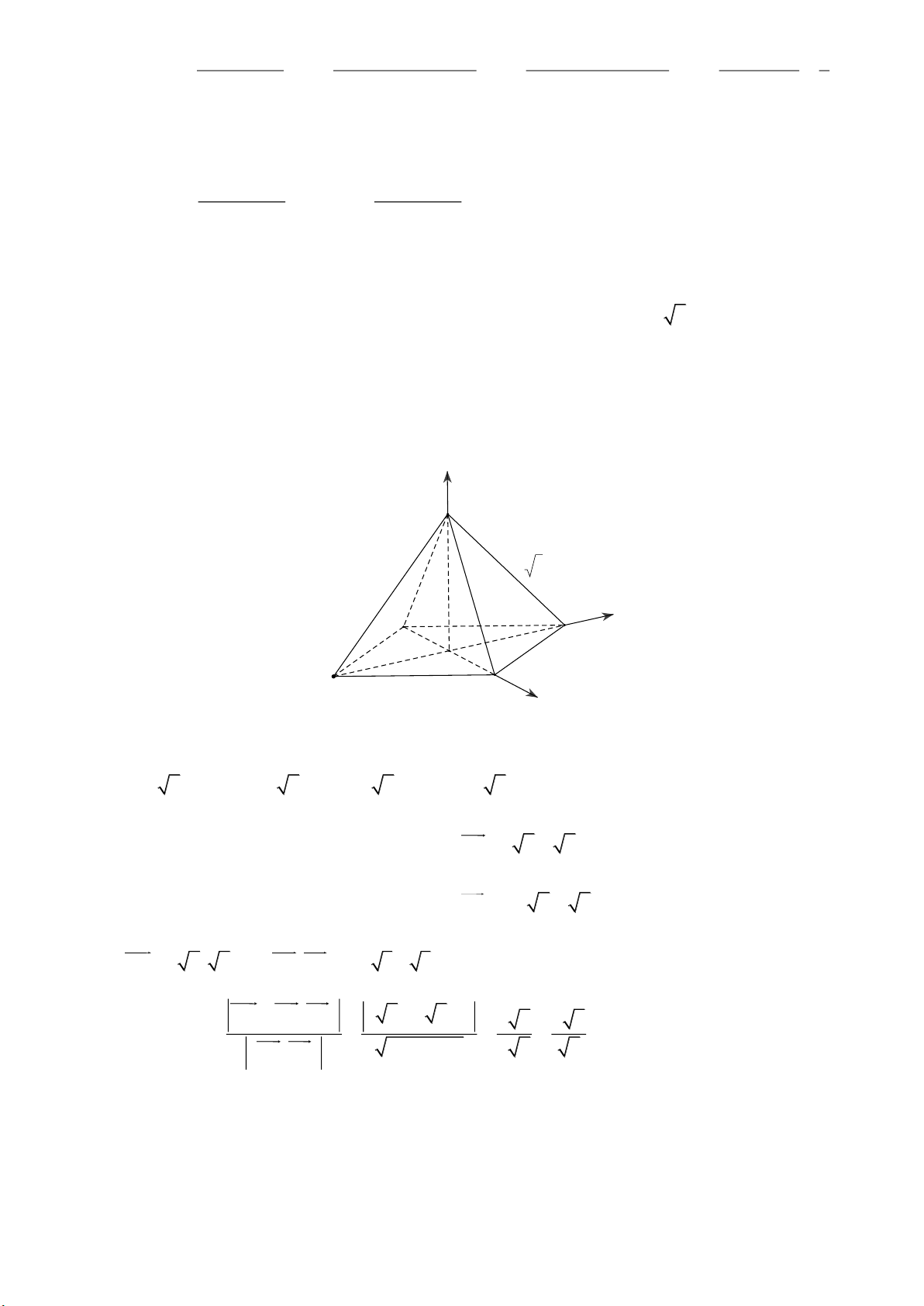
Câu 1. Cho hình chóp tứ giác đều S.ABCD , có cạnh đáy bằng 2, cạnh bên bằng 2 2 . Tính khoảng cách
giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười)
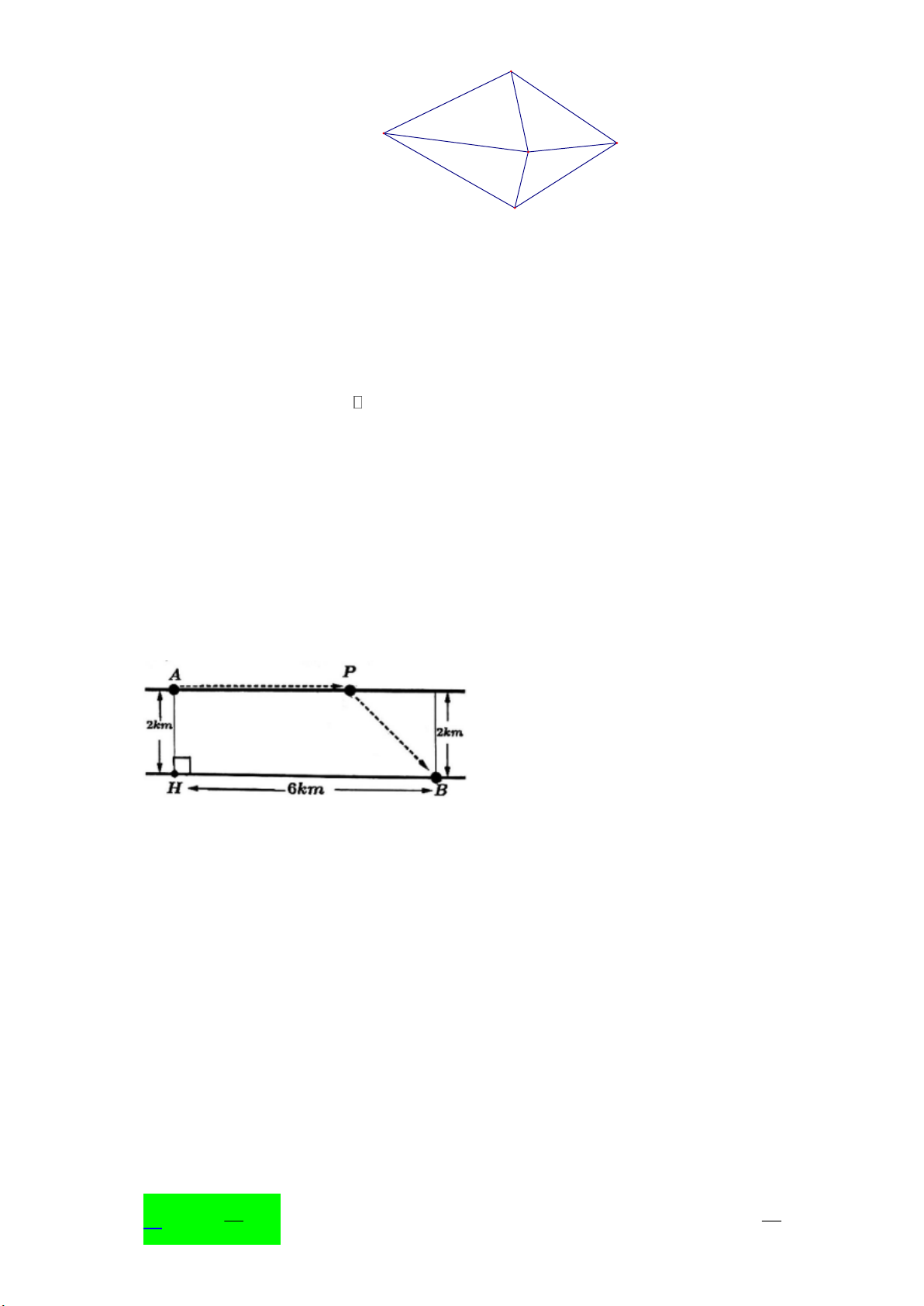
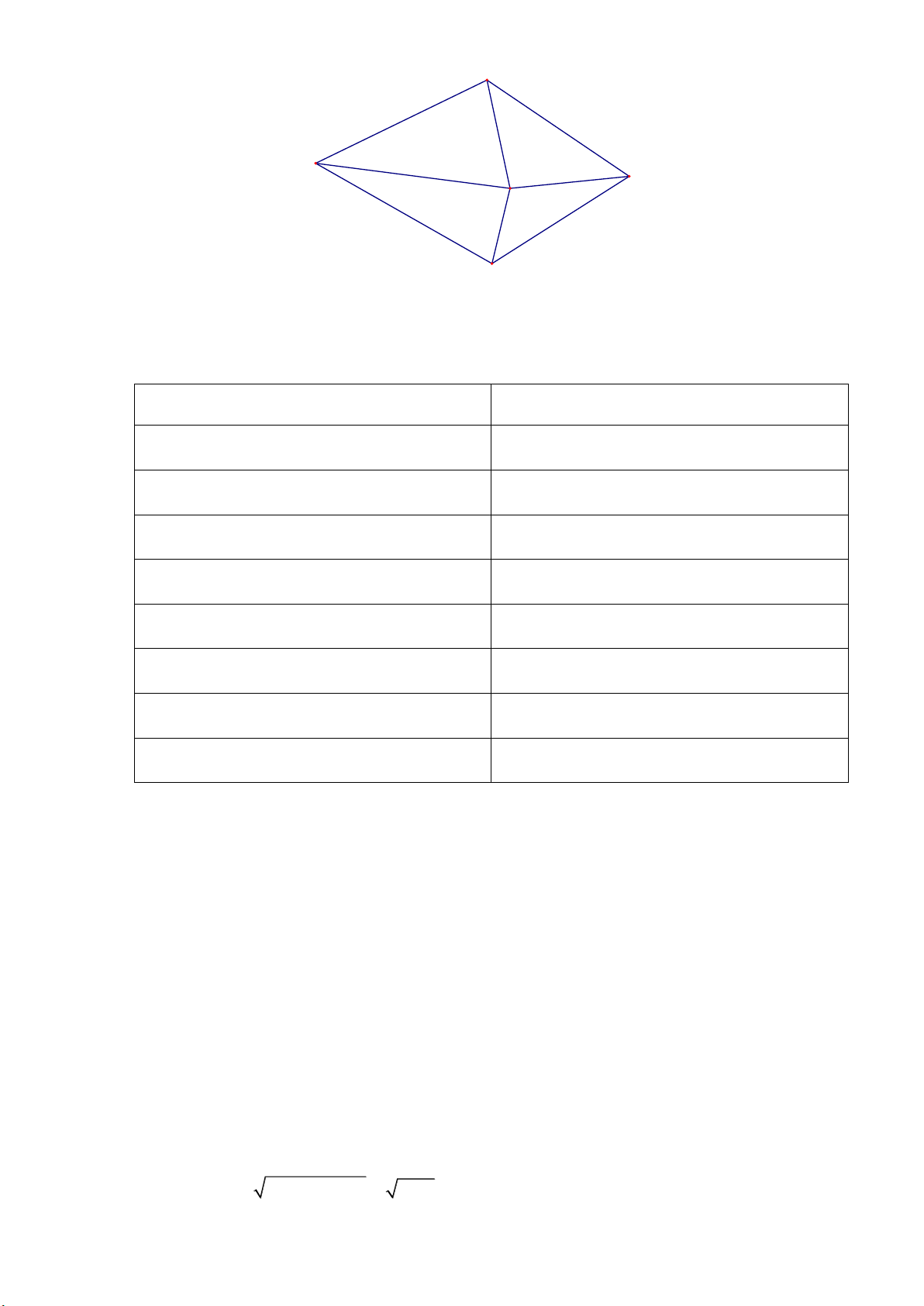
Câu 2. Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hinh vẽ bên durớt). Chi phí di
chuyển giữa các thảnh phố được mô tả trên hình (đơn vi tinh: triệu đồng). Xe giao hàng cưa công ty xuất
phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần sau đó
trở lại thành phố ban đầu. Tìm chi phí thấp nhất cùa xe giao hàng. Trang 3 B 9 14 8 A 10 12 E C 14 11 13 D
Câu 3. Một máy bay không người lái bay lên tại 1 điểm. Sau một thời gian bay, cách điểm xuất phát về phía Bắc
50km và về phía Tây 20km , đồng thời cách mặt đất 1km . Lúc đó máy bay cách vị trí tại điểm
xuất phát của nó là a km , giá trị cùa a là bao nhiêu? ( kết quả làm tròn đến hàng phần mười). 2
Câu 4. Cho f x là hàm số liên tục trên
, biết f x 3 2
16x 15x  2x f
 ttd 21. Giá trị của f 2 1 bằng bao nhiêu?
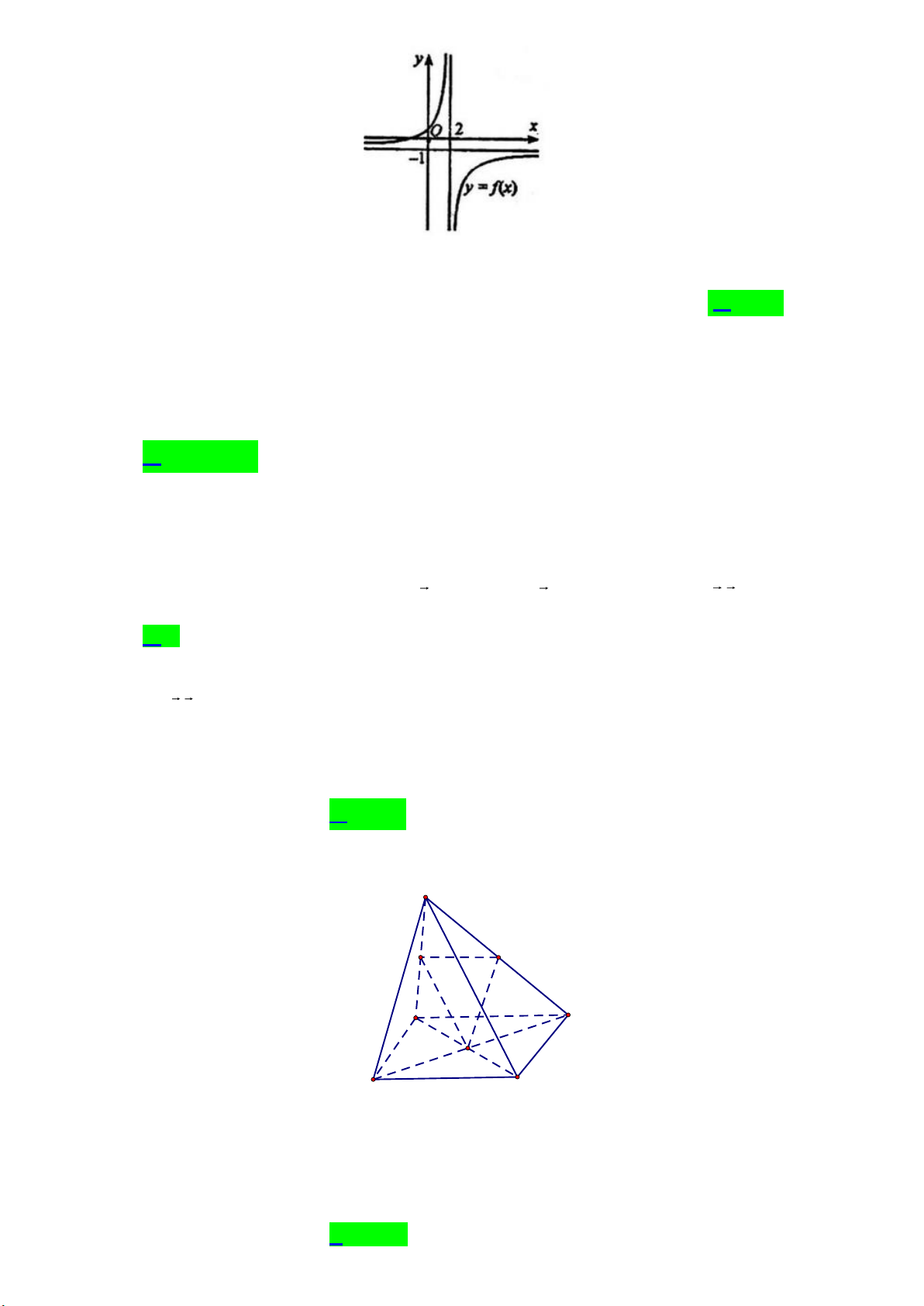
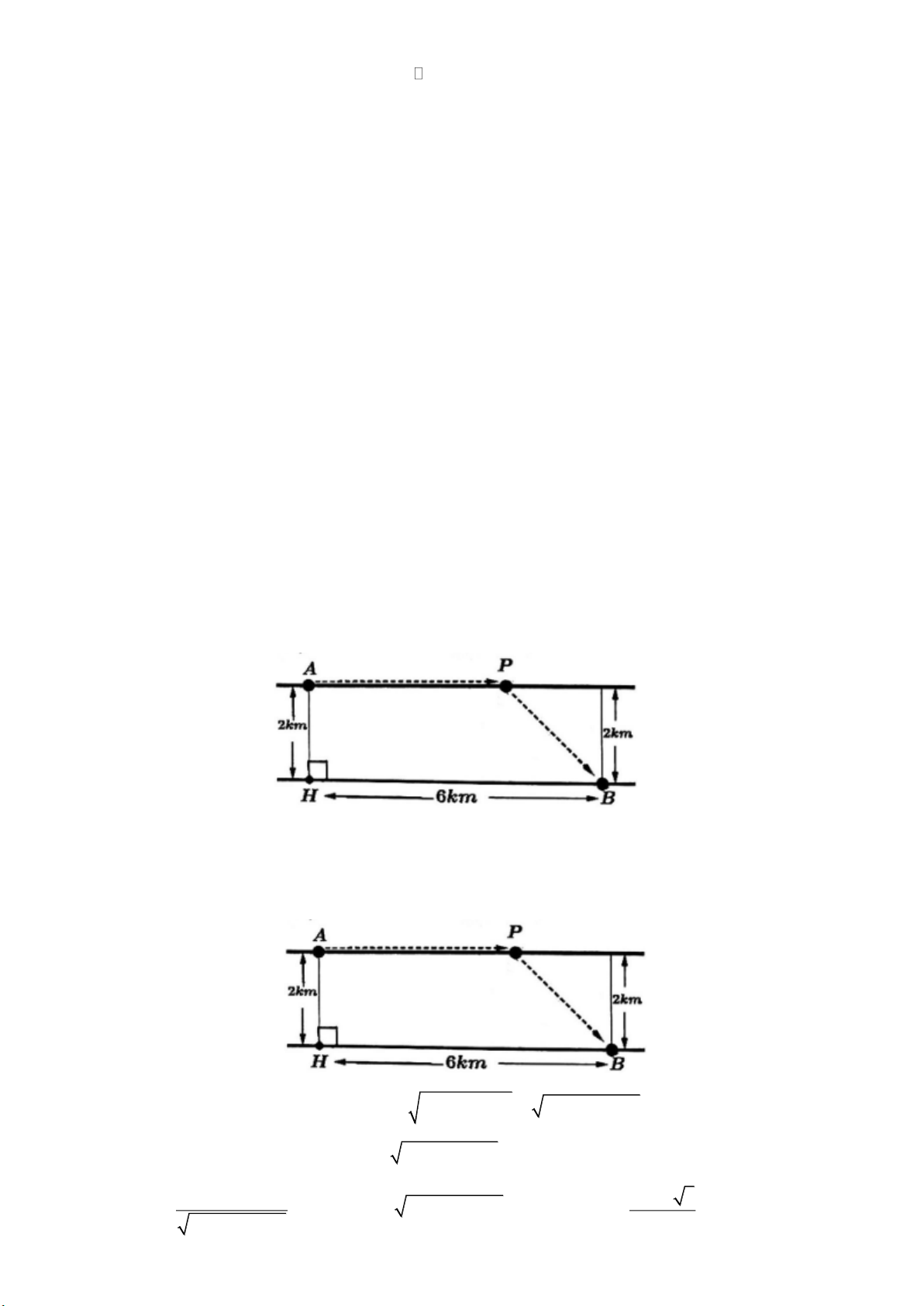
Câu 5. Người ta muốn lắp đặt một ống dẫn dầu từ nhà máy lọc dầu ở vị trí A đến kho chứa dầu đặt ở vị trí B qua
một con sông rộng 2km , dài 6km . Chi phí lắp đặt đường ống dẫn dầu trên mặt đất để nối từ nhà máy lọc
dầu đến trạm trung chuyển tại vị trí P là 4 tỷ VNĐ/ 1km và chi phí lắp đặt ống dẫn dầu dưới dòng sông để
nối từ P đến kho chứa dầu tại vị trí B là 8 tỷ VNĐ/1km (như hình vẽ dưới). Hỏi để chi phí lắp đặt ít nhất cần
đặt vị trí P cách nhà máy lọc dầu là bao nhiêu kilômét? (làm tròn kết quả đến hàng phần trăm)
Câu 6. Trong đợt củng hộ sách giáo khoa cho những học sinh bị ảnh hưởng do trận lũ lụt vừa qua, lớp 12A nhận
được 20 cuốn sách gồm 5 cuốn sách toán học, 7 cuốn sách Vật lí, 8 cuốn sách Hóa học, các sách cùng
môn học là giống nhau. Số sách này được chia đều cho 10 học sinh, mỗi học sinh chỉ được nhận đúng 2
cuốn sách khác môn học. Trong số 10 học sinh nhận sách đợt này có bạn Hưng và bạn Thành. Tính xác
suất để 2 cuốn sách mà bạn Hưng nhận đươc giống 2 cuốn sách của bạn Thành (làm tròn kết quả đến hàng phần trăm) HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Nguyên hàm của hàm số 5
f (x)  x là 6 x 4 x
A. F (x)   C. B. 6
F(x)  5x  . C C. 4
F(x)  5x  . C
D. F (x)   C. 6 4 Trang 4 Lời giải
Áp dụng công thức, ta có nguyên hàm của 5
f (x)  x là: 5 1  6 x x 5
F (x)  x dx   C   C  . 5 1 6 Vậy đáp án đúng là A. 9 5
Câu 2. Cho hàm số y f (x) liên tục trên . Biết
f (x)dx  25  thì f (x)dx  bằng 5 9 A. 9. B. 5. C. 25. D. 25.  Lời giải 9 5 Ta có:
f (x)dx  25 
f (x)dx  2  5.   5 9
Câu 3. Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là A. 4,84 . B. 2,10 . C. 2, 09 . D. 6,94 . Lời giải
Cỡ mẫu: n  3  8  7 12  7 11  39 . Q x 2 20 Q x  4;5 1 10   39  3 155 4 Q  4  .1   4,84375 . 1 8 32 Câu 4.
Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC có ba đỉnh A2;1;  3 , B4;2; 
1 , C 3;0;5. Tọa độ trọng tâm G của tam giác ABC là
A. G3;1;  1 . B. G 3;1;  1 . C. G 1;3;  1 . D. G 1  ;3;  1 . Lời giải
Trọng tâm G của tam giác ABC là G 3;1;  1 . ax b
Câu 5. Cho hàm số y
, c  0, ad bc  0 cx
có đồ thị như hình bên. d Trang 5
Tiệm cận đứng của đồ thị hàm số đã cho là A. y  1  . B. y  2 . C. x  1
 . D. x  2 . Lời giải
Dựa vào đồ thị ta có tiệm cận đứng của đồ thị hàm số là x  2 .
Câu 6. Tập nghiệm của bất phương trình log  x   1 1 là
A. 11;   . B.  ;  1 
1 . C. 11; . D. 1; . Lời giải Ta có x  1 log
1 1  x 110  x 11.
Câu 7. Trong không gian Oxyz , cho hai vectơ a  1; 2   ;1 và b  2; 4  ; 2  . Khi đó . a b bằng A. 8 B. 8  C. 12 D. 12  Lời giải Ta có . a b  1.2   2  . 4   1. 2    8 .
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M và N theo thứ tự là
trung điểm của cạnh SA và SD . Mặt phẳng nào sau đây song song với mặt phẳng MNO ? A. SABB. SBCC. SCDD. SADLời giải S M N A D O B C
Vì ABCD là hình bình hành nên O là trung điểm của AC và BD . Lại có M và N theo thứ tự là
trung điểm của SA và SD OM / /SC và ON / /SB  OMN  / / SBC . Câu 9.
Nghiệm của phương trình log x  3 là: 2 A. 2 x  3 . B. 3 x  2 . C. x  3. D. x  2 . Trang 6 Lời giải Ta có: 3
log x  3  x  2 . 2
Câu 10. Cho cấp số nhân u biết u .u  64 . Giá trị của u .u bằng: n  2 6 3 5 A. 8  . B. 64  . C. 64 . D. 8 . Lời giải
Gọi q là công bội của cấp số nhân u . Ta có 2 6
u .u u .q   2 u .q . 4 u .qu .u  64 2 6 1 1 1  n  3 5
Câu 11. Cho hình hộp ABC .
D EFGH (minh họa như hình bên). Vectơ nào sau đây bằng vectơ FH ? A B D C F E H G A. DB . B. BD . C. BA . D. AB . Lời giải
Nhận xét: Tứ giác BDHF là hình bình hành nên BD FH .
Câu 12. Cho hàm số có đồ thị như hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.   ;1  . B. 0; . C.  1  ;  1 . D. 0;  1 . Lời giải
Nhận xét: Trên khoảng 0; 
1 nhìn từ trái qua phải đồ thị đi lên nên hàm số đồng biến.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
f x  sin 2x x
Câu 1: [ NB-TH-TH-TH] Cho hàm số .          f  ; f           a) 2 2 2 2 . f ' x   b) Đạ cos 2x 1
o hàm của hàm số đã cho là . Trang 7        ;   
f  x  0   x x c) Phương trình
có hai nghiệm trên đoạn  2 2  là 6 và 6 .       ; 
y f x  
d) Giá trị nhỏ nhất của hàm số trên đoạn  2 2  là 2 . Lời giải Đáp án: Câu 1 a. Đúng b. Sai c. Đúng d. Đúng          f  ; f           a) 2 2 2 2 .            f  sin       ; f  sin              Ta có: 2 2 2 2 2 2 . Chọn Đúng
f  x   b) Đạ cos 2x 1
o hàm của hàm số đã cho là . 
f  x  sin 2x x  2 cos 2x 1 Ta có: . Chọn Sai.        ;   
f  x  0     x x c) Phương trình
có hai nghiệm trên đoạn 2 2 là 6 và 6 . Ta có:    f  x 1
 0  2cos 2x 1  0  cos 2x   cos  2x    k2  x    k k   2 3 3 6 .        x  ;        x x Do 2 2 nên 6 và 6 . Chọn Đúng.       ; 
y f x    
d) Giá trị nhỏ nhất của hàm số trên đoạn 2 2 là 2 . Trang 8    f  x 1
 0  2cos 2x 1  0  cos 2x   cos  2x    k2  x    k 2 3 3 6        x  ;   x   x  Do  2 2  nên 6 và 6 . Mà :      f  1,57    2  2     f    1,57    2  2     3  f     0,34    6  2 6    3  f    0,34     6 2 6       ; 
y f x  
Suy ra giá trị nhỏ nhất của hàm số trên đoạn  2 2  là 2 . Chọn Đúng
Câu 2. [ NB-TH-TH-VD] Một sợi dây kim loại dài 6cm . Người ta cắt sợi dây đó thành hai đoạn. Đoạn
có độ dài xcm được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông 0  x  6. x
a) Bán kính đường tròn là r   . 2  6  x
b) Diện tích hình vuông là   .  4     2 4
.x 12 x  36
c) Tổng diện tích hai hình là . 16 6 d) Khi x
thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất. 2   Lời giải
a) Sai b) Đúng c) Đúng d) Sai a) Đúng.
Do chu vi của đường tròn là x
x cm nên bán kính đường tròn là r  . 2 b) Đúng.
Chu vi của hình vuông là: 6  xcm0  x  6 
Độ dài một cạnh của hình vuông là: 6 x cm 4 2   
Diện tích hình vuông là: 6 x   .  4  Trang 9 c) Đúng.
Tổng diện tích của 2 hình là: 2 2 2 2  x   6  x x 36 12x x .   .      2  2   4  4 16 2 2
4x  36 12x   x
4  2x 12x 36   16 16 d) Đúng.    2 4
x 12x  36 Xét hàm số y  , 0  x  6 16 1 y 
. 2.4    x 12    16 12 6
y  0  x   2.4   4   BBT: 
Vậy tổng diện tích của hai hình bé nhất khi 6 x  4  
Câu 3. Hai bạn Bảo và Nam của lớp 12A cùng tham gia giải bóng bàn đơn nam do nhà trường tổ chức.
Hai bạn đó không cùng một bảng đấu vòng loại và mỗi bảng đấu vòng loại chỉ chọn một người
vào vòng chung kết. Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và bạn
Nam lần lượt là 0,8 và 0, 6 .
Gọi A là biến cố ” Có ít nhất một bạn lọt vào vòng chung kết”.
Gọi B là biến cố “ Chỉ có bạn Bảo lọt vào vòng chung kết”.
a) [NB] Xác suất để bạn Nam không lọt vào vòng chung kết là 0, 4 .
b) [TH] Xác suất để cả hai bạn lọt vào vòng chung kết là 0,8 .
c) [TH] Xác suất của biến cố A là 0, 48 .
d) [VD] Xác suất của biến cố B là 0, 32 . Lời giải
Đáp số: a) Đúng; b) Sai; c)Sai; d)Đúng.
a) [NB] Đúng vì: Xác suất để bạn Nam lọt vào vòng chung kết là 0, 6 .
Xác suất để bạn Nam không lọt vào vòng chung kết là 1 0,6  0, 4 .
b) [TH] Sai vì:
Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và Nam lần lượt là 0,8 và 0, 6 .
 Xác suất để cả hai bạn lọt vào vòng chung kết là 0,8.0,6  0, 48 . c) [TH] Sai vì: Trang 10
Ta có xác suất để cả hai bạn không lọt vào vòng chung kết là 1 0,8.1 0,6  0,08.
 Xác suất của biến cố A là 1 0,08  0,92 .
d) [VD] Đúng vì:
Xác suất để chỉ có bạn Bảo lọt vào vòng chung kết là 0,8.1 0,6  0,32
 Xác suất của biến cố B là 0,32 . Câu 4.
Cho hàm số y f x 3 2
x 3x  4 0;2
a) Hàm số y f x nghịch biến trên khoảng .
lim f x  
b) Giới hạn x . c) Gọi ,
A B lần lượt là hai điểm cực trị của hàm số. Khi đó độ dài AB bằng 5 . x 1
y f x d) Đồ thị hàm số
có đúng hai đường tiệm cận đứng. Lời giải a) Đúng, vì:
+ Tập xác định của hàm số y f x là: D  . + 2
y  3x  6x . x  0 + 2
y  0  3x  6x  0   . x  2 + Bảng xét dấu: 0;2
+ Vậy hàm số y f xnghịch biến trên khoảng . b) Đúng, vì:  
lim f x  lim  3 4 3 2
x  3x  4 3  lim x  1      3 x x x   + x x . c) Sai, vì:
+ Tọa độ điểm cực trị: A0;4, B2;0 + AB  2 5 . d) Sai, vì: x 1 x 1 y   f x 3 2 x  3x  4 + Xét hàm số . D  \  1  ;  2 + Tập xác định: . + Trường hợp 1: Trang 11 x 1 x 1 x 1 1 1 lim  lim  lim  lim  3 2
x x  3x  4
x  x   1  2
x  4x  4 x  x   1  2 1 1 1
x  4x  4 2 x 1
x  4x  4 9 .
Nên trường hợp này, đồ thị của hàm số không có tiệm cận đứng. + Trường hợp 2: x 1 x 1 lim   ;  lim    3 2  3 2 x2   x2 x 3x 4 x  3x  4
Nên trường hợp này, đồ thị của hàm số nhận x  2 làm tiệm cận đứng.
PHẦN III. Thí sinh trả lời từ câu 19 đến câu 22 Câu 1:
Cho hình chóp tứ giác đều S.ABCD , có cạnh đáy bằng 2, cạnh bên bằng 2 2 .
Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười) Lời giải Đáp án: 1,8 z S 2 2 y A D 2 O B C x
Chọn hệ trục tọa độ như hình vẽ, ta có
A 2;0;0; B0; 2;0, D0; 2;0, S 0;0; 6  .
Đường thẳng AB qua A và có vecto chỉ phương AB   2; 2;0
Đường thẳng SD qua D và có vecto chỉ phương SD  0; 2; 6
AD   2; 2;0. A , B SD    2 3;2 3;2.
AD   AB SD     6 6 d AB SD ; 2 6 2 6 0 4 2 ;     1,8 . A ; B SD 12 12  4 2 7 7   Câu 2:
Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hinh vẽ bên durớt). Chi phí di
chuyển giữa các thảnh phố được mô tả trên hình (đơn vi tinh: triệu đồng). Xe giao hàng cưa công ty
xuất phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần
sau đó trở lại thành phố ban đầu. Tìm chi phí thấp nhất cùa xe giao hàng. Trang 12 B 9 14 8 A 10 12 E C 14 11 13 D Lời giải Đáp án: 53 Đường đi Tống số chi phí
A B C E D A
9 14 12 14 11  60
A B E C D A
9 8 12 1311  53
A E B C D A
10 8 14 1311  56
A E D C B A
10 14 1314  9  60
A D C E B A
111312 8  9  53
A D E C B A
1114 12 14  9  60
A B C D E A
9 14 1314 10  60
A D C B E A
111314 8 10  56
Vậy chi phí nhỏ nhất của xe giao hàng là 53.
Câu 3. Một máy bay không người lái bay lên tại 1 điểm. Sau một thời gian bay, cách điểm xuất phát về
phía Bắc 50km và về phía Tây 20km , đồng thời cách mặt đất 1km . Lúc đó máy bay cách
vị trí tại điểm xuất phát của nó là a km , giá trị cùa a là bao nhiêu? ( kết quả làm tròn đến
hàng phần mười). Lời giải
Đáp án: 53,9 .
Chọn hệ trục toạ độ sao cho vị trí ban đầu của máy bay là O0;0;0 , vị trí cần tính là A20;50; 
1 . Khi đó độ dài AB là khoảng cách của máy bay đến điểm xuất phát. Nên 2 2 2 AB a  20  50 1  2901  53,9 Trang 13 2
Câu 4. Cho f x là hàm số liên tục trên
, biết f x 3 2
16x 15x  2x f
 ttd 21. Giá trị của 1
f 2 bằng bao nhiêu? Lời giải Đáp án: 39. 2 Giả sử f
 ttd  a và f x 3 2
16x 15x  2ax  21. 1 Khi đó ta có:
2 16t 15t 2at 2  2 2 3 2 1 t
d  a  2at t d   3 2
16t 15t  2  1 t
d  3a  4  a a  2     . 1 1 1
Do đó: f x 3 2
16x 15x  4x  21 nên f 2  39. Câu 5.
Người ta muốn lắp đặt một ống dẫn dầu từ nhà máy lọc dầu ở vị trí A đến kho chứa dầu đặt ở vị
trí B qua một con sông rộng 2km , dài 6km . Chi phí lắp đặt đường ống dẫn dầu trên mặt đất để
nối từ nhà máy lọc dầu đến trạm trung chuyển tại vị trí P là 4 tỷ VNĐ/ 1km và chi phí lắp đặt
ống dẫn dầu dưới dòng sông để nối từ P đến kho chứa dầu tại vị trí B là 8 tỷ VNĐ/1km (như
hình vẽ dưới ). Hỏi để chi phí lắp đặt ít nhất cần đặt vị trí P cách nhà máy lọc dầu là bao nhiêu
kilômét? (làm tròn kết quả đến hàng phần trăm) Lời giải
Đáp số: 4,85
Đặt AP xkm,0  x  6 .Khi đó PB    x2 2 2 6
 2  x 12x  40
Chi chí lắp đặt ống dẫn là: C x 2
 4x 8 x 12x  40 (tỷ)   C x 4 2x 12  4  , C x 18 2 3 2
 0  x 12x  40 12  2x x  0;6 2   3 x 12x 40 Trang 14    C    C   18 2 3 0 16 10, 6  40, C    24  8 3   3      C x 18 2 3 min  C    24  8 3    0;6 3   18  2 3
Vậy chi phí lắp đặt ít nhất khi đặt vị trí P cách nhà máy lọc dầu  4,85km 3
Câu 6. Trong đợt củng hộ sách giáo khoa cho những học sinh bị ảnh hưởng do trận lũ lụt vừa qua, lớp
12A nhận được 20 cuốn sách gồm 5 cuốn sách toán học, 7 cuốn sách Vật lí, 8 cuốn sách Hóa
học, các sách cùng môn học là giống nhau. Số sách này được chia đều cho 10 học sinh, mỗi học
sinh chỉ được nhận đúng 2 cuốn sách khác môn học. Trong số 10 học sinh nhận sách đợt này
có bạn Hưng và bạn Thành. Tính xác suất để 2 cuốn sách mà bạn Hưng nhận đươc giống 2
cuốn sách của bạn Thành (làm tròn kết quả đến hàng phần trăm) Lời giải
Đáp số: 0,31 Cách 1
Gọi x là số học sinh nhận sách Toán và Lí
y là số học sinh nhận sách Lí và Hóa
z là số học sinh nhận sách Hóa và Toán x y  7 x  2  
Theo bài ra ta có hệ;  y z  8  y  5   z x  5 z  3  
Ta chia 20 cuốn sách thành 10 bộ trong đó có 2 bộ sách Toán và Lí, 5 bộ sách Lí và Hóa, 3 bộ Toán và Hóa được trao.
Bạn Thành và Hưng nhận 2 bộ sách trong số 10 bộ được trao
+) Số phần tử của không gian mẫu: n 2  C  45 10
+) Gọi A là biến cố; “Hưng nhận 2 cuốn sách giống bạn Thành”
TH1: Thành và Hưng nhận sách Toán và Lí có 2 C cách 2
TH2: Thành và Hưng nhận sách Hóa và Lí có 2 C cách 5
TH3: Thành và Hưng nhận sách Toán và Hóa có 2 C cách 3  n  2 2 2
A C C C  14 2 5 3
+) Xác suất của biến cố A là: P A 14   0,31 45 Cách 2:
Gọi x là số học sinh nhận sách Toán và Lí
y là số học sinh nhận sách Lí và Hóa
z là số học sinh nhận sách Hóa và Toán Trang 15x y  7 x  2  
Theo bài ra ta có hệ;  y z  8  y  5   z x  5 z  3  
+) Số phần tử của không gian mẫu : n 5 3 2
C .C .C  2520 10 5 2
+) Gọi A là biến cố: “Hưng nhận 2 cuốn sách giống bạn Thành”
TH1: Thành và Hưng nhận sách Toán và Lí có 5 3
1.C .C  56 cách 8 3
TH2: Thành và Hưng nhận sách Hóa và Lí có 3 3 2
1.C .C .C  560 cách 8 5 2
TH3: Thành và Hưng nhận sách Toán và Hóa có 1 5 2
1.C .C .C  168 cách 8 7 2  n 
A  56  560 168  784
+) Xác suất của biến cố A là: P A 784   0,31 2520 Trang 16

Tài liệu liên quan: