

Preview text:
TRƯỜNG THCS NGA THIỆN ĐỀ THI THỬ VÀO LỚP 10 Năm ho ̣c: 2017 – 2018 MÔN: TOÁN
Thời gian làm bài: 120 phút Câu 1 (2,0 điểm )
1. a) Giải phương trình: 4x + 3 = 0 3
x y 7
b) Giải hệ phương trình:
2x y 3
2. Rút gọn biểu thức sau: b 1 1 b 1 A =
Víi b 0;b 1 b 1
b 1 b 2
Câu 2 (2.0 điểm) : Cho phương trình: x2 – 2(n+2)x + n2 + 4n +3 = 0.
a) Giải phương trình khi n = 0
b) Chứng minh rằng : Phương trình trên luôn có hai nghiệm phân biệt x1, x2 với mọi giá trị của n.
c) Tìm giá trị của n để biểu thức A = 2 2
x x đạt giá trị nhỏ nhất. 1 2
Câu 3 (2,0 điểm ) : Trong mặt phẳng toạ độ Oxy, cho Parabol (P) : y = x2 và đường thẳng (d) : y = 2x + 3
1. Chứng minh rằng (d) và (P) có hai điểm chung phân biệt . Tìm tọa độ giao điểm.
2. Gọi M và N là các điểm chung của (d) và (P) . Tính diện tích tam giác OMN ( O là gốc toạ độ) Câu IV (3,0 điểm)
Cho đường tròn tâm O đường kính MN. Trên đường tròn lấy điểm C sao cho
MC < NC (C M). Các tiếp tuyến tại N và C của (O) cắt nhau ở điểm D, MD cắt (O) tại E (E M) . 1) Chứng minh NE2 = ME.DE.
2) Qua C kẻ đường thẳng song song với ND cắt MN tại H, DO cắt NC tại F.
Chứng minh tứ giác CHOF nội tiếp .
3) Gọi I là giao điểm của MD và CH. Chứng minh I là trung điểm của CH.
Câu V ( 1,0 điểm) Cho x, y, z là các số thực dương. 3 3 3
3(x y z ) 1 Chứng minh rằng 3 P . 2
4(xy yz zx) (x y z) 4 Hết
Họ và tên thí sinh: ………………………………………………. Sô báo danh:……………
HƯỚNG DẪN CHẤM ĐỀ B CÂU NỘI DUNG ĐIỂM 3 1.a) x= 0,5 4
b) Giải hệ phương trình 3
x y 7 5 x 10 x 2
2x y 3
2x y 3 y 1 x 2
Vậy hệ phương trình đã cho có nghiệm y 1 0,5 1 2. Rót gän biÓu thøc:
(2điểm) Víi a 0;a 1 ta cã: b 1 1 b 1
b 1 b 1 1 b 1 A = = b 1
b 1 b 2 b 1
b 1 b 2 1.0 b 2 1 1 b b b 2 1 b 1 = b b 1 b 2 b 1 b 2
VËy A = b Víi b 0;b 1
a) Xét phương trình: x2 – 2(n+2)x + n2 + 4n +3 = 0. 0,75
Thay n = 0 vào giải được x = 1; x = 3
b) Chứng minh rằng : Phương trình trên luôn có hai nghiệm phân biệt
x1, x2 với mọi giá trị của n. 2
Ta có 2 (n 2) n 4n 3 1> 0 với mọi n. 0,75
Vậy phương trình đã cho luôn có hai nghiệm phân biệt x1, x2 với mọi giá trị của n.
c) phương trình đã cho luôn có hai nghiệm phân biệt x1, x2 với mọi 2 x x 2(n 2) 1 2 (điểm)
giá trị của n. Theo hệ thức Vi-ét ta có : x .x 2 n 4n 3 1 2 A = 2 2 x x = (x 1 2
1 + x2)2 – 2 x1x2 = 4(n + 2)2 – 2(n2 + 4n +3) = 2n2 + 8n+ 10 0,5 = 2(n2 + 4n+4) + 2
= 2(n + 2)2 + 2 ≥ 2 với mọi n.
Suy ra minA = 2 n + 2 = 0 n = - 2
Vậy với n = - 2 thì A đạt min = 2
1. Chứng minh rằng (d) và (P) có hai điểm chung phân biệt 3
Hoành độ giao điểm đường thẳng (d) và Parabol (P) là nghiệm của phương trình
x2 = 2x + 3 => x2 – 2x – 3 = 0 có a – b + c = 0
Nên phương trình có hai nghiệm phân biệt c 3 0,5 x1 = -1 và x 3 2 a 1 Với x
1 = -1 => y1 = (-1)2 = 1 => M (-1; 1) Với x 0,5
2 = 3 => y2 = 32 = 9 => N (3; 9)
Vậy (d) và (P) có hai điểm chung phân biệt M và N
2. Gọi M và N là các điểm chung của (d) và (P) . Tính diện tích tam giác
OMN ( O là gốc toạ độ) y
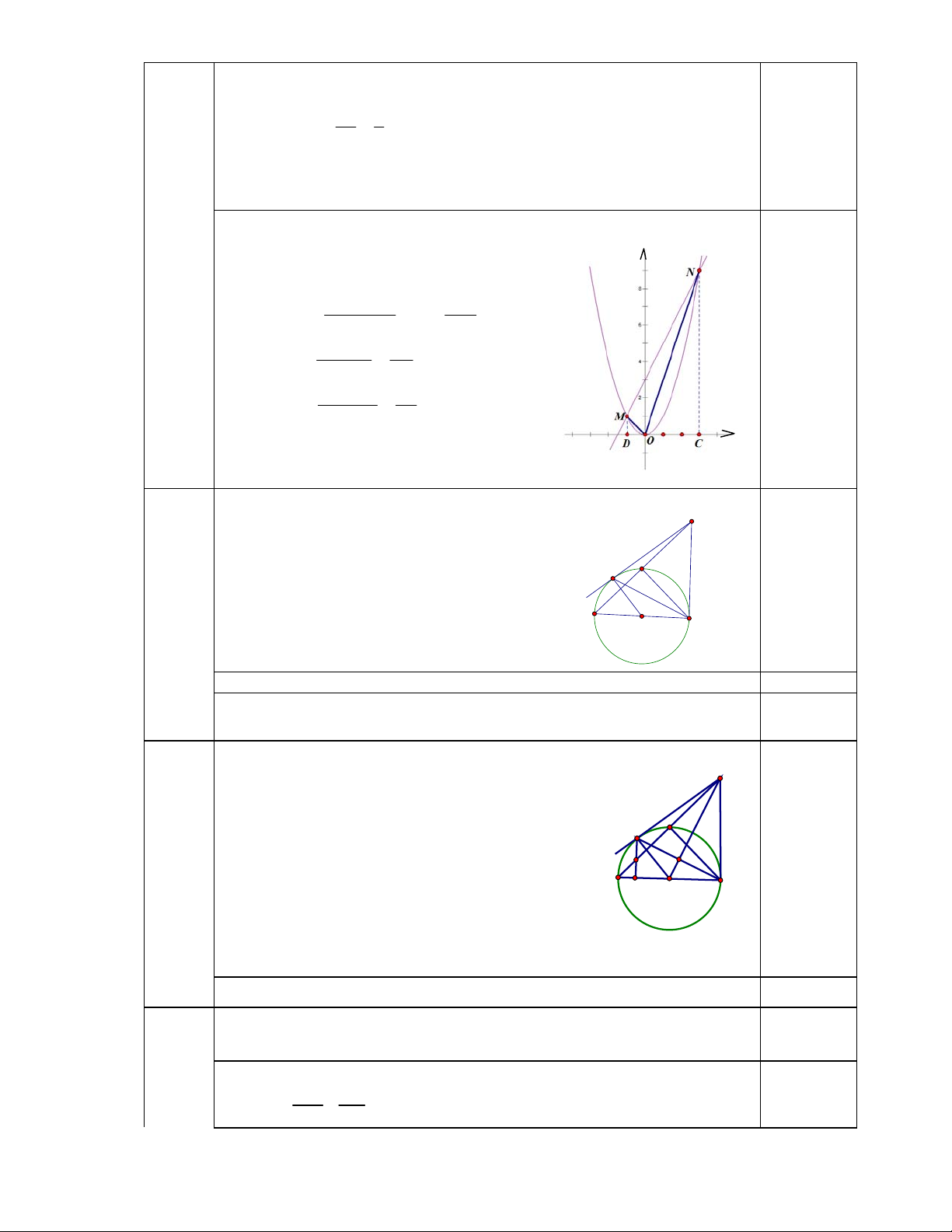
Ta biểu diễn các điểm M và N trên mặt phẳng toạ độ Oxy như hình vẽ MD NC 1 9 S .DC .4 20 MNCD 2 2 NC.CO 9.3 0,5 S 13,5 NOC 2 2 . MD DO 1.1 S 0,5 MOD 2 2
Theo công thức cộng diện tích ta có: x
S(MBC) = S(MNCD) - S(NCO) - S(MDO) 0,5
= 20 – 13,5 – 0,5 = 6 (đvdt) Câu 4 (3điểm D ) C E M N O
1 (1đ ) Vì ND là tiếp tuyến của (O) nên ND ON 0,25 Suy ra: ΔMND vuông tại N
Vì MN là đường kính của (O) nên ME NE 0,25
Áp dụng hệ thức lượng trong ΔMND ( 0 MND=90 ;NE MD) 0, 5 Ta có NE2 = ME.DE ( đpcm) D
Ta có: + DC = DN ( tính chất tiếp tuyến cắt nhau)
+ OC = ON (Bán kính đường tròn (O) ) C E
Suy ra DO là trung trực của CN 0,25 2(1 đ) Suy ra DO NC 0 CFO 90 (1) I F M N Lại có CH // ND (gt), H O 0,25
mà MN ND (vì ND là tiếp tuyến của (O)) => CH MN => 0 OHC 90 (2) 0,25
Từ (1) và (2) ta có 0
OFC OHC 180 => tứ giác CHOF nội tiếp 0,25 Có CH //ND=>
HCN CND (hai góc ở vị trí so le trong) mà 0,25 ΔNCD cân tại D =>
CND DCN nên CN là tia phân giác của HCD
3( 1đ) do CM CN => CM là tia phân giác góc ngoài đỉnh C của 0,25 MI CI ΔICD = (3) MD CD MI HI 0,25
Trong ΔMND có HI // ND => = (4) MD ND CI HI 0,25 Từ (3) và (4) => =
mà CD=ND CI=HI I là trung điểm của CD ND CH Ta có 3 3 3 3
(x y z) (x y z ) 3(x y)( y z)(z x) 0,25
Áp dụng BĐT Cauchy cho 3 số không âm x+y; y+z; z+x ta có: 0,25 3
(2x 2y 2z) 8
(x y)( y z)(z x)
x y z3 27 27 1
x y z x y z3 3 3 3 9 2
(x y z) 0,25 Lại có 2 2 2
x y z xy yz zx xy yz zx 3 3
(x y z) 3 3 3 3
3(x y z ) 1 1 Do đó 9 P Câu 5 2
4(xy yz zx) (x y z) 4 2 2
(x y z)
(x y z) (1đ) 3
x y z 1
x y z
x y z 1 2 2 4
(x y z) 8 8
(x y z)
x y z x y z 1 3 33 . . 2 8 8
(x y z) 4 0,25
x y z 2
Dấu bằng xảy ra khi x y y z z x
x y z 3
x y z 1 2 8
(x y z) 3 2
Vậy P Khi x y z . 4 3




