Đề thi thử tuyển sinh vào lớp 10 năm 2020-2021 môn toán chuyên- Đề 1 (có lời giải)

ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2020 – 2021
Môn thi: TOÁN CHUYÊN
Thời gian làm bài: 120 phút
Câu 1. (2,0 điểm) Chứng minh rằng hàm số y   2
m  2m 10x  2021luôn nghịch
biến với mọi giá trị của tham số m
Câu 2. (2,0 điểm) Giải phương trình : 2
4  x  6  2 2  x  3 2  x
Câu 3. (2,5 điểm) Tìm các số tự nhiên n sao cho 2
n 18n  2020 là số chính phương
Câu 4. (2,5 điểm) Cho hình thang ABCD AB / /CD , hai đường chéo vuông góc với
nhau. Biết AC  8c , m BD  6c .
m Tính chiều cao của hình thang
Câu 5. (1,5 điểm) Chứng minh rằng với mọi số thực , a , b ,
c d,eta luôn có: 2 2 2 2 2
a  b  c  d  e  ab  c  d  e
Câu 6. (1,5 điểm) Cho phương trình: 2
x  mx  n  0, trong đó x là ẩn số, , m n là tham
số thỏa mãn m  n  4. Tìm các giá trị của ,
m n để phương trình có hai nghiệm phân
biệt x , x sao cho 2
x  x  x 1 2 1 2 2
Câu 7. (2,0 điểm) Một tổ chức từ thiện cần chia đều một số quyển vở thành các phần
quà để tặng cho các cháu nhỏ ở một trung tâm nuôi dạy trẻ mồ côi. Nếu phần quà
giamr 6 quyển vở thì sẽ có thêm 5 phần quà nữa cho các cháu, còn nếu mỗi phần quà
giảm đi 10 quyển vở thì các cháu sẽ có thêm 10 phần quà. Hỏi tổ chức từ thiện trên có bao nhiêu quyển vở ?
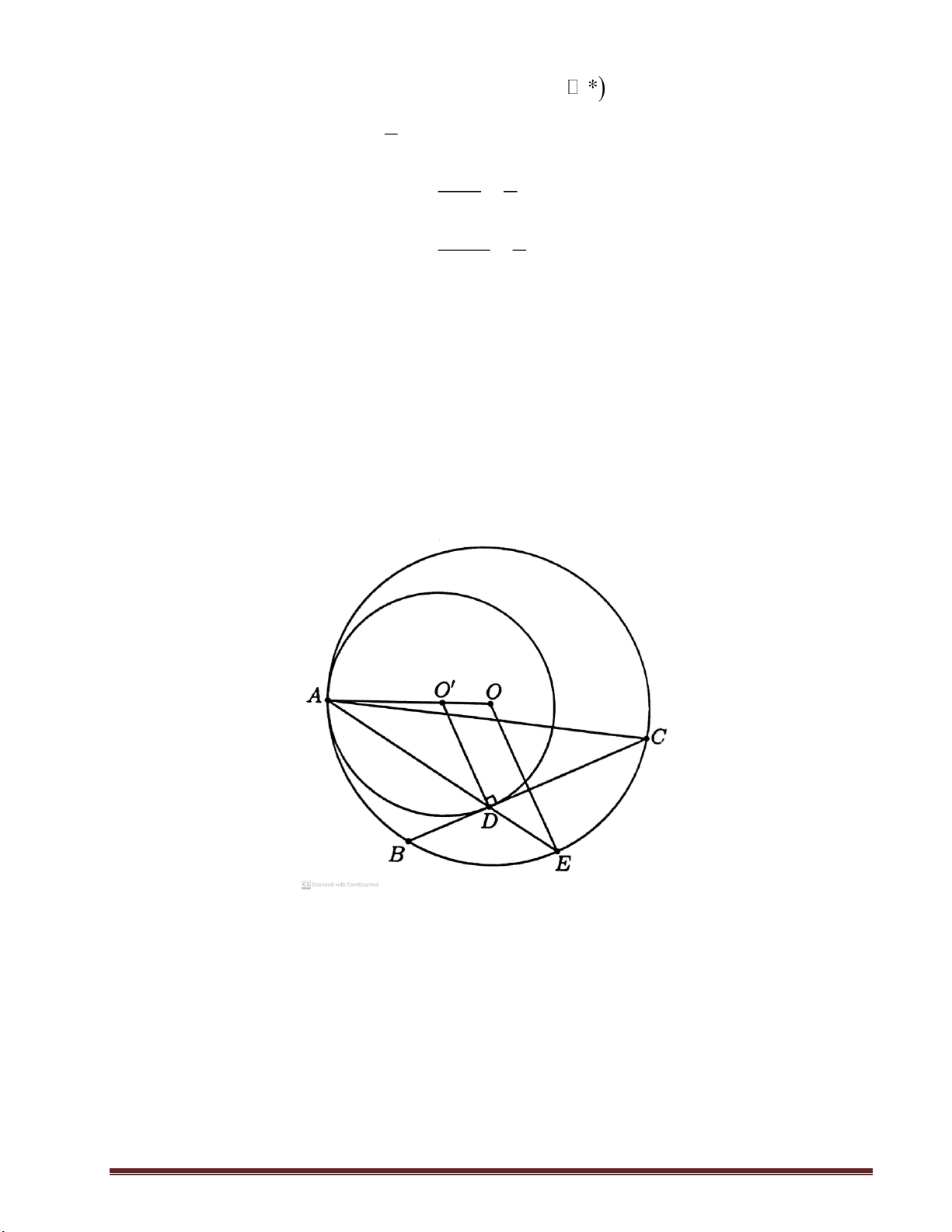
Câu 8. (2,5 điểm) Cho hai đường tròn  ;
O R và đường tròn O; R ' tiếp xúc trong tại
điểm AR  R'.Gọi BC là một dây của đường tròn lớn tiếp xúc với đường tròn nhỏ
tại D. Chứng minh rằng AD là tia phân giác của BAC
Câu 9. (1,5 điểm) Cho các số thực ,
x y, z đôi một khác nhau thỏa mãn 3 x  3x 1; 3 3
y  3y 1; z  3z 1.Tính giá trị biểu thức 2 2 2
S  x  y  z
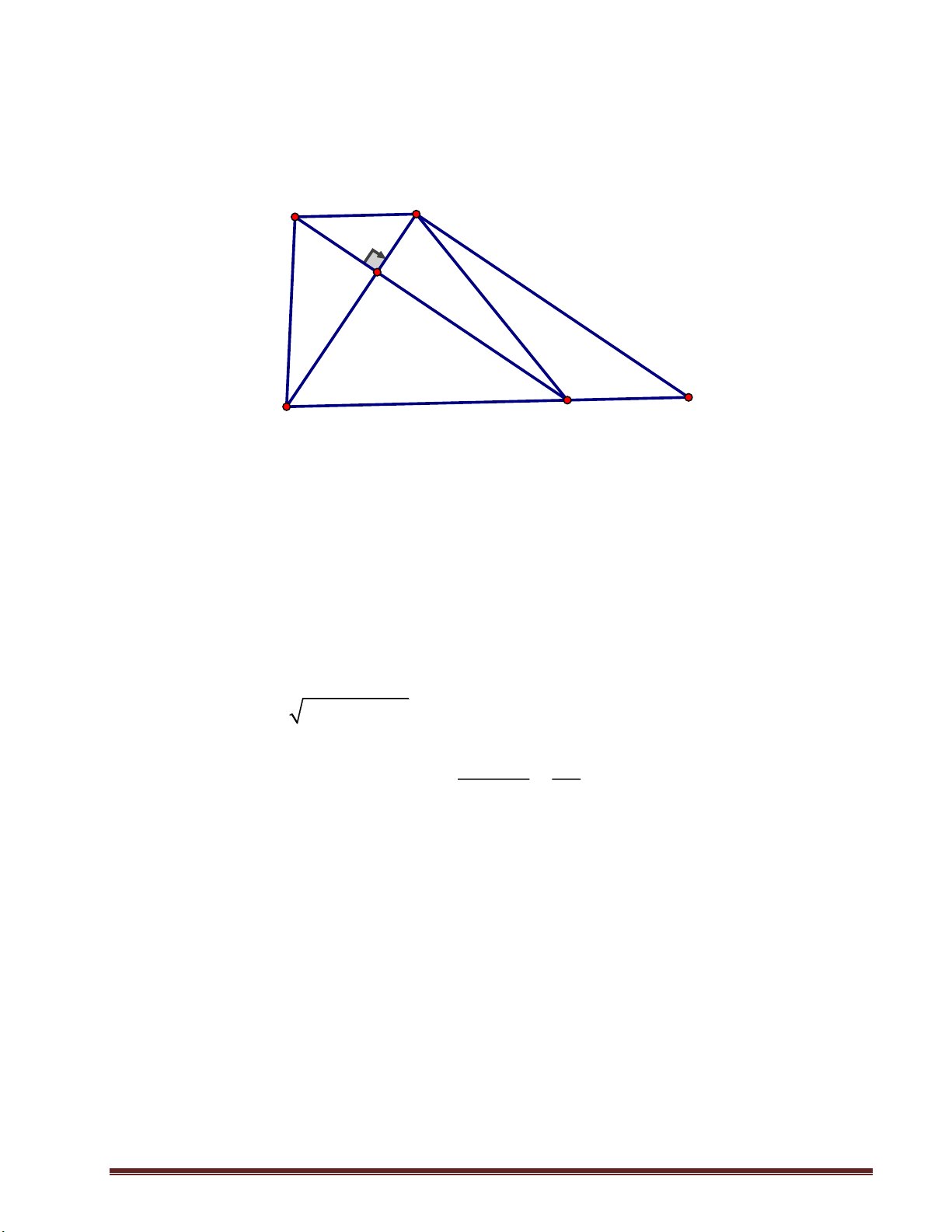
Câu 10. (2,0 diểm) Cho tam giác nhọn ABC.Gọi AH, B ,
D CK là các đường cao của
tam giác  H  BC, D  AC, K  AB.Chứng minh rằng: S HDK 2 2 2
 cos A  cos B  cos C 1 SABC Trang 1 ĐÁP ÁN Câu 1. 2 Ta có: 2 m  m    2 m  m     2 2 10 2 10
m  2m  10  m   1  9  0 m  
Nên hàm số đã cho luôn nghịch biến với mọi giá trị của tham số m Câu 2. ĐKXĐ: 2   x  2
PT  2  x2  x  6  2 2  x  3 2  x
  2  x  3 2  x  2  0  2  x  3 x  7(ktm)        x  2(  tm) 2 x 2 Vậy x  2  Câu 3. Đặt 2 2
n 18n  2020  a a   *  n  2   a 
 a  n  2 2 2 9 1939 1939 9
 a  n  9a  n  9 1.1939  7.277
a  n  9 1 a  970   (tm)
a  n  9 1939 n  960
Do a  n  9  a  n  9   a n 9 7     a 142   (tm)
a  n  9  277 n 126
Vậy n  126 hoặc  960 Trang 2 Câu 4. A B E M C D
Giả sử DB và AC cắt nhau tại E. Kẻ đường thẳng BM / / AC, M CD
Gọi h cm là độ dài chiều cao của hình thang
Xét tứ giác ABMC có AB / /CM , AC / /BM  ABMC là hình bình hành
 AB  CM và AC  BM  8cm
Vì BD  AC, BM / / AC  BM  B .
D Áp dụng định lý Pytago trong tam giác vuông BDM , ta có: 2 2 DM 
BD  BM  10(cm) B . D BM 6.8 Ta có: 2S  B . D BM  . h DM  h    4,8(cm) DBM DM 10
Vậy chiều cao của hình thang là 4,8cm Trang 3 Câu 5. 2 2 2 2 2
a  b  c  d  e  a b  c  d  e 2 2 2 2 2
 4a  4b  4c  4d  4e  4ab  c  d  e   2 2
a  4ab  4b    2 2
a  4ac  4c    2 2
a  4ad  4d    2 2
a  4ae  4e   0
 a  2b2  a  2c2  a  2d 2  a  2e2  0(luondung)  dfcm Câu 6.
Phương trình có hai nghiệm phân biệt m    2 2
   m  n  m    m 2 4 4. 4
 m  4m 16  2 2 5 0  
m  2  2 5
Vì x , x là nghiệm của phương trình đã cho nên 2
x  mx  n  0 1 2 2 2 2
 x  mx  n  mx  4  m 2 2 2  m   x  1  2 Vì 2
x  x  x  0  x  x   1 2 2 1 2  m   x  2  2 Khi đó ta có: 2
x  x  x  x  mx  4  m 1 2 2 2 2 m   m    
.1 m  4  m 2 2
 m    m   1 m  8 2m 2
 m    m    m  m   8  2m
  2  m 2
 m  2m  8  m  2m  4 m  2(ktm)   m  4  0   m  4 
  m  4         m  4  2 2 2 2
 m  4m 16
m  8m 16  m  4m 16 m  4 
 m8(ktm)
Vậy không có giá trị m thỏa mãn đề bài. Câu 7.
Gọi số quyển vở tổ chức đó có là a (quyển) a  * Trang 4
Gọi số vở ở mỗi phần quà ban đầu là b (quyển) b  * Khi đó số a
phần quà ban đầu là (phần quà) b  a a   5   Theo đề b 6 b
bài ta có hệ phương trình :  a a   10 b 10 b ab  a 
b  6  5bb  6 2
6a  5b  30b     ab  a 
b 10 10bb 10 2
a  b 10b
b  0(ktm) 2 b   30b  0  a  600(tm)  
 b  30(tm)   2
a  b 10b b    30 2
a  b 10b
Vậy tổ chức từ thiện đó có 600quyển vở Câu 8.
Giả sử AD cắt  ;
O R tại điểm thứ hai là E Vì O
 ' ADcân tại O doO' A  O'D  O' AD  O'DA Vì O
 AE cân tại OdoOA  OE  OAE  OEA
Suy ra O' DA  OE ,
A hai góc này ở vị trí đồng vị  O' D / /OE
Mà O' D  BC nên OE  BC Trang 5 Xét  ;
O R có OE  BC  E là điểm chính giữa của cung BC
 cung BE cung CE  B
 AE  EAC (góc nội tiếp chắn hai cung bằng nhau)
 AE là phân giác của BAC  Câu 9. Vì ,
x y, z đôi một khác nhau và thỏa mãn đề bài nên ,
x y, z là ba nghiệm phân biệt của phương trình 3
A  3A  1  0 và  A  x A  y A  z   0 3 2
 A  A x  y  z  Axy  yz  zx  xyz  0
x  y  z  0 
 xy  yz  zx  3  xyz  1  
 S  x  y  z  x  y  z2 2 2 2
 2xy  yz  zx 2  0  2.3  6 Câu 10.
Xét tứ giác BKEH có 0 0
BKE  BHE  90  BKE  BHE  180  BKEH là tứ giác nội tiếp  B  HK  B
 EK (cùng chắn cung BK)
Chứng minh tương tự , tứ giác AKED nội tiếp  KAD  BEK (cùng bù góc KED)
Chứng minh tương tự , tứ giác HEDC nội tiếp  C  HD  C
 ED (chắn cung CD) Mà C  ED  B
 EK (đối đỉnh) K  AD  B  EK  B  HK  C  HD  B  AC 0 0 0  K
 HD 180  B  HK  C
 HD 180  2. B
 AC 180  2. A 
Áp dụng công thức sin ta có: HK HD  0 . .sin 180  2 A S   HK.H . D sin 2A 2HK.H . D cos A HDK    S A . B AC.sin A A . B AC.sin A A . B AC ABC Xét B  KH và B  CAcó: ABC  chung; 0
BKH  BEH  180  HED  B  CA HK BK BH  BKH   ( BCA g.g)    AC BC AB Trang 6 Tương tự HD CH CD , C  HD C  AB    AB CA CB AD AK BK BH CH CD Mà cos A   ;cos B   ,cosC   AB AC BC BA CA CB S 2HK.H . D cos A BK CD HDK   2. . .cos A  2cos .
B cosC.cos A S A . B AC BC BC ABC  2cos .
B cosC.cos  B  C   2
 cos BcosC cosB  C Thay vào ta có: SHDK 2 2 2  A  B  C   B C B  C 2  B  C 2 2 cos cos cos 2cos .cos .cos cos
 cos B  cos C SABC  2
 cos BcosC cos .
B cos C  sin .
B sin C   cos .
B cos C  sin . B sin C 2 2 2
 cos B  cos C  cos . B cosC  sin .
B sin C cos .
B cos C  sin .
B sin C  2cos . B cos C  2 2
 cos B  cos C  cos . B cosC  sin .
B sin C cos .
B cos C  sin Bsin C  2 2
 cos B  cos C 2 2 2 2  cos . B cos C  sin . B sin 2 2
C  cos B  cos C 2 2  cos . B cos C  2 1  cos B 2 1  cos C  2 2
 cos B  cos C 1 S Hay HDK 2 2 2
 cos A  cos B  cos C 1(dfcm) SABC
*Lời bình:Bài toán 10 có thể không cần ôn tập vì phần lớn lượng kiến thức nằm ở phần đại số lớp 10* Trang 7