Đề thi thử vào 10 môn Toán của Phòng GD Nông Cống 2024-2025 (có đáp án)
Tổng hợp đề thi thử Tuyển Sinh vào 10 môn TOÁN của Phòng GD Nông Cống năm học 2024-2025 có lời giải chi tiết. Đề thi được biên soạn dưới dạng file PDF gồm 2 trang giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2024-2025
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ VÀO LỚP 10 THPT HUYỆN NÔNG CỐNG NĂM HỌC: 2024-2025 MÔN: TOÁN
Thời gian làm bài:120 phút
(Không kể thời gian giao đề) Ngày thi:
Câu 1: ( 2 điểm) 1 𝑥−3
Cho biểu thức 𝐴 = ( √𝑥 + − ) . √𝑥+2 √𝑥−3 √𝑥+2 𝑥−√𝑥−6 √𝑥 1. Rút gọn biểu thức A 2
2. Tìm các giá trị của x để 𝐴 < − 3
Câu 2: ( 2 điểm) 3𝑥 + 5𝑦 = −1
1. Giải hệ phương trình { 7𝑥 − 3𝑦 = 5
2. Cho hàm số 𝑦 = 𝑎𝑥 + 𝑏 . Tìm 𝑎, 𝑏 biết đồ thị hàm số đó cắt trục tung tại
điểm có tung độ là -2 và cắt đường thẳng 𝑦 = −2𝑥 + 1 tại điểm có hoành độ là -1.
Câu 3: ( 2 điểm)
1. Giải phương trình −3𝑥2 + 4𝑥 + 7 = 0
2. Cho phương trình 𝑥2 + (2𝑚 − 3)𝑥 − 2(𝑚 − 1) = 0 với 𝑚 là tham số. Tìm 1 1 5
𝑚 để phương trình có hai nghiệm 𝑥1, 𝑥2 thỏa mãn: + = (𝑥1+1)2 (𝑥2+1)2 2
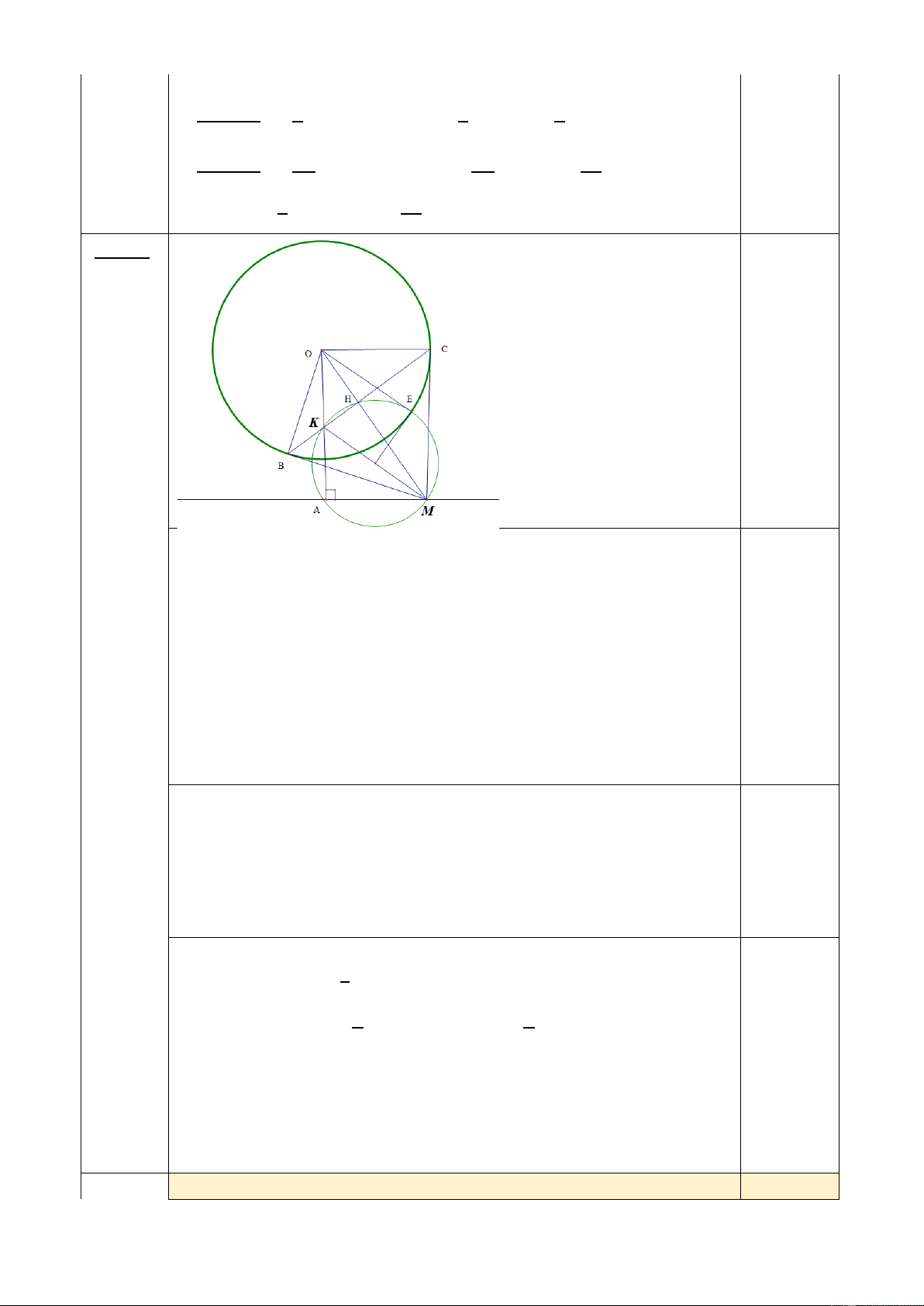
Câu 4: ( 3 điểm) Cho đường tròn tâm O và đường thẳng d nằm ngoài đường tròn.
Trên đường thẳng d lấy điểm M bất kỳ, từ M kẻ hai tiếp tuyến MB, MC với đường
tròn (B,C là các tiếp điểm). Kẻ OA vuông góc với đường thẳng d tại A, OM cắt
BC tại H, OA cắt BC tại K.
1. Chứng minh rằng bốn điểm H, K, A, M cùng thuộc một đường tròn và xác
định tâm I của đường tròn đó.
2. Gọi E là giao điểm của đường tròn (O) và (I). Chứng minh:
OA. OK = OB2 và OE là tiếp tuyến của đường tròn (I)
3. Tìm vị trí của điểm M trên đường thẳng d để diện tích tam giác OKH lớn nhất.
Câu 5: ( 1 điểm)
Cho 𝑥, 𝑦, 𝑧 là các số thực lớn hơn 2. Tìm giá trị nhỏ nhất của biểu thức: 𝑥 𝑦 𝑧 𝐴 = + + √𝑦 + 𝑧 − 4 √𝑥 + 𝑧 − 4 √𝑥 + 𝑦 − 4
----------------------------------------------Hết------------------------------------------- Trang 1
Họ và tên thí sinh:………………………………........ Số báo danh:………….. HƯỚNG DẪN CHẤM Câu Đáp án Thang điểm Câu 1: 1 𝑥−3
Cho biểu thức 𝐴 = ( √𝑥 + − ) . √𝑥+2 √𝑥−3 √𝑥+2 𝑥−√𝑥−6 √𝑥 1. Rút gọn biểu thức A ( 2 điểm) 2
2. Tìm các giá trị của x để 𝐴 < − 3 √𝑥 1 𝑥 − 3 √𝑥 + 2 𝐴 = ( + − ) . √𝑥 − 3 √𝑥 + 2 𝑥 − √𝑥 − 6 √𝑥 ĐK: 𝑥 > 0, 𝑥 ≠ 9 0.25
√𝑥. (√𝑥 + 2) + 1. (√𝑥 − 3) − (𝑥 − 3) √𝑥 + 2 0.25 𝐴 = . ( √𝑥 − 3)(√𝑥 + 2) √𝑥 3√𝑥 √𝑥 + 2 𝐴 = . (√𝑥 − 3)(√𝑥 + 2) √𝑥 3 0.25 𝐴 = √𝑥 − 3 3 Vậy 𝐴 =
với 𝑥 > 0, 𝑥 ≠ 9 0.25 √𝑥−3 2 3 2 Để 𝐴 < − thì
< − với 𝑥 > 0, 𝑥 ≠ 9 0.25 3 √𝑥−3 3 3 2 + <0 √𝑥−3 3 9+2( √𝑥−3) <0 3(√𝑥−3) 2 √𝑥+3 0.25 <0 3(√𝑥−3)
√𝑥 − 3 < 0 𝑣ì 2√𝑥 + 3 > 0 x<9 0.25 2
Vậy 0 < 𝑥 < 9 thì 𝐴 < − 0.25 3 Câu 2 3𝑥 + 5𝑦 = −1 ( 2 điểm)
1. Giải hệ phương trình { 7𝑥 − 3𝑦 = 5
2. Cho hàm số 𝑦 = 𝑎𝑥 + 𝑏(𝑎 ≠ 0) . Tìm 𝑎, 𝑏 biết đồ thị
hàm số đó cắt trục tung tại điểm có tung độ là -2 và cắt đường
thẳng 𝑦 = −2𝑥 + 1 tại điểm có hoành đội là -1. Trang 2 3𝑥 + 5𝑦 = −1 9𝑥 + 15𝑦 = −3 { <=> { 7𝑥 − 3𝑦 = 5 35𝑥 − 15𝑦 = 25 0.25 44𝑥 = 22 { 7𝑥 − 3𝑦 = 5 0.25 1 𝑥 = { 2 1 7. − 3𝑦 = 5 2 𝑥 = 0.5 { 𝑦 = −0.5 0.25 𝑥 = 0.5
Vậy hệ phương trình có nghiệm duy nhất { 𝑦 = −0.5 0.25
Điểm thuộc đường thẳng 𝑦 = −2𝑥 + 1 có hoành độ là -1 thì
tung độ là 𝑦 = −2. (−1) + 1 = 3 0.25
Vì đồ thị hàm số cắt trục tung tại điểm có tung độ là -2 nên
b=-2 => 𝑦 = 𝑎𝑥 − 2 0.25
Vì đường thẳng 𝑦 = −2𝑥 + 1 và đường thẳng 𝑦 = 𝑎𝑥 − 2 cắt
nhau tại điểm có hoành độ là -1 nên đường thẳng 𝑦 = 𝑎𝑥 − 2 đi qua điểm (-1;3) 3 = 𝑎. (−1) − 2 𝑎 = −5 0.25
Vậy 𝑎 = −5, 𝑏 = −2 0.25 Câu 3
1. Giải phương trình −3𝑥2 + 4𝑥 + 7 = 0 ( 2 điểm)
2. Cho phương trình 𝑥2 + (2𝑚 − 3)𝑥 − 2(𝑚 − 1) = 0
với 𝑚 là tham số. Tìm 𝑚 để phương trình có hai nghiệm 𝑥1, 𝑥2 1 1 5 thỏa mãn: + = (𝑥1+1)2 (𝑥2+1)2 2
−3𝑥2 + 4𝑥 + 7 = 0 ( a=-3, b=4, c=7) 0.25 Ta thấy a-b+c=-3-4+7=0 0.25
Phương trình có hai nghiệ 7 m 𝑥1 = −1, 𝑥2 = 0.25 3 7
Vậy phương trình đã cho có tập nghiệm 𝑆 = {−1; } 0.25 3
𝑥2 + (2𝑚 − 3)𝑥 − 2(𝑚 − 1) = 0(𝑎 = 1, 𝑏 = 2𝑚 − 3, 𝑐 = −2(𝑚 − 1)
Ta thấy 𝑎 + 𝑏 + 𝑐 = 1 + 2𝑚 − 3 − 2(𝑚 − 1) = 0
Phương trình có hai nghiệm 𝑥1 = 1, 𝑥2 = −2(𝑚 − 1) = −2𝑚 + 2 0.25 1 1 5 Theo bài ra + = (𝑥1+1)2 (𝑥2+1)2 2 1 1 5 + = (1+1)2 (−2𝑚+3)2 2 1 9 = (−2𝑚+3)2 4 1 3 1 −3 = hoặc = 0.25 −2𝑚+3 2 −2𝑚+3 2 Trang 3 1 3 2 7 +) = −2𝑚 + 3 = 𝑚 = 0.25 −2𝑚+3 2 3 6 1 −3 −2 11 +) = −2𝑚 + 3 = 𝑚 = 0.25 −2𝑚+3 2 3 6 7 11 Vậy 𝑚 = hoặc 𝑚 = 6 6 Câu 4: ( 3 điểm)
Ta có OB=OC ( Cùng bán kính)
MB=MC( Tính chất tiếp tuyến cắt nhau)
OM là đường trung trực của BC 𝐾𝐻𝑀 ̂ =900 Mà 𝐾𝐴𝑀 ̂ =900 (…) 𝐾𝐻𝑀 ̂ =𝐾𝐴𝑀 ̂ =900
H, A thuộc đường tròn đường kính KM 0.5
H, K,A,M thuộc đường tròn đường kính KM
Tâm I của đường tròn đi qua bốn điểm A, K, H, M là trung điểm của MK 0.5
Chứng minh được OK.OA=OH.OM 0.25 OB2=OH.OM =>OB2=OK.OA 0.25
Chứng minh ∆𝑂𝐸𝐾 ∽△ 𝑂𝐴𝐸 0.25 𝑂𝐸𝐾 ̂ = 𝑂𝐴𝐸 ̂
OE là tiếp tuyến của (I) 0.25
Ta có OB2=OK.OA =>… mà A, B cố định => K cố định 0.5 1 Diện tích ∆ OHK= OH.OK 2 1 1
≤ (𝑂𝐻2 + 𝐾𝐻2) = 𝑂𝐾2 4 4
Dấu “=” xẩy ra khi OH=KH=> góc HOK bằng 450
=> tam giác OAM vuông cân tại A => MA=OA
Vậy M thuộc đường thẳng d sao cho MA=AO thì diện tích tam 0.5 giác OHK lớn nhất
Cho 𝑥, 𝑦, 𝑧 là các số thực lớn hơn 2. Tìm giá trị nhỏ nhất của Trang 4 biểu thức: 𝑥 𝑦 𝑧 1 điể 𝐴 = + + m √𝑦 + 𝑧 − 4 √𝑥 + 𝑧 − 4 √𝑥 + 𝑦 − 4 Câu 5 4+𝑦+𝑧−4 𝑦+𝑧
Ta có 2. √𝑦 + 𝑧 − 4 ≤ = 2 2 𝑦+𝑧 √𝑦 + 𝑧 − 4 ≤ 4 𝑥 4𝑥 ≥ √𝑦+𝑧−4 𝑦+𝑧
Tương tự ta chứng minh được 𝑦 4𝑦 𝑧 4𝑧 ≥ , ≥ √𝑥+𝑧−4 𝑥+𝑧 √𝑥+𝑦−4 𝑥+𝑦 4𝑥 4𝑦 4𝑧 𝐴 ≥ + + 𝑦+𝑧 𝑥+𝑧 𝑥+𝑦 𝑥 𝑦 𝑧 𝐴 ≥ 4( + + ) 0.5 𝑦+𝑧 𝑥+𝑧 𝑥+𝑦
Học sinh chứng minh được 𝑥 𝑦 𝑧 3 + + ≥ 𝑦 + 𝑧 𝑥 + 𝑧 𝑥 + 𝑦 2 A≥ 6
Dấu “=” xẩy ra khi 𝑥 = 𝑦 = 𝑧 = 4
Vậy giá trị nhỏ nhất của biểu thức là 6 khi 𝑥 = 𝑦 = 𝑧 = 0.5 4 Trang 5