Đề thi thử vào 10 môn Toán năm 2021 – 2022 trường Khương Thượng – Hà Nội
Chủ Nhật ngày 06 tháng 06 năm 2021, trường THCS Khương Thượng, quận Đống Đa, thành phố Hà Nội tổ chức kỳ thi thử tuyển sinh vào lớp 10 THPT môn Toán năm học 2021 – 2022.
Đề thi thử vào 10 môn Toán năm 2021 – 2022 trường THCS Khương Thượng – Hà Nội gồm 01 trang với 05 bài toán dạng tự luận, thời gian làm bài 90 phút (theo cấu trúc mới của sở GD&ĐT Hà Nội); đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm. Mời bạn đọc đón xem !
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
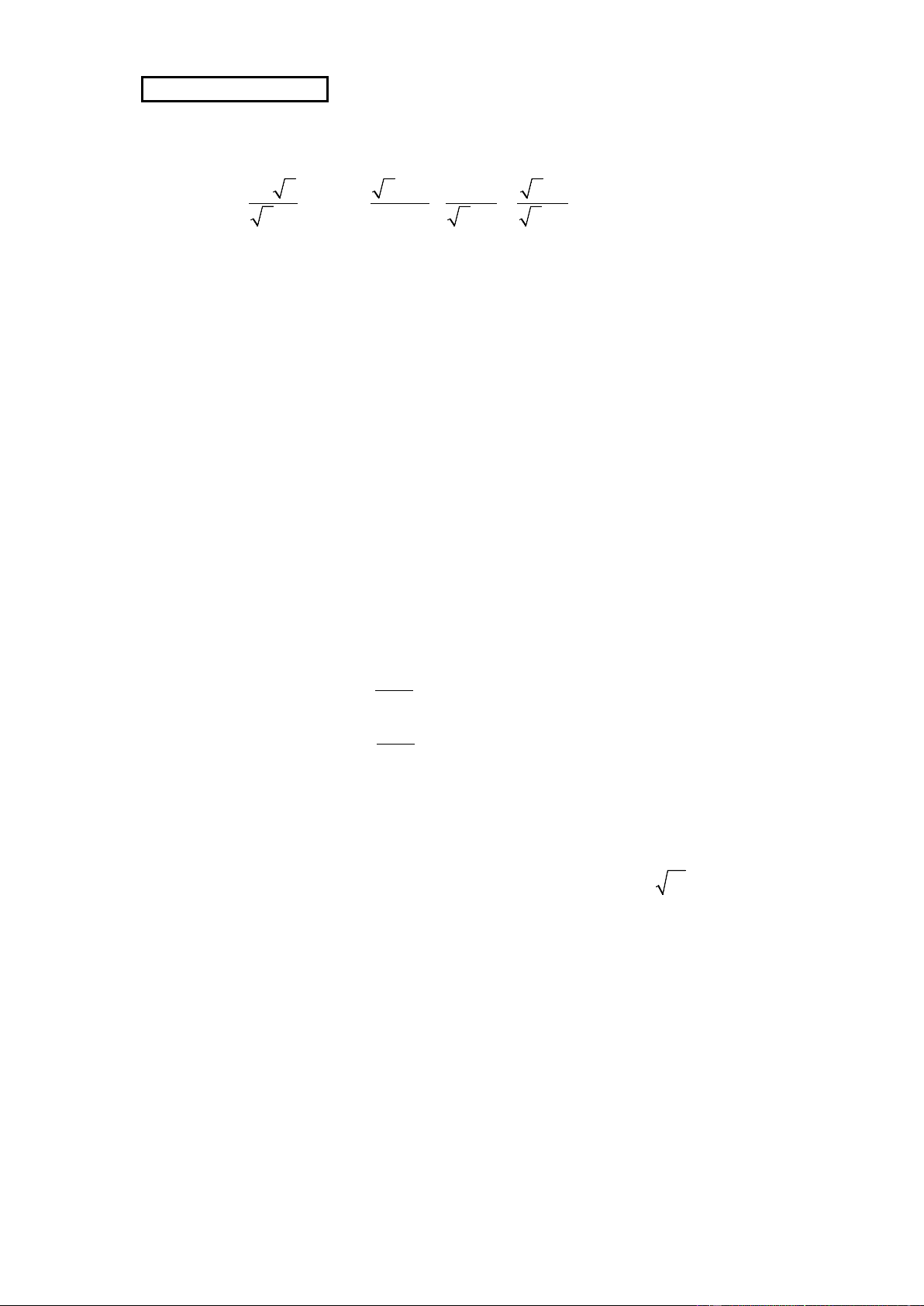
Preview text:
TRƯỜNG THCS KHƯƠNG THƯỢNG
ĐỀ THI THỬ VÀO LỚP 10 THPT
NĂM HỌC 2021 – 2022 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Ngày thi: 06 tháng 6 năm 2021
Thời gian làm bài: 90 phút
Bài I. (2,0 điểm) 1− x x −15 2 x +1
Cho hai biểu thức A = và B = + :
với x ≥ 0; x ≠ 25 x +1 25 − x x + 5 x − 5
1) Tính giá trị của A khi x = 9
2) Rút gọn biểu thức B
3) Tìm số thực x để biểu thức M = B − A nhận giá trị nguyên.
Bài II. (2,0 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một phân xưởng sản xuất thiết bị y tế theo kế hoạch phải sản xuất 1100 nhiệt kế điện tử phục vụ công tác
đo thân nhiệt để phòng chống dịch bệnh trong một thời gian quy định. Nhưng do tình hình dịch bệnh diễn
biến phức tạp, để đáp ứng nhu cầu nhiệt kế điện tử của thị trường, mỗi ngày phân xưởng đã sản xuất vượt
mức 5 nhiệt kế nên phân xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định là 2 ngày. Hỏi theo kế
hoạch mỗi ngày phân xưởng sản xuất bao nhiêu nhiệt kế điện tử?
2) Một chiếc nón lá hình nón có đường sinh bằng 20 cm, đường kính bằng 30 cm. Người ta dùng hai
lớp lá để phủ lên bề mặt xung quanh của nón. Tính diện tích lá cần dùng cho một chiếc nón đó.
Bài III. (2,5 điểm) (x− ) 2 3 2 − = 4 y + 3
1) Giải hệ phương trình (x − ) 1 2 2 + = 5 y + 3 2) Cho Parabol ( P) 2
: y = x và đường thẳng (d ) : y = 5x − m +1 với m là tham số.
a) Tìm tọa độ giao điểm của (d ) và ( P) khi m = 5 .
b) Tìm m để (d ) cắt (P) tại hai điểm có hoành độ x ; x thỏa mãn 2x = x 1 2 1 2
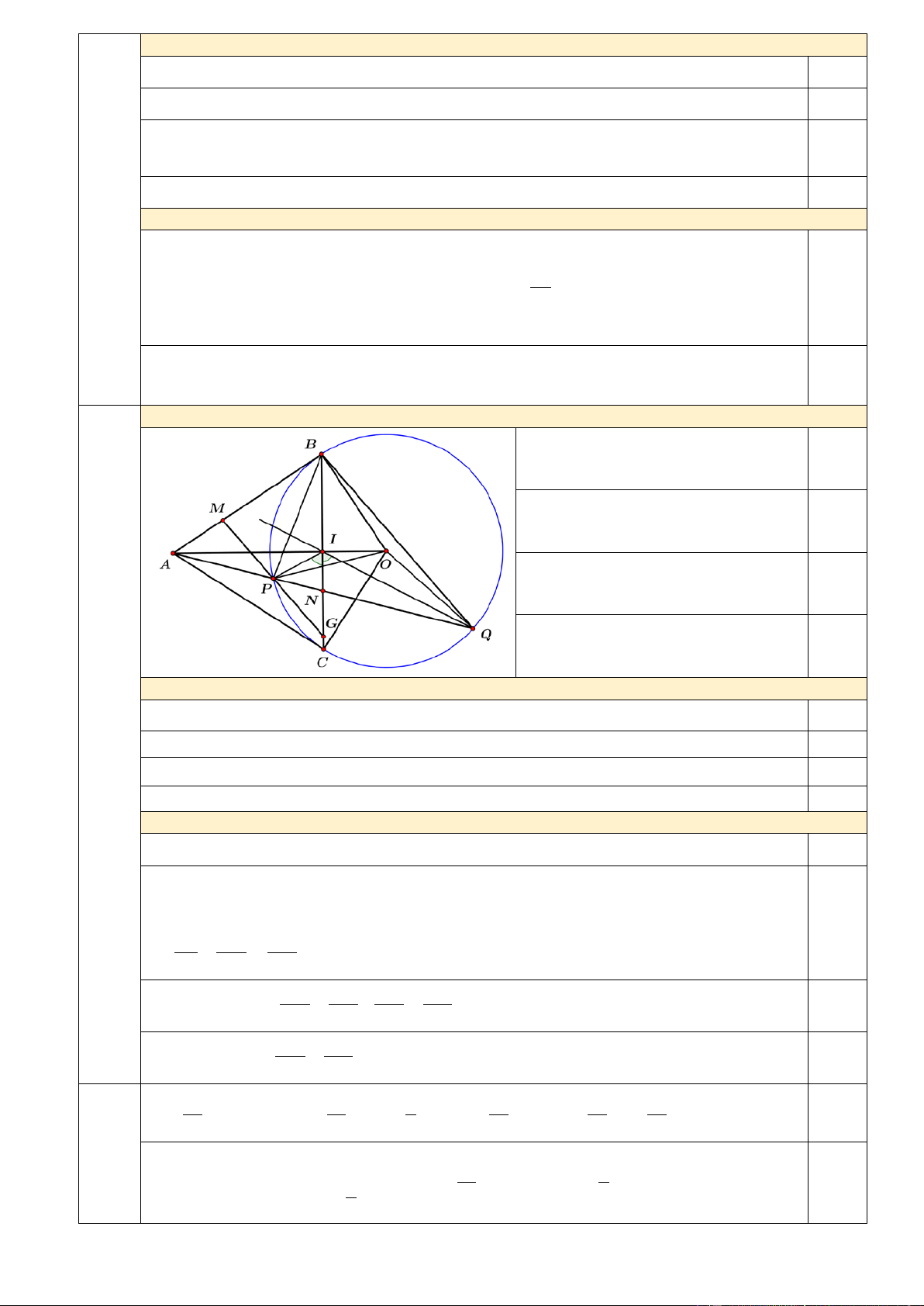
Bài IV. (3,0 điểm) Cho đường tròn (O). Từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC tới
đường tròn (O) với B, C là các tiếp điểm. Qua điểm A vẽ đường thẳng d không đi qua tâm cắt đường tròn
tại P, Q (P nằm giữa A và Q; P và Q cùng thuộc nửa mặt phẳng bờ là đường thẳng AO không chứa điểm
B). Gọi I là giao điểm của AO và BC.
1) Chứng minh: 4 điểm A, B, O, C cùng thuộc một đường tròn 2) Chứng minh: 2
AB = AI.AO . Từ đó suy ra: AI.AO=AP.AQ
3) Vẽ đường thẳng đi qua P và song song BQ cắt đường thẳng AB, BC theo thứ tự tại M, G. Chứng
minh: P là trung điểm của MG.
Bài IV. (0,5 điểm) Cho hai số thực x, y thỏa mãn x ≥ 1; x + y ≤ 4. Tìm giá trị nhỏ nhất của biểu thức 2 2
A = x + 3xy + 4 y
---------HẾT --------
HƯỚNG DẪN CHẤM ĐỀ THI THỬ VÀO 10 THPT
NĂM HỌC 2021 – 2022 Môn thi: TOÁN
Ngày thi: 06 tháng 6 năm 2021 Bài Nội dung Điểm 1) 0,5 điểm 1− 9
Thay x = 9 (tmđk) vào ,
A ta được A = 0,25 9 +1 1− 3 1 = = − 1
. Vậy A = − khi x = 9 0,25 3 +1 2 2 2) 1,0 điểm 15 − x 2 x − 5 B 0,25 ( = + x − 5)( x + 5) . x + 5 x +1 Bài I
15 − x + 2 x −10 x − 5 = . (2,0 ( 0,25 x + 5)( x − 5) x +1 điểm) x + 5 1 = . 0,25 x + 5 x +1 1 = 0,25 x +1 3) 0,5 điểm 1 1− x 1+ x −1 1 M = − = = 1− 0,25 x +1 x +1 x +1 x +1 1 Vì x ≥ 0 ⇒ 0 < ≤ 1. Do đó M nguyên 1 ⇔ = 1 ⇔ x = 0 0,25 x +1 x +1 1) 1,5 điểm
Gọi số nhiệt kế mà phân xưởng sản xuất mỗi ngày theo kế hoạch là x ( * x ∈ , nhiệt 0,25 kế)
Số nhiệt kế sản xuất thực tế là x + 5 (nhiệt kế) 0,25 1100
Thời gian sản xuất nhiệt kế theo kế hoạch là (ngày) 0,25 x 1100
Bài II Thời gian sản xuất nhiệt kế trong thực tế là (ngày) 0,25 (2,0 x + 5
điểm) Theo bài ra ta có phương trình: 1100 1100 − = 2 0,25 x x + 5
⇒ x = 50 (tmđk). Vậy số nhiệt kế phấn xưởng sản xuất theo kế hoạch là 50 (nhiệt kế) 0,25 2) 0,5 điểm 30
Diện tích xung quanh của chiếc nón lá hình nón là: S = π . .20 = 300π cm 0,25 xq ( 2) 2
Diện tích lá cần dùng cho một chiếc nón là: π = π ( 2 2.300 600 cm ) 0,25 1) 1,0 điểm Điề 1
u kiện: y ≠ 3 . Đặt a = x − 2;b = 0,25 y + 3 Bài III 3 a − 2b = 4 a = 2 (2,5 Ta có: ⇔ điể 0,50 m) 2a + b = 5 b = 1 x = 4 ⇒
. Vậy nghiệm của hệ phương trình là (4; 2 − ) 0,25 y = 2 − (tm) 2) a. 1,0 điểm
Với m = 5 ⇒ ( P) : y = 5x − 4 0,25
Xét phương trình hoành độ giao điểm của (d ) và (P) : 2 x = 5x − 4 0,25 x = 1 2
⇔ x − 5x + 4 = 0 ⇔ (x − )
1 ( x − 4) = 0 ⇔ 0,25 x = 4
Với x = 1 ⇒ y = 1; x = 4 ⇒ y = 16 . Vậy tọa độ giao điểm là (1; ) 1 và (4;16) 0,25 b. 0,5 điểm
Phương trình hoành độ giao điểm: 2
x − 5x + m −1 = 0 (*). 25 − 4m + 4 > 0 29 1 < m < 0,25
Yêu cầu bài toán ⇔ m −1 > 0 ⇔ 4 (**) 2 4x = x 20x − 4m + 4 = x 1 2 1 2 x + x = 5 Theo Vi ét 1 2
. Kết hợp với (**) ⇒ m = 5(tm) 0,25 x x = m −1 1 2 1) 1,0 điểm
Vẽ hình đúng đến ý 1) 0,25 0 ABO = 90 , 0 ACO = 90 (AB, AC là 0,25 tiếp tuyến) ⇒ ABO + 0
ACO = 180 . Mà B, C 0,25 đối nhau
⇒ tứ giác ABOC nội tiếp ⇒ 0,25 ,
A B, O, C cùng thuộc một ĐT 2) 1,0 điểm
Xét ∆ABO vuông tại B, ta có BC ⊥ AO = {I} 0,25 Bài IV (3,0 2
⇒ AB = AI.AO (hệ thức lượng trong tam giác vuông) 0,25
điểm) Ta có: 2 AB = A .
P AQ (AB tiếp tuyến, APQ là cát tuyến) 0,25
Suy ra AI.AO = A . P AQ (1) 0,25 3) 1,0 điểm
Từ (1) ⇒ tứ giác OIPQ nội tiếp ⇒ ∆API ∽ ∆AOQ ( g.g ) 0,25 = = = AIP OQP OPQ
OIQ (2 góc t.ư; ∆ cân; cùng chắn OQ ) ⇒ PIN = NIQ
⇒ IN là phân giác trong của
PIQ ; IA là phân giác ngoài của ∆PIQ tại I 0,25
⇒ PI = PN = AP (2) IQ NQ AQ MP AP PN PG
Mà MP / / BQ ⇒ = ; = (3) 0,25 BQ AQ NQ BQ MP PG Từ (2) và (3) ⇒ = ⇒ MP = PG 0,25 BQ BQ 2 9 7 3 7 7 7 2 2 2 2 A =
x + 3xy + 4 y + x = 4 x + y + x 2 ≥ 4.0 + .1 = 0,25 16 16 8 16 16 16 Bài V (0,5 x = 1 điểm) 7 3 Dấu “=” xảy ra ⇔ 3 . Vậy A =
khi x = 1; y = − 0,25 y = − min 16 8 8