
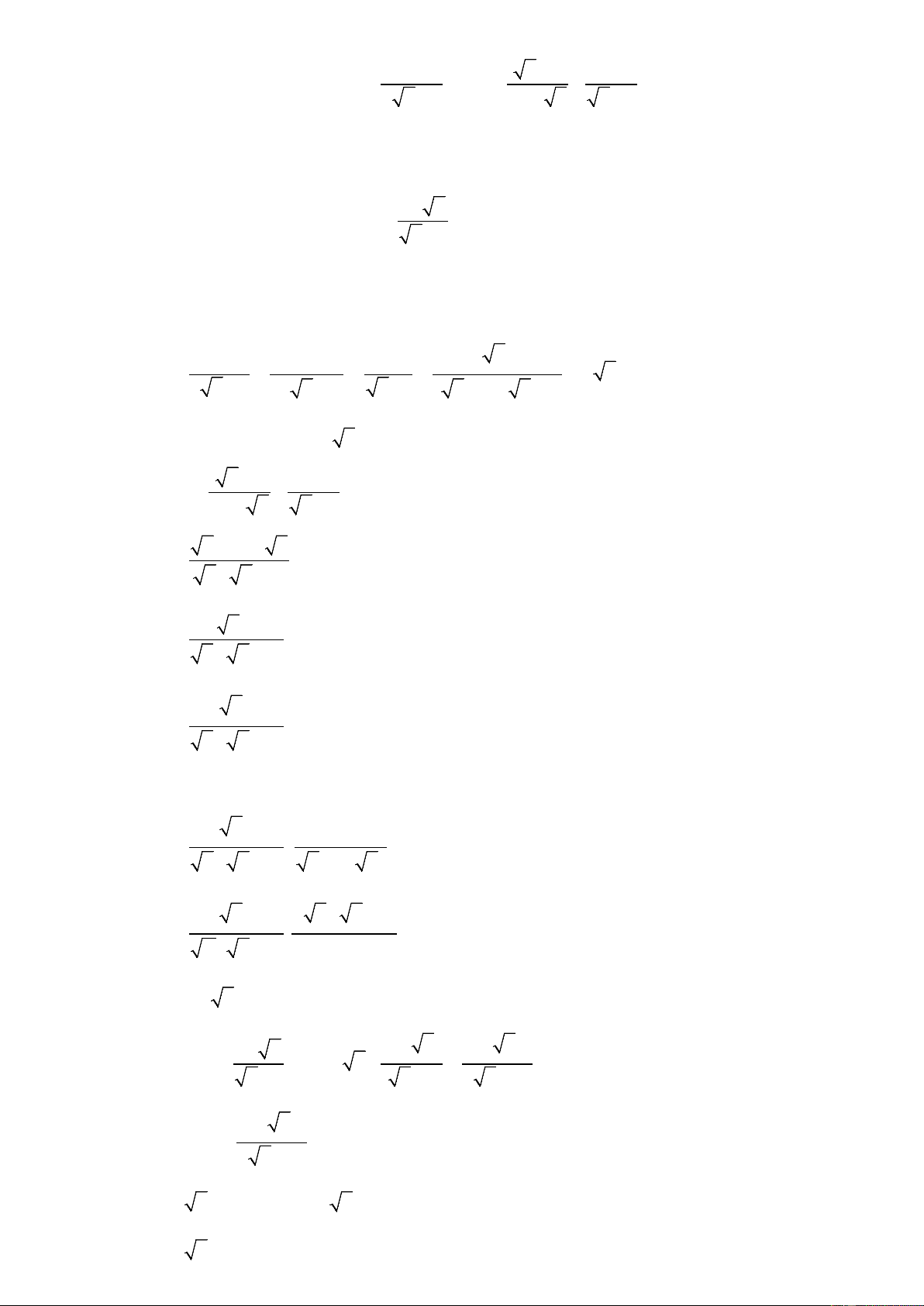

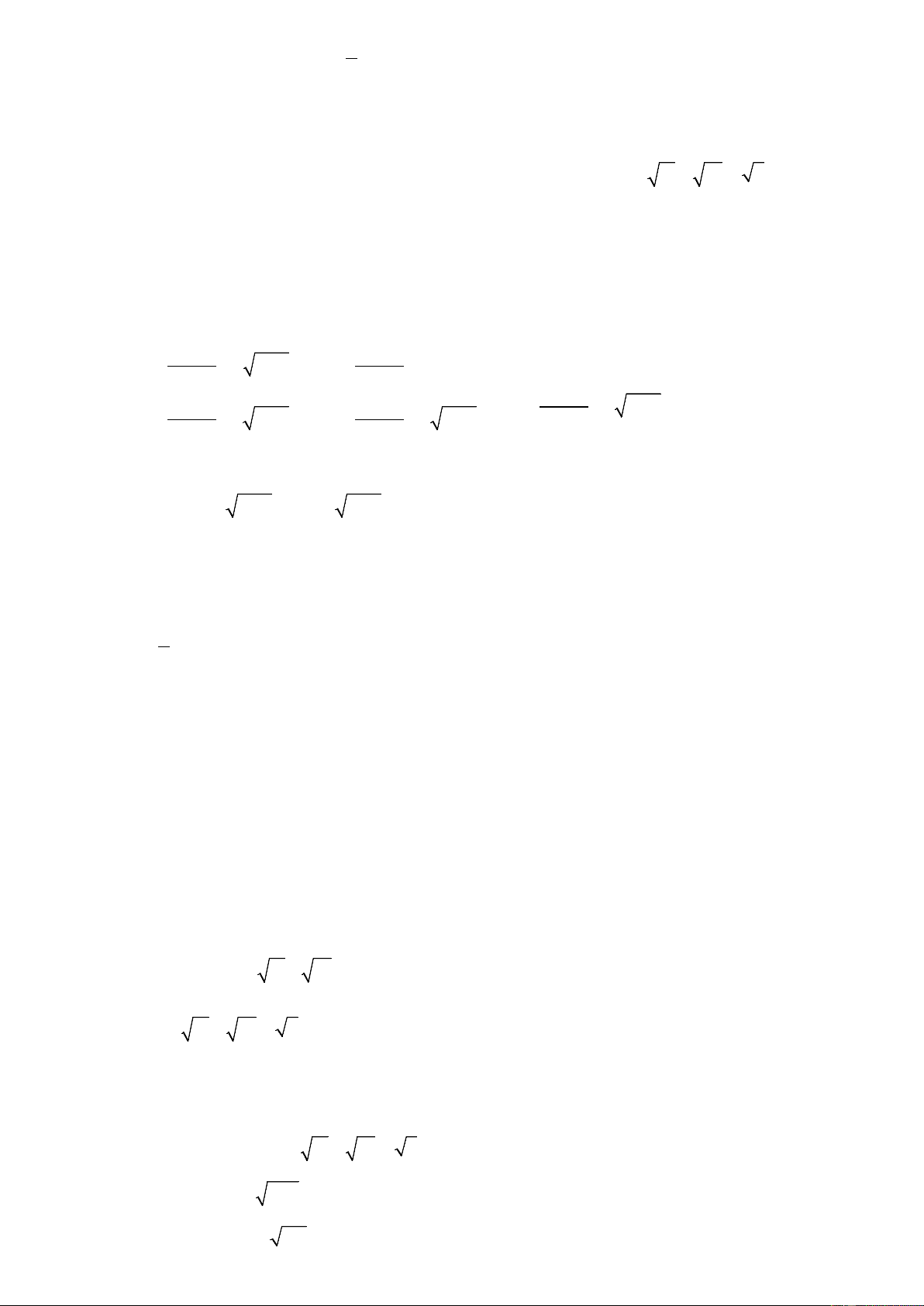
Preview text:
UBND QUẬN NAM TỪ LIÊM
ĐỀ THI THỬ VÀO 10 THPT NĂM HỌC 2021 – 2022
TRƯỜNG THCS MỸ ĐÌNH 2 MÔN THI: TOÁN
Ngày thi: 30 tháng 5 năm 2021
Thời gian làm bài: 90 phút 4 x − 4 3
Bài 1 (2,0 điểm:) Cho biểu thức A = và B = +
với x > 0, x ≠ 4 . 2 x − x x − 2 x x − 2
1) Tính giá trị của biểu thức A khi x = 2 . 2) Rút gọn P = B : A . 1− x
3) Tìm x để M ≥ 0 với M = . P . x − 3
Bài 2 (2,5 điểm):
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai địa điểm A và B cách nhau 30km . Cùng lúc, một người đi xe máy khởi hành từ A , một
người đi xe đạp khởi hành từ B . Nếu đi ngược chiều thì sau 40 phút họ gặp nhau. nếu đi cùng chiều
theo hướng từ A đến B thì sau 2 giờ họ gặp nhau tại địa điểm C ( B ở giữa A và C ). Tính vận tốc mỗi xe.
2) Một hình trụ có chiều cao bằng đường kính đáy, diện tích toàn phần của hình trụ là 2 48π (cm ) . Tính thể tích hình trụ đó.
Bài 3 (2,0 điểm): 2 + y −1 = 3 x −2y
1) Giải hệ phương trình : . 3 − 2 y −1 = 1 x − 2y 1 2) Cho parabol ( P) : 2 y =
x và đường thẳng (d ) : y = (m + )
1 x − m ( m là tham số, x là ẩn số). 2
a) Chứng minh (d ) luôn cắt ( P) tại hai điểm phân biệt với mọi m .
b) Gọi x ; x là hoành độ giao điểm của (d ) và ( P) . Tìm m để x + x = 2 . 1 2 1 2
Bài 4(3,0 điểm): Cho nửa đường tròn ( ;
O R) đường kính BC . Lấy điểm D và E di động trên nửa đường tròn sao cho
EOD = 90° ( D thuộc
CE , E thuộc
BD ); BD cắt CE tại H , các tia BE và CD
cắt nhau tại A .
a) Chứng minh tứ giác ADHE nội tiếp đường tròn.
b) Chứng minh OD là tiếp tuyến của đường tròn ngoại tiếp tứ giác ADHE .
c) Kẻ đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AC tại C . Gọi K
là giao điểm hai đường thẳng này và I là trung điểm AK . Tính số đo góc BIC .
d) Tìm vị trí điểm D và E trên nửa đường tròn ( ;
O R) để AB + AC lớn nhất.
Bài 5 (0,5 điểm): Cho các số ; x y thỏa mãn 2 2
x + 2xy + 3y = 6 . Tìm giá trị lớn nhất và giá trị nhỏ nhất
của M = x + 2 y . -------HẾT------- HƯỚNG DẪN 4 x − 4 3 Bài 1
(2,0 điểm) Cho biểu thức A = và B = +
với x > 0, x ≠ 4 2 x − x x − 2 x x − 2
1) Tính giá trị của biểu thức A khi x = 2
2) Rút gọn P = B : A 1− x
3) Tìm x để M ≥ 0 với M = . P x − 3 Lời giải
1) Khi x = 2 (tm) thay vào A ta có : 2.( 2 + ) 4 4 2 1 A = = = = = 2 2 + 2 2 2 − 2 2 ( 2 − ) 1 2 −1 ( 2 − )1.( 2 + )1
Vậy khi x = 2 thì A = 2 2 + 2 x − 4 3 2) B = + x − 2 x x − 2 x − 4 + 3 = x B x.( x − 2) 4 x − 4 B = x.( x − 2) 4 ( x − ) 1 B = x.( x − 2)
P = B : A 4 ( x − ) 1 4 P = x ( x − ) : . 2 x (2 − x ) 4 ( x − ) 1 − x.( x − 2) P = . x ( x − 2) . 4 P = 1− x − x − 1− x x 3) M = . P = ( − x ) ( ) ( )2 1 1 1 . = x − 3 x − 3 x − 3 ( − x)2 1 M ≥ 0 ⇔
≥ 0 (điều kiện x ≠ 9 ) x − 3
⇔ x − 3 > 0 (Vì ( − x)2 1
≥ 0 với x > 0, x ≠ 4, x ≠ 9 ) ⇔ x > 3 ⇔ x > 9 (TMĐK)
Vậy với x > 9 thì M ≥ 0 . Bài 2. (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Hai địa điểm A và B cách nhau 30km . Cùng lúc một người đi xe máy khởi hành từ A ,
một người đi xe đạp khởi hành từ B . Nếu đi ngược chiều thì sau 40 phút họ gặp nhau. nếu đi
cùng chiều theo hướng từ A đến B thì sau 2 giờ họ gặp nhau tại C ( B ở giữa A và C ). Tính vận tốc mỗi xe. Lời giải
Gọi vận tốc người đi xe máy khởi hành từ A , vận tốc người đi xe đạp khởi hành từ B lần lượt
là x ; y (km / h) x > 0; y > 0 .
Khi 2 người đi ngược chiều gặp nhau:
Quãng đường người đi từ 2 2 A sau 40 phút =
giờ gặp nhau là: x (km). 3 3
Quãng đường người đi từ 2 2 B sau 40 phút = giờ gặp nhau là: y (km). 3 3 Ta có phương trình 2 2 : x + y = 30 (1) 3 3
Khi 2 người đi cùng chiều gặp nhau:
Quãng đường người đi từ A đến C sau 2 giờ là 2x (km) , Quãng đường người đi từ B đến C
sau 2 giờ là 2 y (km) . Vì hai địa điểm A và B cách nhau 30 km, nên ta có phương trình:
2x − 30 = 2 y (2) . 2 2
x + y = 30 (1) x = 30 (tm)
Giải hệ phương trình 3 3 . Ta được . y =15 (tm)
2x − 30 = 2y (2)
Vậy vân tốc một người đi xe máy khởi hành từ A là 30 km / h , vân tốc một người đi xe đạp
khởi hành từ B là 15 km / h .
2) Một hình trụ có chiều cao bằng đường kính dây, diện tích toàn phần của hình trụ là 2
48π (cm ) . Tính thể tích hình trụ đó. Lời giải Ta có h = 2r .
Diện tích toàn phần hình trụ 2 2
2π r(h + r) = 6π r = 48π (cm ) 2
⇒ r = 8⇒ r = 2 2 (cm) . Thể tích hình trụ là: 2 3
π r h = π.8.2.2 2 = 32 2(cm ) . Bài 3.
(2,0 điểm) 2 + y −1 = 3 x −2y
1) Giải hệ phương trình : 3 − 2 y −1 = 1 x − 2y 1
2) Cho parabol ( P) : 2 y =
x và đường thẳng (d ) : y = (m + )
1 x − m ( m là tham số, x là ẩn 2 số)
a) Chứng minh (d ) luôn cắt ( P) tại hai điểm phân biệt với mọi m .
b) Gọi x ; x là hoành độ giao điểm của (d ) và ( P) . Tìm m để x + x = 2 1 2 1 2 Lời giải x ≠ 2y
1) Điều kiện xác định: y ≥ 1
Với điều kiện, hệ phương trình đã cho tương đương: 4 7 + 2 y −1 = 6 = 7 x − 2y = 1 x − 2y x − 2y ⇔ ⇔ 3 3 3 − 2 y −1 = 1 2 y 1 1 2 y 1 1 − − = − − = x − 2 y x − 2y x − 2y x = 2y +1 x = 2y +1 x = 2y +1 x = 5 ⇔ ⇔ ⇔ ⇔ (thỏa mãn điều kiện) 3 − 2 y −1 = 1 y −1 = 1 y −1 = 1 y = 2
Vậy hệ phương trình đã cho có nghiệm duy nhất ( ; x y ) = (5; 2) .
2) Phương trình hoành độ giao điểm của đường thẳng (d ) và parabol ( P) : 1 2 x = (m + ) 2
1 x − m ⇔ x − 2 (m + ) 1 x + 2m = 0 ( ) 1 2 Ta có ∆ = − (m + ) 2 2 '
1 − 2m = m +1
> 0 ∀m nên phương trình ( )
1 luôn có hai nghiệm phân biệt.
Do đó (d ) luôn cắt (P) tại hai điểm phân biệt với mọi m .
b) Theo kết quả câu a) ta có (d ) luôn cắt ( P) tại hai điểm phân biệt có hoành độ giao điểm là
x ; x với mọi m 1 2
x + x = 2 m +1 1 2 ( )
Áp dụng hệ thức Vi-et ta có : x .x = 2 m 1 2 x ≥ Điề 0
u kiện để x ; x có nghĩa là 1 . 1 2 x ≥ 0 2 Vì x + x =
2 nên x ; x không đồng thời bằng 0 1 2 1 2 x + x > 0 2 m +1 > 0 m > 1 − 1 2 ( ) Suy ra ⇔ ⇔ ⇔ m ≥ 0 x .x ≥ 0 2m ≥ 0 m ≥ 0 1 2
Theo đề bài ta có : x + x = 2 1 2
⇔ x + x + 2 x x = 2 1 2 1 2 ⇔ 2(m + ) 1 + 2 2m = 2
⇔ m + 2. m = 0
⇔ m ( m + 2) = 0
⇔ m = 0 (Vì m ≥ 0 nên m + 2 > 0 )
⇔ m = 0 (thỏa mãn điều kiện)
Vậy m = 0 là giá trị cần tìm. Bài 4. (3,0 điểm)
Cho nửa đường tròn ( ;
O R) đường kính BC . Lấy điểm D và E di động trên nửa đường tròn sao cho
EOD = 90° ( D thuộc
CE , E thuộc
BD ); BD cắt CE tại H , các tia BE và CD cắt nhau tại A .
a) Chứng minh tứ giác ADHE nội tiếp đường tròn.
b) Chứng minh OD là tiếp tuyến của đường tròn ngoại tiếp tứ giác ADHE .
c) Kẻ đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AC tại C . Gọi K
là giao điểm hai đường thẳng này và I là trung điểm AK . Tính số đo góc BIC .
d) Tìm vị trí điểm D và E trên nửa đường tròn ( ;
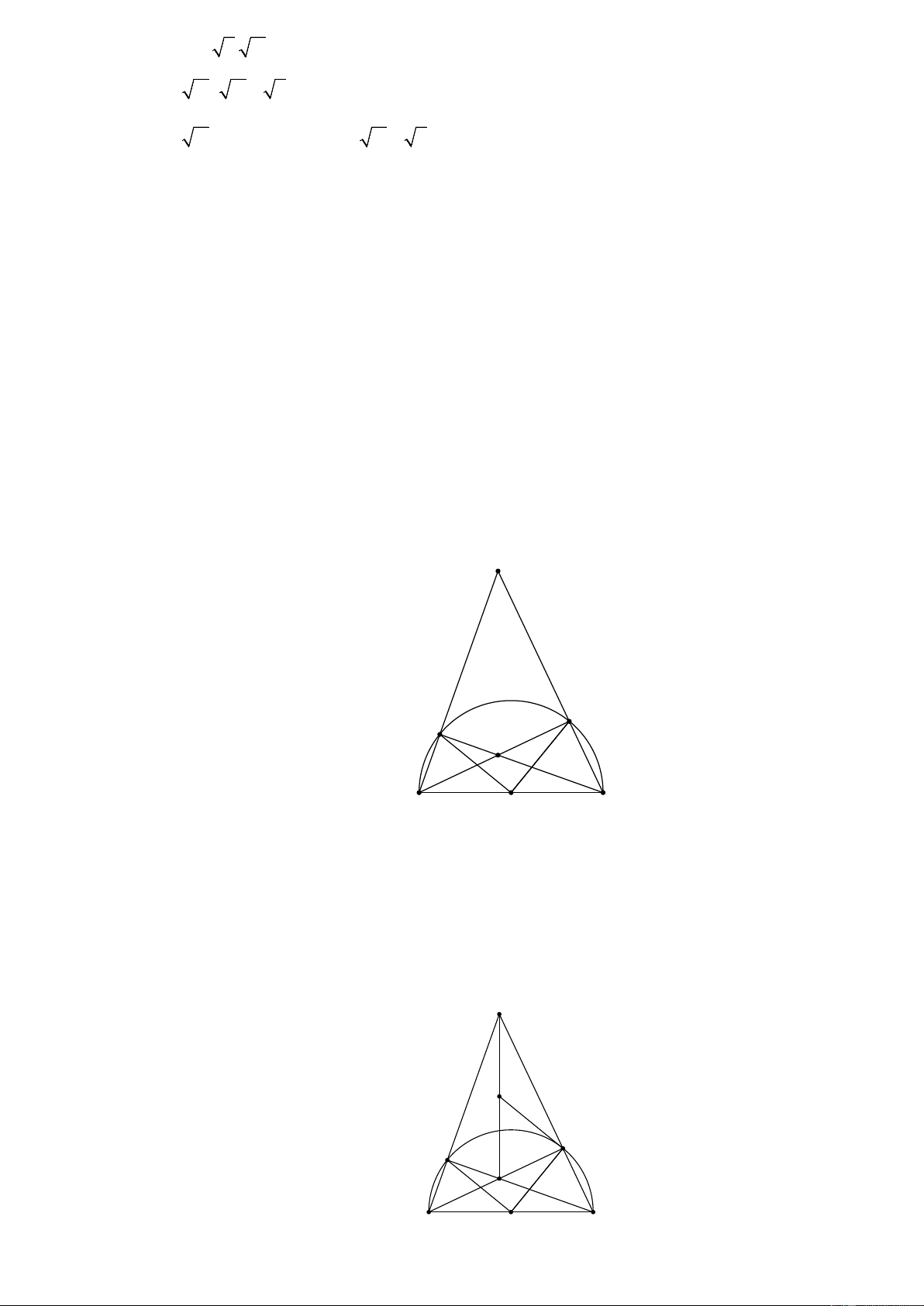
O R) để AB + AC lớn nhất. Lời giải A D E H B O C
a) Chứng minh tứ giác ADHE nội tiếp đường tròn. Ta có BEC =
BDC = 90° (các góc nội tiếp chắn nửa đường tròn) ⇒ AEH = ADH = 90° (kề
bù với các góc vuông); Tứ giác ADHE có AEH =
ADH = 90° nên nội tiếp đường tròn đường kính AH .
b) Chứng minh OD là tiếp tuyến của đường tròn ngoại tiếp tứ giác ADHE . A M D E H B O C
Gọi M là trung điểm AH ⇒ M là tâm đường tròn ngoại tiếp tứ giác ADHE ⇒ MD = MA
⇒ ∆MDA cân tại M ⇒ MDA = MAD ;
∆ODC cân tại O ⇒ ODC = OCD ; Vì BEC =
BDC = 90° (góc nội tiếp chắn nửa đường tròn) ⇒ CE ⊥ A ;
B BD ⊥ AC ⇒ ∆ABC có
hai đường cao BD,CE cắt nhau tại H ⇒ H là trực tâm của ∆ABC ⇒ AH cũng là đường cao
của ∆ABC ⇒ AH ⊥ BC ⇒ ODC + MDA = 90° ⇒ ODC + MDA = 90° ⇒ ODM = ° − ODC + 180 (
MDA) =180° − 90° = 90° ⇒ OD ⊥ MD tại D ⇒ OD là tiếp tuyến
của đường tròn ngoại tiếp tứ giác ADHE .
c) Kẻ đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AC tại C . Gọi K
là giao điểm hai đường thẳng này và I là trung điểm AK . Tính số đo góc BIC . A M I D E H B O C K Ta có ABK =
ACK = 90°(GT ) ⇒ tứ giác ABKC nội tiếp đường tròn đường kính AK có tâm
I là trung điểm của AK ⇒ BIC = 2.BAC ; DOE = °(GT ) ⇒ 90 sd DE = 90° ; 1 1
BAC là góc có đỉnh ngoài đường tròn ⇒ BAC = sd BC − (
sd DE ) = (180° − 90°) = 45° ; 2 2 ⇒ BIC =
2.BAC = 2.45° = 90° ; Vậy BIC = 90° .
d) Tìm vị trí điểm D và E trên nửa đường tròn ( ;
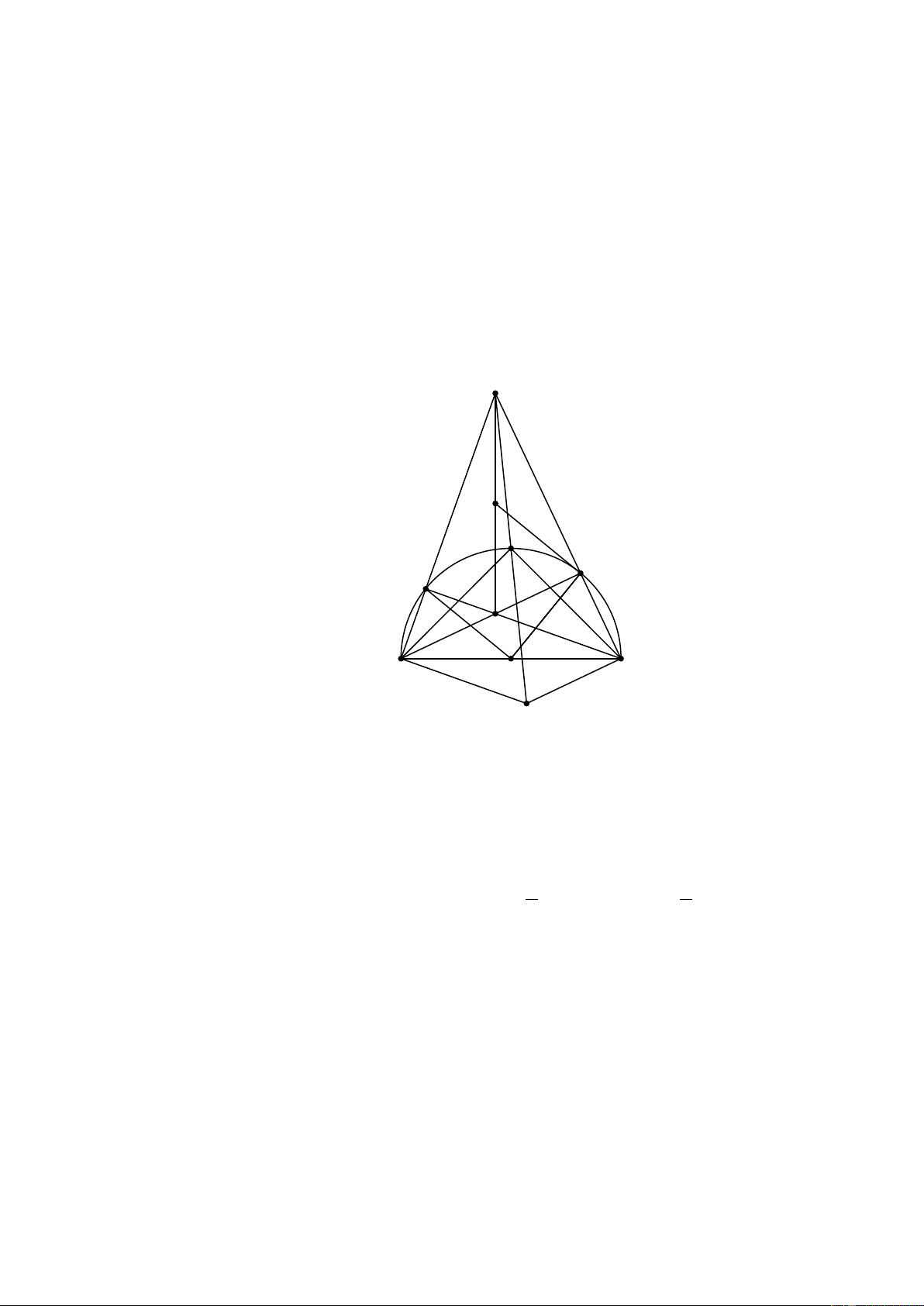
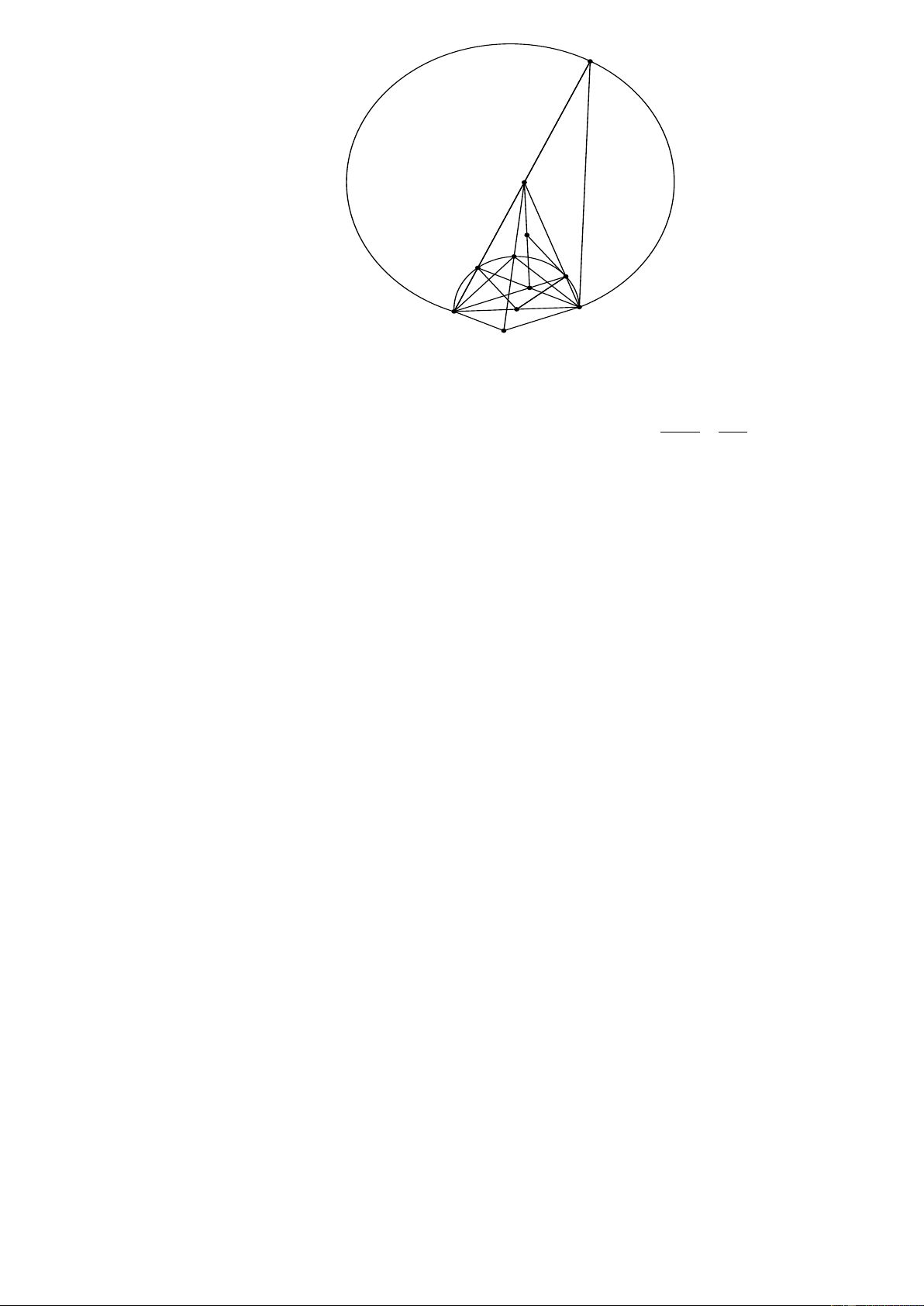
O R) để AB + AC lớn nhất. F A M I E D H C B O K
Trên tia đối của tia AB lấy điểm F sao cho AF = AC ⇒ ∆AFC cân tại A ⇒ AFC = ACF BAC ° có
BAC = 45° là góc ngoài của ∆AFC ⇒ BAC = AFC ⇒ 45 2. AFC = = = 22,5°; 2 2
Điểm F nhìn đoạn BC cố định dưới góc 22,5° không đổi nên điểm F thuộc cung chứa góc
22, 5° dựng trên đoạn BC cố định, từ đó AB + AC = AB + AF = BF lớn nhất khi BF là
đường kính của cung tròn này ⇒
BCF = 90° ⇒ ∆FBC vuông tại C mà
AF = AC ⇒ AF = AC = AB ⇒ ∆ABC cân tại A ⇒ ,
A H , I , O thẳng hàng ⇒ D, E lần lượt là
điểm chính giữa các cung: IC, IB .
Với I là điểm chính giữa
BC , AB + AC lớn nhất khi D, E lần lượt là điểm chính giữa các cung: IC, IB . Bài 5.
(0,5 điểm) Cho các số ; x y thỏa mãn 2 2
x + 2xy + 3y = 6 . Tìm giá trị lớn nhất và giá trị nhỏ nhất
của M = x + 2 y . Lời giải
M = x + 2 y ⇒ x = M − 2 y . 2 2
x + 2xy + 3y = 6 (1)
⇔ (M − y)2 + (M − y) 2 2 2 2 y + 3y = 6 2 2 2 2
⇔ M − 4My + 4y + 2My − 4y + 3y = 6 2 2
⇔ 3y − 2My + M − 6 = 0 (*) Để ( )
1 thỏa mãn thì (*) có nghiệm 2 ⇔ M − ( 2 3 M − 6) ≥ 0 2 ⇔ 2 − M +18 ≥ 0 ⇔ 3 − ≤ M ≤ 3 . GTNN Min M = 3 − khi x = 1 − ; y = 1 −
GTLN Max M = 3 khi x = 1; y = 1
Document Outline
- TRƯỜNG THCS MỸ ĐÌNH 2
- Thời gian làm bài: 90 phút
- Bài 1 (2,0 điểm:) Cho biểu thức và với .
- Bài 2 (2,5 điểm):
- Bài 3 (2,0 điểm):
- Bài 4(3,0 điểm): Cho nửa đường tròn đường kính . Lấy điểm và di động trên nửa đường tròn sao cho ( thuộc , thuộc ); cắt tại
- Bài 5 (0,5 điểm): Cho các số thỏa mãn . Tìm giá trị lớn nhất và giá trị nhỏ nhất của .
- -------HẾT-------
- ĐỀ KHẢO SÁT CHẤT LƯỢNG THI VÀO 10
- Bài 1 (2,0 điểm) Cho biểu thức và với
- Bài 2. (2,5 điểm)
- Bài 3. (2,0 điểm)
- Bài 4. (3,0 điểm)
- Bài 5. (0,5 điểm) Cho các số thỏa mãn . Tìm giá trị lớn nhất và giá trị nhỏ nhất của .




