Đề thi thử vào 10 năm 2020 – 2021 môn Toán trường THCS Thi Văn Tám – Long An

PHÒNG GD&ĐT ĐỨC HÒA KỲ THI TUYỂN SINH LỚP 10 NĂM HỌC 2020  2021
TRƯỜNG THCS THI VĂN TÁM Môn thi: TOÁN (CÔNG LẬP) Ngày thi: 17 / 07 / 2020 ĐỀ THI THỬ
Thời gian: 120 phút (không kể thời gian giao đề). Câu I: (1,5 điểm)
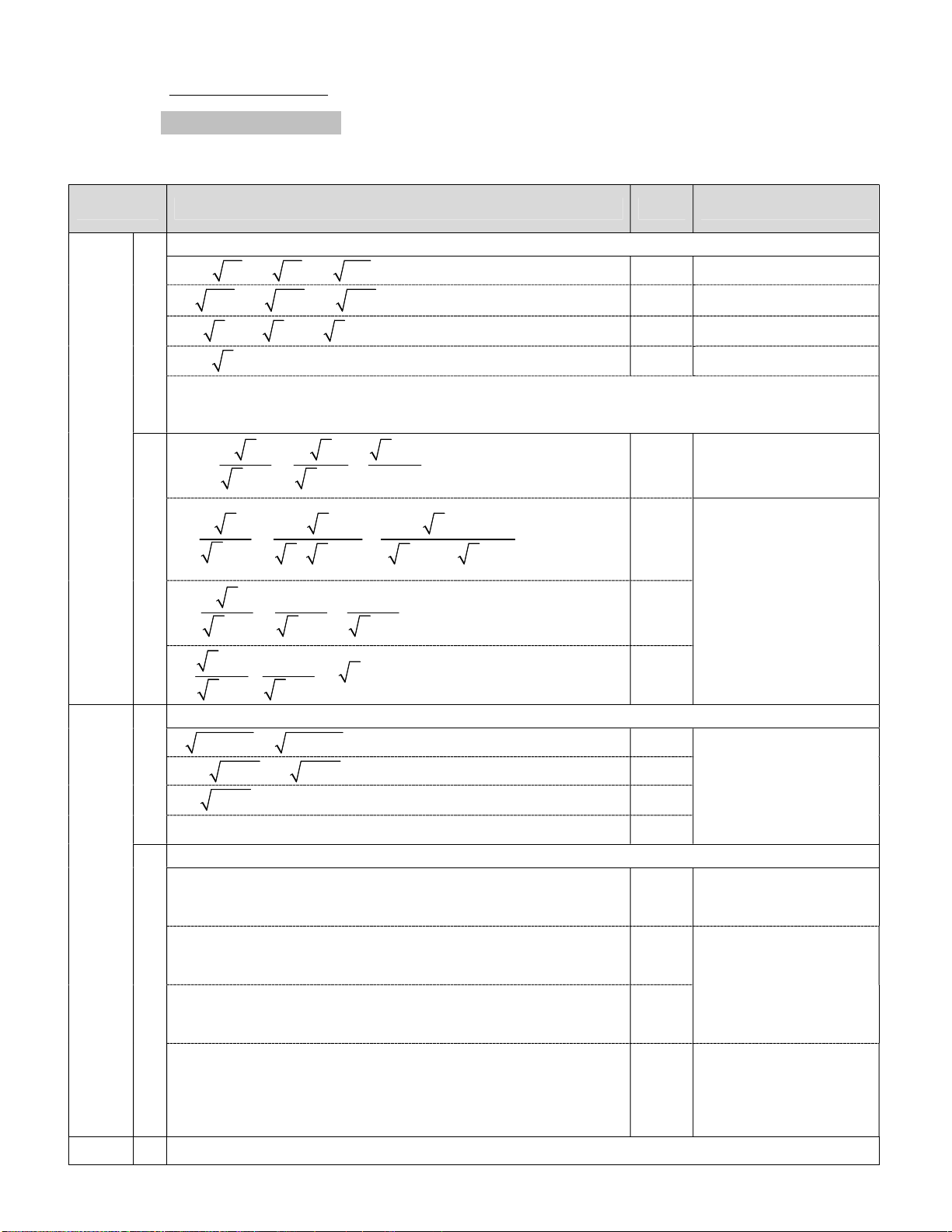
Rút gọn các biểu thức sau:
1. A  28  4 63  7 112.   2.  x x  x B  1     :  (với 0  x  1).  x 1 x  x  x 1  Câu II: (1,5 điểm)
1. Giải phương trình sau: 2 4x  20  9x  45  2.  x 2  y 2  8
2. Giải hệ phương trình sau:   x 3  y 2  3  .  Câu III: (2 điểm)
Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) : y  2x  1.
1. Vẽ (d). Tìm tọa độ giao điểm của (d) và (d ) : y  x   7 bằng phép tính. 1
2. Viết phương trình đường thẳng (d ') : y  ax b biết (d') song song với (d) và cắt trục
tung tại điểm F có tung độ là 2.
3. Cho hai đường thẳng sau: (d ) : y  2x  2020 , (d ) : y  3x  1. Nêu vị trí tương đối 2 3
của (d) và (d ); (d) và (d ). 2 3 Câu IV: (1,5 điểm)
Cho tam giác ABC vuông tại A có đường cao AH , biết độ dài AH  , 4 c 8 m , AB  c 6 m . Tính độ dài BH,BC và  tan ACH. Câu V: (2,5 điểm)
Cho đường tròn tâm O đường kính AB , C là điểm thuộc đường tròn (CA  CB). Tiếp
tuyến tại A của đường tròn (O) cắt BC tại D . Vẽ dây AE vuông góc với OD tại F .
a) Chứng minh AC  DB và các điểm A,F,C,D cùng thuộc một đường tròn.
b) Chứng minh DE là tiếp tuyến của đường tròn (O).
c) Đường thẳng qua E vuông góc với AB tại K cắt BC tại H . Chứng minh HF //AB. Câu VI: (1,0 điểm)
Tìm giá trị nhỏ nhất của biểu thức: P   x2 2020 1 x 0  26. __________HẾT__________
(Thí sinh được sử dụng máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm).
Họ và tên thí sinh:…………………………….Số báo danh:…………….........................................
Chữ kí CBCT 1:………………………...........Chữ kí CBCT 2:…………......................................... PHÒNG GD&ĐT ĐỨC HÒA K Ỳ T H I T U Y Ể N S I N H L Ớ P 1 0 N Ă M H Ọ C 2 0 2 0  2 0 2 1
TRƯỜNG THCS THI VĂN TÁM Môn thi: TOÁN (CÔNG LẬP) Ngày thi: 17 / 07 / 2020 HƯỚNG DẪN GIẢI
Thời gian: 120 phút (không kể thời gian giao đề).
(Hướng dẫn giải có 03 trang) Câu Đáp án Điểm Ghi chú
Rút gọn các biểu thức sau: A  28  4 63  7 112.  2  2  2 2 .7 4 3 .7 7 4 .7 0,25 1  2 7 12 7  28 7 0,25  18 7 0,25
HS không làm bước 1 và 2 hoặc bấm máy tính ra ngay kết quả thì không chấm điểm;ở bước 1 HS làm đúng
1 hạng tử thì vẫn được 0,25đ , tương tự ở bước 2;dấu “=” mà ghi dấu “  ” thì trừ 0,25đ. Thiếu hết các
dấu “=” thì không chấm điểm. HS chỉ làm bước 2 và 3 thì được 0,5đ.   I  x x  x B  1     : (với 0  x  1). (1,5đ)  x 1 x  x  x 1     x x  x      1  : 0,25  x 1 x  x   1  1 . 1 
  x    x   2 Dấu “=” mà ghi dấu
“  ” thì trừ 0,25đ.  x  1  1       : 0,25
Thiếu hết các dấu “=” thì  x 1 x 1 x 1 không chấm điểm. x  1 1  :  x  1. 0,25 x 1 x 1 Giải phương trình sau:
2 4x  20  9x  45  2.
- Dấu “  ”mà ghi dấu
“=” không chấm điểm.
1  4 x  5  3 x  5  2 0,25
- Ghi dấu “  ” thì không trừ điểm.
 x  5  2 (với x  5) 0,25 - Không ghi x  5 thì
 x  9 . Vậy phương trình có tập nghiệm: S  {9}. 0,25
chỉ đạt 0,25đ toàn bài.
Giải hệ phương trình sau:  x 2  y 2  8  II  x 3  y 2  3  .  (1,5đ)  x 5   5    x 2  y 2  0,25
- Chỉ có kết quả không có  8 bước thực hiện không 2 chấm. x   1
- Tìm được giá trị x hoặc    0,25 y chấm 0,5đ. 2.1  y 2   8 x    1  y    3 0,25
- Không có kết luận không đạt điểm bước này.
Vậy hệ phương trình có nghiệm duy nhất 1;  3 .
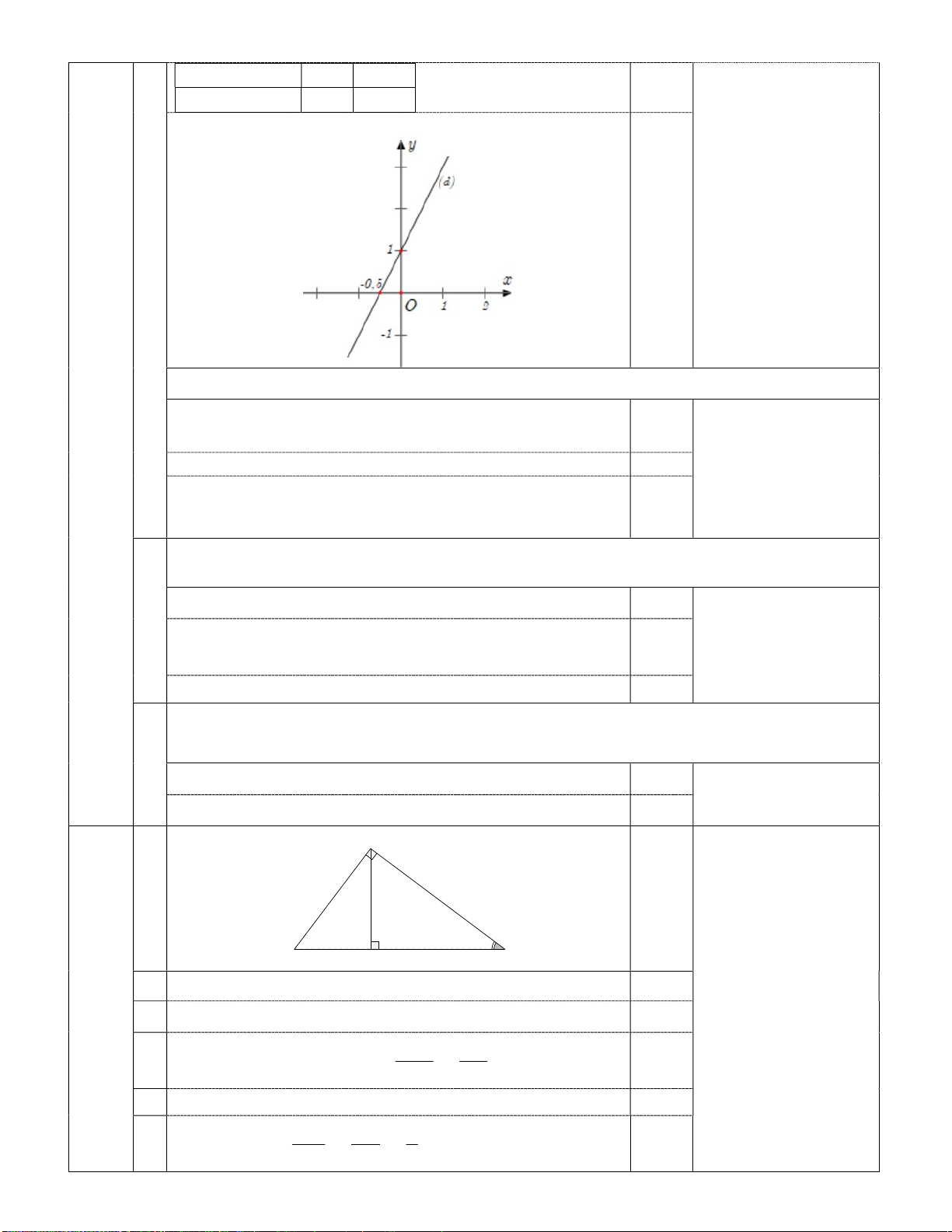
1 Vẽ (d) trên cùng mặt phẳng tọa độ Oxy. x 0  , 0 5 y  x 2 1 0,25 1 0
- Mặt phẳng tọa độ thiếu 1 trong các yếu tố mũi tên, O, x, y không trừ điểm.
- Nếu thiếu từ 2 yếu tố trở lên hoặc chia đơn vị
không đều trên 2 trục tọa 0,25
độ không chấm điểm đồ thị. - Ghi trục Ox thành trục
Oy và ngược lại thì không chấm đồ thị.
Tìm tọa độ giao điểm của (d) và (d ) bằng phép tính. III 1 (2,0đ)
PT hoành độ giao điểm của (d) và (d ): 1 0,25 x 2  1  x   7 HS không giải PT hoành  x 3  6
độ giao điểm mà chỉ ghi
 x  2  y  2  2  4
kq thì không chấm điểm.
Vậy tọa độ giao điểm của (d) và (d ) là  ;2 4. 0,25 1
Viết phương trình đường thẳng (d') : y  ax b biết (d') song song với (d) và cắt trục
tung tại điểm F có tung độ là 2.
Vì (d') song song với (d)  y  x 2 b, b (  1). 0,25 - Không ghi b  1 chấm 2 trọn điểm.
Vì (d') cắt trục tung tại điểm F có tung độ là 2
- Tìm được giá trị b mà
 b  2. (TMĐK b  1).
chưa kết luận pt đường thẳng thì không chấm. Vậy (d') : y  x 2 2. 0,25
Cho hai đường thẳng sau: (d ) : y  2x  2020 , (d ) : y  3x  1. Nêu vị trí tương đối của 2 3 (d) và (d ) ; (d) và (d ) 3 2 3 (d) // (d ). 0,25 2 Không ghi giải thích chấm trọn điểm. (d) cắt (d ). 0,25 3 A
- Vẽ được tam giác có kí 6cm 4,8cm 0,25 hiệu hai góc vuông đạt 0,25đ. B H C
- Không vẽ hình thì không IV 2 2 2 2 2 chấm bài làm. *BH  AB  AH  6  , 4 8  1 , 2 9 . 6 0,25 (1,5đ)  BH  , 3 6(cm). 0,25
- Có vẽ hình nhưng thiếu 1 góc vuông thì không 2 2 2 6 chấm điểm hình. * AB AB  BH.BC  BC    1 ( 0 cm). 0,25 BH , 3 6
- Thiếu đơn vị trừ 0,25đ HC  BC BH  10  , 3 6  , 6 ( 4 cm). 0,25 cả câu. 4 8 3 *  AH , tan ACH    . 0,25 CH , 6 4 4
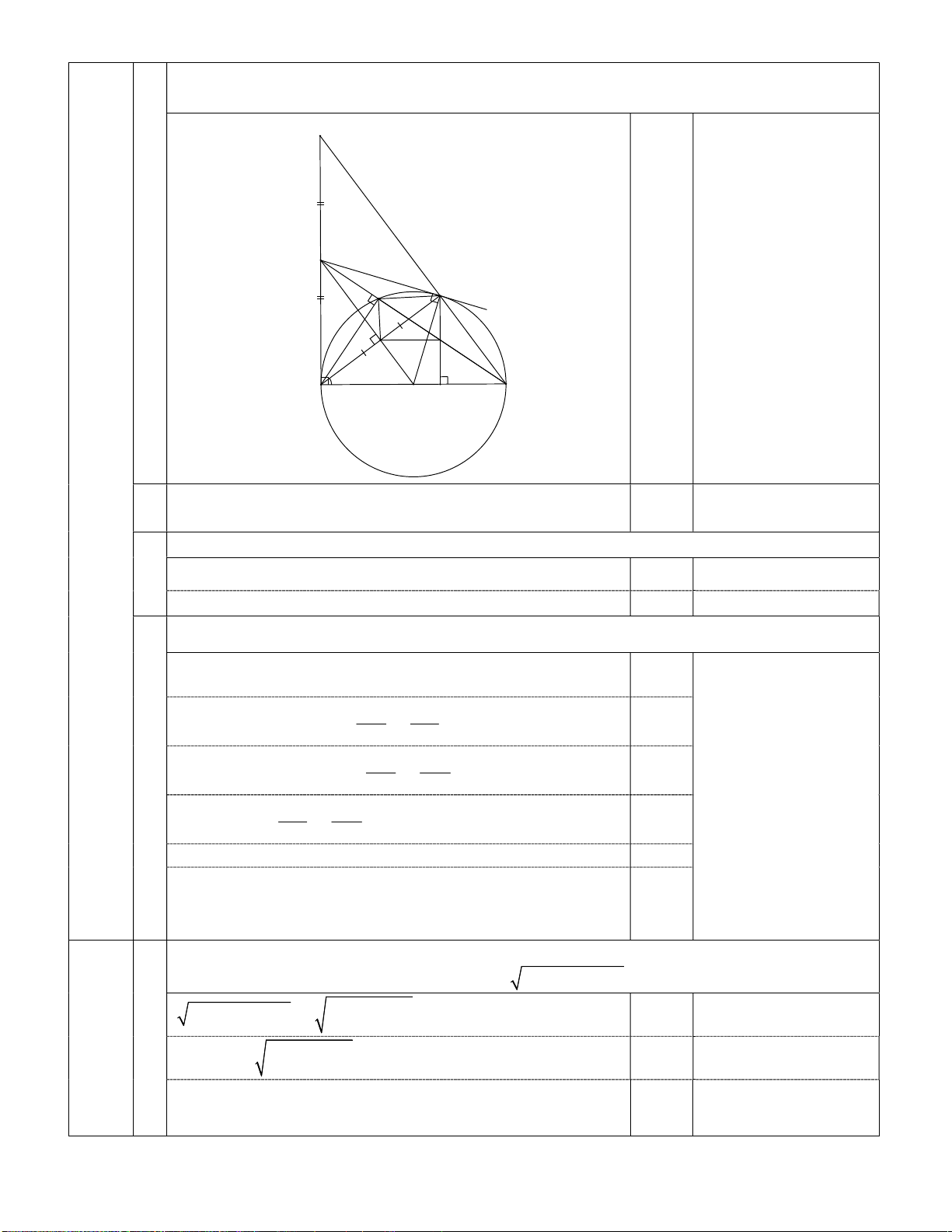
Cho đường tròn tâm O đường kính AB , C là điểm thuộc đường tròn ( AC  AB) . Tiếp
tuyến tại A của đường tròn (O) cắt BC tại D . Vẽ dây AE vuông góc với OD tại F . S - Hình vẽ đúng đường
tròn tâm O và tiếp tuyến đạt 0,25đ. D
- Thiếu kí hiệu góc vuông C E 0,25
tại tiếp điểm thì không chấm điểm hình. F H
- Không vẽ hình hoặc vẽ A B
hình sai không chấm điểm O K cả câu. Chứng minh AC  DB 0,25 a
và các điểm A,F,C,D cùng thuộc một đường tròn. 0,5 IV
Chứng minh DE là tiếp tuyến của đường tròn (O).
(2,5đ) b CM được DEO vuông tại E 0,25
 DE  EO tại E  (O). 0,25
Đường thẳng qua E vuông góc với AB tại K cắt BC tại H . Chứng minh HF //AB .
Gọi S là giao điểm của BE và AD . 0,25
Chứng minh được D là trung điểm của AS . SDB có BH HE HE//SD   - Phần chứng minh HS có BD DS
thể không ghi căn cứ kèm c có BH HK theo. ADB HK //AD   BD DA - Nếu HS trình bày cách Từ đó suy ra HE HK  0,25
giải khác đúng, lý luận DS DA chặt chẽ thì chấm theo
mà DS  DA suy ra HE  HK 0,25
biểu điểm tương đương. lại có FA  FE
do đóHF là đường trung bình của E  AK  HF//AK 0,25 hay HF//AB .
Tìm giá trị nhỏ nhất của biểu thức: P   x2 2020 1 x 0  26. x 1 x 0  26  x 52 2 0,5 VI  1  1, x   (1,0đ)   x  2 2020
5  1  2020  1  2021, x   0,25 Hay P  2021, x   x 
Vậy MinP  2021 khi x  5. 0,25 Không nêu khi 5 không chấm.
HEÁT 