Đề thi thử vào lớp 10 môn Toán 2017 – 2018 trường Archimedes Academy – Hà Nội lần 6

1/7 Nhóm Toán THCS Toán học là đam mê
THCS ARCHIMEDES ACADEMY
ĐỀ THI THỬ LẦN 06
Toán (Năm học 2017-2018)
Ngày thi: 21 – 4 – 2018
Thời gian: 120 phút.
Câu I. (2,0 điểm) Cho hai biểu thức x  7 x 2 x 1 2x  x  3 A  và B   
(với x  0, x  9 ) x x  3 x  3 x  9
1. Tính giá trị của biểu thức A khi x  16. 2. Rút gọn biểu thức B. 1
3. Tính giá trị nhỏ nhất của biểu thức P  A  . B
Câu II: (2,0 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một ô tô đi từ A đến B cách nhau 260km, sau khi ô tô đi được 120km với vận tốc dự định thì tăng
vận tốc thêm 10km/h trên quãng đường còn lại. Tính vận tốc dự định của ô tô, biết xe đến B sớm hơn
thời gian dự định 20 phút. Câu III:(2,0 điểm)
x  2 y  3
1. Cho hệ phương trình  ( m là tham số ). x  my  1 
Tìm giá trị nguyên của m để hệ có nghiệm duy nhất  x, y sao cho x, y là các số nguyên.
2. Cho parabol  P 2
: y  x và đường thẳng d  : y  2
 mx  4m ( m là tham số)
a) Tìm m để d  cắt  P tại hai điểm phân biệt , A B .
b) Giả sử x , x là hoành độ của ,
A B . Tìm m để x  x  3 . 1 2 1 2
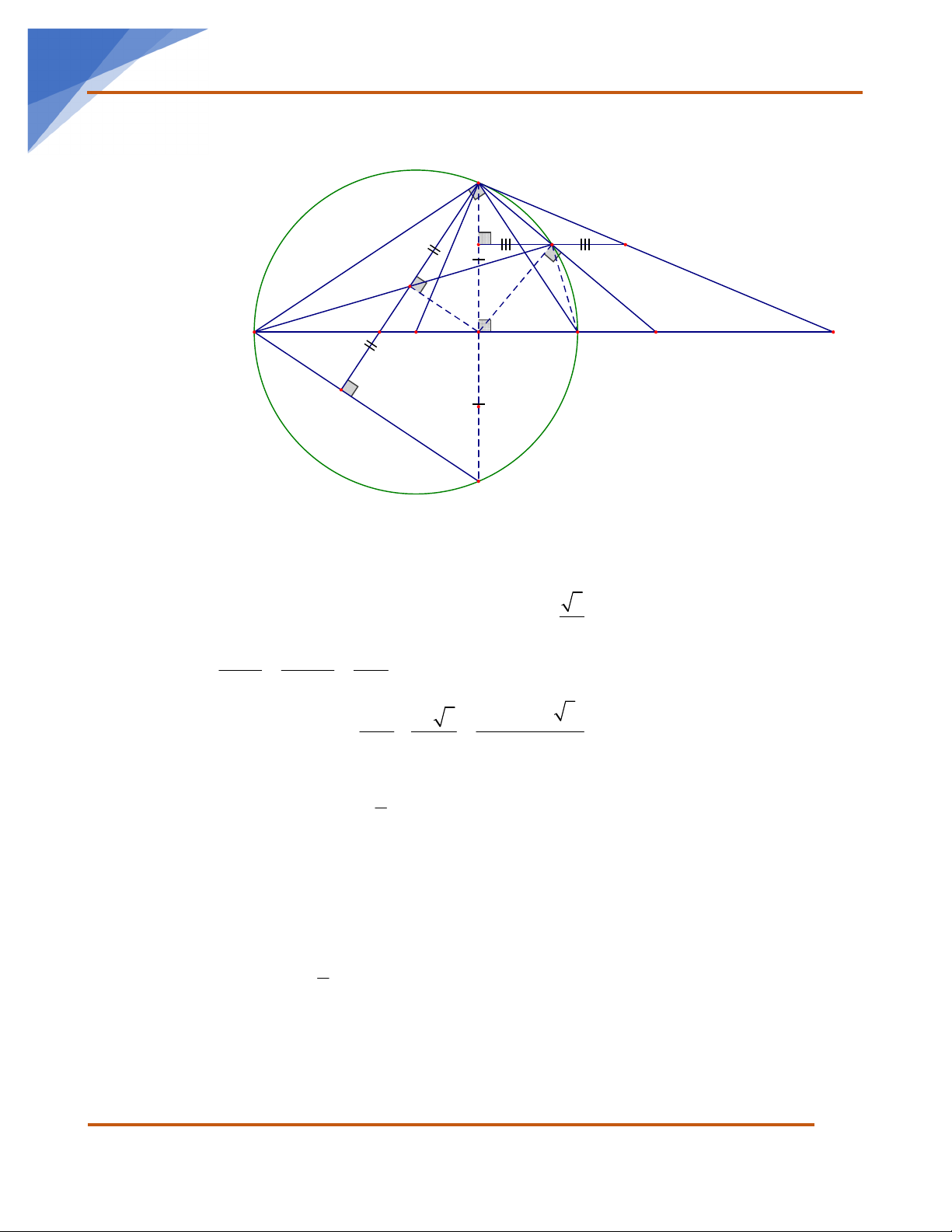
Câu IV: Cho tam giác ABC nội tiếp đường tròn  ;
O R , đường kính BC (AB > AC). Từ A kẻ tiếp
tuyến với đường tròn O cắt tia BC tại M . Kẻ dây AD vuông góc với BC tại H .
1) Chứng minh rằng: AMDO nội tiếp.  2) Gỉa sử 0
ABC  30 . Tính diện tích viên phân giới hạn bởi dây AC và cung AC nhỏ theo R .
3) Kẻ AN vuông góc với BD ( N thuộc BD ), gọi E là trung điểm của AN , F là giao điểm thứ
hai của BE với O , P là giao điểm của AN với BC , Q là giao điểm của AF với BC . Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 2/7 Nhóm Toán THCS Toán học là đam mê
a) Chứng minh tứ giác AEHF nội tiếp. b) Chứng minh 2 BH  B . P BQ .
4) Từ F kẻ đường thẳng song song với BC cắt AD và AM lần lượt tại I và K . Chứng minh
rằng F là trung điểm IK. 2 2 2
Câu V: (0,5 điểm) Cho các số thực a, b, c thỏa mãn a  ; 2 b  ;
5 c  5 và 2a  b  c  69 .
Tính GTNN của P  12a  b 13  c 11 . HƯỚNG DẪN GIẢI: Câu 1:
1. Thay x  16 (tmđk) vào biểu thức A ta có: 16  7 23 A   16 4 x 2 x 1 2x  x  3 2. B    x  3 x  3 x  9 x  x  3
2 x  1 x  3 2x  x  3 B   
 x  3 x  3  x  3 x  3  x  3 x  3 x  3 x 2x  5 x  3 2x  x  3 B   
 x  3 x  3  x  3 x  3  x  3 x  3 x x  x  x  3 3  B    x
 x  3 x  3  x  3 x  3
Vậy với x  0, x  9 thì B  x. 1 x  7 7 7
3. Với x  0, x  9 thì P  A    x  2 x   2 2 x.  2 14. B x x x 7 7
Dấu “ ” xảy ra khi và chỉ khi 2 x 
 2x  7  x  (tmđk) x 2 7
Vậy giá trị nhỏ nhất của P là 2 14 khi x  . 2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 3/7 Nhóm Toán THCS Toán học là đam mê Câu II:
Gọi vận tốc dự định của ô tô là x ( km/h, x  0 ) 260
Thời gian dự định đi hết quãng đường AB là (h) x 120
Thời gian thực tế ô tô đi trên quãng đường dài 120 km là (h) x 140
Thời gian thực tế ô tô đi trên quãng đường còn lại là (h) x 10 1
Vì xe đến B sớm hơn thời gian dự định 20 phút = h nên ta có phương trình 3 120 140 1 260    x x 10 3 x 2
 360x  3600  420x  x 10x  780x  7800 2
 x 10x  4200  0 x  70(  KTM)
 x  60(TM) 
Vậy vận tốc dự định của ô tô là 60 km/h. Câu III:
1. Hệ phương trình có nghiệm duy nhất khi m  2 .
x  3  2 y
x  3  2 y  x  3  2 y  HPT        . x  my  1 m   2 2 y  2  y      m  2 2 
Với y    x  3  2 y   . Vậy, để x, y là các số nguyên    . m  2
 m  2  ¦ 2  m  2   1;  
2  m  0;1;3;  4 . 2.
Xét phương trình hoành độ giao điểm của d  cắt  P Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 4/7 Nhóm Toán THCS Toán học là đam mê 2
x  2mx  4m  0 Có 2
 '  m  4m  m m  4 . a)
Để d  cắt  P tại hai điểm phân biệt , A B
  '  0  m m  4  0  m  4 hoặc m  0 . b)
x  x  2m; Theo hệ thức Vi-et có: 1 2  . x .x   4m 1 2
+) Xét m  4  x .x  4m  0 1 2 3
Do đó, x  x  3  x  x  3  2
 m  3  2m  3  m 
(loại, vì m  4 ). 1 2 1 2 2
+) Xét m  0  x .x  4m  0 1 2 2  ' Do đó, 2
x  x  3  x  x  3 
 3  2 m  4m  3 1 2 1 2 a 2
 4m 16m  9  0  9 m  lo¹i  2   1 m   nhËn  2 1 Vậy m   . 2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 5/7 Nhóm Toán THCS Toán học là đam mê Câu IV: A I F K E B C P O H Q M N D 
1) Dễ dàng chứng minh được 0
ODM  90  Tứ giác AODM nội tiếp (tổng hai góc đối bằng 0 180 ).  0  3 2) 0
ABC  30  ACB  60  A  OC đều 2  S  R . AO  C 4 2 2 2  R n  R 60  R S    quatAOC 360 360 6 2 2 2 R  R R 2 3 3 3   S  S  S    vpCFA quatAOC AO  C 6 4 12 3)   1 
a) Xét O có BAD  BFA  sd AB (góc nội tiếp). 2  
Mà EH là đường trung bình của A
 ND  EH / / ND  AHE  ADN (hai góc ở vị trí so le).  
AFE  AHE  AEHF nội tiếp (hai góc kề bằng nhau cùng chắn cung AE ) b) Ta có   
BEP  AEF (đối đỉnh)   1   AEF  AHF 
FA (tứ giác AEHF nội tiếp) 2   
AHF  AQH ( cùng phụ với  QHF ) Suy ra   BEP  BQF
Xét tam giác BPE và tam giác BFQ có Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 6/7 Nhóm Toán THCS Toán học là đam mê +  B chung +  
BEP  BQF (chứng minh trên) BP BE Suy ra B  PE ~ B  FQ    B .
P BQ  BE.BF   1 BF BQ BE BH
Chứng minh tương tự ta có 2 BE  H ~ BH  F  
 BH  BE.BF 2 BH BF Từ (1) và (2) suy ra 2 BH  B . P BQ    1   4)
Ta có: HAM  NBA  sđ D A    2  BN AN
Khi đó: HAM ~ NBA   AH HM Mặt khác:    1   EBN  HAQ  sđ AF    2  BN EN
Suy ra: EBN ~ QAH   AH QH AN EN 1 1 Khi đó: 
mà E là trung điểm AN  EN  AN  HQ 
HM  HQ  QM HM QH 2 2 IF FK Do IK / / HM  
 FI  FK  F là trung điểm IK HQ QM Câu 5: a  2  x  Đặt b
  5  y  x, y, z  0 c  5  z 
Khi đó từ giải thiết ta co : 2x2 + y2 +z2 + 8x + 10y + 10z = 11
Giả sử max {y,z} > 1. Do đó x, y, z ≥ 0  VT (*) > 11
Suy ra: 0  y, z  1
Mặt khác dễ thấy (*)  x  2 Khi đó ta có: 2 4x  2x  2 2 2 2 2 2 2 3  y  y
 4x  3y  z  2x  y  z  12x 13y 11z  2x  y  z  8x 10 y 10z  11  2 z  z  Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 7/7 Nhóm Toán THCS Toán học là đam mê
Suy ra P  12(x  2) 13( y  5) 11(z  5)  12x 13y 11z 144  11144  155 2 4x  2x x  0 a  2    Vậy P 2 min = 155  3  y  y
  y  0  b   5  2   z  z z  1 c  6   
Cám ơn các thầy cô: Thao Ngo (Câu 1) Van Anh Nguyen (Câu 2) Lương Pho (Câu 3) Hanh Nguyen (Câu 4) Nguyễn Văn Vui (Câu 5)
Đã nhiệt tình tham gia và hoàn thành dự án này !
Hi vọng tiếp tục được cộng tác với các thầy cô trong nhóm Toán THCS ở các dự án tiếp theo! Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/