Đề thi thử vào lớp 10 môn Toán năm 2021 – 2022 trường THCS Phù Linh – Hà Nội

TRƯỜNG TRUNG HỌC CƠ SỞ
KỲ THI THỬ VÀO LỚP 10 THPT PHÙ LINH
Năm học 2021 – 2022
Lần thi thử: 01; Môn thi: Toán 9; ĐỀ CHÍNH THỨC
Ngày thi: 22 tháng 05 năm 2021;
Thời gian làm bài: 120 phút.
Bài I (2,0 điểm): 2 1 x Cho biểu thức A = và B = −
(với x ≥ 0 và x ≠ 4) x + 2 x − 2 4 − x
1) Tính giá trị của biểu thức B tại x = 16. B
2) Rút gọn biểu thức P = . A
3) Tìm tất cả các giá trị nguyên của x để P < 1.
Bài II (2,5 điểm):
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một công ty vận tải dự định điều một số xe tải để vận chuyển 24 tấn hàng. Nhưng khi sắp khởi
hành thì công ty có 2 xe được điều đi làm việc khác nên mỗi xe còn lại phải chở thêm 2 tấn hàng so
với dự định. Hỏi số xe thực tế mà công ty điều động chở hàng là bao nhiêu?
2) Một đoạn ống nước hình trụ dài 5m, có dung tích 32m3. Tính diện tích đáy của ống nước đó.
Bài III (2,0 điểm):  (
2 x + y) + x +1 = 4
1) Giải hệ phương trình ( .
 x + y)− 3 x +1 = −5
2) Trong mặt phẳng tọa độ Oxy cho parabol (P): 2
y = −x và đường thẳng (d): y = mx − m − 2 (m là tham số). a) Với m = 2
− , tìm tọa độ giao điểm của đường thẳng (d) và parabol (P).
b) Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm biệt có hoành độ x x − x = 1, x2 thỏa mãn 20 . 1 2
Bài IV (3,0 điểm):
Cho tam giác ABC nhọn nội tiếp đường tròn (O; R). Ba đường cao AD, BE, CF của tam giác
ABC cùng đi qua trực tâm H. Kẻ đường kính AK của đường tròn (O; R). Gọi M là hình chiếu vuông
góc của C trên AK.
1) Chứng minh tứ giác BFEC nội tiếp được đường tròn.
2) Chứng minh AB. AC = 2R.AD và MD // BK.
3) Giả sử BC là dây cung cố định của đường tròn (O; R) và A di động trên cung lớn BC. Tìm
vị trí điểm A để diện tích tam giác AEH lớn nhất.
Bài V(0,5 điểm):
Cho hai số thực dương a, b thỏa mãn điều kiện a + b ≥ 3 . Tìm giá trị lớn nhất của biểu thức 1 2
M = a + b + + . 2a b
……………………Hết ……………………
TRƯỜNG TRUNG HỌC CƠ SỞ
ĐỀ THI THỬ VÀO LỚP 10 THPT PHÙ LINH
Năm học 2021 – 2022 Lần thi thử: 01; ĐỀ CHÍNH THỨC
Môn thi: Toán 9;
Ngày thi: 22 tháng 05 năm 2021;
Thời gian làm bài: 120 phút. Bài Ý Hướng dẫn chấm Điểm 2 1 x Cho biểu thức A = và B = −
(với x ≥ 0 và x ≠ 4) x + 2 x − 2 4 − x 0,5
Tính giá trị của biểu thức B tại x = 16.
Thay x = 16 (tmđk) vào biểu thức B, ta có: 1) 1 16 0,25 B = − 16 − 2 4 −16 5 Tính được B = . 0,25 6 B
Rút gọn biểu thức P =
( với x ≥ 0 và x ≠ 4) 1,0 A  1 x  2 P = − :   0,25 x − 2 4 − x x + 2    1 x  2 2 P = + : P = : Bài I   0,25 x − 2 
( x −2)( x +2) x +2  x + 2 (2,0 điểm) 2)  1 x  2 x + 2 + x 2 P = + =   0,25 x − 2 
( x −2)( x + ) : 2 x + 2 
( x −2)( x + ): 2 x + 2 2 x + 2 2 x +1 P = ( = x − 2)( x + ): 2 x + 2 x − 2 0,25 x +1 Vậy P =
với x ≥ 0 và x ≠ 4. x − 2
Tìm tất cả các giá trị nguyên của x để P < 1. 0,5 x +1 3 Ta có: P < 1 ⇔ <1 ⇔
< 0 (nhận xét: 3 > 0) x − 2 x − 2 3) 0,25
⇔ x − 2 < 0 ⇔ x < 4
Kết hợp với đkxđ, ta có 0 < x < 4 0,25
Mà x ∈ Z nên, suy ra x = 1 ; x = 2 ; x = 3
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một công ty vận tải dự định điều một số xe tải để vận chuyển 24 tấn hàng.
Nhưng khi sắp khởi hành thì công ty có 2 xe được điều đi làm việc khác 2,0 Bài II (2,5 điể 1)
nên mỗi xe còn lại phải chở thêm 2 tấn hàng so với dự định. Hỏi số xe m)
thực tế mà công ty điều động chở hàng là bao nhiêu?
Gọi số xe thực tế của công ty điều động chở hàng là x (xe; x ∈ N*) 0,5
Số xe dự định mà công ty dự điều chở hàng là x + 2 (xe) 24
Số tấn hàng mà thực tế mỗi xe phải chở là (tấn) x 0,5 24
Số tấn hàng mà dự định mà mỗi xe phải chở là (tấn) x + 2
Vì thực tế mỗi xe phải chở thêm 2 tấn hàng so với dự định nên, ta có phương trình: 24 24 0,5 − = 2 x x
Giải phương trình trên, ta được hai nghiệm x = 6
− (loại); x = 4 (tmđk) 0,5
Vậy số xe thực tế công ty điều động chở hàng là 4 xe.
Một đoạn ống nước hình trụ dài 5m, có dung tích 32m3. Tính diện tích đáy 0,5 của ống nước đó.
Vì ống nước hình trụ có h = 5m và dung tích V = 32m3 nên: 2) V 32 0,25 V = S h . ⇒ ông 2 S = = = , 6 m ông đay đay 4 h 5
Vậy diện tích đáy của ống nước đó là Sđáy = 6,4m2. 0,25  (
2 x + y) + x +1 = 4
Giải hệ phương trình ( . 0,75
 x + y)−3 x +1 = −5 2a + b = Đkxđ: 4 x ≥ 1
− . Đặt x + y = a và x +1 = b , hệ trở thành:  . 0,25
a − 3b = −5 1)
Giải hệ trên ta được a = 1; b = 2 0,25 x + y = 1 x = 3
Trở lại ẩn x, y ta có:  ⇔   x +1 = 2 y = −2 0,25
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = ( ; 3 2 − ).
Trong mặt phẳng tọa độ Oxy cho parabol (P): 2
y = −x và đường thẳng
(d): y = mx − m − 2 (m là tham số). Với m = 2
− , tìm tọa độ giao điểm của 0,5
đường thẳng (d) và parabol (P). Bài III
Xét phương trình hoàn độ giao điểm của (P) và (d) khi m = 2 − : 2a) (2,0 điểm) x = 0 0,25 2 − x = 2 − x − ( 2 − ) − 2 ⇔ 2
x − 2x = 0 ⇔ x(x − 2) = 0 ⇔  x = 2
Với x = 0 ⇒ y = 02 = 0; x = 2 ⇒ y = –22 = –4 0,25 Vậy khi m = 2
− thì tọa độ giao điểm của (d) và (P) là ( 0 ; 0 ) và ( ; 2 4 − ).
Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm 0,75
biệt có hoành độ x x − x = 1, x2 thỏa mãn 20 . 1 2
Xét phương trình hoành độ giao điểm của (P) và (d), ta có: 2
x + mx − m − 2 = 0 (1) 2b) Ta có: 2
∆ = m − 4(−m − 2) = (m + 2)2 + 4 . 0,25
Nhận xét ∆ = (m + 2)2 + 4 > 0 với ∀m, suy ra phương trình (1) luôn có hai
nghiệm; do đó (d) luông cắt (P) tại hai điểm phân biệt.
x + x = −m
Theo hệ thức, Viét, ta có:  1 2 . 0,25
x .x = −m − 2 1 2
Theo đề bài, ta có: x − x = 20 ⇔ (x + x − x x = (2) 1 2 )2 4 20 1 2 1 2
Thay x + x = −m và x .x = −m − 2 vào (2), ta có: 1 2 1 2 (− m)2 − (
4 − m − 2) = 20 ⇔ 2
m + 4m −12 = 0 m = −6 0,25
⇔ (m + 6)(m − 2) = 0 ⇔  . m = 2 Vậy m = 6
− ; m = 2 là các giá trị cần tìm.
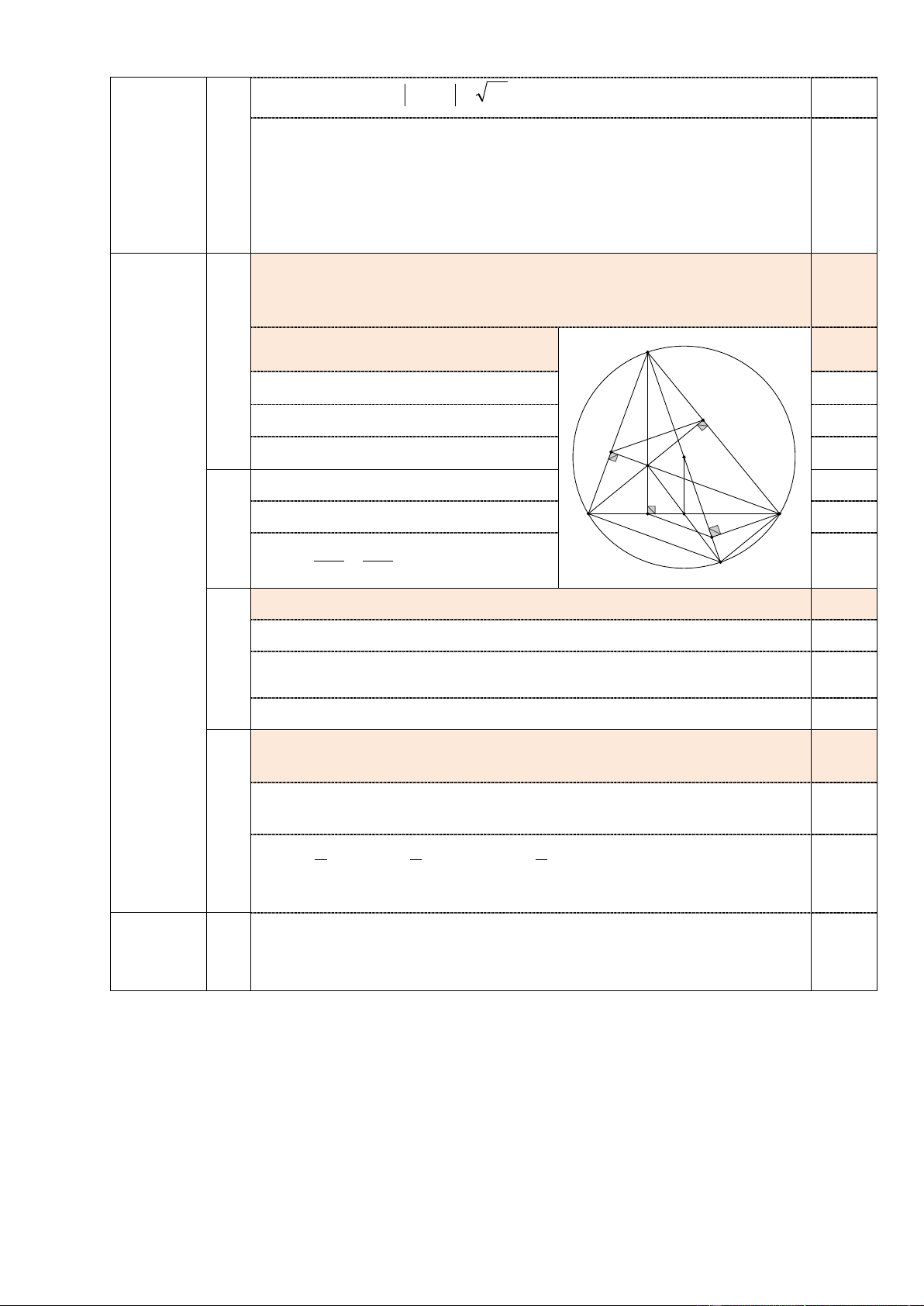
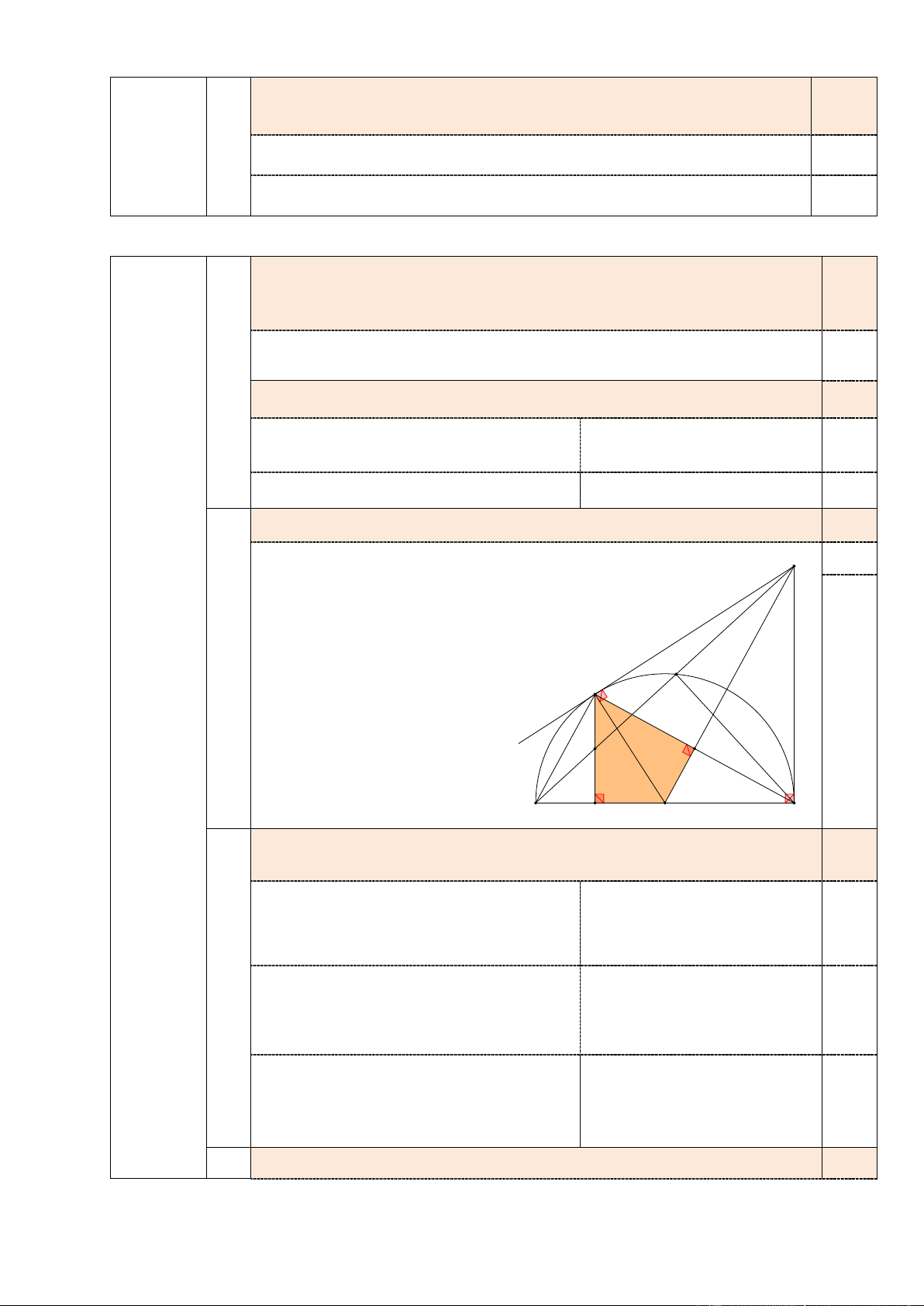
Cho tam giác ABC nhọn nội tiếp đường tròn (O; R). Ba đường cao AD,
BE, CF của tam giác ABC cùng đi qua trực tâm H. Kẻ đường kính AK của
đường tròn (O; R). Gọi M là hình chiếu vuông góc của C trên AK.
Chứng minh tứ giác BFEC nội tiếp A 1,0 1) được đường tròn.
Vẽ hình đúng đến ý 1) 0,25
Chứng minh được 𝐵𝐵𝐵𝐵𝐵𝐵 � = 𝐵𝐵𝐵𝐵𝐵𝐵 � = 900 E 0,25
Xét tứ giác BFEC ⇒ nội tiếp F O 0,5 H
Chứng minh AB. AC = 2R.AD: 0,5 D G
Chứng minh được ∆ABD ∽ ∆AKC 0,25 2a) B C AB AK M Suy ra =
⇒ AB. AC = 2R.AD 0,25 Bài IV AD AC K (3,0 điểm)
Chứng minh MD // BK: 0,75
Chứng minh ◊ADMC nội tiếp 0,25
2b) Suy ra 𝐵𝐵𝐶𝐶𝐶𝐶 � = 𝐵𝐵𝐶𝐶𝐶𝐶 � (1) 0,25
Chứng minh 𝐵𝐵𝐵𝐵𝐶𝐶 � = 𝐵𝐵𝐶𝐶𝐶𝐶 � (2)
Từ (1), (2) ⇒ 𝐵𝐵𝐶𝐶𝐶𝐶 � = 𝐵𝐵𝐶𝐶𝐶𝐶
� ⇒ MD // BK. 0,25
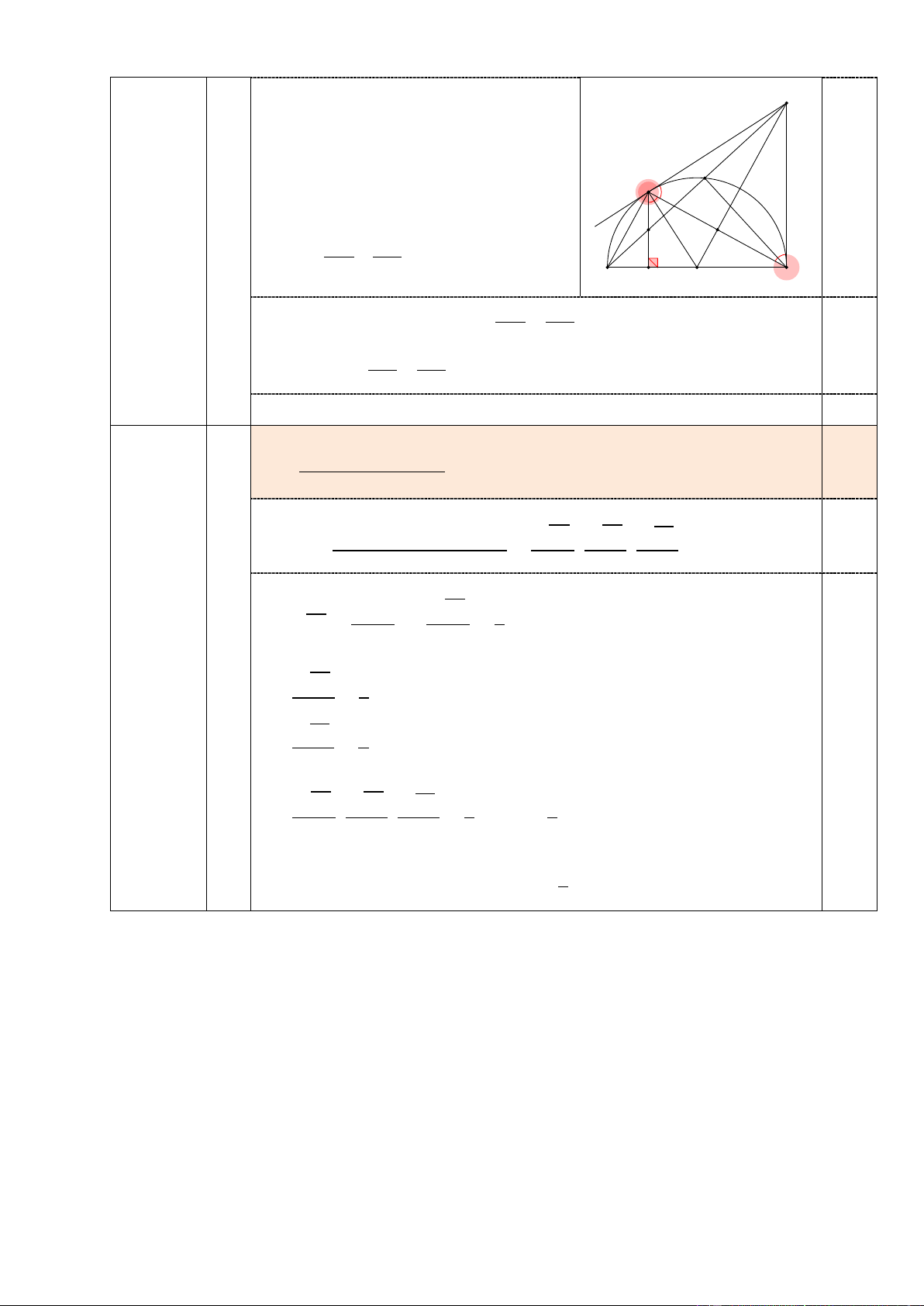
Giả sử BC là dây cung cố định của đường tròn (O; R) và A di động trên 0,75
cung lớn BC. Tìm vị trí điểm A để diện tích tam giác AEH lớn nhất.
Gọi G là giao điểm của BC và HK. 0,25 3)
Chứng minh được AH = 2.OG ⇒ AH không đổi 1 1 1 SAEH = AE. EH ≤ (AE2 + EH2) ≤ AH2 (ĐL Pytago) 2 4 4 0,25
Đẳng thức xảy ra ⇔ AE = EH
Suy ra ∆AEH vuông cân tại E ⇒ 𝐻𝐻𝐶𝐶𝐵𝐵
� = 450 ⇒ 𝐵𝐵𝐵𝐵𝐶𝐶 � = 450
Vậy để diện tích tam giác AEH lớn nhất thì điểm A thuộc đường tròn 0,25
(O; R) sao cho 𝐵𝐵𝐵𝐵𝐶𝐶 � = 450.
Cho hai số thực dương a, b thỏa mãn điều kiện a + b ≥ 3 . Tìm giá trị lớn 1 2 0,5
nhất của biểu thức M = a + b + + . 2a b
Biến đổi biểu thức M, ta có: 1 2  1 a   2 b  a + b
M = a + b + + =  +  +  +  + 2a b
 2a 2   b 2  2
Áp dụng BĐT Cô-si cho các cặp số dương, ta có: 1 a 1 a + ≥ 2 . =1 (1) 0,25 2a 2 2a 2 2 b 2 b + ≥ 2 . = 2 (2) Bài V b 2 b 2 (0,5 điểm) Theo đề a + b 3
, ta có: a + b ≥ 3 ⇒ ≥ (3) 2 2
Cộng vế với vế của (1), (2), (3), ta được:  1 a   2 b  a + b 9 9  +  +  +  + ≥ ⇒ M ≥
 2a 2   b 2  2 2 2
Đẳng thức xảy ra khi a, b dương và:   1 = a 2 b 0,25 ; =  2 a = ; 1 2 b = 4
2a 2 b 2 ⇔ 
⇔ a = 1 và b = 2 (tmđk)  a + b = 6   a + b = 3 9
Vậy giá trị lớn nhất của biểu thức M là
khi a = 1 và b = 2. 2
Chú ý chung khi chấm:
1) Điểm toàn bài để lẻ đến 0,25;
2) Các cách làm khác nếu đúng vẫn cho điểm tối đa;
3) Bài IV: Học sinh vẽ sai hình trong phạm vi câu nào thì không tính điểm câu đó. Nguồn đề
BGH TRƯỜNG THCS PHÙ LINH
TRƯỜNG TRUNG HỌC CƠ SỞ
KÌ THI THỬ VÀO LỚP 10 THPT PHÙ LINH
Năm học 2021 – 2022 Lần thi thử: 02; ĐỀ CHÍNH THỨC
Môn thi: Toán 9;
Ngày thi: 30 tháng 5 năm 2021;
Thời gian làm bài: 120 phút.
Bài I (2,0 điểm): x 3 6 x − 4 Cho biểu thức A = và B = −
(với x ≥ 0 và x ≠ 1) x − 1 x +1 x −1
1) Tính giá trị của biểu thức A khi x = 16.
2) Rút gọn biểu thức M = A + B. 1
3) Tìm x thuộc N* để nhận giá trị nguyên. M
Bài II (2,5 điểm):
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một xưởng cơ khí phải làm 350 chi tiết máy trong một thời gian quy định. Nhờ tăng năng suất
lao động, mỗi ngày xưởng làm thêm được 5 chi tiết máy so với quy định. Vì vậy chẳng những đã
làm vượt mức quy định 10 chi tiết máy mà còn hoàn thành sớm hơn quy định 1 ngày. Tính số chi tiết
máy mà xưởng phải làm trong một ngày theo quy định.
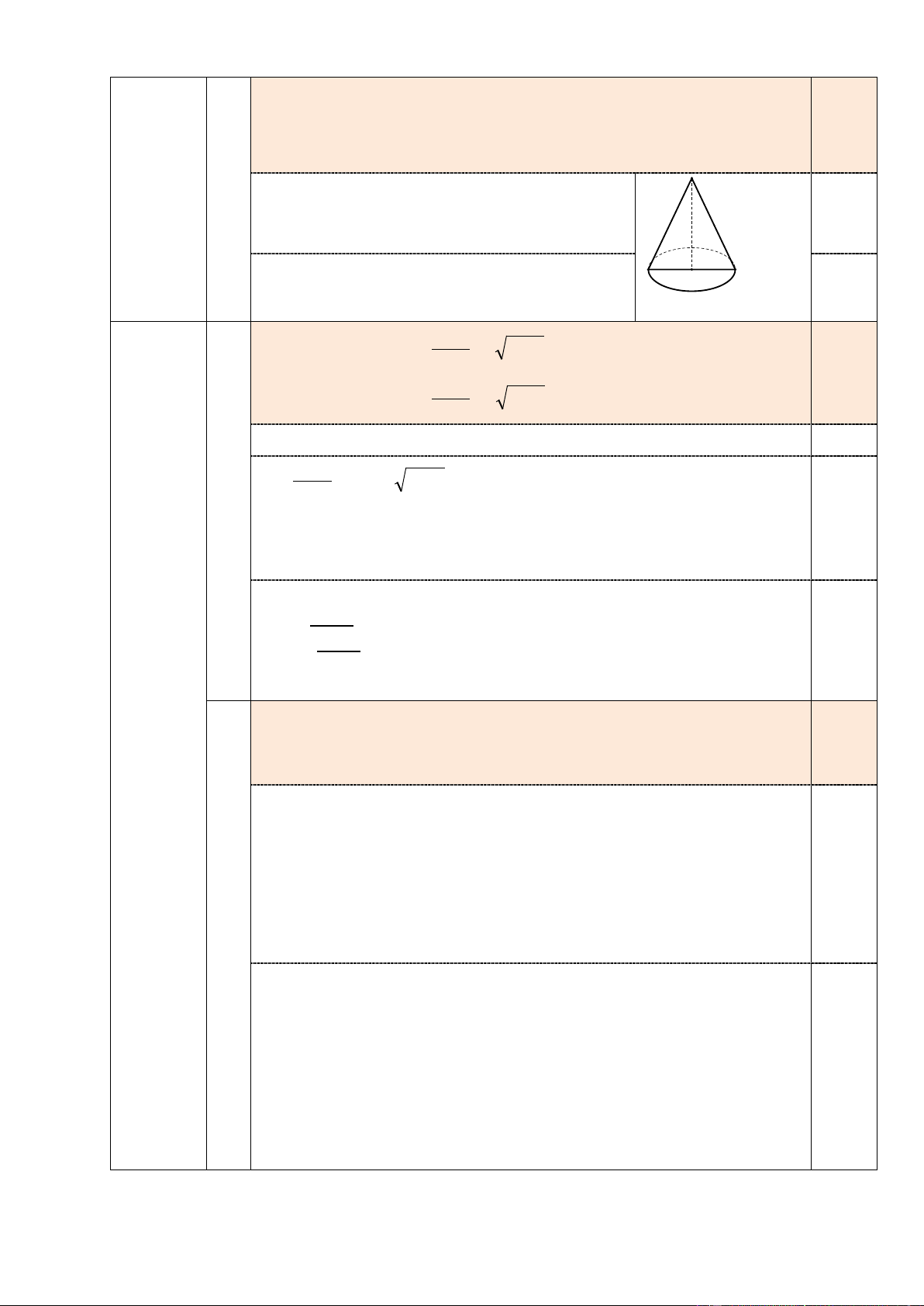
2) Chiếc nón do làng Chuông (Thanh Oanh – Hà Nội) sản xuất là hình nón có đường sinh bằng
30cm, đường kính đáy bằng 40cm. Người ta dùng hai lớp lá để phủ lên bề mặt xung quanh của nón.
Tính diện tích lá cần dùng cho một chiếc nón.
Bài III (2,0 điểm):  1 +3 y +3 =  7 x − 2
1) Giải hệ phương trình  .  3  − 2 y + 3 = −1  x − 2
2) Trong mp tọa độ Oxy cho parabol (P): 2
y = x và đường thẳng (d): y = ( 2 m + )
1 x − 2m −10 (m là tham số).
a) Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt.
b) Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x1, x2 sao cho biểu thức 2 2
A = 12x x + x + x đạt giá trị nhỏ nhất. 1 2 1 2
Bài IV (3,0 điểm):
Cho nửa đường tròn (O) đường kính AB. Trên nửa đường tròn (O) lấy điểm C sao cho
AC < BC (C khác A). Các tiếp tuyến tại B và C của (O) cắt nhau ở D, AD cắt (O) tại điểm E (E khác A).
1) Chứng minh rằng tứ giác BDCO nội tiếp đường tròn và BE2 = AE. DE.
2) Qua C kẻ đường thẳng song song với BD cắt AB tại H, DO cắt BC tại F. Chứng minh rằng
tứ giác CHOF nội tiếp đường tròn.
3) Gọi I là giao điểm của AD và CH. Chứng minh rằng I là trung điểm của CH.
Bài V(0,5 điểm): xyz
Cho x, y, z là ba số thực dương. Tìm giá trị lớn nhất của biểu thức M = ( .
x + y)(y + z)(z + x)
……………………Hết ……………………
TRƯỜNG TRUNG HỌC CƠ SỞ
KÌ THI THỬ VÀO LỚP 10 THPT PHÙ LINH
Năm học 2021 – 2022 Lần thi thử: 02; ĐỀ CHÍNH THỨC
Môn thi: Toán 9;
Ngày thi: 30 tháng 5 năm 2021;
Thời gian làm bài: 120 phút. Bài Ý Hướng dẫn chấm Điểm x 3 6 x − 4 Cho biểu thức A = và B = −
(với x ≥ 0 và x ≠ 1) x − 1 x +1 x −1 0,5
Tính giá trị của biểu thức A khi x = 16. Thay x = 16 (tmđk) vào biể 1) u thức A, ta có: √𝑥𝑥 √16 4 4 0,25 𝐴𝐴 = = =
√𝑥𝑥 − 1 √16 − 1 4 − 1 = 3 4 Vậy khi x = 16 thì . 0,25 3
Rút gọn biểu thức M = A + B (với x ≥ 0 và x ≠ 1) 1,0
Với x ≥ 0 và x ≠ 1, ta có: √𝑥𝑥 3 6√𝑥𝑥 − 4 𝑀𝑀 = + −
√𝑥𝑥 − 1 √𝑥𝑥 + 1 𝑥𝑥 − 1 0,25 √𝑥𝑥 3 6√𝑥𝑥 − 4 𝑀𝑀 = + −
√𝑥𝑥 − 1�√𝑥𝑥+1� √𝑥𝑥 + 1�√𝑥𝑥−1� �√𝑥𝑥 − 1��√𝑥𝑥 + 1� Bài I (2,0 điểm)
√𝑥𝑥�√𝑥𝑥 + 1� + 3�√𝑥𝑥 − 1� − �6√𝑥𝑥 − 4� 2) 𝑀𝑀 = 0,25
�√𝑥𝑥 − 1��√𝑥𝑥 + 1�
𝑥𝑥 + √𝑥𝑥 + 3√𝑥𝑥 − 3 − 6√𝑥𝑥 + 4 𝑥𝑥 − 2√𝑥𝑥 + 1 𝑀𝑀 = = 0,25
�√𝑥𝑥 − 1��√𝑥𝑥 + 1�
�√𝑥𝑥 − 1��√𝑥𝑥 + 1� �√𝑥𝑥 − 1�2 √𝑥𝑥 − 1 𝑀𝑀 = =
�√𝑥𝑥 − 1��√𝑥𝑥 + 1� √𝑥𝑥 + 1 0,25 x −1 Vậy M = . x +1 1
Tìm x thuộc N* để nhận giá trị nguyên. 0,5 M 1 x +1 2 3) Ta có: = =1+ . M x −1 x −1 0,25 Để 1 2
nhận giá trị nguyên thì
phải nguyên ⇔ x −1 ∈ Ư(2) M x − 2 ⎡√𝑥𝑥 − 1 = −2
⎡√𝑥𝑥 = −1 (vô nghiệm) 𝑥𝑥 = 0 (loại) ⎢√𝑥𝑥 − 1 = −1 ⎢√𝑥𝑥 = 0 ⇔ ⎢ ⇔ ⎢ ⇔ �𝑥𝑥 = 4 (tmđk) ⎢ √𝑥𝑥 − 1 = 1 ⎢√𝑥𝑥 = 2 𝑥𝑥 = 9 (tmđk) 0,25 ⎣ √𝑥𝑥 − 1 = 2 ⎣√𝑥𝑥 = 3
Kết luận: x = 4; x = 9 là các giá trị cần tìm.
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một xưởng cơ khí phải làm 350 chi tiết máy trong một thời gian quy
định. Nhờ tăng năng suất lao động, mỗi ngày xưởng làm thêm được 5 chi 2,0
tiết máy so với quy định. Vì vậy chẳng những xưởng đã làm vượt mức
quy định 10 chi tiết máy mà còn hoàn thành sớm hơn quy định 1 ngày.
Tính số chi tiết máy mà xưởng phải làm trong một ngày theo quy định
Gọi số chi tiết máy mà xưởng phải làm trong một ngày theo quy định là x (chi tiết; x ∈ N*) 0,25
(Gọi số chi tiết máy theo quy định mà xưởng phải làm trong một ngày là x)
(Theo quy định, gọi số chi tiết máy mà xưởng phải làm trong một ngày là x)
(Gọi số chi tiết máy trong một ngày mà xưởng phải làm theo quy định là x)
Trên thực tế, một ngày xưởng làm được số chi tiết máy là x + 5 (chi tiết)
(Trên thực tế, số chi tiết máy xưởng làm được trong một ngày là x + 5) 0,25
(Số chi tiết máy xưởng làm được trong một ngày trên thực tế là x + 5) Theo quy định, xưở 350
ng làm 350 chi tiết máy hết thời gian là (ngày) x 360 0,5
Trên thực tế, xưởng làm 350 + 10 = 360 chi tiết máy hết thời gian là x + 5 Bài II (ngày) (2,5 điể 1) m)
Vì xưởng hoàn thành công việc sớm hơn một ngày so với quy định nên, ta có phương trình: 350 360 0,5 𝑥𝑥 − 𝑥𝑥 + 5 = 1
350(𝑥𝑥 + 5) − 360𝑥𝑥 ⟺ 𝑥𝑥(𝑥𝑥 + 5) = 1
350𝑥𝑥 + 1750 − 360𝑥𝑥 −10𝑥𝑥 + 1750 1 ⟺ 𝑥𝑥2 + 5𝑥𝑥 = 1 ⟺ 𝑥𝑥2 + 5𝑥𝑥 = 1 0,5
⟺ 𝑥𝑥2 + 5𝑥𝑥 = −10𝑥𝑥 + 1750 ⟺ 𝑥𝑥2 + 15𝑥𝑥 − 1750 = 0
⟺ (𝑥𝑥 − 35)(𝑥𝑥 + 50) = 0 ⟺ �𝑥𝑥 = 35 (tmđk) 𝑥𝑥 = −50 (loại)
Vậy số chi tiết máy mà xưởng phải làm một ngày theo quy định là x = 35 chi tiết. 0,25
Chiếc nón do làng Chuông (Thanh Oanh – Hà Nội) sản xuất là hình nón
có đường sinh bằng 30cm, đường kính đáy bằng 40cm. Người ta dùng hai 0,5
lớp lá để phủ lên bề mặt xung quanh của nón. Tính diện tích lá cần dùng cho một chiếc nón. 2)
Vì chiếc nón hình nón có đường sinh l = 30cm và
bán kính đáy R = 40 : 2 = 20cm nên: 0,25 S h l
xq = πRl = π . 20. 30 = 600π (cm2)
Vậy diện tích là cần dùng cho một chiếc nón là R 2 0,25 . 600π = 1200π cm2.
𝑺𝑺𝐱𝐱𝐱𝐱 = 𝝅𝝅𝝅𝝅𝝅𝝅  1 +3 y +3 =  7 x − 2
Giải hệ phương trình  . 1,0  3  − 2 y + 3 = −1  x − 2
Đkxđ: 𝑥𝑥 ≠ 2 và 𝑦𝑦 ≥ −3 0,25 Đặ 1 t
= a và y + 3 = b , hệ trở thành: x − 2 1) � 𝑎𝑎 + 3𝑏𝑏 = 7 0,5
3𝑎𝑎 − 2𝑏𝑏 = −1 ⟺ �3𝑎𝑎 + 9𝑏𝑏 = 21
3𝑎𝑎 − 2𝑏𝑏 = −1 ⟺ �𝑎𝑎 + 3𝑏𝑏 = 7 11𝑏𝑏 = 22 ⟺ �𝑎𝑎 + 6 = 7
𝑏𝑏 = 2 ⟺ �𝑎𝑎 = 1 𝑏𝑏 = 2
Trở lại ẩn x và y, ta có: 1
� 𝑥𝑥 − 2 = 1 ⟺ �𝑥𝑥 − 2 = 1
𝑦𝑦 + 3 = 4 ⟺ �𝑥𝑥 = 3 (tmđk) 𝑦𝑦 = 1 (tmđk) 0,25 �𝑦𝑦 + 3 = 2
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = ( )1 ; 3
Trong mp tọa độ Oxy cho parabol (P): 2
y = x và đường thẳng (d): Bài III y = ( 2 m + )
1 x − 2m −10 (m là tham số). 0,5 (2,0 điểm)
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt.
Xét phương trình hoành độ giao điểm của (P) và (d), ta có:
𝑥𝑥2 = 2(𝑚𝑚 + 1)𝑥𝑥 − 2𝑚𝑚 − 10
⇔ 𝑥𝑥2 − 2(𝑚𝑚 + 1)𝑥𝑥 + 2𝑚𝑚 + 10 = 0 (1)
Ta có: ∆′= 𝑏𝑏′2 − 𝑎𝑎𝑎𝑎 0,25
= [−(𝑚𝑚 + 1)]2 − 1. (2𝑚𝑚 + 10)
= 𝑚𝑚2 + 2𝑚𝑚 + 1 − 2𝑚𝑚 − 10 2a) = 𝑚𝑚2 − 9
Để (P) và (d) cắt nhau tại 2 điểm phân biệt ⇔ phương trình (1) có 2
nghiệm phân biêt ⇔ ∆′ > 0
⇔ 𝑚𝑚2 − 9 > 0 ⇔ (𝑚𝑚 − 3)(𝑚𝑚 + 3) > 0 ⎡�𝑚𝑚 − 3 > 0 ⎡� 𝑚𝑚 > 3 0,25 ⎢ 𝑚𝑚 + 3 > 0 ⎢ 𝑚𝑚 > −3 ⇔ ⎢ ⇔ ⎢ ⟺ � 𝑚𝑚 > 3 ⎢ ⎢ 𝑚𝑚 < −3 ⎣�𝑚𝑚 − 3 < 0 𝑚𝑚 + 3 < 0 ⎣� 𝑚𝑚 < 3 𝑚𝑚 < −3
Vậy 𝑚𝑚 < −3 hoặc 𝑚𝑚 > 3 là các giá trị cần tìm.
Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ x1, x2 sao 5 cho biểu thức 2 2
A = 12x x + x + x đạt giá trị nhỏ nhất. 1 2 1 2 2b) 0,25 0,25
Cho nửa đường tròn (O) đường kính AB. Trên nửa đường tròn (O) lấy điểm
C sao cho AC < BC (C khác A). Các tiếp tuyến tại B và C của (O) cắt nhau
ở D, AD cắt (O) tại điểm E (E khác A).
Vẽ đúng hình đến ý 1a) 0,25
1a) Chứng minh rằng tứ giác BDCO nội tiếp đường tròn 0,5
(Nếu một đường thẳng là tiếp tuyến
của đường tròn thì nó vuông góc với 0,25 bán kính)
(Tứ giác có tổng hai góc đối nhau
bằng 1800 là tứ giác nội tiếp) 0,25
Chứng minh BE2 = AE. DE 0,5 D 0,25 1b) E C Bài IV 0,25 (3,0 điểm) F A H O B
Qua C kẻ đường thẳng song song với BD cắt AB tại H, DO cắt BC tại F. 1,0
Chứng minh rằng tứ giác CHOF nội tiếp đường tròn.
(Nếu một đường thẳng vuông góc Ta có: CH // BD (gt)
với một trong hai đường thẳng song AB ⊥ BD (cm ý 1a)
song thì nó vuông góc với đường 0,25 thẳng còn lại)
⇒ AB ⊥ CH ⇒ 𝐶𝐶𝐶𝐶𝐶𝐶 � = 900
Xét (O): DC = DB (t/c hai tiếp tuyến x)
(Những điểm cách đều hai đầu 2) OC = OB (=R)
đoạn thẳng thì nằm trên đường
trung trực của đoạn thẳng ấy) 0,25
⇒ DO là trung trực của CB
⇒ DO ⊥ CB ⇒ 𝐶𝐶𝐶𝐶𝐶𝐶 � = 90 Xét ◊CHOF, ta có:
(Tứ giác có tổng hai góc đối nhau 𝐶𝐶𝐶𝐶𝐶𝐶 � + 𝐶𝐶𝐶𝐶𝐶𝐶
� = 900 + 900 = 1800 bằng 1800 là tứ giác nội tiếp) 0,5 𝐶𝐶𝐶𝐶𝐶𝐶 �, 𝐶𝐶𝐶𝐶𝐶𝐶 � là 2 góc đối nhau Suy ra ◊CHOF nội (đpcm).
Gọi I là giao điểm của AD và CH. Chứng minh I là trung điểm của CH. 0,75 D
Ta có: CH // BD (gt) ⇒ 𝐶𝐶1 � = 𝐵𝐵1 � (slt) (1)
Vì DC = DB nên ∆DCB cân tại D, suy ra: 𝐶𝐶2 � = 𝐵𝐵1 � (tính chất) (2) Từ (1), (2) ⇒ 𝐶𝐶 E 1 � = 𝐶𝐶2
� ⇒ CB là p/g 𝐶𝐶𝐶𝐶𝐶𝐶 � C 2 0,25
Xét (O): 𝐴𝐴𝐶𝐶𝐵𝐵
� = 900 ⇒ AC ⊥ CB 1
⇒ CA là p/ ngoài tại C của ∆ICD I F 3) AI CI ⇒ = (3) 1 AD CD A H O B AI HI
Xét ∆ABD có HI // BD, suy ra: = (4) AD BD 0,25 CI HI Từ (3), (4) ⇒ = CD BD
Mà CD = BD nên, suy ra CI = IH. Do đó I là trung điểm của CH 0,25
Cho x, y, z là ba số thực dương. Tìm giá trị lớn nhất của biểu thức xyz M = ( . 0,5
x + y)(y + z)(z + x)
Biến đổi biểu thức M, ta có: 𝑥𝑥𝑦𝑦𝑥𝑥
�𝑥𝑥𝑦𝑦 �𝑦𝑦𝑥𝑥 √𝑥𝑥𝑥𝑥 0,25
𝑀𝑀 = (𝑥𝑥 + 𝑦𝑦)(𝑦𝑦 + 𝑥𝑥)(𝑥𝑥 + 𝑥𝑥) = 𝑥𝑥 + 𝑦𝑦.𝑦𝑦 + 𝑥𝑥.𝑥𝑥 + 𝑥𝑥
Áp dụng bất đẳng thức Cô-si cho hai số dương, ta có: 𝑥𝑥 + 𝑦𝑦 �𝑥𝑥𝑦𝑦 1
�𝑥𝑥𝑦𝑦 ≤ 2 ⟹ 𝑥𝑥 + 𝑦𝑦 ≤ 2 (2) Bài V Tương tự, ta có: (0,5 điểm) �𝑦𝑦𝑥𝑥 1 𝑦𝑦 + 𝑥𝑥 ≤ 2 (2) √𝑥𝑥𝑥𝑥 1 0,25 𝑥𝑥 + 𝑥𝑥 ≤ 2 (3)
Nhân vế với vế của (1), (2) và (3), ta được:
�𝑥𝑥𝑦𝑦 �𝑦𝑦𝑥𝑥 √𝑥𝑥𝑥𝑥 1 1
𝑥𝑥 + 𝑦𝑦 . 𝑦𝑦 + 𝑥𝑥 . 𝑥𝑥 + 𝑥𝑥 ≤ 8 ⟹ 𝑀𝑀 ≤ 8
Đẳng thức xảy ra ⇔ x = y = z. 1
Vậy giá trị nhỏ nhất của biểu thức M là khi x = y = z. 8
Chú ý chung khi chấm:
1) Điểm toàn bài để lẻ đến 0,25;
2) Các cách làm khác nếu đúng vẫn cho điểm tối đa;
3) Bài IV: Học sinh vẽ sai hình trong phạm vi câu nào thì không tính điểm câu đó. Nguồn đề
BGH TRƯỜNG THCS PHÙ LINH
Document Outline

• Đáp án đề thi thử vào 10 Trường THCS Phù Linh ngày 22 tháng 5 năm 2021
• Đáp án đề thi thử vào 10 Trường THCS Phù Linh ngày 30 tháng 5 năm 2021