Đề thi thử vào lớp 10 môn Toán năm 2022 trường THCS Phúc Diễn – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi thử vào lớp 10 môn Toán năm 2022 trường THCS Phúc Diễn, quận Bắc Từ Liêm, thành phố Hà Nội; kỳ thi được diễn ra vào ngày 04 tháng 06 năm 2022; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm. Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
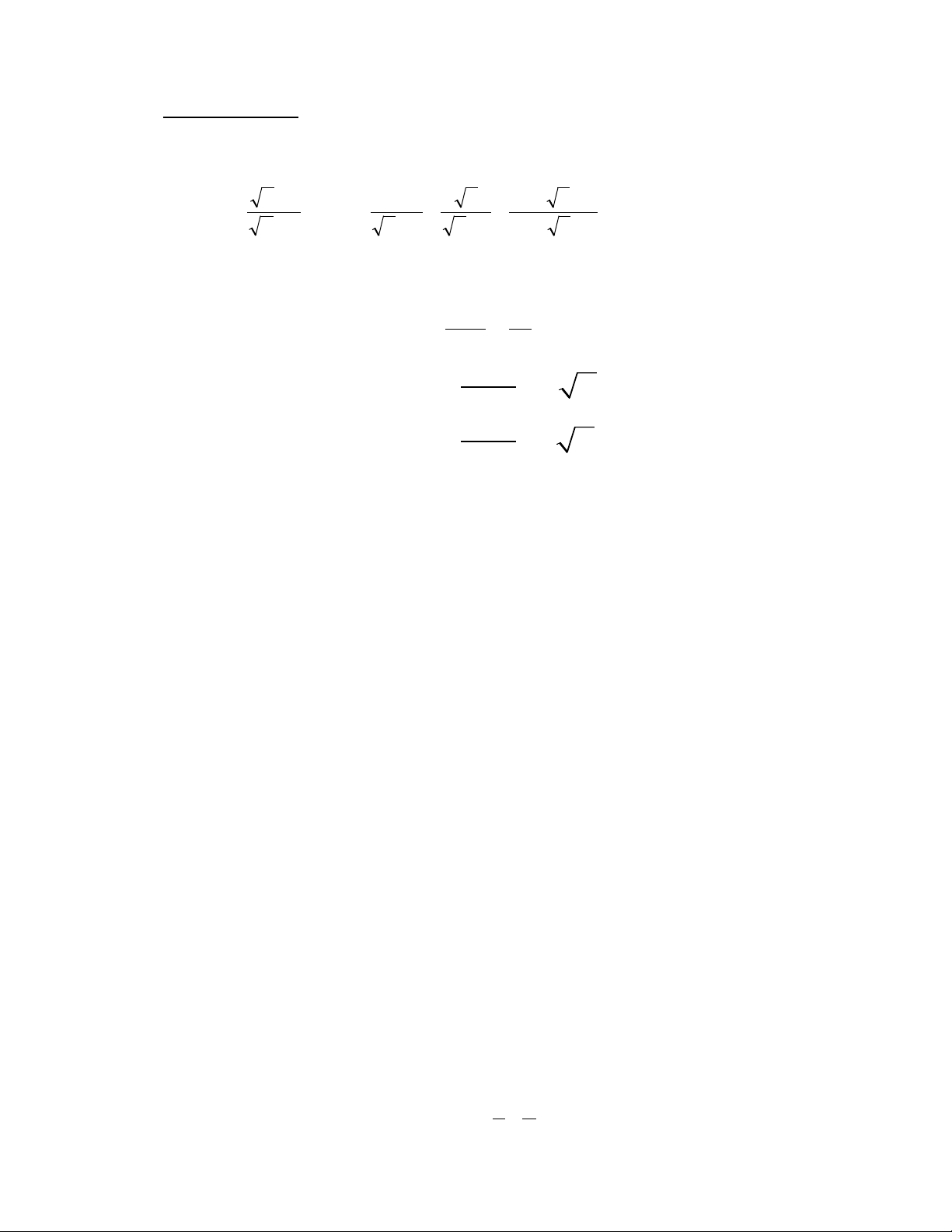
Preview text:
UBND QUẬN BẮC TỪ LIÊM
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN
TRƯỜNG THCS PHÚC DIỄN Thời gian: 120 phút Ngày 04/06/2022
Bài I (2 điểm) Cho hai biểu thức: x − 1 1 x 4 x A = và B = + − với x ≥ 0, x ≠ 1 x + 3 x + 3 x − 1 x + 2 x − 3
1) Tính giá trị biểu thức A khi x = 4
2) Rút gọn biểu thức B. A − 1 −1
3) Tìm giá trị x nguyên lớn nhất để ≤ B 2 2 + 2 y = 8 Bài II (2 điể x −1
m) 1) Giải hệ phương trình 11 − 3 y = 2 x −1 2
2) Cho parabol (P): y = x và đường thẳng (d) y=mx+1 (với m là tham số)
a) Chứng minh rằng đường thẳng (d) luôn cắt Parabol (P) tại hai điểm phân biệt.
b) Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có tung độ giao điểm
thỏa mãn y + y + y .y = 7 1 2 1 2 Bài III (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc lập hệ phương trình:
Lúc 6 giờ 30 phút sáng, một ca nô xuôi dòng từ A đến B dài 48km. Khi đến B, ca
nô nghỉ 30 phút sau đó ngược dòng từ B về A lúc 10 giờ 36 phút cùng ngày. Tìm vận tốc
riêng của ca nô biết vận tốc dòng nước là 3km/h.
2) Một hình nón có chiều cao 40cm và đường kính đáy bằng 60cm. Tính thể tích của
hình nón đó? (kết quả làm tròn đến chữ số thập phân thứ hai)
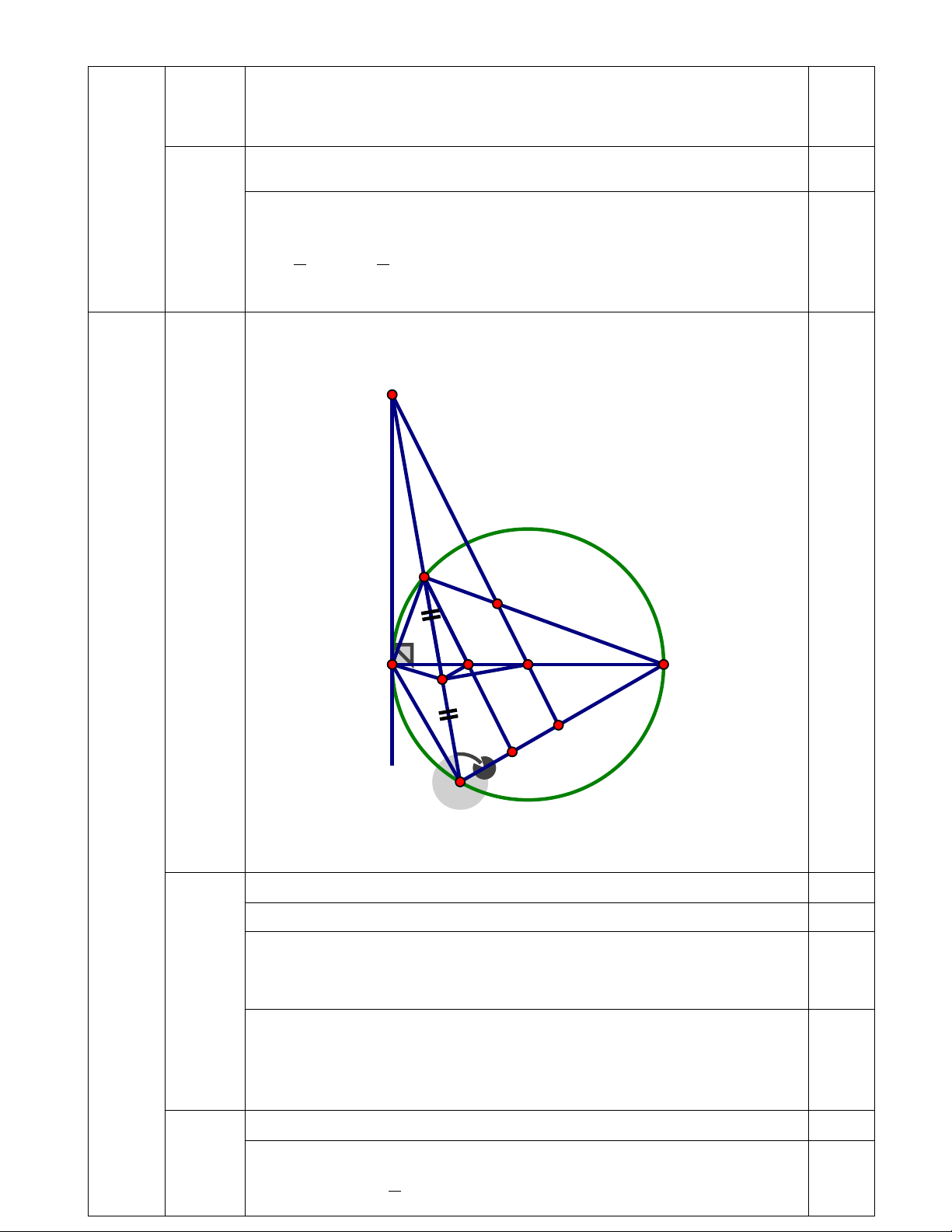
Bài IV (3 điểm) Cho đường tròn (O), đường kính AB. Trên tiếp tuyến Ax của đường tròn
(O) lấy điểm M. Qua M vẽ đường thẳng cắt đường tròn tâm O tại 2 điểm C và D (C nằm
giữa M và D, tia MD nằm giữa hai tia MO và MA). Gọi I là trung điểm của đoạn thẳng CD.
a) Chứng minh rằng: Tứ giác MAIO nội tiếp được.
b) Chứng minh rằng: MC. MD = AM2
c) Qua I kẻ đường thẳng song song với BD, cắt AB tại H. Tia MO cắt các đoạn thẳng BC
và BD lần lượt tại E, F. Chứng minh rằng: CH // EF và O là trung điểm của EF.
Bài V (0.5 điểm) Cho hai số dương x, y thỏa mãn điều kiện x + 2y = 3. 1 2
Tìm giá trị nhỏ nhất của biểu thức A = + x y Bài Câu Đáp án Điểm I
1(0,5đ) Thay x = 4 (tmđk) vào A 0,25 (2đ) Tính được A = 1/5 0,25 Trả lời: ….. 2 1 x 4 x x − 1 + x ( x + ) 3 − 4 x 0,25 B = + - = x + x − x + x − x + x − (0,75đ) 3 1 2 3 ( )( 3 ) 1 x − x − x + 0,25 1 = ( )( 1 ) 1 = ( x + )( 3 x − ) 1 ( x + )( 3 x − ) 1 x + 1 0,25 = x +3 3 0,25 A − 1 ≤ −1 ĐK: x ≥ 0, x ≠ 1 (0,75đ) B 2 Tính đượ A −1 − 4 = c B x + 1 0,25 A − 1 ≤ −1 x − 7 <=>
≤ 0 <=> x − 7 ≤ 0 B 2 2( x + 1) x ≤ 49 0,25 kết hợp x ≥ 0, x ≠ 1 0 ≤ x ≤ 49, x ≠ 1
Mà x nguyên lớn nhất, suy ra x = 49 (TMĐK) II 1
ĐKXĐ: x ≠1; y ≥ 0 0,25 (2đ)
(0,75đ) 2 0,25 + 2 y = 8 1 x −1 = 1
, giải tìm được x −1 11 − 3 y = 2 = y 3 x −1 x = 2 0,25 Từ đó: (TM ) y = 9
Kết luận: S = {(2;9 } ) . 2a
a) Xét phương trình hoành độ giao điểm của (P) và (d) ta có: 0,25 (0,5đ) 2 2
x = mx + 1 ⇔ x − mx −1 = 0 2
∆ = m + 4 > 0 ∀m nên pt luôn có 2 nghiệm phân biệt với mọi 0,25
m, suy ra đường thẳng luôn cắt Parabol tại hai điểm phân biệt
với mọi giá trị của m 2b
b) Vì pt luôn có 2 nghiệm với mọi giá trị của m, Áp dụng hệ 0,25 (0,75đ)
x + x = m thức Viet có: 1 2 x .x = 1 − 1 2
y + y + y .y = 7 0,25 1 2 1 2 2 2 2
⇔ x + x + x . 2 x = 7 1 2 1 2
⇔ (x + x )2 − 2x x + (x x )2 = 7 1 2 1 2 1 2 2 ⇔ m − .( 2 − ) 1 + (− ) 1 2 = 7 0,25 2 ⇔ m = 4 ⇔ m = 2 ± Trả lời: … III 1
Gọi vận tốc riêng của ca nô là x (đơn vị: km/h) (x > 3) 0,25 (2,5đ) (2đ)
Vận tốc xuôi dòng của ca nô là: x + 3 (km/h) 0,25
Vận tốc ngược dòng của ca nô là: x – 3 (km/h) 48 0,5
Thời gian ca nô xuôi dòng từ A đến B là: (giờ) x + 3 48
Thời gian ca nô ngược dòng từ B về A là: (giờ) x − 3
Thời gian ca nô đi từ A đến B rồi từ B trở về A, không tính thời 0,25 gian nghỉ là:
10 giờ 36 phút – 6 giờ 30 phút – 30 phút = 3 giờ 36 phút 18 = giờ. 5 Ta có phương trình: 48 48 18 0,25 + = x + 3 x − 3 5 1 − 0,25
Giải phương trình được x = 27 hoặc x = 3
Đối chiếu điều kiện và kết luận được vận tốc riêng của ca nô là 0,25 27 km/h. 2
Bán kính đáy của hình nón là: 60 : 2 = 30 (cm) 0,25
(0,5đ) Thể tích của hình nón là: 0,25 1 1 2 2 V = R π h = . .30 π .40 = 12000π ≈ 37699, ( 3 11 cm ) 3 3 IV Vẽ hình đúng câu 1 0,25 (3đ) M C E H O A B I F K D 1
Chứng minh tứ giác MAIO nội tiếp.
(0,75đ) C/m OI ⊥ CD tại I => góc MIO = 900 0,25
C/m MA là tiếp tuyến tại A của (O) 0,25
=> MA ⊥ OA tại A (t/c tiếp tuyến) => góc MAO = 900 C/m tứ giác MAIO có: 0,25 góc MIO = MAO = 900
Mà hai đỉnh A và I kề nhau
Tứ giác MAIO nội tiếp (BT quỹ tích cung chứa góc) 2
Chứng minh MC. MD = AM2 (1đ) C/m (O) có: 0,25 = 1 = s® MAC MDC ( AC) 2 Xét ∆MAC và ∆MDA có: 0,25 Góc AMD chung = MAC MDC (cmt) ⇒ ∆MAC ∆MDA (g.g) 0,25 ⇒ MA MC 0,25 =
( tỉ số đồng dạng) ⇒ AM2 = MC. MD (đpcm) MD MA 3a
Chứng minh CH // EF
(0,5đ) Ta có IH // BD (gt) 0,25 ⇒ = CIH
CDC ( 2 góc đồng vị) Xét (O): 1 Có = = s® CDB CAH ( BC) 2 Suy ra = CIH CAH
Từ đó c/m tứ giác ACHI nội tiếp ⇒ = IAH
ICH (2 góc nội tiếp cùng chắn cung IH) C/m = IAH
IMO (do tứ giác MAIO nội tiếp) 0,25 Suy ra = ICH IMO
Mà 2 góc này ở vị trí đồng vị Suy ra CH // MO
⇒ CH // EF (vì E, F, M, O thẳng hàng) 3b
Chứng minh O là trung điểm của EF.
(0,5đ) Kéo dài CH cắt BD tại K 0,25 C
∆ DK có I là trung điểm của CD, IH //DK
=> H là trung điểm của CK B ∆ OE BO CH có EO // CH ⇒ = (Hệ quả Ta - lét) CH BH B ∆ OF BO KH có OF // KH ⇒ = (Hệ quả Ta - lét) KH BH ⇒ OE OF 0,25 = CH KH
Mà CH = KH (vì H là trung điểm của CK) Suy ra OE = OF Mà O, E, F thẳng hàng
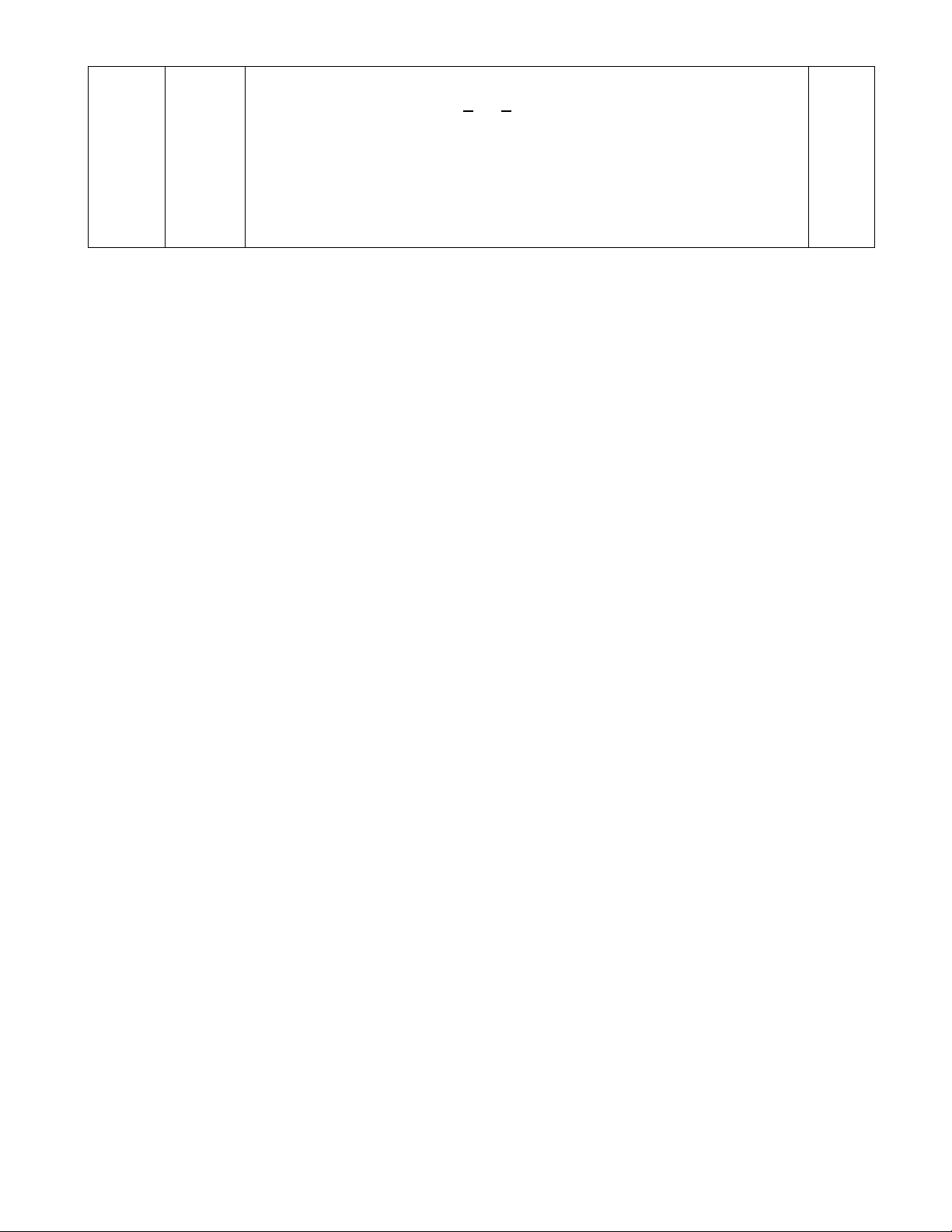
Suy ra O là trung điểm của EF V 𝐴𝐴 = 1 + 2 1 => 3A = ( + 2).(x + 2y) 0,25 (0,5đ) 𝑥𝑥 𝑦𝑦 𝑥𝑥 𝑦𝑦
=> 3A = 1+ 2. 𝑦𝑦 + 2. 𝑥𝑥 + 4 = 5 + 2(𝑥𝑥 + 𝑦𝑦) 𝑥𝑥 𝑦𝑦 𝑦𝑦 𝑥𝑥 𝑥𝑥
Do x, y > 0 => + 𝑦𝑦 ≥ 2 => 2 �𝑥𝑥 + 𝑦𝑦� ≥ 4 𝑦𝑦 𝑥𝑥 𝑦𝑦 𝑥𝑥
=> 3A ≥ 9 => 𝐴𝐴 ≥ 3 𝑥𝑥 + 2𝑦𝑦 = 3 0,25 Dấu “=” xảy ra khi �
𝑥𝑥 = 𝑦𝑦 <=> �𝑥𝑥 + 2𝑦𝑦 = 3 𝑥𝑥 = 𝑦𝑦 𝑦𝑦 𝑥𝑥 <=> �𝑥𝑥 = 1 𝑦𝑦 = 1 (TM)
Vậy GTNN của A là 3 khi x = y = 1.