Đề thi thử vào lớp 10 môn Toán năm 2022 trường THCS Thanh Xuân Trung – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi thử tuyển sinh vào lớp 10 THPT môn Toán năm 2022 trường THCS Thanh Xuân Trung, thành phố Hà Nội; kỳ thi được diễn ra vào ngày 09 tháng 06 năm 2022; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm. Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
TRƯỜNG THCS THANH XUÂN TRUNG ĐỀ THI THỬ VÀO LỚP 10 NĂM HỌC 2021-2022 MÔN: TOÁN 9 ĐỀ CHÍNH THỨC Ngày kiểm tra: 09/06/2022
(Đề kiểm tra gồm: 01 trang)
Thời gian làm bài: 120 phút
Bài I (2,0 điểm) Cho hai biểu thức: 3 x 6 1 x 3 A và x 2 B với x 0 ; x 4 x 2 x 2 x x x 1
1) Tính giá trị của biểu thức B khi x = 25. 2) Rút gọn A.
3) Tìm các số nguyên x để 2 AB . 3 Bài II (2,5 điểm)
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một người đi xe đạp từ địa điểm A đến địa điểm B với vận tốc không đổi, hai địa
điểm cách nhau 30km. Khi đi từ B về A người đó chọn đường khác dễ đi hơn nhưng dài
hơn con đường cũ 6km. Vì vậy, lúc về người đó đi với vận tốc lớn hơn vận tốc đi là
3km/h. Nên thời gian về ít hơn thời gian đi là 20 phút. Tính vận tốc lúc đi của người đó.
2) Một quả bóng hình cầu có diện tích bề mặt là 144 cm2. Tính thể tích của quả bóng đó? (Lấy 3,14 ). Bài III (2,0 điểm) 2√𝑥 − = −2
1) Giải hệ phương trình 3√𝑥 + = 8
2) Cho Parabol (P): y = x2 và đường thẳng (d): y = 2mx + 1 (với m là tham số).
a) Chứng tỏ rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt.
b) Gọi x1, x2 là hoành độ hai giao điểm của (d) và (P). Tìm m để x x . x 1 . 1 1 2 Bài IV (3 điểm)
Cho đường tròn (O) và dây BC cố định nhỏ hơn đường kính, A là điểm di động trên
cung lớn BC (AB < AC và ∆ABC nhọn). Gọi AD, BE, CF là các đường cao của tam giác ABC.
1) Chứng minh rằng: Tứ giác ACDF nội tiếp.
2) Qua D kẻ đường thẳng song song với EF cắt AB tại P và cắt AC tại Q. Chứng minh ABC AQP.
3) Gọi N là trung điểm BC và EF cắt BC tại M. Chứng minh ∆DFP cân tại D và MF.ME = MD.MN.
Bài V (0,5 điểm) Cho a, b, c là các số thực dương thỏa mãn a + b + c = 3. a b c
Tìm giá trị nhỏ nhất của biểu thức P 2 2 2 b c 1 c a 1 a b 1 ----- HẾT-----
TRƯỜNG THCS THANH XUÂN TRUNG HƯỚNG DẪN CHẤM NĂM HỌC 2021-2022 ĐỀ THI THỬ VÀO 10 ĐỀ CHÍNH THỨC Môn kiểm tra: Toán 9 Ngày kiểm tra: 09/6/2022
(Đề kiểm tra gồm: 01 trang)
(Hướng dẫn chấm gồm 4 trang) Bài Ý Đáp án Điểm
Thay x = 25 (TMĐK) vào biểu thức B ta được: 0,25 25 2 5 2 3 1 B = 1 25 1 5 1 6 2 0,25 Vậy với x = 25 thì 1 B 2 3 x 6 1 x 3 A ĐK: x 0 ; x 4 x 2 x 2 x x 3 x 6 1 x 3 A 0,25 x x 2 x 2 x
3 x 6 x x 3 x 2 x x 2 2 0,25
3 x 6 x x 2 x 3 x 6 x x 2 x x 0,25 x x 2 Bài I 2 điểm x x 1 x 1 0,25 x x 2 x 2 Với
x 0 ; x 4 => A.B= x 1 x 2 x 1 . . x 2 x 1 x 1 2 AB ÐK : x 1; x 4 3 x 1 4 x 1 9 9. x 1 4. x 1 (Do 9. x 1 0) 3 9 x 9 4 x 4 0,25 5 x 13 13 x 5 169 x Mà x 1; x 4; x Z 25 x 1;2;3;5; 6 0,25
Gọi vận tốc của người đi xe đạp từ A đến B là x (km/h ; x >0 ) 0,25
Suy ra vận tốc lúc về của người đi xe đạp là x + 3 ( km/h ) 0,25
Thời gian đi từ A đến B là (ℎ) 0,25
Quảng đường lúc về từ B đến A là 30 + 6 = 36 (km) 1 0,25
Thời gian đi về từ B đến A là (ℎ) Bài II
Lập luận để có hệ phương trình − = 0,25 2 điểm
Giải phương trình: x = 9 ( km/h); x = - 30 ( loại ) 0,5
Kết luận vận tốc của người đi xe đạp từ A đến B là 9 (km/h) 0,25
Diện tích bề mặt quả bóng hình cầu là: S= 4R2 = 144 0,25 => R = 6cm 2 4 4
Thể tích quả bóng hình cầu là: V = 3 3
R .3,14.6 904,32 cm3 3 3
Vậy thể tích quả bóng hình cầu sấp 904,32 cm2 0,25 2√𝑥 − = −2 ĐKXĐ: x ≥0; x ≠ -y 3√𝑥 + = 8 0,25 2√𝑥 − = −2 9√𝑥 + = 24 11√𝑥 = 22 1 2√𝑥 − = −2 0,25 √𝑥 = 2 2√𝑥 − = −2 𝑥 = 4 . 0,25 Bài III 2. √4 − = −2 2 điểm 𝑥 = 4 𝑥 = 4(𝑡𝑚) = 6 𝑦 = −2(𝑡𝑚)
Vậy hệ PT có nghiệm duy nhất là (4; -2) 0,25
a) PT hoành độ giao điểm của (d) và (P): x2 – 2mx - 1 = 0 (*) 0,25 a = 1; b = -2m; c = -1 a.c = -1 < 0
nên PT (*) luôn có hai nghiệm trái dấu.
2 Vậy, (d) luôn cắt (P) tại hai điểm phân biệt. 0,25 x x 2m b) Áp dụng Viet: 1 2 x .x 1 1 2
PT (*) luôn có hai nghiệm trái dấu
Mà theo yêu cầu đề bài x x . x 1 nên x 1 1 2 1 > 0 và x2 < 0
=> |x2| = - x2 => x x .x 1 x 2 x 4 (tm) 1 1 2 1 1 1 x 2 4 0,25 Thay x 1 1 = 4 và x vào x 2 1 + x2 = 2m 4 Tìm được m = 15 . 0,25 8
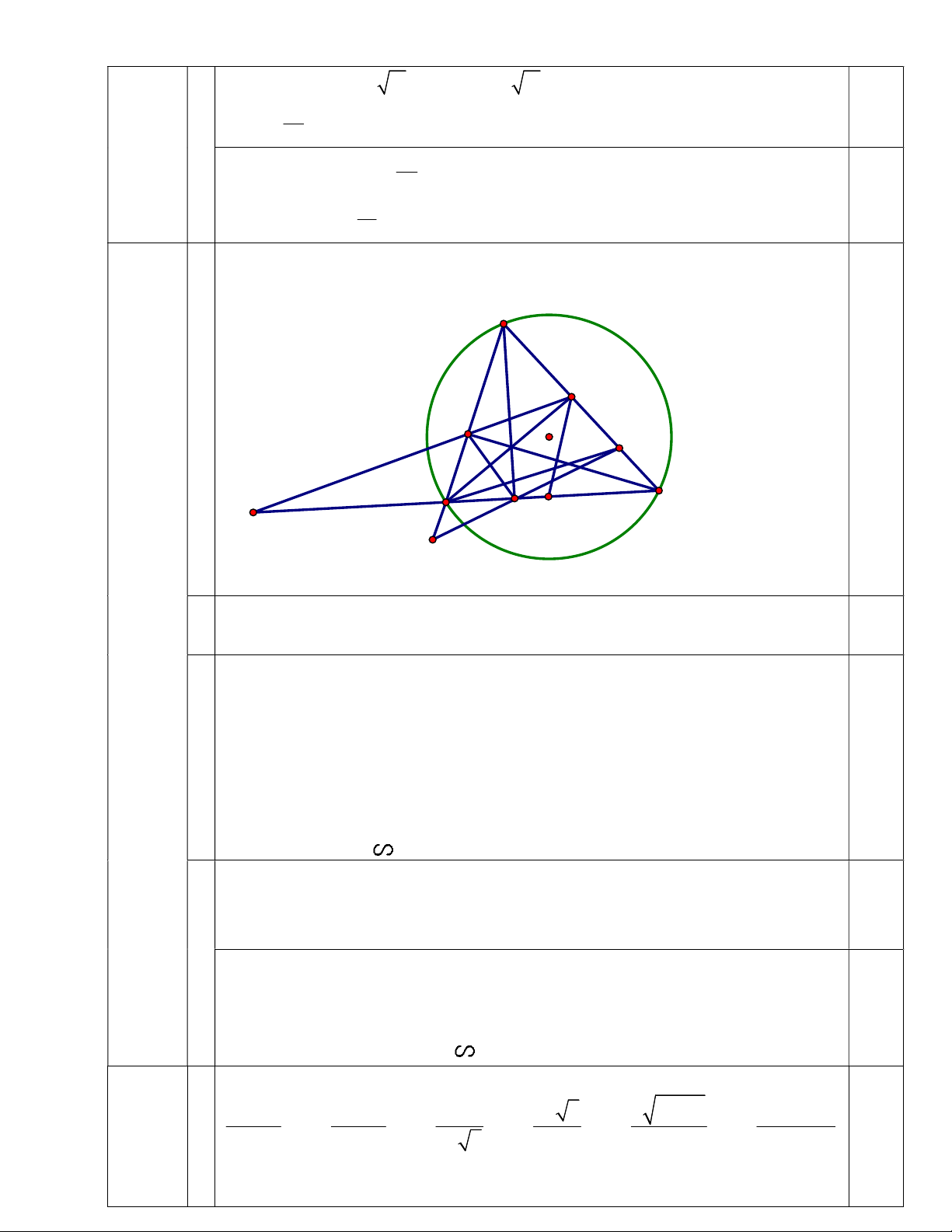
Vẽ hình đúng đến câu a A E F 0,25 O Q C B D N M P
Chứng minh được 90o; 90o AFC ADC 0,25
Bài IV 1 Chứng minh được tứ giác ACDF nội tiếp 0,5 3,5 điểm ABC và AQP
Chỉ ra được góc A chung 0,25 Chứng minh được AFE APQ (1) 0,25
2 Chứng minh được tứ giác BFEC nội tiếp ACB AFE (2) 0,25 Từ (1) và (2) => ACB APQ
Kết luận :ABC AQP (g.g) 0,25
Vì tứ giác ACDF nội tiếp (cmt) suy ra PFD BCE 0,25 mà BPD BCE
Do đó tam giác DFP cân tại D 0,25
3 Ta có tam giác BEC vuông và N là trung điểm của BC nên BNE 2 ECB BFD ECB AFE => BNE EFD 0 2ECB 180 2 BFD 0,25 Do đó 180o BNE EFD
suy ra tứ giác DFEN nội tiếp 0,25
Chứng minh được ∆MED ∆MNF suy ra MF.ME = MD.MN
Áp dụng bất đẳng thức cô si ta có: Bài V 2 2 a ab c ab c ab c b aac ba ac 0,5 a a a a a 2 2 b c 1 b c 1 2b c 2 2 4 điểm a 1 Suy ra ta có a ab abc 2 b c 1 4 Tương tự có b 1 b bc abc c 1 ; c ca abc 0,25 2 2 c a 1 4 a b 1 4
Cộng vế với vế các bất đẳng thức trên ta có: a b c ab bc ca 3abc 3 2 2 2 b c 1 c a 1 a b 1 4 4 abc Ta có 3 3 3
3 a b c 3 abc 4 4 Do đó ta được a b c 3 3 a b c 3 3 hay 2 2 2 2 2 2 b c 1 c a 1 a b 1 4 4 b c 1 c a 1 a b 1 2
Đẳng thức xảy ra khi a = b = c = 1 0,25 TỔNG ĐIỂM: 10,0
Lưu ý: Nếu HS làm theo cách khác có kết quả đúng vẫn cho điểm tối đa.
---------------------------Hết------------------------- BGH DUYỆT TTCM DUYỆT GIÁO VIÊN RA ĐỀ Đoàn Thu Huyền