HỌC VIỆN CỘNG NGHỆ BC-VT
ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1
BỘ MÔN KHOA HỌC MÁY TÍNH
MÔN: TRÍ TUỆ NHÂN TẠO Lớp: D08CNTT
Hệ đào tạo: Đại học chính quy Ngày thi: 3/06/2011 Thời gian thi: 90 phút Đề số: 1
Câu 1 (2,5 điểm): Cho đồ thị như trên hình vẽ, S là nút xuất phát, G là nút đích. Các số nằm cạnh
cung là giá thành đường đi, số nằm trong vòng tròn là giá trị hàm heuristic.
a) Hãy sử dụng thuật toán A* sâu
dần (IDA*) với α = 8 là giá trị được 5 4 2 1 3
thêm vào ngưỡng sau mỗi vòng lặp A C E 3 6
để tìm đường đi từ nút xuất phát tới đ 4 1 0
ích. Thể hiện các giá trị: nút được 1 S 1 G
mở rộng, danh sách nút mở và giá trị 5 1 4 6
hàm f tại mỗi bước. Xác định đường đ B D F i do IDA* tìm được 4 2
b) Đường đi tìm được ở câu a có
phải là đường đi tối ưu hay không ? Hãy giải thích tại sao có trường hợp IDA* không tìm được đường đi tối ưu.
Câu 2 (2,5 điểm): Cho cơ sở tri thức KB sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ:
- Gấu trúc là gấu. x(B(x) ⇒ ∀ G(x))
- Po là gấu trúc. B(Po)
- Gấu trúc thích ăn lá. x(B(x) ⇒ ∀ ( A x, Lá))
- Po biết kungfu. K (Po)
a) Viết truy vấn câu sau “Có con gấu thích ăn lá và biết kungfu” dưới dạng logic vị từ sử dụng các vị từ đã cho.
b) Chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
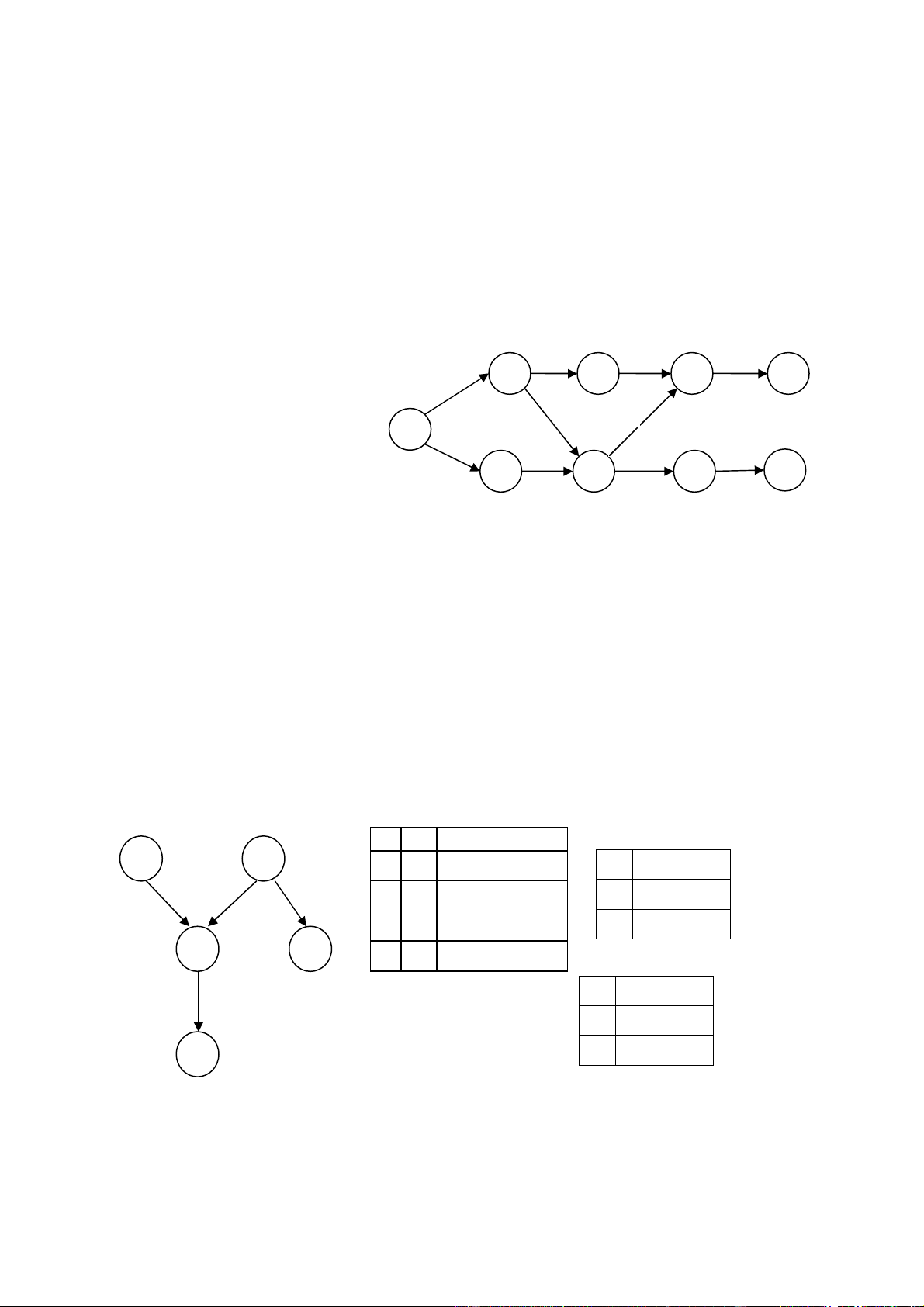
Câu 3 (2 điểm): Cho mạng Bayes sau, các biến có thể nhận giá trị {T,F} ({true, false}) P(H)= 0.2 P(A) = 0.5 H A P(B | A, H) H A A P(C|A) F F 0.7 F T 0.2 T 0.5 T F 0.1 F 0.3 B C T T 0.5 B P(D|B) T 0.3 F 0.5 D
a) Tính xác suất cả năm biến cùng nhận giá trị F. b) Tính P(A|C).
c) Mạng đã cho có dạng Polytree hay không ?
Câu 4 (3 điểm): Cho dữ liệu huấn luyện như trong Màu Hình dạng KL f
bảng (f là nhãn phân loại).
a) Hãy xác định nhãn cho ví dụ (Màu: Trắng, Hình Xanh Tròn Nặng +
dạng: Tròn, KL: Nặng) bằng phương pháp Bayes đơn Đỏ Tròn Nhẹ -
giản (chỉ rõ các xác suất điều kiện thành phần)
b) Hãy xác định nút gốc cho cây quyết định sử dụng Xanh Méo Nhẹ + thuật toán ID3 Trắng Méo Nặng + Đỏ Méo Nặng - Trắng Tròn Nhẹ - Trắng Méo Nhẹ + TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ Hoàng Xuân Dậu
Ngô Phương Nhung, Từ Minh Phương
Ghi chú: Sinh viên không được sử dụng tài liệu khi làm bài. Cán bộ coi thi không giải thích gì thêm
HỌC VIỆN CỘNG NGHỆ BC-VT
ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1
BỘ MÔN KHOA HỌC MÁY TÍNH
MÔN: TRÍ TUỆ NHÂN TẠO Lớp: D08CNTT
Hệ đào tạo: Đại học chính quy Ngày thi: 3/06/2011 Thời gian thi: 90 phút Đề số: 2
Câu 1 (2,5 điểm): Cho đồ thị như trên hình vẽ, S là nút xuất phát, G1, G2 là các nút đích. Các số
nằm cạnh cung là giá thành đường đi, số nằm trong vòng tròn là giá trị hàm heuristic.
a) Hãy sử dụng thuật toán A* để tìm
đường đi từ nút xuất phát tới đích 5 4 2 1 3 0
(G1 hoặc G2). Thể hiện các giá trị: A C E 6 G2 3
nút được mở rộng, danh sách nút mở 4 1
và giá trị hàm f tại mỗi bước. Xác 1 đị S
nh đường đi do A* tìm được. 5 1 4 1 0
b) Giải thích tại sao A* luôn tìm đượ B D F G1
c đường đi tối ưu với đồ thị đã 4 2 2 cho.
Câu 2 (2,5 điểm): Cho cơ sở tri thức KB sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ:
- Gấu trúc là gấu. x(P(x) ⇒ ∀ B(x))
- Po là gấu trúc. P(Po)
- Gấu trúc thích ăn lá. x(P(x) ⇒ ∀
E(x, Lá))
- Po biết kungfu. K (Po)
a) Viết câu truy vấn sau “Gấu thích ăn lá hoặc biết kungfu” dưới dạng logic vị từ sử dụng các vị từ đã cho.
b) Chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
Câu 3 (2 điểm): Cho mạng Bayes sau, các biến có thể nhận giá trị {T,F} ({true, false}) P(H)= 0.2 P(A) = 0.5 H A P(B | A, H) H A A P(C|A) F F 0.7 F T 0.2 T 0.5 T F 0.1 F 0.3 B C T T 0.5 B P(D|B) T 0.3 F 0.5 D
a) Tính xác suất A, B, D nhận giá trị T và H, C nhận giá trị F. b) Tính P(H|B).
c) Giá trị của D có độc lập xác suất với A không khi biết giá trị của C ?
Câu 4 (3 điểm): Cho dữ liệu huấn luyện như trong Màu Hình dạng KL f
bảng (f là nhãn phân loại).
a) Hãy xác định nhãn cho ví dụ (Màu: Trắng, Hình Xanh Tròn Nặng -
dạng: Tròn, KL: Nặng) bằng phương pháp Bayes đơn Đỏ Tròn Nhẹ +
giản (chỉ rõ các xác suất điều kiện thành phần)
b) Hãy xác định nút gốc cho cây quyết định sử dụng Xanh Tròn Nhẹ - thuật toán ID3 Trắng Méo Nặng - Đỏ Méo Nặng + Trắng Tròn Nhẹ + Trắng Méo Nhẹ - TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ Hoàng Xuân Dậu
Ngô Phương Nhung, Từ Minh Phương
Ghi chú: Sinh viên không được sử dụng tài liệu khi làm bài. Cán bộ coi thi không giải thích gì thêm
HỌC VIỆN CỘNG NGHỆ BC-VT
ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1
BỘ MÔN KHOA HỌC MÁY TÍNH
MÔN: TRÍ TUỆ NHÂN TẠO Lớp: D08CNTT
Hệ đào tạo: Đại học chính quy Ngày thi: 3/06/2011 Thời gian thi: 90 phút Đề số: 3
Câu 1 (2,5 điểm): Cho đồ thị như trên hình vẽ, S là nút xuất phát, G là nút đích. Các số nằm cạnh
cung là giá thành đường đi, số nằm trong vòng tròn là giá trị hàm heuristic.
a) Hãy sử dụng thuật toán A* sâu
dần (IDA*) với α = 8 là giá trị được 5 4 2 1 3
thêm vào ngưỡng sau mỗi vòng lặp A C E 3 6
để tìm đường đi từ nút xuất phát tới đ 4 1 0
ích. Thể hiện các giá trị: nút được 1 S G
mở rộng, danh sách nút mở và giá trị 5 5 1 4 5
hàm f tại mỗi bước. Xác định đường đ B D F i do IDA* tìm được 4 2
b) Đường đi tìm được ở câu a có
phải là đường đi tối ưu hay không ? Hãy giải thích tại sao có trường hợp, IDA* không tìm được đường đi tối ưu.
Câu 2 (2,5 điểm): Cho cơ sở tri thức KB sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ:
- Cá biết bơi. x(C(x) ⇒ ∀ B(x))
- Chim cánh cụt biết bơi. x
∀ (P(x) => B(x))
- Tất cả chim cánh cụt đều thích ăn một loại cá nào đấy. x(P(x) ⇒ ∀
∃y(C(y) ∧ L(x, y))
- Ted là chim cánh cụt. P(Ted )
a) Viết câu sau “Ted thích ăn một số sinh vật biết bơi” dưới dạng logic vị từ sử dụng các vị từ đã cho.
b) Chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
Câu 3 (2 điểm): Cho mạng Bayes sau, các biến có thể nhận giá trị {T,F} ({true, false}) P(H)= 0.2 P (A) = 0.5 P(D)=0.4 H A P(B =T | A, H) A D P(C=T|A,D) H A D F F 0.7 F F 0.8 F T 0.2 F T 0.3 T F 0.1 T F 0.4 B C T T 0.5 T T 0.2
a) Tính xác suất cả năm biến cùng nhận giá trị F. b) Tính P(A|C).
c) Theo mạng đã cho H và B có độc lập xác suất với nhau không ?
Câu 4 (3 điểm): Cho dữ liệu huấn luyện như trong Màu Độ dài KL f
bảng (f là nhãn phân loại).
a) Hãy xác định nhãn cho ví dụ (Màu: Trắng, Độ dài: Xanh Dài Nặng +
Dài, KL: Nặng) bằng phương pháp Bayes đơn giản Đỏ Dài Nhẹ -
(chỉ rõ các xác suất điều kiện thành phần)
b) Hãy xác định nút gốc cho cây quyết định sử dụng Xanh Ngắn Nhẹ + thuật toán ID3 Trắng Ngắn Nặng + Đỏ Ngắn Nặng - Trắng Dài Nhẹ + Trắng Ngắn Nhẹ + TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ Hoàng Xuân Dậu
Ngô Phương Nhung, Từ Minh Phương
Ghi chú: Sinh viên không được sử dụng tài liệu khi làm bài. Cán bộ coi thi không giải thích gì thêm
HỌC VIỆN CỘNG NGHỆ BC-VT
ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1
BỘ MÔN KHOA HỌC MÁY TÍNH
MÔN: TRÍ TUỆ NHÂN TẠO Lớp: D08CNTT
Hệ đào tạo: Đại học chính quy Ngày thi: 3/06/2011 Thời gian thi: 90 phút Đề số: 4
Câu 1 (2,5 điểm): Cho đồ thị như trên hình vẽ, S là nút xuất phát, G1, G2 là các nút đích. Các số
nằm cạnh cung là giá thành đường đi, số nằm trong vòng tròn là giá trị hàm heuristic.
a) Hãy sử dụng thuật A*để tìm
đường đi từ nút xuất phát tới đích 5 4 2 1 3 0
(G1 hoặc G2). Thể hiện các giá trị: A C E 6 G1 3
nút được mở rộng, danh sách nút mở 4 1
và giá trị hàm f tại mỗi bước. Xác 1 đị S
nh đường đi do A* tìm được 5 1 4 5 5 0
b) Giải thích tại sao A* luôn tìm đượ B D F G2
c đường đi tối ưu với đồ thị đã 4 2 cho.
Câu 2 (2,5 điểm): Cho cơ sở tri thức KB sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ:
- Cá biết bơi. x(F (x) ⇒ ∀ S (x))
- Chim cánh cụt biết bơi. x
∀ (P(x) => S(x))
- Tất cả chim cánh cụt đều thích ăn một loại cá nào đấy. x(P(x) ⇒ ∀
∃y(F(y) ∧ L(x, y))
- Ted là chim cánh cụt. P(Ted )
a) Viết câu sau “Có chim cánh cụt thích ăn một số sinh vật biết bơi” dưới dạng logic vị từ sử dụng các vị từ đã cho.
b) Chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
Câu 3 (2 điểm): Cho mạng Bayes sau, các biến có thể nhận giá trị {T,F} ({true, false}) P(H)= 0.3 P (A) = 0.5 P(D)=0.7 H A P(B =T | A, H) A D P(C=T|A,D) H A D F F 0.3 F F 0.3 F T 0.2 F T 0.3 T F 0.6 T F 0.8 B C T T 0.5 T T 0.2
a) Tính xác suất cả năm biến cùng nhận giá trị T. b) Tính P(A|B).
c) Theo mạng đã cho B và C có độc lập xác suất với nhau khi biết giá trị của D không ?
Câu 4 (3 điểm): Cho dữ liệu huấn luyện như trong Màu Độ dài KL f
bảng (f là nhãn phân loại). Xanh Dài Nặng -
a) Hãy xác định nhãn cho ví dụ (Màu: Xanh, Độ dài:
Dài, KL: Nhẹ) bằng phương pháp Bayes đơn giản (chỉ Đỏ Dài Nhẹ +
rõ các xác suất điều kiện thành phần)
b) Hãy xác định nút gốc cho cây quyết định sử dụng Xanh Ngắn Nhẹ - thuật toán ID3 Trắng Ngắn Nặng - Đỏ Ngắn Nặng + Trắng Dài Nhẹ - Trắng Ngắn Nhẹ - TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ Hoàng Xuân Dậu
Ngô Phương Nhung, Từ Minh Phương
Ghi chú: Sinh viên không được sử dụng tài liệu khi làm bài. Cán bộ coi thi không giải thích gì thêm
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1 MÔN: Trí tuệ nhân tạo
BỘ MÔN: Khoa học máy tính
Lớp: D07CNTT Hệ đào tạo: - Đại học Thời gian thi: 90 phút Đề số: 1
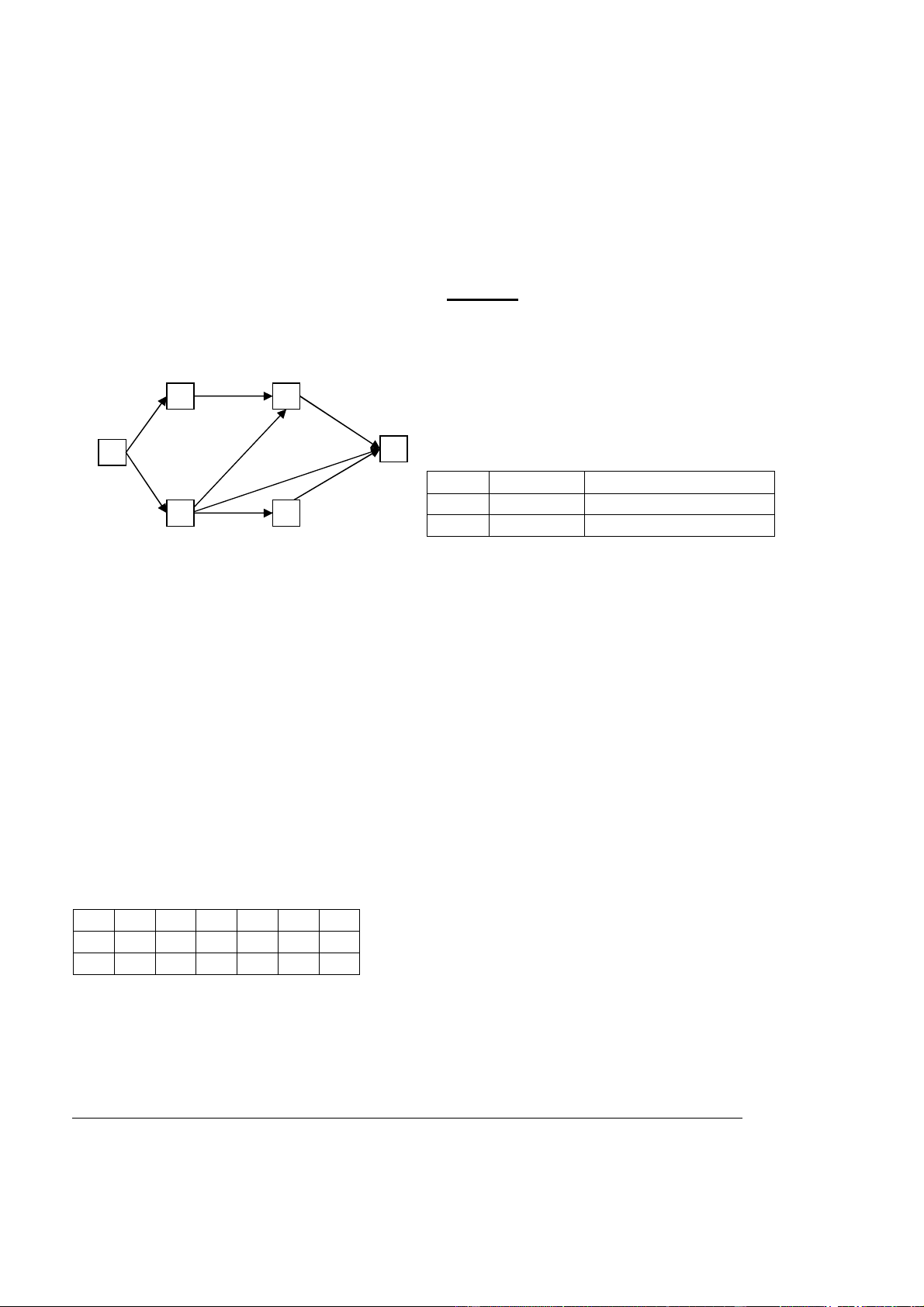
Câu 1. (2,5 điểm) Tìm đường đi từ S tới G trên đồ thị sau bằng cách sử dụng: a) Tìm kiếm tham lam, h = 4 h = 2 b) Tìm theo chiều sâu. 4 B C
Giá thành đường đi cho trên cạnh. Giá trị hàm heuristic h cho 3 2
bên cạnh nút. Thể hiện thuật toán bằng cách điền vào bảng
sau giá trị nút được chọn và danh sách các nút mở (cùng với S 1 1 G
giá trị hàm h trong trường hợp tìm tham lam) sau mỗi bước. h = 6 h = 0 2 Bước Nút chọn
Danh sách nút mở và h 3 3 1 A D … h = 4 h = 2
(Với các nút tương đương chọn theo thứ tự chữ cái)
Câu 2. (2,5 điểm) Cho các mệnh đề sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ
- Máy tính mới thì chạy nhanh. x(M (x) ⇒ ∀ N (x))
- Máy tính phòng thực hành chạy chậm. x(T (x) ⇒ ∀ ¬N(x))
- Một số máy phòng thực hành rất đẹp. x
∃ (T (x) ∧ Đ(x))
a) Viết các câu trên dưới dạng CNF (clause form)
b) Viết câu truy vấn sau “Có những máy tính đẹp nhưng chậm” dưới dạng lôgic vị từ sử dụng các vị từ đã cho
ở trên; và chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
Câu 3. (2,5 điểm) Giả sử một loại virus (biểu diễn bằng biến ngẫu nhiên V) có thể gây ra ba hậu quả sau: mất
file (biến F), máy chạy chậm (biến C), máy tự khởi động lại (biến R). Biết xác suất mất file khi không nhiễm
và có nhiễm virus là 0.05 và 0.6; xác suất máy chạy chậm khi không nhiễm virus và có nhiễm là 0.2 và 0.7;
xác suất máy tự khởi động khi không virus và có virus là 0.05 và 0.5. Quan sát cho thấy số máy nhiễm loại
virus này là 20 trên 100 máy.
a) Vẽ mạng Bayes và bảng xác suất điều kiện cho ví dụ này.
b) Máy tính phòng thực hành chạy chậm. Tính xác suất máy đó nhiễm virus.
Câu 4. (2,5 điểm) Cho dữ liệu huấn luyện dưới đây. Các dòng A, B, C là thuộc tính, D là nhãn phân loại. A 2 2 1 1 2 1 B 1 2 1 2 1 1 C 1 2 1 1 2 2 D + + + + - -
Xây dựng cây quyết định sử dụng thuật toán ID3 cho dữ liệu trên. TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ
Ghi chú: - Sinh viên không được tham khảo tài liệu. - Cán bộ coi thi không giải thích gì thêm
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1 MÔN: Trí tuệ nhân tạo
BỘ MÔN: Khoa học máy tính
Lớp: D07CNTT Hệ đào tạo: - Đại học Thời gian thi: 90 phút Đề số: 2
Câu 1. (2,5 điểm) Tìm đường đi từ S tới G trên đồ thị sau bằng cách sử dụng: a) Tìm kiếm A* h = 4 h = 2 b) Tìm theo chiều sâu. 4 B C
Giá thành đường đi cho trên cạnh. Giá trị hàm heuristic h cho 3 2
bên cạnh nút. Thể hiện thuật toán bằng cách điền vào bảng
sau giá trị nút được chọn và danh sách các nút mở (cùng với S 1 1 G
giá trị hàm f trong trường hợp A*) sau mỗi bước. h = 6 h = 0 2 Bước Nút chọn
Danh sách nút mở và f 3 3 1 A D … h = 4 h = 2
(Với các nút tương đương chọn theo thứ tự chữ cái)
Câu 2. (2,5 điểm) Cho các mệnh đề sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ
- Những người biết lập trình và biết dùng máy tính đều hay lướt Web. x
∀ (P(x) C(x) ⇒ ∧ W (x))
- Ai biết lập trình đều dùng được máy tính. x(P(x) ⇒ ∀ C(x))
- Nam biết lập trình. P(Nam)
a) Viết các câu trên dưới dạng CNF (clause form)
b) Viết câu truy vấn sau “Có những người hay lướt Web” dưới dạng lôgic vị từ sử dụng các vị từ đã cho ở
trên; và chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
Câu 3. (2,5 điểm) Cho ba triệu chứng sau: sốt (ký hiệu bằng biến ngẫu nhiên S), ho (ký hiệu H), và đau đầu
(ký hiệu Đ) có thể có cùng một nguyên nhân là do một loại bệnh (ký hiệu B) gây ra. Xác suất ho khi bị bệnh
và không bị bệnh lần lượt là 0.8 và 0.1; xác suất sốt khi bị bệnh và không bị bệnh là 0.9 và 0.05; xác suất đau
đầu khi bị bệnh và không bị bệnh là 0.8 và 0.25. Số lượng bệnh nhân bị bệnh này chiếm 10% dân số.
a) Vẽ mạng Bayes và bảng xác suất điều kiện cho ví dụ này.
b) Một bệnh nhân nhập viện với biểu hiện ho. Hãy cho biết người này có bị bệnh B không.
Câu 4. (2,5 điểm) Cho dữ liệu huấn luyện dưới đây. Các dòng A, B, C là thuộc tính, D là nhãn phân loại. A 2 2 1 1 2 1 B 1 2 1 2 1 1 C 1 2 1 1 2 2 D + + + + - -
Sử dụng phân loại Bayes đơn giản để xác định nhãn phân loại cho hai trường hợp sau: (A=1, B=2, C=2) và (A=2, B=2, C=1). TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ
Ghi chú: - Sinh viên không được tham khảo tài liệu. - Cán bộ coi thi không giải thích gì thêm
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1 MÔN: Trí tuệ nhân tạo
BỘ MÔN: Khoa học máy tính
Lớp: D07CNTT Hệ đào tạo: - Đại học Thời gian thi: 90 phút Đề số: 3
Câu 1. (2,5 điểm) Tìm đường đi từ S tới G trên đồ thị sau bằng cách sử dụng: a) Tìm kiếm tham lam, h = 4 h = 2 b) Tìm theo chiều sâu. 4 B C
Giá thành đường đi cho trên cạnh. Giá trị hàm heuristic h cho 3 1
bên cạnh nút. Thể hiện thuật toán bằng cách điền vào bảng
sau giá trị nút được chọn và danh sách các nút mở (cùng với S 1 G
giá trị hàm h trong trường hợp tìm tham lam) sau mỗi bước. 4 h = 6 h = 0 2 Bước Nút chọn
Danh sách nút mở và h 3 3 1 A D … h = 3 h = 2
(Với các nút tương đương chọn theo thứ tự chữ cái)
Câu 2. (2,5 điểm) Cho các mệnh đề sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ
- Mọi máy tính xách tay đều nhẹ. x(L(x) ⇒ ∀ N (x))
- Máy tính ở phòng thực hành nhẹ nhưng không nhanh. x(T (x) ⇒ ∀
(N (x) ∧ ¬F (x)))
- Mọi máy tính xách tay đều nhanh. x(L(x) ⇒ ∀ F (x))
a) Viết các câu trên dưới dạng CNF (clause form)
b) Viết câu truy vấn sau “Máy ở phòng thực hành không phải máy tính xách tay” dưới dạng lôgic vị từ sử
dụng các vị từ đã cho ở trên; và chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
Câu 3. (2,5 điểm) Cho biết 60% dân số thường xuyên ăn rau sống. Có 40% người ăn rau sống nhiễm bệnh
đường ruột và 10% người không ăn rau sống bị bệnh. Nếu bị bệnh thì bị đau bụng với xác suất 80%, và bị
chán ăn với xác suất 70%. Nếu không bị bệnh cũng có thể đau bụng với xác suất 10% và chán ăn với xác suất
20%. Ký hiệu ăn rau sống, nhiễm bệnh, đau bụng, chán ăn tương ứng bằng các biến ngẫu nhiên R, B, Đ, C.
a) Vẽ mạng Bayes và bảng xác suất điều kiện cho ví dụ này.
b) Một người bệnh bị đau bụng. Hãy xác định người đó có nhiễm bệnh đường ruột không.
Câu 4. (2,5 điểm) Cho dữ liệu huấn luyện dưới đây. Dòng A và B là thuộc tính, dòng C là nhãn phân loại. A 2 2 3 3 1 1 B 1 2 1 2 1 2 C - - + + + -
Xây dựng cây quyết định cho dữ liệu trên sử dụng thuật toán ID3. TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ
Ghi chú: - Sinh viên không được tham khảo tài liệu. - Cán bộ coi thi không giải thích gì thêm
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG ĐỀ THI KẾT THÚC MÔN HỌC
KHOA CÔNG NGHỆ THÔNG TIN 1 MÔN: Trí tuệ nhân tạo
BỘ MÔN: Khoa học máy tính
Lớp: D07CNTT Hệ đào tạo: - Đại học Thời gian thi: 90 phút Đề số: 4
Câu 1. (2,5 điểm) Tìm đường đi từ S tới G trên đồ thị sau bằng cách sử dụng: a) Tìm kiếm A* h = 4 h = 2 b) Tìm theo chiều sâu. 4 B C
Giá thành đường đi cho trên cạnh. Giá trị hàm heuristic h cho 3 1
bên cạnh nút. Thể hiện thuật toán bằng cách điền vào bảng
sau giá trị nút được chọn và danh sách các nút mở (cùng với S 1 G
giá trị hàm f trong trường hợp A*) sau mỗi bước. 4 h = 6 h = 0 2 Bước Nút chọn
Danh sách nút mở và f 3 3 1 A D … h = 3 h = 2
(Với các nút tương đương chọn theo thứ tự chữ cái)
Câu 2. (2,5 điểm) Cho các mệnh đề sau dưới dạng ngôn ngữ tự nhiên và lôgic vị từ
- Những người học CNTT đều biết lập trình. x(C( x) ⇒ ∀ L( x))
- Trẻ em không biết lập trình. x(E( x) ⇒ ∀ ¬L(x))
- Một số trẻ em giỏi toán. x
∃ (E(x) ∧ T (x))
a) Viết các câu trên dưới dạng CNF (clause form)
b) Viết câu truy vấn sau “Có một số người giỏi toán không biết lập trình” dưới dạng lôgic vị từ sử dụng các vị
từ đã cho ở trên; và chứng minh câu truy vấn đúng sử dụng phép giải và phản chứng.
Câu 3. (2,5 điểm) Cho biết 60% người viêm họng bị sốt cao và 90% người viêm họng bị đau họng. Khi không
viêm họng chỉ có 10% sốt cao và 5% đau họng. Khi sốt cao thì có 80% chán ăn. Có 15% người không sốt cao
bị chán ăn. Thống kê cho thấy khoảng 20% dân số viêm họng.
a) Vẽ mạng Bayes và bảng xác suất điều kiện cho ví dụ này.
b) Tính xác suất một người bị viêm họng nếu biết người này sốt cao.
Câu 4. (2,5 điểm) Cho dữ liệu huấn luyện dưới đây. Dòng A, B và C là thuộc tính, dòng D là nhãn phân loại. A 2 2 3 3 1 1 1 2 B 1 2 1 2 1 2 1 2 C 1 2 1 2 1 2 2 2 D - - + + + - + +
Sử dụng phân loại Bayes đơn giản để xác định nhãn D cho hai trường hợp (A=1, B=2, C=1) và (A=2, B=2, C=2). TRƯỞNG BỘ MÔN DUYỆT GIÁO VIÊN RA ĐỀ
Ghi chú: - Sinh viên không được tham khảo tài liệu. - Cán bộ coi thi không giải thích gì thêm