Đề thi tuyển sinh 10 môn toán PTDTNT tỉnh năm 2019-2020 môn toán Sở GD Quảng Nam (có đáp án và lời giải chi tiết)
Tổng hợp Đề thi tuyển sinh 10 môn toán PTDTNT tỉnh năm 2019-2020 môn toán Sở GD Quảng Nam (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Chủ đề: Đề thi vào 10 môn Toán năm 2019-2020
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TRƯỜNG PTDTNT TỈNH QUẢNG NAM Năm học: 2019-2020 Môn thi : TOÁN ĐỀ CHÍNH THỨC
Thời gian : 120 phút (không kể thời gian giao đề) (Đề có 01 trang) Ngày thi : 03/6/2019
Câu 1 (2,0 điểm). 6
a) Thực hiện phép tính: 18 8. 3 x 2 x 2 x 4
b) Rút gọn biểu thức: P
với x 0 và x 4. x 4 x 4 x 4
Câu 2 (2,0 điểm).
a) Vẽ đồ thị của hàm số 2 y 2x .
b) Xác định các hệ số a, b của hàm số y ax b biết đồ thị của nó song song với đường
thẳng y 2x 3 và đi qua điểm A(1;2).
Câu 3 (2,5 điểm). a) Giải phương trình 2
x 7x 10 0 .
x 3y 3
b) Giải hệ phương trình .
2x y 4 c) Cho phương trình 2
x 4x 2m 1 0 (1), với m là tham số. Tìm m để phương trình (1)
có hai nghiệm phân biệt x , x sao cho x x 2. 1 2 1 2
Câu 4 (3,5 điểm).
Cho đường tròn (O ; R) có đường kính BC. Trên tia đối của tia BC, lấy điểm A sao cho
BO = 2BA. Vẽ tiếp tuyến AD với đường tròn (O) (D là tiếp điểm) và dây cung DE của đường
tròn (O) vuông góc với BC.
a) Tính độ dài đoạn thẳng AD theo R.
b) Chứng minh AE là tiếp tuyến của đường tròn (O).
c) Vẽ đường kính DF của đường tròn (O). Gọi P là giao điểm của EC và DF, G là giao
điểm của hai đường thẳng BD và AE. Chứng minh BC // EF và PO . GE = PC . GB.
d) Vẽ cát tuyến AMN của đường tròn (O) (cát tuyến không đi qua O), các tiếp tuyến tại M
và N của đường tròn (O) cắt nhau tại K. Chứng minh ba điểm K, D, E thẳng hàng.
--------------- Hết ---------------
Họ và tên thí sinh: ........................................................................... SBD: ....................................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TRƯỜNG PTDTNT TỈNH QUẢNG NAM Năm học: 2019-2020 HDC CHÍNH THỨC HƯỚNG DẪN CHẤM
(Bản hướng dẫn này gồm 02 trang) Câu Nội dung Điểm 6
a) Thực hiện phép tính: 18 8. 1,0 3 6 18 3 2 ,
2 , 8 2 2 (mỗi ý đúng: 0,25 đ) 0,75 3
Tính đúng kết quả bằng 2 2 0,25 Câu 1 x 2 x 2 x 4
b) Rút gọn biểu thức P
, với x 0 và x 4. 1,0 (2,0) x 4 x 4 x 4
Biến đổi được x 2 x x ( x 2) x
(mỗi ý đúng: 0,25đ) 0,5 2 x 4 x 4 ( x 2) x 2
Biến đổi được 2 x 4 2( x 2) 2 0,25 x 4
( x 2)( x 2) x 2 Suy ra được P 1. 0,25
a) Vẽ đồ thị của hàm số 2 y 2x . 1,0
+ Xác định 3 điểm đi qua: O(0;0), A(-1;2), B(1;2) (đúng tọa độ 1 điểm: 0,25 đ). 0,5
+ Vẽ chính xác đồ thị (vẽ đúng dạng: 0,25 đ). 0,5 Câu 2
b) Xác định các hệ số a, b của hàm số y ax b biết đồ thị của nó song song với (2,0) đường thẳng 1,0 y 2
x 3 và đi qua điểm A(1;2).
+ Lập luận suy ra được a 2 0,5
+ Đường thẳng y ax b đi qua điểm A(1; 2) nên a b 2 (1) 0,25 Thay a 2
vào (1) suy ra được b 4. Vậy a 2 , b 4. 0,25
a) Giải phương trình 2
x 7x 10 0 . 0,75 + Tính đúng 9 0,25
+ Tìm được 2 nghiệm là: 1 x 2 , 2
x 5 (đúng mỗi nghiệm: 0,25đ) 0,5
x 3y 3
b) Giải hệ phương trình . 0,75
2x y 4
+ Từ phương trình thứ nhất suy ra x 3y 3 , thay x 3y 3 vào phương trình còn lại ta được: 0,25
2(3y 3) y 4 . Tìm được Câu 3 y 2 . 0,25 (2,5)
Suy ra x 3. Vậy nghiệm của hệ phương trình đã cho (x ; y) (3; 2). 0,25
c) Cho phương trình 2
x 4x 2m 1 0 (1), với m là tham số. Tìm m để phương
trình (1) có hai nghiệm phân biệt 1,0 x , x x x 2 1 2 sao cho . 1 2
+ ' 5 2m 0,25
+ Phương trình (1) có hai nghiệm phân biệt khi 5 ' 0 m 0,25 2 2 2
x x 2 (x x ) 4 (x x ) 4x .x 4 (2) 1 2 1 2 1 2 1 2 0,25 Thay (thỏa). 1 x 2 x 4; 1 x 2 x
2m 1 vào (2) tìm được m 2 0,25 Trang 2
Vậy m 2 là giá trị cần tìm.
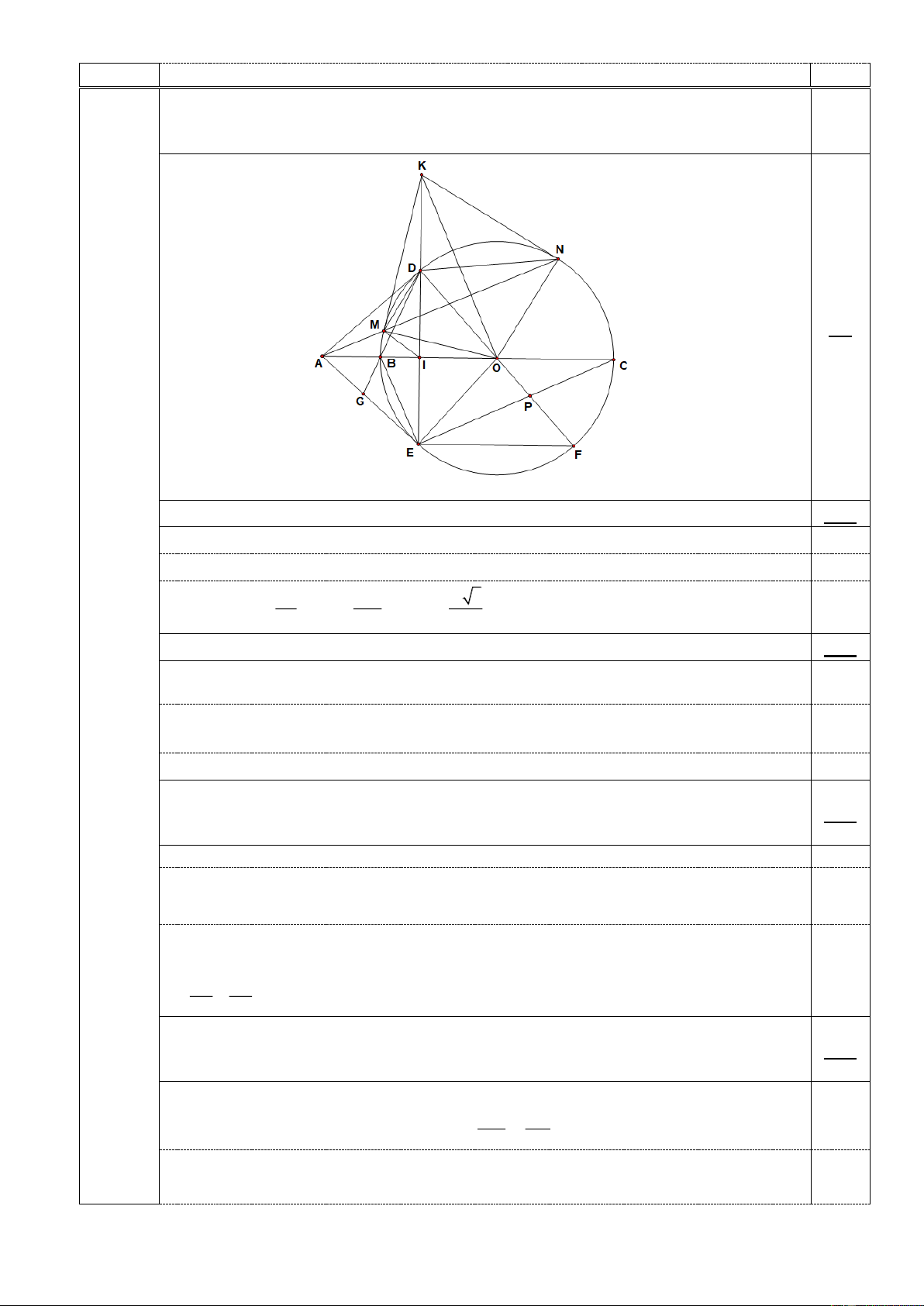
Cho đường tròn (O ; R) có đường kính BC. Trên tia đối của tia BC, lấy điểm A sao
cho BO = 2BA. Vẽ tiếp tuyến AD với đường tròn (O) (D là tiếp điểm) và dây cung
DE của đường tròn (O) vuông góc với BC. 0,5
+ Hình vẽ phục vụ câu a: 0,25 điểm, hình vẽ phục vụ câu b, c: 0,25 điểm
a) Tính độ dài đoạn thẳng AD theo R. 0,75
+ Tam giác OAD vuông tại D. 0,25 Suy ra 2 2 2 AD = OA - OD 0,25 2 2 3R 5R R 5 2 - R = AD = . 0,25 2 4 2 Câu 4
b) Chứng minh AE là tiếp tuyến của đường tròn (O). 0,75 (3,5)
+ Gọi I là giao điểm của OB và DE. 0,25
Tam giác ODE cân tại O có OI là đường cao nên cũng là phân giác.
Xét hai tam giác AOD và AOE có: OD=OE, OA chung, AOD AOE 0,25
Suy ra hai tam giác AOD và AOE bằng nhau. Mà 0 OAD 90 nên 0
OEA 90 . Vậy AE là tiếp tuyến của đường tròn (O). 0,25
c) Vẽ đường kính DF của đường tròn (O). Gọi P là giao điểm của EC và DF, G là
giao điểm của hai đường thẳng BD và AE. Chứng minh BC // EF và PO . GE = PC . 0,75 GB.
+ Lập luận BC và EF cùng vuông góc với DE nên song song với nhau. 0,25
+ Tứ giác BEFD nội tiếp nên GBE EFD 0,25
Mà EFD POC (so le trong) nên GBE POC .
+ BEG OCP (chắn cung BE).
Hai tam giác GBE và POC đồng dạng (g-g) 0,25 GB GE PO.GE = PC.GB PO PC
d) Vẽ cát tuyến AMN của đường tròn (O) (cát tuyến không đi qua O), các tiếp tuyến
tại M và N của đường tròn (O) cắt nhau tại K. Chứng minh ba điểm K, D, E thẳng 0,75 hàng.
+ Chứng minh được hai tam giác AMD và ADN đồng dạng 2 AM.AN=AD . AM AI 0,25 Mà 2
AD AI.AO nên AM.AN AI.AO = . AO AN
Hơn nữa MAI OAN , suy ra hai tam giác AMI và AON đồng dạng. 0,25
AIM ANO . Suy ra tứ giác MION nội tiếp (*) Trang 3
+ Tứ giác KMON nội tiếp đường tròn đường kính KO (**)
Từ (*) và (**) suy ra 5 điểm K, M, I, O, N cùng nằm trên một đường tròn đường 0,25
kính KO nên KI vuông góc với IO.
Mà DE vuông góc với IO nên ba điểm K, D, E thẳng hàng.
* Lưu ý: Thí sinh làm đúng bằng cách khác thì vẫn cho điểm tối đa câu đó. Trang 4