Đề thi tuyển sinh 10 môn toán THPT năm 2023-2024 sở GD Hưng Yên (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT HƯNG YÊN NĂM HỌC 2023 - 2024 Bài thi: TOÁN ĐỀ CHÍNH THỨC
Dành cho thí sinh dự thi các lớp chuyên: Toán, Tin học
Thời gian làm bài: 150 phút, không kể thời gian phát đề x 2 2x  x x  2
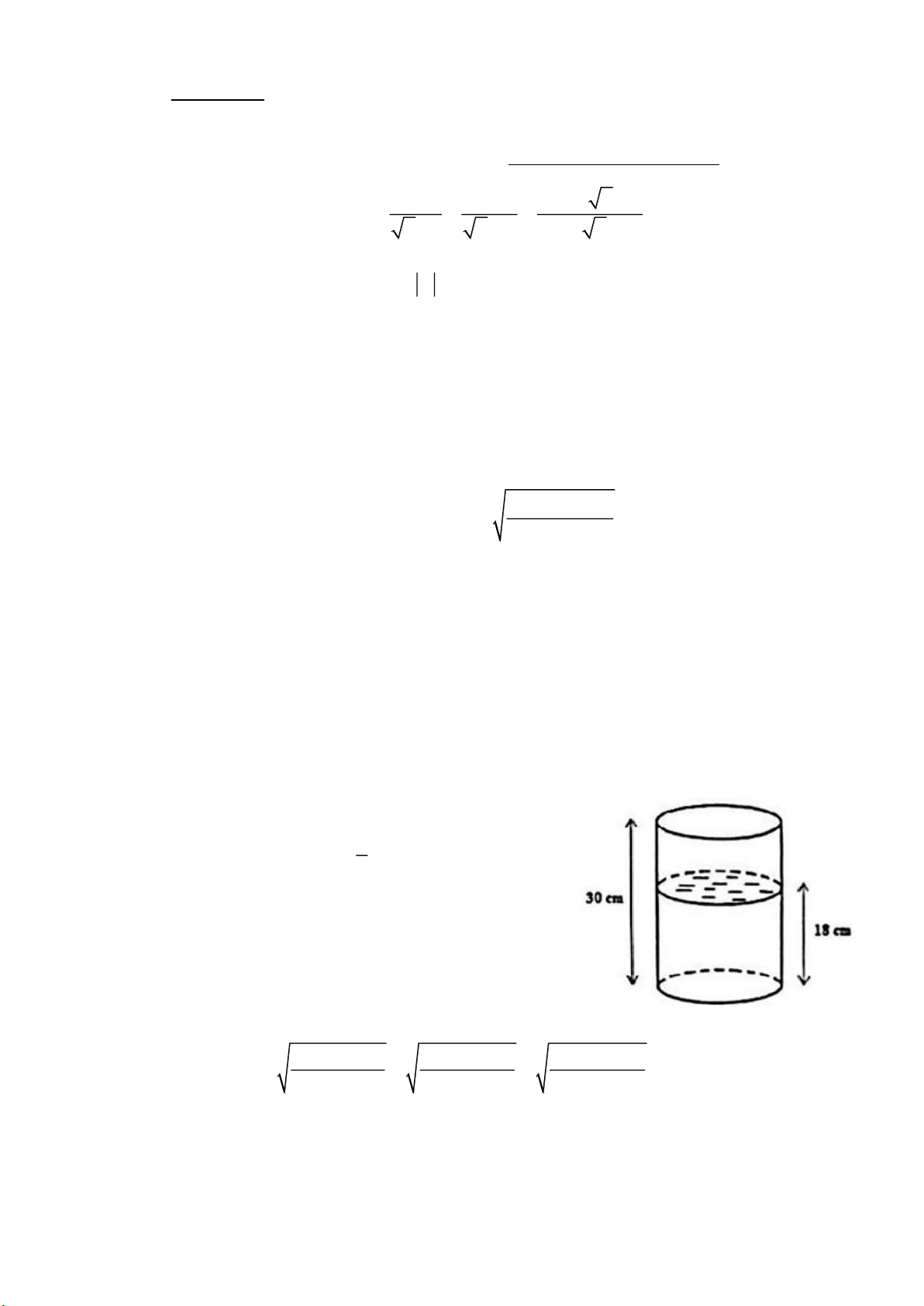
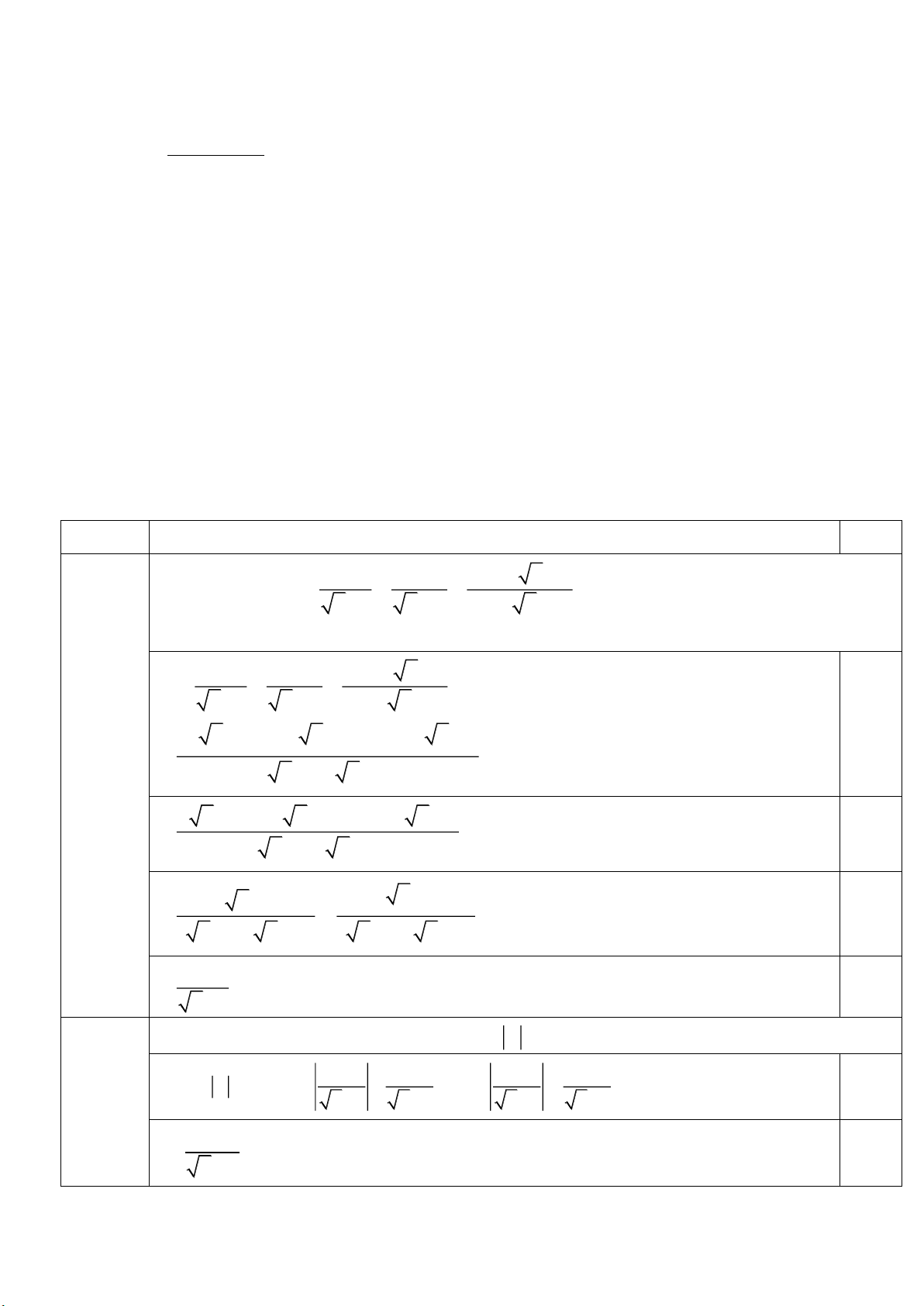
Câu I (2,0 điểm). Cho biểu thức P   
với x  0, x  1, x  4. x 1 x  2 x  3 x  2
a) Rút gọn biểu thức P.
b) Tìm tất cả các giá trị của x để P  P  0.
Câu II (2,0 điểm).
1. Cho parabol  P 2
: y  x và đường thẳng d  : y  m  2 x  m  8 (với m là tham số).
Tìm các giá trị của m để đường thẳng d  cắt parabol  P tại hai điểm phân biệt nằm bên phải
trục tung, có hoành độ x , x thỏa mãn 3 x  x  0 . 1 2 1 2
2. Tìm các nghiệm nguyên  ;
x y của phương trình:  2 2
2024 x  y   20232xy   1  5 .
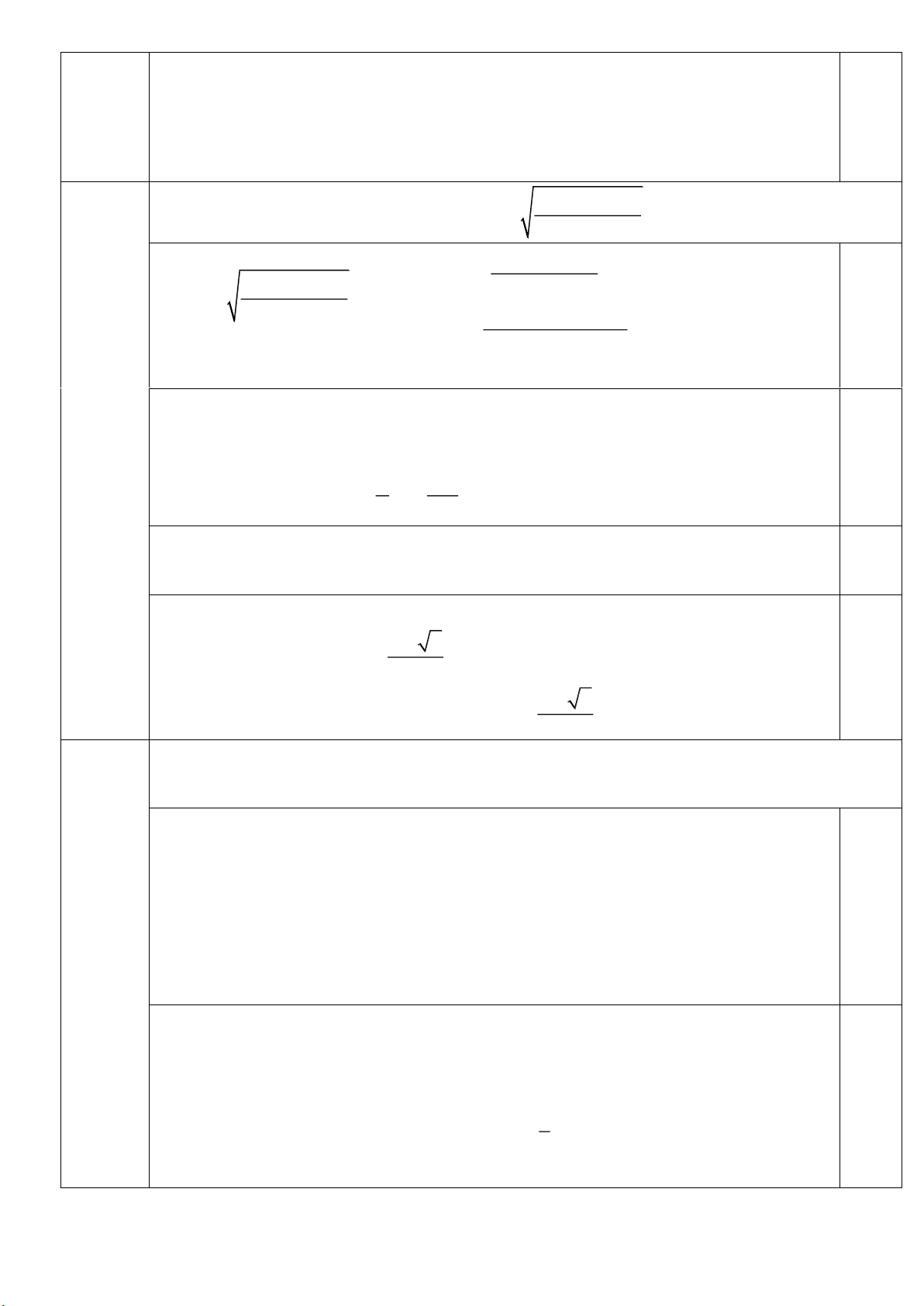
Câu III (2,0 điểm). 2 16x  6x  2
1. Giải phương trình 3 2 3
3x  7x  6x  4  3 . 3 2 2
x  y  x  y  8
2. Giải hệ phương trình  . 2 2
2x  y  3xy  3x  2y 1  0
Câu IV (3,0 điểm).
1. Cho tam giác ABC đều nội tiếp đường tròn  ;
O R , H là trung điểm của cạnh BC .
M là điểm bất kì thuộc đoạn BH ( M khác B ). Lấy điểm N thuộc đoạn CA sao cho
CN  BM . Gọi I là trung điểm của đoạn MN .
a) Chứng minh bốn điểm O, M , H , I cùng thuộc một đường tròn.
b) Chứng minh diện tích tam giác IAB không đổi. Xác định vị trí của điểm M để đoạn
thẳng MN có độ dài nhỏ nhất.
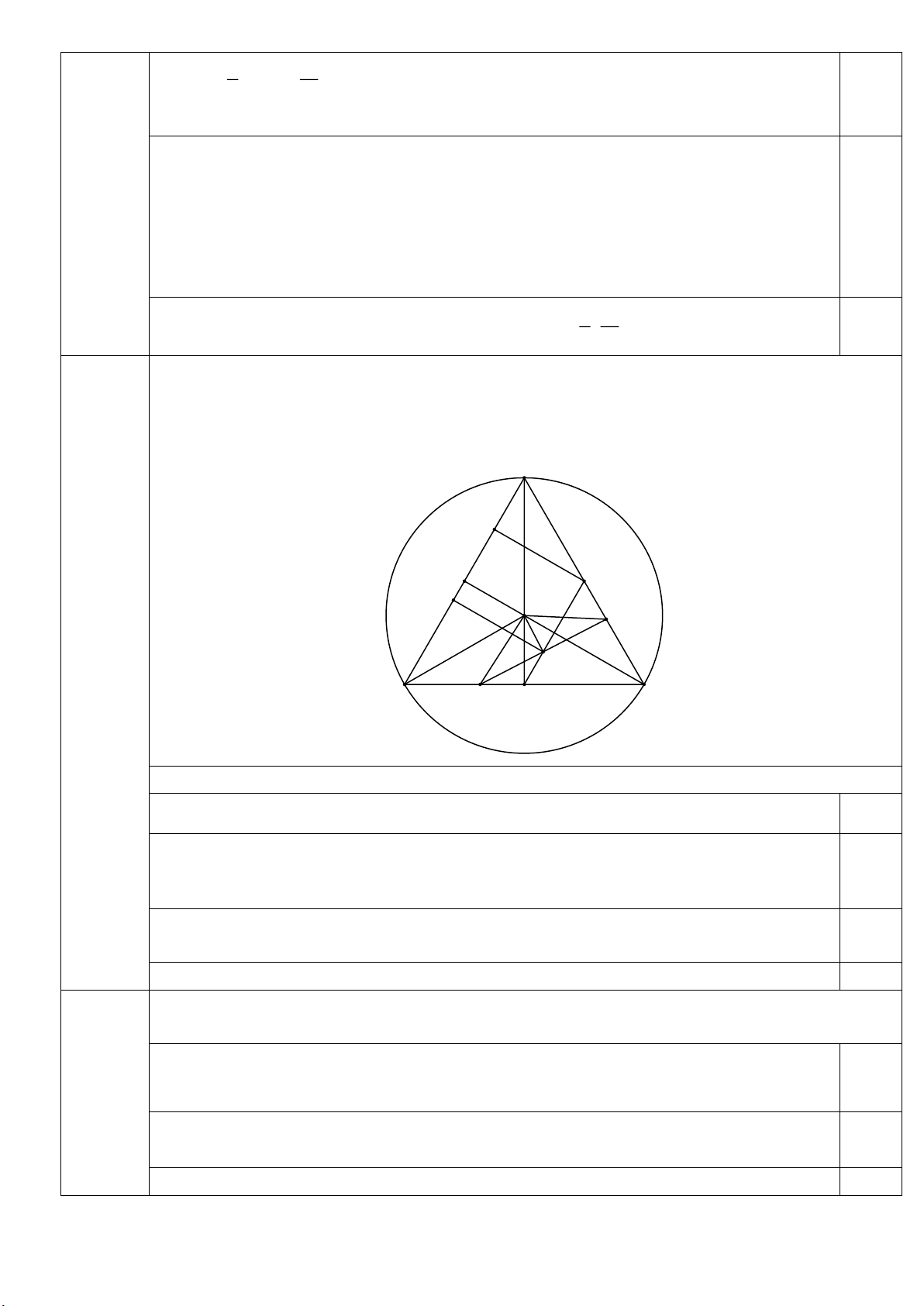
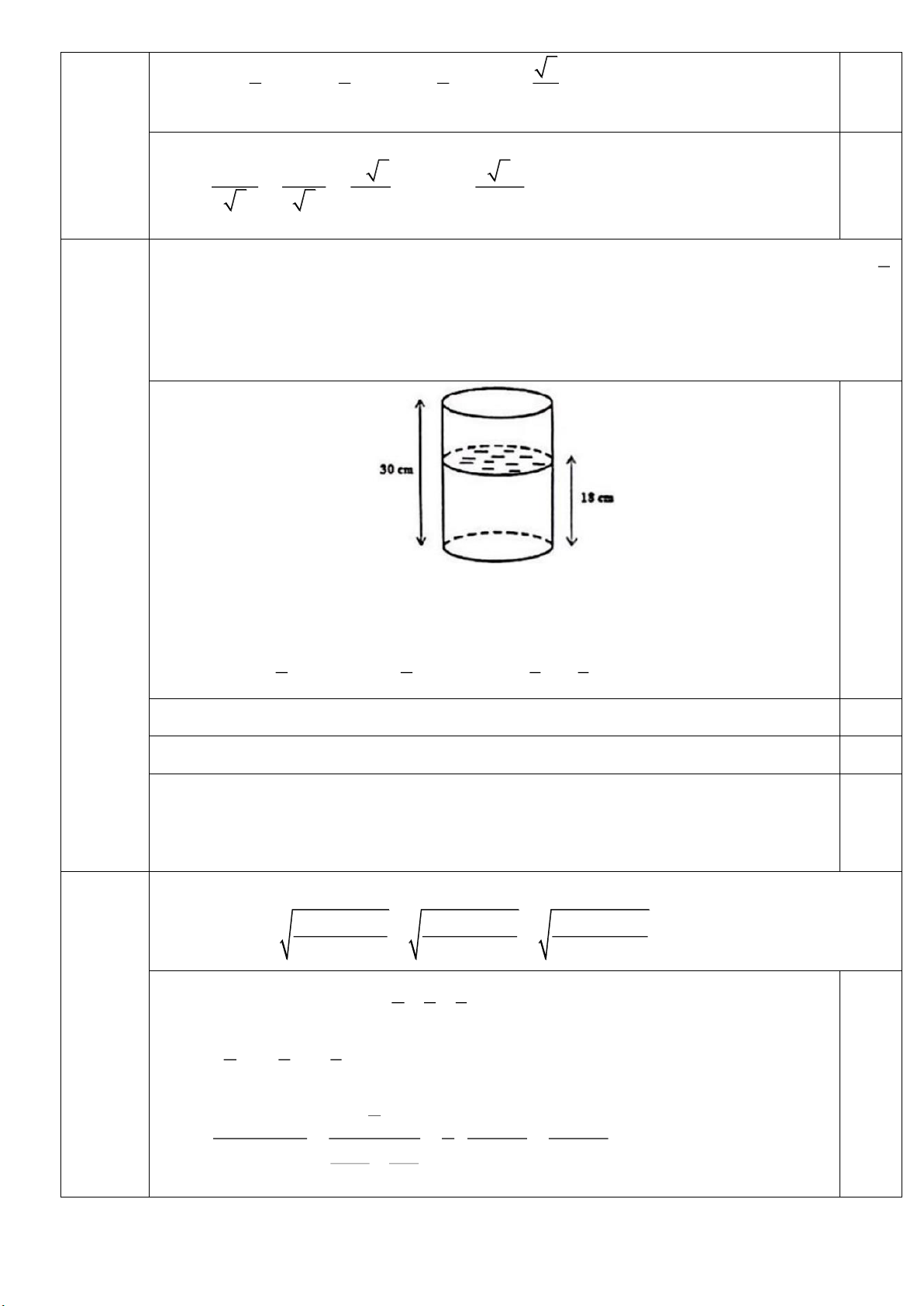
2. Có một bình thủy tinh hình trụ cao 30cm chứa nướ 1
c, diện tích đáy bình bằng diện tích xung quanh, 6
mặt nước cách đáy bình là 18cm (hình vẽ bên). Cần đổ
thêm bao nhiêu lít nước nữa để nước vừa đầy bình (Bỏ qua
bề dày của bình, cho   3,14 và lấy kết quả làm tròn đến
chữ số thập phân thứ nhất)
Câu V (1,0 điểm). Cho ba số thực dương a, ,
b c thỏa mãn ab  bc  ca  3abc . Tìm giá trị lớn a b c
nhất của biểu thức T    . 2 2 2 2 2 2 3b c  abc 3a c  abc 3a b  abc
------------ HẾT ------------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh.......................................................... Phòng thi số:……...............................................
Số báo danh:...............................................................
Chữ ký của Cán bộ coi thị: ................................ Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HƯNG YÊN
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2023 - 2024
(Hướng dẫn chấm gồm 06 trang) Môn thi: TOÁN
Dành cho thí sinh dự thi các lớp chuyên: Toán, Tin học
I. Hướng dẫn chung
1) Hướng dẫn chấm chỉ trình bày các bước chính của lời giải hoặc nêu kết quả. Trong bài
làm, thí sinh phải trình bày lập luận đầy đủ.
2) Nếu thí sinh làm bài không theo cách nêu trong đáp án mà vẫn đúng thì cho đủ điểm từng
phần như hướng dẫn quy định.
3) Việc chi tiết hoá thang điểm (nếu có) phải đảm bảo không làm thay đổi tổng số điểm của
mỗi câu, mỗi ý trong hướng dẫn chấm và được thống nhất trong Hội đồng chấm thi. Các điểm
thành phần và điểm cộng toàn bài phải giữ nguyên không được làm tròn.
II. Đáp án và thang điểm Câu Nội dung Điểm Câu I.1 x 2 2x  x x  2
Cho biểu thức P   
với x  0, x  1, x  4.
1.0 điểm x 1 x  2 x  3 x  2
a) Rút gọn biểu thức P. x 2 2x  x x  2 P    x 1 x  2 x  3 x  2
x  x  2  2 x  
1  2x  x x  2 0,25 
 x  1 x 2
x x  2x  2 x  2  2x  x x  2   0,25 x   1  x  2 2  x   x 2 2 4     0,25 x  
1  x  2  x   1  x  2 2  0,25 x 1 Câu I.2
b) Tìm tất cả các giá trị của x để P  P  0.
1.0 điểm 2 2 2 2 0,25
Ta có P  P  0    0   x 1 x 1 x 1 x 1 2 Þ > 0,25 0 x - 1 Trang 2
 x 1  0  x  1 0,25
Kết hợp với điều kiện suy ra x  1; x  4. 0,25    
Câu II.1 1. Cho parabol  P 2
: y  x và đường thẳng d  : y m 2 x m 8 (với m là tham
1.0 điểm số). Tìm các giá trị của m để đường thẳng d  cắt parabol  P  tại hai điểm phân biệt
nằm bên phải trục tung, có hoành độ x , x thỏa mãn 3
x  x  0 . 1 2 1 2
+ Xét phương trình hoành độ giao điểm 2
x  m  2 x  m  8  0
+ Để thỏa mãn yêu cầu bài toán thì phương trình (1) phải có 2 nghiệm dương phân biệt. 2
Ta có:   m    m   2 2 2 4
8  m  4m  4  4m  32  m  28   0 
Phương trình (1) có 2 nghiệm dương phân biệt khi S  0 0,25 P  0  2 m  28  0 
 m  2  0  m  2 7 . m 8  0  + Theo đề bài ta có:
x  x  0  x  x  x  x .x  m  8  x  m  8  x  m  83 3 3 4 4 4 1 2 1 2 1 1 2 1 2 0,25
Do đó x  x  m  2  m  8  m  83 4 4  m  8  6. 1 2
+ Đặt 4 m  8  t t  0, ta có: 0,25 3 4
t  t  t   t   3 2 6
2 t  t  2t  3  0  t  2 (vì 3 2
t  0  t  t  2t  3  0 )
4 m  8  2  m  8 (thỏa mãn). Vậy m  8 0,25 2 2
Câu II.2 2. Tìm các nghiệm nguyên  ;
x y của phương trình: 2024 x  y   20232xy   1  5 .
1,0 điểm 2024 2 2
x  y   20232xy   1  5
 2023x  y2 2 2
 x  y  2028   1 
x  y2 
 x  y2 2028 2023 2028 
 0  x  y2  1 0  x  y  1 0,25 2023  x  y  0
  x y 1 
Nếu x  y  0  x  y . Từ (1) 2 2
 2x  2028  x 1014 (vô nghiệm nguyên) 0,25 x  y  1   y  x 1
Nếu x  y  1 thì    và từ (1) 2 2
 x  y  5 2 x  y  1  y  x 1
Thay y  x 1 vào (2) ta được x   x  2 2 2 1
 5  x  x  2  0 0,25 x  1   y  2    (thỏa mãn)
x  2  y  1 Trang 3
Thay y  x  1 vào (2) ta được x   x  2 2 2 1
 5  x  x  2  0
x  1 y  2   (thỏa mãn) 0,25 x  2   y  1 
Vậy có 4 cặp số nguyên  ;
x y thỏa mãn là  1  ; 2  ;2;  1 ;1;2; 2  ;  1 2 Câu III 16x  6x  2
1. Giải phương trình 3 2 3
3x  7x  6x  4  3 .
1,0 điểm 3 2    16x 6x 2 3 y     1 2 16x  6x  2  3 Đặt 3 y  . Ta có hệ  . 3 3 2 
3x  7x  6x  4 y  2 0,25  3
Cộng từng vế (1) với (2) ta được 3 3 2
y  y  x  3x  4x  2
 y  y  x  3 3 1   x   1 3
Đặt a  x 1. Từ (3) có 3 3
y  y  a  a  a  y  2 2
a  ay  y   1  0 0,25 2 2  a  3y Do 2 2
a  ay  y 1  a   1  0  
nên y  a hay y  x  1  y  4
Thay vào phương trình (2) ta được 3 2
x  x  x    x   2 3 7 3 1 0
1 3x  4x   1  0 0,25 x  1 x 1  0      . 2 2 7 3x 4x 1 0     x   3 0,25 2  7
Vậy phương trình đã cho có nghiệm x  1; x  . 3 2 2 Câu III.2
x  y  x  y  8
2. Giải hệ phương trình  . 2 2        1,0 điểm 2x y 3xy 3x 2 y 1 0 Ta có:     2
x  xy    2 2 2 2
xy  y    x  y  2x  y 1  0
 2x  y  
1  x  y   1  0
2x  y 1  0   0,25
x  y 1  0
 y  2x 1
 y  x1
Thay y  2x  1 vào (1) ta được: 2 2
x   x   2 2
1  x  2x 1  8  5x  7x  6  0 3  169  0 0,25  3 x 
Phương trình (3) có hai nghiệm phân biệt  5  x  2  Trang 4 3 11 Với x   y  5 5 Với x  2   y  3
Thay y  x  1 vào (1) ta được: 2 2
x   x   2
1  x  x 1  8  2x  4x  6  0 4 Vì 2  4   6
   0 nên phương trình (4) có hai nghiệm phân biệt x 1; x  3  0,25
Với x  1  y  2 Với x  3   y  2  3 11 Vậy nghiệm  ;
x y của hệ phương trình đã cho là: ; ; 2  ; 3  ;1;2; 3  ; 2     0,25  5 5 
Câu IV.a 1. Cho tam giác ABC đều nội tiếp đường tròn  ;
O R , H là trung điểm của cạnh BC
. M là điểm bất kì thuộc đoạn BH ( M khác B ). Lấy điểm N thuộc đoạn CA sao cho
1,0 điểm CN  BM . Gọi I là trung điểm của đoạn MN . A Q E K P O N I C B M H
a) Chứng minh bốn điểm O, M , H , I cùng thuộc một đường tròn. Do ABC 
đều nên OH  BC hay OH  MH   1 0,25 Xét B  OM và C
 ON có BM  CN gt 0
,OB  OC  R,OBM  OCN  30 (do 0,25 ABC  đều) B  OM  C  ON  . c g.c .
OM  ON hay O
 MN cân tại O 0,25
Do I là trung điểm của MN suy ra OI ^ MN hay OI ^ MI ( ) 2
Từ (1) và (2) suy ra OMHI nội tiếp  O, M , H , I cùng thuộc một đường tròn 0,25
Câu IV.b b) Chứng minh diện tích tam giác IAB không đổi. Xác định vị trí của điểm M để
đoạn thẳng MN có độ dài nhỏ nhất.
1,0 điểm Ta có 0
180 = OMB + OMC = ONC + OMC Þ tứ giác OMCN nội tiếp (tổng hai 0,25 góc đối bằng 1800) nên 0 0 0
MON = 180 - NCM = 120 Þ OMN = 30 Ta có 0 0
OHI = OMN = 30 Þ IHC = 60 Þ IHC = ABC Þ HI / / AB 0,25
Gọi K là trung điểm của AC thì H , I , K thẳng hàng.
Kẻ IP,CE, KQ lần lượt vuông góc với AB 0,25 Trang 5 1 1 1 3 Thì 2 S = I . P AB = . KQ AB = CE.AB = AB không đổi. IAB 2 2 4 8
Vậy diện tích DIAB không đổi (đpcm)
Trong tam giác vuông OMI và OMH có: 2OM 2OH R 3 2 3R IM = ³ = Þ MN ³ 0,25 3 3 3 3
Dấu “=” xảy ra Û M º H. Câu V 1
2. Có một bình thủy tinh hình trụ cao 30cm chứa nước, diện tích đáy bình bằng 6
1,0 điểm diện tích xung quanh, mặt nước cách đáy bình là 18cm (hình vẽ bên). Cần đổ thêm
bao nhiêu lít nước nữa để nước vừa đầy bình (Bỏ qua bề dày của bình, cho   3,14
và lấy kết quả làm tròn đến chữ số thập phân thứ nhất) 0,25
Gọi chiều cao và bán kính đáy của bình lần lượt là , h R (cm).
Thể tích của bình, thể tích nước có trong bình và thể tích nước cần đổ đầy bình lần
lượt là V ,V ,V . 1 2 1 1 1 1 Ta có: 2 S = S Û R  = .2 Rh  Û R = h = .30 = 10 đáy cm xq ( ) 6 6 3 3 Thể tích của bình là 2 2 V = R  h =  = ( 3 .10 .30 3000 cm ) 0,25
Thể tích nước có trong bình là 2 2 V = R  .18 = .1  0 .18 = 1800( 3 cm 0,25 1 )
Vậy thể tích nước cần đổ thêm vào để đầy bình là:
V = V - V = 3000 - 1800 = 1200 = 1200.3,14 = 3768( 3 cm Þ V » 3,8 l 2 1 ) 2 ( ) 0,25
Vậy cần đổ thêm 3,8 lít nước thì bình đầy nước.
Câu VI Cho ba số thực dương a, ,
b c thỏa mãn ab  bc  ca  3abc . Tìm giá trị lớn nhất của
1,0 điểm a b c
biểu thức T    . 2 2 2 2 2 2 3b c  abc 3a c  abc 3a b  abc 1 1 1
Ta có ab  bc  ca  3abc     3 a b c 1 1 1
Đặt x  , y  , z 
 x  y  z  3. a b c 0,25 1 2 2 a 1 3x  yz y z Ta có: x   :  2 2 2 2 3b c  abc 3 1 x xy z 3x  yz  2 2 y z xyz Trang 6 2 2 a y z 1 1    yz  yz 2 2 3b c  abc 3x  yz 3x  yz
x  y  zx  yz 1
 yz x yx z b 1 c 1 Tương tự:  xz ;  xy 2 2 3a c  abc
 y  x y  z  2 2 3a b  abc
z  xz  y 
Áp dụng bất đẳng thức Cauchy cho hai số dương ta có: 1 1 1 1  1 1       
x  y  x  z .
x  y x  z 2  x  y x  z  0,25 1 yz  1 1   yz     
x  y  x  z 2  x  y x  z 
Chứng minh tương tự ta có: 1 xy  1 1  xy     
z  x z  y 2  z  x z  y  1 xz  1 1  0,25 xz     
y  x y  z 2  y  x y  z  1 3
Do đó T   x  y  z  2 2  1 1 
 x  y x  z   1 1  
Dấu bằng xảy ra khi và chỉ khi  y  x y  z  1 1    z  x z  y 0,25
x  y  z  3
 x  y  z 1 a  b  c 1 nên 3
Vậy giá trị lớn nhất của biểu thức T là
khi và chỉ khi a  b  c  1 2
------------ HẾT ------------ Trang 7