



Preview text:
SỞ GD & ĐT HOÀ BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10
TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 2022 - 2023
ĐỀ CHÍNH THỨC ĐỀ THI MÔN TOÁN
(DÀNH CHO TẤT CẢ CÁC THÍ SINH)
Ngày thi: 05 tháng 6 năm 2022
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
(Đề thi gồm có 01 trang, 04 câu)
------------------------------------------------------------------------------------------------------------------
Câu I (3,0 điểm)
1) Rút gọn các biểu thức sau: 2 a) A 5 20 b) B 3 1
2) Tìm m để đồ thị hàm số y (m 2)x 3 đi qua điểm ( A 2;3) . 3) Cho phương trình 2
x 4x 2m 1 0 (m là tham số).
a) Giải phương trình với m 2
b) Tìm m để phương trình có nghiệm.
Câu II (3,0 điểm)
1) Một ô tô đi từ A và dự định đến B lúc 11 giờ trưa. Nếu xe chạy với vận tốc
40km/h thì sẽ đến B chậm 1 giờ so với dự định. Nếu xe chạy với vận tốc 50 km/h thì sẽ
đến B sớm 24 phút so với dự định. Tính độ dài quãng đường AB và thời điểm dự định
xuất phát của ô tô tại A.
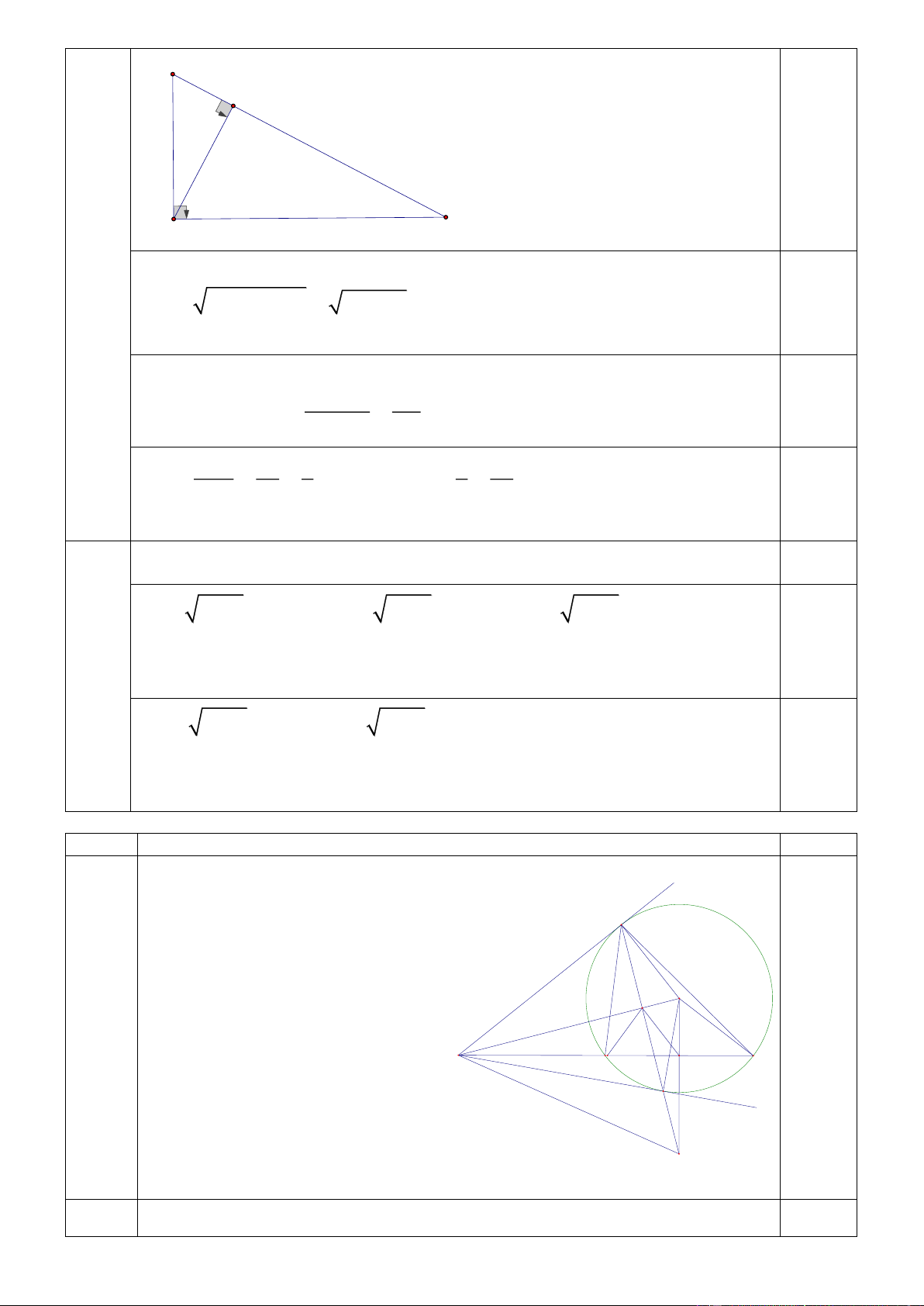
2) Cho tam giác ABC vuông tại A, đường cao AH, biết AB 6cm , AC 8cm . Tính độ dài AH, BH, CH.
3) Giải hệ phương trình: x y 2 5
2x y 11
Câu III (3,0 điểm)
Cho đường tròn (O), một đường thẳng d không đi qua tâm O cắt đường tròn (O)
tại 2 điểm phân biệt M và N. Lấy điểm A tùy ý thuộc d và nằm ngoài đường tròn (O) (
AM AN ). Qua A vẽ hai tiếp tuyến AB và AC của đường tròn (O) (B và C là các tiếp
điểm). Gọi D là giao điểm của AO và BC.
1) Chứng minh rằng: Tứ giác OBAC là tứ giác nội tiếp. 2) Chứng minh rằng: 2
AB AM .AN
3) Chứng minh rằng: ADM ANO .
4) Chứng minh rằng khi A thay đổi (A thuộc d và nằm ngoài đường tròn (O),
AM AN ) thì đường thẳng BC luôn đi qua một điểm cố định.
Câu IV (1,0 điểm)
2x 3y 8z 9
1) Cho các số thực không âm x, y, z thỏa mãn:
4x y 12z 17
Chứng minh rằng: 25 5x 2y 26z 35
2) Cho các số thực a, , b c thỏa mãn: 2 2 2
a b c 2022. Tìm giá trị nhỏ nhất của
biểu thức: P ab 2bc ac -------- Hết --------
Họ và tên thí sinh: ............................................. Số báo danh: ......................... Phòng thi: .......
Giám thị 1: .................................................... Giám thị 2: ........................................................... SỞ GD & ĐT HOÀ BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 Trang 1
TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 2022-2023
HƯỚNG DẪN CHẤM MÔN TOÁN
(DÀNH CHO TẤT CẢ CÁC THÍ SINH
(Hướng dẫn chấm này gồm có 04 trang)
Câu I (3,0 điểm) Phần Nội dung Điểm
a) Rút gọn biểu thức: A =
5 20 5 2 5 3 5 0,5 1 2 2( 3 1) 0,5 b) B 3 1 3 1 3 1 2
(d) : y (m 2)x 3 đi qua điểm A(-2;3) khi (m 2)( 2 ) 3 3 0,5 (m 2)( 2
) 3 3 m 5 0,5 3
a) Với m = 2 ta có phương trình 2
x 4x 3 0
Ta có a+b+c = 1+(-4) +3 = 0 nên phương trình có hai nghiệm 0,5 x 1; x 3 1 2
b) Ta có ' 4 2m 1 5 2m 0,25 5
Phương trình có nghiệm khi và chỉ khi 5 2m 0 m 2 0,25 Vậy...
Câu II (3,0 điểm) Phần Nội dung Điểm
Gọi quãng đường AB có độ dài là x(km) ; x > 0 2 0,25 Đổi 24 phút = (h) 5 x
Khi ô tô đi với vận tốc 40km/h thì thời gian để đến B là (h) 40 0,25 x
Khi ô tô đi với vận tốc 50 (km/h) thì thời gian để đến B là (h) 50 1
Theo bài ra ta có phương trình: x x 2 1
5x 200 4x 80 x 280 0,25 40 50 5
Vậy quãng đường AB có độ dai là 280 (km)
Thời gian dự định là 6 (h)
Thời điểm xuất phát khi dự định là 5 giờ sáng. 0,25 Trang 2 B H A C
Áp dụng định lý Pitago trong tam giác ABC ( vuông tại A) ta có 2 2 2 BC
AB AC 36 64 10 . 0,25
Ta có AH. BC = AB.AC ( hệ thức giữa cạnh và đường cao trong tam giác ABC A . B AC 6.8 vuông tại A) 0,25 AH 4,8(cm) ; BC 10 BC 10 5 5 75 BH (cm);CH 10 (cm) 2 AB 36 8 8 8 0,5
Điều kiện: y 2 0,25
x y 2 5
2x 2 y 2 10
y 2 y 2 1 0,25
2x y 11
2x y 11
2x y 11 3 2 (
y 2 1) 0 y 2 1 y 3 0,5
2x y 11
2x y 11 x 4
Vậy hệ phương trình có nghiệm là (x;y ) = (4;3)
Câu III (3,0 điểm) Phần Nội dung Điểm B O D A M I N C K 1 Ta có B OA = 900 ; A
CO = 900 ( tính chất tiếp tuyến); 0,5 Trang 3 Suy ra O BA+ A CO = 1800 0,5
Vậy tứ giác ABOC nội tiếp đường tròn đường kính AO
Xét hai tam giác ABM và ANB có A chung; ABM = A
NB ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và 0,5
góc nội tiếp chắn cung BM). 2 A BM A NB(g g) AB AM Vậy 2
AB AM.AN 0,5 AN AB 2 2 Ta có A .
D AO AB ; AM.AN AB A .
D AO AM.AN 0,25 3 AD AN Xét A NO và A DM có A chung; ( chứng minh trên ) AM AO 0,25 A DM A
NO(c g c) A DM A NO(dpcm) 4
Gọi I là trung điểm của MN, OI cắt BC tại K.
Ta có tứ giác ADIK nội tiếp đường tròn đường kính AK. 0,25
Suy ra : OI.OK O . D OA 2 R 2 2
OI.OK OB R OK OI 0,25
Do OI không đổi nên OK không đổi, chứng tỏ BC luôn đi qua điểm K cố định khi A thay đổi
Câu IV (1,0 điểm) Phần Nội dung Điểm Theo đầu bài ta có:
2x 3y 8z 9
2x 3y 8z 9
4x 6y 16z 18 0,25
4x y 12z 17
4x y 12 z 17
4x y 12 z 17 5 z 7
y 28z 35 y 4 z 5 0 4 5 z 4x y 12 z 17 x 2 z 3 0 3 4 1 z 2
Ta có 25x 2 y 26z 5( 2 z 3) 2( 4
z 5) 26z 25 8z 5 0,25 Vi 0 z
nên 25 25 8z 35(dpc ) m 4 Trang 4
Ta có: a b c 2 2 2 2
a b c 2(ab bc ca) 0 2 2 2 (
a b c ) 2 022
ab bc ca 1011 2 2 0,25
Ta lại có : b c 2 2 2
b c 2bc 0 2 2 2 2 2 ( b c ) (
a b c ) 2 022 bc 1011 2 2 2 Suy ra: P 2022 2 2 2 0,25
a b c 2022 2 2 b 1011 b 1011
a b c 0 Dấu = xảy ra khi b c c 1011 b c 0 a 0 a 0 a 0 b 1011 Hoặc c 1011 a 0 Vậy P 2022 min
* Chú ý: Các lời giải đúng khác đều được xem xét cho điểm tương ứng. Trang 5




