Đề thi tuyển sinh 10 THPT chuyên năm 2023-2024 môn toán Sở GD Bắc Ninh (có đáp án và lời giải chi tiết)
Tổng hợp Đề thi tuyển sinh 10 THPT chuyên năm 2023-2024 môn toán Sở GD Bắc Ninh (có đáp án và lời giải chi tiết) rất hay và bổ ích. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
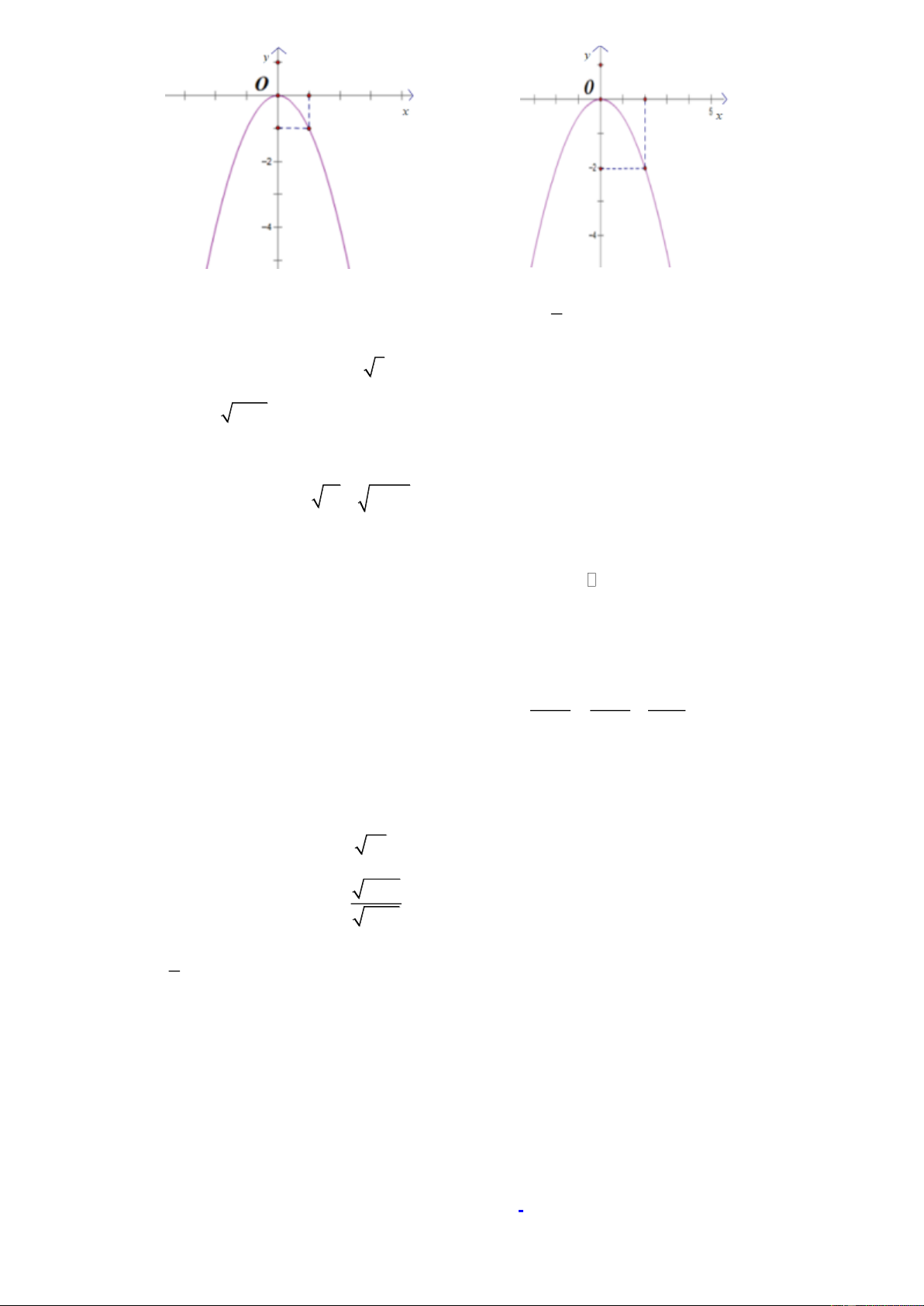
Preview text:
SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 BẮC NINH
NĂM HỌC: 2023 – 2024 Môn: TOÁN
Khoá thi ngày: 6/6/2023
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
I. Trắc nghiệm (4 điểm) Câu 1.
Trong hình vẽ dưới dây cho AOB 100 ; Ax là tiếp tuyến của O tại A . A x B 100° O Số đo xAB bằng A. 100 . B. 130 . C. 120 . D. 50 .
2x y 3 Câu 2. Hệ phương trình có nghiệm là x y 3 A. 2 ;1 . B. 2 ;1 . C. 2 ; 1 . D. 2; 1 . Câu 3.
Cho tam giác ABC vuông tại A , AB 3, BC 6 . Số đo của ACB bằng A. 90 . B. 45. C. 60 . D. 30 . Câu 4.
Căn bậc hai số học của 25 là A. 5 ;5 . B. 5 . C. 5 . D. 5 .
Câu 5 . Hình nào dưới đây là đồ thị của hàm số 2 y x ? A. B. Trang 1 C. D. 3 Câu 6.
Cho tam giác ABC vuông tại A , AC 6 cm , tan B
. Độ dài cạnh BC bằng 4 A. 9 cm . B. 6 3 cm . C. 8 cm . D. 10 cm .
Câu 7 . Biểu thức 3 x có điều kiện xác định là A. x 3.
B. x 3.
C. x 3. D. x 3.
Câu 8 . Kết quả của phép tính 2 2 3 ( 3 ) bằng A. 6 . B. 18 . C. 6 . D. 0 . Câu 9.
Hàm số y (m 5)x 2 (với m là tham số) đồng biến trên khi và chỉ khi A. m 5 . B. m 5 . C. m 7 . D. m 7 . Câu 10. Cho M
NP vuông tại M , đường cao MK . Hệ thức nào sau đây là sai? 1 1 1
A. MK.KP MN.MP . B. . 2 2 2 MK MN MP C. 2 MN N . P NK . D. 2
MK NK.KP .
Câu 11 . Cho ABC
vuông tại A , đường cao AH 6c ,
m BH 4cm . Độ dài cạnh BC bằng: A. 10cm. B. 52cm . C. 9cm . D. 13cm . 7 x
Câu 12 . Khi x 2
, biểu thức M có giá trị bằng: x 3 9 A. . B. 3 . C. 9 . D. 3 . 2
Câu 13 . Hộp sữa có dạng hình trụ với đường kính đáy là 12 cm , chiều cao của hộp sữa là 18 cm . Thể
tích của hộp sữa bằng A. 3 648 cm B. 3 432 cm C. 3 216 cm D. 3 2592 cm x y 3
Câu 14. Hệ phương trình
(với m là tham số) có nghiệm x ; y thỏa mãn x 2y khi 0 0
mx y 3 0 0 A. m 4 . B. m 2 . C. m 5 . D. m 3 .
Câu 15. Cặp số nào sau đây là nghiệm của phương trình 2x y 1? Trang 2 A. 2; 2 . B. 1 ;3. C. 1 ; 3 . D. 2 ; 2 . 3
Câu 16. Hệ số góc của đường thẳng y x là 2 3 A. 2 . B. . C. 1. D. 2 . 2
Câu 17 . Trong các hệ phương trình sau, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
xy 3x 1
x 2y 1 A. . B. .
y 2x 1 2
x 2y 1 x y 3 2 x 3y 1 C. . D. . 2x y 1
x 2y 1 Câu 18. Cho parabol 2
y x cắt đường thẳng y 3
x 4 tại hai điểm phân biệt có hoành độ
x x (x x ). Giá trị của biểu thức T 2x 3x bằng 1, 2 1 2 1 2 A. 5 – . B. 10 – . C. 10 . D. 5 .
Câu 19. Giao điểm của đồ thị hai hàm số y x 1 và y 2x 4 là A. N 1 ;1 . B. M 1;0. C. P 1 ;2. D. Q 3 ; 4 . 3
Câu 20. Cho tam giác ABC vuông tại A , đường cao AH . Cho biết CH 6cmvà sin B . Độ dài 2
đường cao AH bằng A. 2cm. B. 4cm. C. 4 3cm . D. 2 3cm . Câu 21. Cho hàm số 2
y ax (với a 0 là tham số). Điểm E(1; 2) thuộc đồ thị hàm số khi 1 1 A. a 2 . B. a . C. a 2 . D. . 4 4
Câu 22. Đường thẳng nào dưới đây song song với đường thẳng y 2 x 1?
A. y 2x 1.
B. y 6 2x 1 .
C. y 2x 1.
D. y 1 2x .
2x y 7
Câu 23. Biết x ; y là nghiệm của hệ phương trình:
. Giá trị của biểu thức 2 2 x y bằng o o x y 2 o o A. 8 . B. 5 . C. 10 . D. 7 .
Câu 24. Cho thể tích V của một hình nón có diện tích đáy S 6 2
cm và chiều cao h 3cm là A.V 9 3 cm .
B. V 6 3 cm .
C. V 3 3 cm .
D. V 18 3 cm .
x 2y 3
Câu 25. Hệ phương trình
(với m là tham số) vô nghiệm khi
2x my 1 A. m 2 . B. m 4 . C. m 1. D. m 4 . Trang 3
Câu 26. Biểu thức 2 3 2x bằng A. 2x 3 . B. 2x 3 . C. 3 2x .
D. 2x 3 và 3 2x
Câu 27. Đường thẳng y 2x 3 đi qua điểm nào sau đây A. N 1 ;1 . B. Q 1 ; 1 . C. M 1; 1 .
D. P 1; 1 . ax 3y 4
Câu 28. Cho hệ phương trình
( với a;b là tham số). Với giá trị nào của a;b thì hệ phương
x by 2
trình đã cho có nghiệm 1 ;2 ? a 2 a 2 a 2 a 2 A. . B. 1 . C. 1 . D. 1 . b 0 b b b 2 2 2
mx y 3
Câu 29. Cho hệ phương trình
(với m là tham số). Số các giá trị nguyên của m để hệ 3
x my 4
phương trình đã cho có nghiệm duy nhất ;
x y thỏa mãn x 0, y 0 là A. 5 . B. 2 . C. 4 . D. 3 .
Câu 30 . Trong mặt phẳng tọa độ Oxy,đồ thị hàm số y mx 2 (với m 0 là tham số) cắt các trục
Ox, Oy lần lượt tại ,
A B .Có bao nhiêu giá trị của m để diện tích tam giác OAB bằng 3 ? A. 3. B.1. C. 2 . D. 0 .
Câu 31. Cho ba đường thẳng đôi một phân biệt y x 2d ; y 2x 1d ; y 2 m
1 x md 3 2 1
(với m là tham số). Giá trị của m để ba đường thẳng nói trên cùng đi qua một điểm là A. m 2 ;1 . B. m 1. C. m 2 . D. m 3 . 2 y 1 3 x 2
Câu 32. Hệ phương trình
có nghiệm x ; y thì x y bằng 0 0 1 0 0 3 y 1 2 x 2 A. 1. B. 2 . C. 2 . D. 1.
II. Tự luận (6 điểm) Câu 1. (1,0 điểm) x Rút gọn biểu thưc sau 1 1 1 A :
với x 0; x 4 x 2 x 2 4 x x 2 Câu 2. (1,5 điểm) Cho phương trình 2
x 2m
1 x m 3 0 (1) ( m là tham số).
1. Giải phương trình (1) khi m 0 . Trang 4
2. Tìm giá trị của m để phương trình (1) có hai nghiệm đối nhau. Câu 3. (1,0 điểm)
Một phòng họp có 165 ghế ngồi được xếp thành các hàng, mỗi hàng có số ghế bằng nhau.
Trong một buổi họp có 208 người đến dự họp, do đó ban tổ chức đã kê thêm 1 hàng ghế và
mỗi hàng ghế phải nhiều hơn quy định 2 hàng ghế mới đủ chỗ ngồi. Hỏi lúc đầu mỗi phòng
họp có bao nhiêu hàng ghế, mỗi hàng ghế có bao nhiêu ghế? Câu 4. (2,0 điểm)
Cho đường tròn tâm O đường kính BC . Trên đường tròn đã cho lấy điểm A cố định ( A khác
B và C ) và lấy điểm D thay đổi trên cung nhỏ AC ( D khác A và C ). Kẻ AH vuông góc
với BC ( H thuộc BC ). Hai đường thẳng BD và AH cắt nhau tại I .
1. Chứng minh tứ giác IHCD nội tiếp. 2. Chứng minh rằng 2
AB BI.B . D
3. Lấy điểm M trên đoạn thẳng BC sao cho BM AB . Chứng minh rằng tâm đường tròn
ngoại tiếp tam giác MID luôn nằm trên một đường thẳng cố định khi D thay đổi trên cung nhỏ AC . Câu 5. (0,5 điểm) Cho các số không âm ,
x y, z thỏa mãn điều kiện 2 2
x y 8x 8y 64z 64 . Chứng minh
x y z rằng xyz . 3
-------------------------------@Hết@----------------------------------- Trang 5 HƯỚNG DẪN GIẢI
I. Trắc nghiệm (4 điểm) Câu 1.
Trong hình vẽ dưới dây cho AOB 100 ; Ax là tiếp tuyến của O tại A . A x B 100° O Số đo xAB bằng A. 100 . B. 130 . C. 120 . D. 50 . Lời giải A x B 100° O 180 100
Có OA OB A
OB cân tại O OAB 40 2
xAB 90 40 130 .
2x y 3 Câu 2. Hệ phương trình có nghiệm là x y 3 A. 2 ;1 . B. 2 ;1 . C. 2 ; 1 . D. 2; 1 . Lời giải
2x y 3 3 x 6 x 2 . x y 3 x y 3 y 1 Câu 3.
Cho tam giác ABC vuông tại A , AB 3, BC 6 . Số đo của ACB bằng A. 90 . B. 45. C. 60 . D. 30 . Trang 6 Lời giải B 6 3 A C
Xét tam giác ABC vuông tại A có AB 1 sin ACB
ACB 30 . BC 2 Câu 4.
Căn bậc hai số học của 25 là A. 5 ;5 . B. 5 . C. 5 . D. 5 . Lời giải 25 5
Câu 5 . Hình nào dưới đây là đồ thị của hàm số 2 y x ? A. B. C. D. Lời giải
Với x 0 thì y 0 . Do đó 0;0 thuộc đồ thị hàm số 2 y x .
Với x 1 thì y 1. Do đó 1
;1 thuộc đồ thị hàm số 2 y x . Trang 7 3 Câu 6.
Cho tam giác ABC vuông tại A , AC 6 cm , tan B
. Độ dài cạnh BC bằng 4 A. 9 cm . B. 6 3 cm . C. 8 cm . D. 10 cm . Lời giải
Xét tam giác ABC vuông tại A AC Có: tan B
(định nghĩa tỉ số lượng giác) AB 3 Theo bài: tan B 4 AC 3 6 3 Suy ra:
AB 8cm BC 10cm AB 4 AB 4
Câu 7 . Biểu thức 3 x có điều kiện xác định là: A. x 3.
B. x 3.
C. x 3. D. x 3. Lời giải
Biểu thức 3 x có nghĩa khi 3 x 0 x 3 .
Câu 8 . Kết quả của phép tính 2 2 3 ( 3 ) bằng: A. 6 . B. 18 . C. 6 . D. 0 . Lời giải 2 2 3 ( 3 ) 3 3 6 Câu 9.
Hàm số y (m 5)x 2 (với m là tham số) đồng biến trên khi và chỉ khi: A. m 5 . B. m 5 . C. m 7 . D. m 7 . Lời giải
Hàm số y (m 5)x 2 (với m là tham số) đồng biến trên khi và chỉ khi
m 5 0 m 5 . Câu 10. Cho M
NP vuông tại M , đường cao MK . Hệ thức nào sau đây là sai? 1 1 1
A. MK.KP MN.MP . B. . 2 2 2 MK MN MP C. 2 MN N . P NK . D. 2
MK NK.KP . Lời giải
Áp dụng hệ thức lượng vào M
NP vuông tại M ta có: MK.NP MN.MP
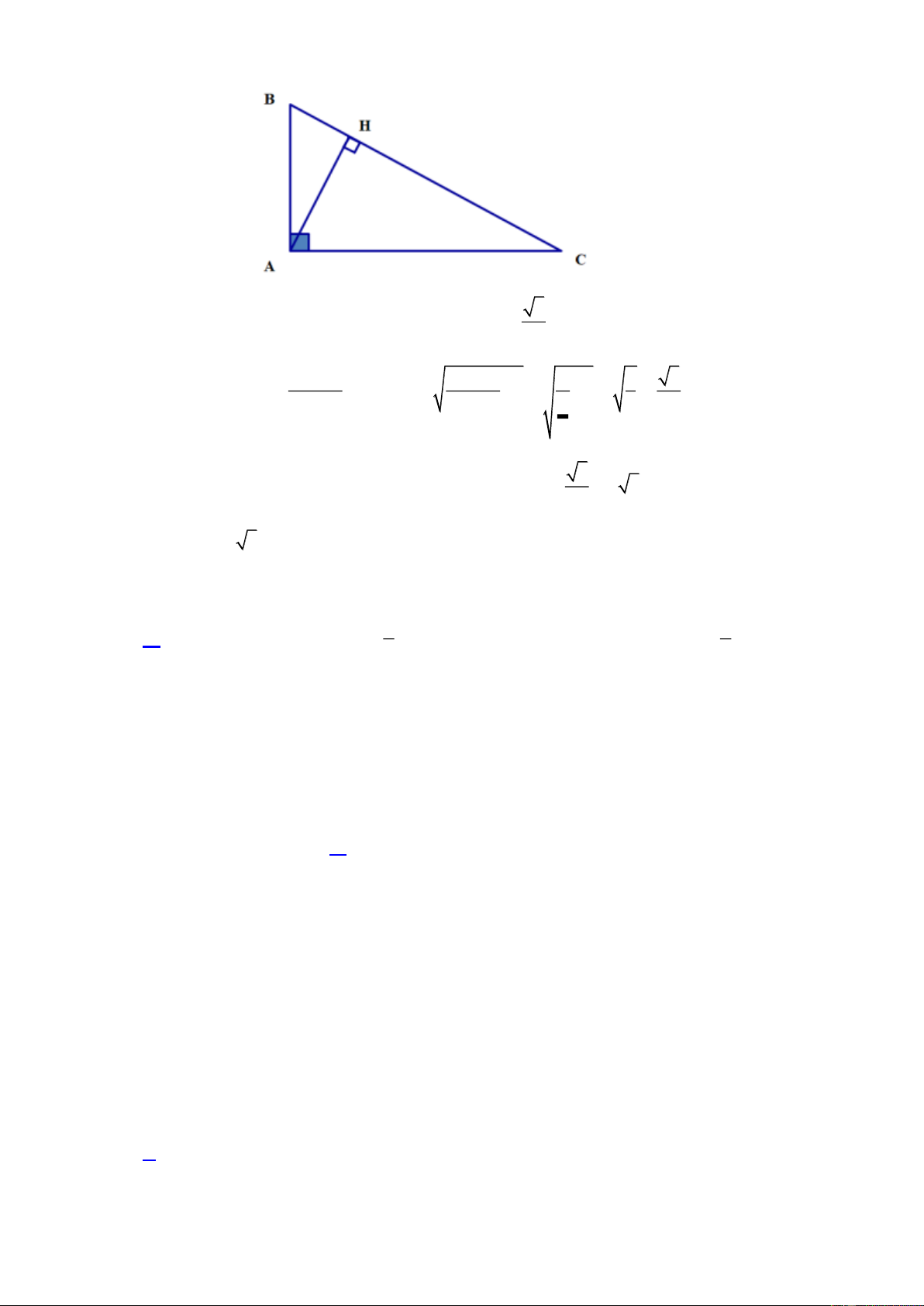
Câu 11 . Cho ABC
vuông tại A , đường cao AH 6c ,
m BH 4cm . Độ dài cạnh BC bằng: A. 10cm. B. 52cm . C. 9cm . D. 13cm . Lời giải Trang 8
Áp dụng hệ thức lượng vào ABC
vuông tại A ta có: 2
AH BH .CH 2 6 4.CH CH 9cm
Vậy BC CH BH 9 4 13cm 7 x
Câu 12 . Khi x 2
, biểu thức M có giá trị bằng: x 3 9 A. . B. 3 . C. 9 . D. 3 . 2 Lời giải 7 ( 2) 9 Khi x 2
, biểu thức M 3 2 3 1
Câu 13 . Hộp sữa có dạng hình trụ với đường kính đáy là 12 cm , chiều cao của hộp sữa là 18 cm . Thể
tích của hộp sữa bằng A. 3 648 cm B. 3 432 cm C. 3 216 cm D. 3 2592 cm Lời giải Ta có 2
V r h mà r 6 cm; h =18cm nên ta có 2 3
V 6 18 648 cm x y 3
Câu 14. Hệ phương trình
( với m là tham số) có nghiệm x ; y thỏa mãn x 2y khi 0 0
mx y 3 0 0 A. m 4 . B. m 2 . C. m 5 . D. m 3 . Lời giải x y 3 Hệ phương trình
( với m là tham số) có nghiệm x ; y thỏa mãn x 2y nên 0 0
mx y 3 0 0
thay x 2 y vào phương trình thứ nhất của hệ ta được: 0 0
3y 3 y 1 . Khi đó x 2 0 0 0
Thay x 2 và y 1 vào phương trình thứ hai của hệ ta được: 2m 1 3 2m 4 m 2 0 0
Câu 15. Cặp số nào sau đây là nghiệm của phương trình 2x y 1 A. 2; 2 . B. 1 ;3. C. 1 ; 3 . D. 2 ; 2 . Lời giải
Thay x 1; y 3 vào vế trái của phương trình 2x y 1 ta có 2. 1 3 2 3 1 Do đó 1 ; 3
là nghiệm của phương trình 2x y 1. Trang 9 3
Câu 16. Hệ số góc của đường thẳng y x là 2 3 A. -2 B. . C. -1 D. 2. 2 Lời giải 3 3 y
x x 2 2
Suy ra, hệ số góc của đường thẳng bằng -1
Câu 17 . Trong các hệ phương trình sau, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
xy 3x 1
x 2y 1 A. . B. .
y 2x 1 2
x 2y 1 x y 3 2 x 3y 1 C. . D. . 2x y 1
x 2y 1 Lời giải Chọn C Câu 18. Cho parabol 2
y x cắt đường thẳng y 3
x 4 tại hai điểm phân biệt có hoành độ
x x (x x ).Giá trị của biểu thức T 2x 3x bằng 1, 2 1 2 1 2 A. – 5. B. – 10. C. 10. D. 5. Lời giải
Phương trình hoành độ giao điểm của parabol và đường thẳng là 2 2 x 3
x 4 x 3x 4 0 (1)
Phương trình (1) có hai nghiệm x 4
; x 1 T 2.( 4 ) 3.1 5 1 2
Câu 19. Giao điểm của đồ thị hai hàm số y x 1 và y 2x 4 là A. N 1 ;1 . B. M 1;0. C. P 1 ;2. D. Q 3 ; 4 . Lời giải
Phương trình hoành độ giao điểm của đồ thị hai hàm số y x 1 và y 2x 4 là
x 1 2x 4 3x 3 x 1 Thay x 1
vào y x 1 ta có : y ( 1 ) 1 2
Vậy giao điểm của đồ thị hàm số y x 1 và y 2x 4 là P 1 ;2. 3
Câu 20. Cho tam giác ABC vuông tại A , đường cao AH . Cho biết CH 6cm và sin B . Độ dài 2
đường cao AH bằng A. 2cm . B. 4cm . C. 4 3cm . D. 2 3cm . Trang 10 Lời giải 3
Vì tam giác ABC vuông tại A nên sin B cos C . 2 1 1 1 1 3 Ta có : 2 1 tan C Tan C 1 1 2 2 Cos C Cos C 3 3 3 4 3
Tam giác AHC vuông tại H nên : AH HC.Tan C 6. 2 3cm 3
Vậy AH 2 3cm Câu 21. Cho hàm số 2
y ax (với a 0 là tham số). Điểm E(1; 2) Thuộc đồ thị hàm số khi 1 1 A. a 2 . B. a . C. a 2 . D. . 4 4 Lời giải
Vì điểm E(1; 2) thuộc đồ thị hàm số 2
y ax nên ta có : 2 2 . a 1 a Vậy a = 2
Câu 22. Đường thẳng nào dưới đây song song với đường thẳng y 2 x 1?
A. y 2x 1.
B. y 6 2x 1 .
C. y 2x 1.
D. y 1 2x . Lời giải a a
Đường thẳng d : y a b song song với d : y a x b khi: 1 2 2 1 1 1 2 2 b b 1 2
Trong 4 đáp án ta thấy có đáp B là thỏa mãn:
Đáp án B: y 6 2x
1 6 2x 1 2 x 5
2x y 7
Câu 23. Biết x ; y là nghiệm của hệ phương trình:
. Giá trị của biểu thức 2 2
x y bằng: o o x y 2 o o A. 8 . B. 5 . C. 10 . D. 7 . Lời giải Trang 11
2x y 7 3 x 9 x 3
Xét hệ phương trình: x y 2 x y 2 y 1
Giá trị của biểu thức: x y 2 2 2 2 3 1 9 1 8 . o o
Câu 24. Cho thể tích V của một hình nón có diện tích đáy S 2 6
cm và chiều cao h 3cm là A.V 3 9 cm . B. V 3 6 cm . C. V 3 3 cm . D. V 3 18 cm . Lời giải 1 1
Thể tích của hình nón là: V .S .h .6 .3 6 cm d 3 3 3
x 2y 3
Câu 25. Hệ phương trình
(với m là tham số) vô nghiệm khi
2x my 1 A. m 2 . B. m 4 . C. m 1. D. m 4 . Lời giải m 4 x 2 y 3 1 2 3 Hệ phương trình vô nghiệm khi 2 m 4.
2x my 1 2 m 1 m 3
Câu 26. Biểu thức 2 3 2x bằng A. 2x 3 . B. 2x 3 . C. 3 2x .
D. 2x 3 và 3 2x . Lời giải x2 3 2
3 2x 2x 3
Câu 27. Đường thẳng y 2x 3 đi qua điểm nào sau đây A. N 1 ;1 . B. Q 1 ; 1 . C. M 1; 1 .
D. P 1; 1 . Lời giải Xét với N 1 ;1 thay x 1
vào hàm số y 2x 3 ta được y 2. 1 3 5 1 nên đường
thẳng y 2x 3 không đi qua điểm N 1 ;1 . Xét Q 1 ; 1 thay x 1
vào hàm số y 2x 3 ta được y 2. 1 3 5 1 nên đường
thẳng y 2x 3 không đi qua điểm N 1 ;1 . a 2 a 6 4 Xét với M 1; 1 thay 1
vào hàm số y 2x 3 ta được 1 2b 2 b 2 y 2.1 3 1
1 nên đường thẳng y 2x 3 không đi qua điểm M 1; 1 . Trang 12
Xét với P 1;
1 thay x 1 vào hàm số y 2x 3 ta được y 2.1 3 1 nên đường thẳng
y 2x 3 đi qua điểm P 1; 1 . ax 3y 4
Câu 28. Cho hệ phương trình
( với a;b là tham số). Với giá trị nào của a;b thì hệ phương
x by 2
trình đã cho có nghiệm 1 ;2 ? a 2 a 2 a 2 a 2 A. . B. 1 . C. 1 . D. 1 . b 0 b b b 2 2 2 Lời giải
Vì hệ phương trình có nghiệm 1
;2 nên thay x 1
; y 2 vào hệ phương trình ta được a 2 a 6 4 1 . 1 2b 2 b 2
mx y 3
Câu 29. Cho hệ phương trình
(với m là tham số ).Số các giá trị nguyên của m để hệ 3
x my 4
phương trình đã cho có nghiệm duy nhất ;
x y thỏa mãn x 0, y 0 là A. 5 . B. 2 . C. 4 . D. 3 . Lời giải
mx y 3(1) (I) 3
x my 4( 2)
Từ (1) y mx 3 .Thay vào (2) ta được
3x m(mx 3) 4 2
3x m x 3m 4 2
x(m 3) 4 3 ( m *) Ta có 2
m 3 3 0 m
PT (*) luôn có nghiệm với mọi m
HPT (I) luôn có nghiệm với mọi m 4 3m Từ (*) x 2 m 3 2 4m 3m 4m 9 y 3 2 m 3 2 m 3 x 0 Để HPT (I) có nghiệm thì y 0 Trang 13 4 3m 0 2 m 3 4m 3 0 vì 2 (m 3 0 m ) 4m 9 4m 9 0 0 2 m 3 4 m 3 4 9 m 9 3 4 m 4
Mà m Z m 1 ;0;1; 2
Câu 30 . Trong mặt phẳng tọa độ Oxy,đồ thị hàm số y mx 2 (với m 0 là tham số) cắt các trục
Ox, Oy lần lượt tại ,
A B .Có bao nhiêu giá trị của m để diện tích tam giác OAB bằng 3 ? A. 3. B.1. C. 2 D. 0 Lời giải
Ta có y mx 2 ( m 0 )(d) 2 2
d Ox tại A A ; 0 OA m m
d Oy tại B B(0; 2) OB 2 Theo giả thiết S 3 OAB 1 O . A OB 3 2 1 2 . .2 3 2 m 2 m (t / m) 2 3 m 3 2
m 9(t / m) 3
Câu 31. Cho ba đường thẳng đôi một phân biệt y x 2d ; y 2x 1d ; y 2 m
1 x md 3 2 1
(với m là tham số). Giá trị của m để ba đường thẳng nói trên cùng đi qua một điểm là A. m 2 ;1 . B. m 1. C. m 2 . D. m 3 . Lời giải Gọi I ;
x y là giao điểm của d và d . Khi đó tọa độ điểm I là nghiệm của hệ phương trình 1 2 y x 2 x 1 . y 2x 1 y 3 Suy ra I 1;3 .
Để ba đường thẳng trên cùng đi qua một điểm thì I 1;3 thuộc đường thẳng d . 3 Trang 14 m
Thay x 1; y 3 vào y 2 m
1 x m ta được 2
3 m 1 m 2
m m 2 1 0 . m 2
Thử lại thấy m 1 thì d trùng với d nên loại m 1. 2 3 Vậy m 2 . 2 y 1 3 x 2
Câu 32. Hệ phương trình
có nghiệm x ; y thì x y bằng 0 0 1 0 0 3 y 1 2 x 2 A. 1. B. 2 . C. 2 . D. 1. Lời giải
(Điều kiện: x 2 ; y 1) 1 Đặt a
y b ( a 0;b 0 ) x và 1 2
2a b 3
6a 3b 9 a 1
Khi đó hệ phương trình trở thành .
a 3b 2
a 3b 2 b 1 1 1 1 x 1 Thay a
y b ta được x 2 . x và 1 2 y 2 y 1 1 Do đó x 1
; y 2 . Suy ra x y 1 2 1. 0 0 0 0
II. Tự luận (6 điểm) Câu 1. (1,0 điểm) x Rút gọn biểu thưc sau 1 1 1 A :
với x 0; x 4 x 2 x 2 4 x x 2 Lời giải 1 1 x 1 A :
với x 0; x 4 x 2 x 2 4 x x 2 x 2 x 2 x 1
x 2 x 2 x 2 x 2 x 2 x 2 : x 2 x 2 x 2 x 1 x 2 x 1 :
x 2 x 2 : x 2 x 2 x 2 x 2 x x 2 x 2 x .
x 2 x 2 . 1 Vậy A
x với x 0; x 4 . Trang 15 Câu 2. (1,5 điểm) Cho phương trình 2
x 2m
1 x m 3 0 (1) ( m là tham số).
1. Giải phương trình (1) khi m 0 .
2. Tìm giá trị của m để phương trình (1) có hai nghiệm đối nhau. Lời giải
1) Thay m 0 vào phương trình (1) ta có 2
x 2x 3 0 . (2)
Ta có a b c 1 2 3 0 nên phương trình (2) có 2 nghiệm phân biệt
x 1 hoặc x 3 1 2
Vậy với m 0, phương trình đã cho có hai nghiệm phân biệt là x 1 hoặc x 3 . 1 2 2
2) Ta có m m 2 2 ' 1 1.
3 m 2m 1 m 3 m 3m 4 2 3 7 m 0 với mọi m . 2 4
Phương trình (1) có hai nghiệm phân biệt với mọi m . Gọi x , x
là hai nghiệm của phương trình (1). 1 2
Áp dụng hệ thức Vi-ét ta có x x 2m 2 và x .x m 3 1 2 1 2
Để phương trình (1) có hai nghiệm đối nhau khi x x 0 1 2
2m 2 0 2m 2 m 1
Vậy với m 1 thì phương trình (1) có hai nghiệm đối nhau. Câu 3. (1,0 điểm)
Một phòng họp có 165 ghế ngồi được xếp thành các hàng, mỗi hàng có số ghế bằng nhau.
Trong một buổi họp có 208 người đến dự họp, do đó ban tổ chức đã kê thêm 1 hàng ghế và mỗi
hàng ghế phải nhiều hơn quy định 2 hàng ghế mới đủ chỗ ngồi. Hỏi lúc đầu mỗi phòng họp có
bao nhiêu hàng ghế, mỗi hàng ghế có bao nhiêu ghế? Trang 16 Lời giải
Gọi số hàng ghế ban đầu là x , (hàng ghế, x *) 165
Số ghế trên mỗi hàng khi dự định 165 người đến dự là: (ghế) x
Số hàng ghế sau khi kê thêm là: x 1(hàng ghế) 208
Số ghế trên mỗi hàng khi có 208 người đến dự là: x (ghế) 1
Vì khi có 208 người dự họp mỗi hàng phải kê thêm 2 ghế nên ta có phương trình: 208 165 2 2
2 208x 165x 165 2x 2x 2x 41x 165 0 x 1 x
x 15 (TM ) 2x
11 x 15 0 11 x (L) 2
Vậy số hàng ghế ban đầu là 15 hàng ghế.
Số ghế trên mỗi hàng là 11 ghế. Câu 4. (2,0 điểm)
Cho đường tròn tâm O đường kính BC . Trên đường tròn đã cho lấy điểm A cố định ( A khác
B và C ) và lấy điểm D thay đổi trên cung nhỏ AC ( D khác A và C ). Kẻ AH vuông góc
với BC ( H thuộc BC ). Hai đường thẳng BD và AH cắt nhau tại I .
1. Chứng minh tứ giác IHCD nội tiếp. 2. Chứng minh rằng 2
AB BI.B . D
3. Lấy điểm M trên đoạn thẳng BC sao cho BM AB . Chứng minh rằng tâm đường tròn
ngoại tiếp tam giác MID luôn nằm trên một đường thẳng cố định khi D thay đổi trên cung nhỏ AC . Lời giải
1) Xét (O) có BDC 90 (góc nội tiếp chắn nửa đường tròn) Trang 17
AHC 90 ( AH BC )
Xét tứ giác IHCD có IHC IDC 180
Mà 2 góc này ở vị trí đối nhau
Nên tứ giác IHCD nội tiếp.
2) Có BAI ACB (cùng phụ ABC ). Mà ACB BDA (góc nội tiếp cùng chắn AB )
BAI BDA Xét ABI và DBA có ABI chung BAI BDA Nên A BI ∽ D BA (g.g) AB BI 2
AB BI.B . D BD AB BM BI 3) +) Ta có 2 2
BM BA BM BA BI.BD nên
. Lại có MBI chung, ta suy ra BD BM B MI B
DM (c.g.c) suy ra BMI BDM (2 góc tương ứng). (3) 1
+) Gọi K là tâm đường tròn ngoại tiếp D
MI , ta có BDM IDM MKI (tính chất góc nội 2 tiếp). (4) 1
Từ (3) và (4) suy ra BMI
MKI MKI 2BMI 2 Xét tam giác cân M
KI có MKI 2KMI 180
hay 2BMI 2KMI 180 do đó
BMI KMI 90 BMK 90 suy ra KM BC .
Mà BC không đổi, BA BM không đổi, B cố định nên M cố định, suy ra K thuộc đường thẳng cố định. Câu 5. (0,5 điểm) Cho các số không âm ,
x y, z thỏa mãn điều kiện 2 2
x y 8x 8y 64z 64 . Chứng minh
x y z rằng xyz . 3 Lời giải Ta có: 2 2
x y 8x 8y 64z 0 2 2 2 2
x y 64z 8x 8y x y 64z 8z 8x 8y 8z 2 2
x y 72z 8.(x y z) (1) Lại có: 2 2
x y 2xy (theo BĐT Cauchy) (2) Trang 18
Vì x, y, z 0 nên 2xy 72z 2. 2x .
y 72z 24 xyz (theo BĐT Cauchy) (3)
x y z
Từ (1) (2) và (3) suy ra (x y z) 24 xyz xyz . 3 Trang 19